第3章 圆的基本知识 经典中考解答题 单元测试卷(含答案)
文档属性
| 名称 | 第3章 圆的基本知识 经典中考解答题 单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-28 11:30:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
《圆的基本性质》好题集锦(2019.10)
一、圆的有关线段和角
1.如图所示,已知△ABC内接于⊙O,AB=AC,∠BOC=120°,延长BO交⊙O于D点.
(1)试求∠BAD的度数;
(2)求证:△ABC为等边三角形.
2.如图,在⊙O中,直径CD⊥弦AB于点E,AM⊥BC于点M,交CD于点N,连接AD.
(1)求证:AD=AN;
(2)若AB=,ON=1,求⊙O的半径.
3.已知,在⊙O中,AB是⊙O的直径,点C.、P在AB的两侧,AC=AB,连接CP,BP.
(Ⅰ)如图①,若CP经过圆心,求∠P的大小;
(Ⅱ)如图②,点D是PB上一点,CD⊥PB,若CP⊥AB,求∠BCD的大小.
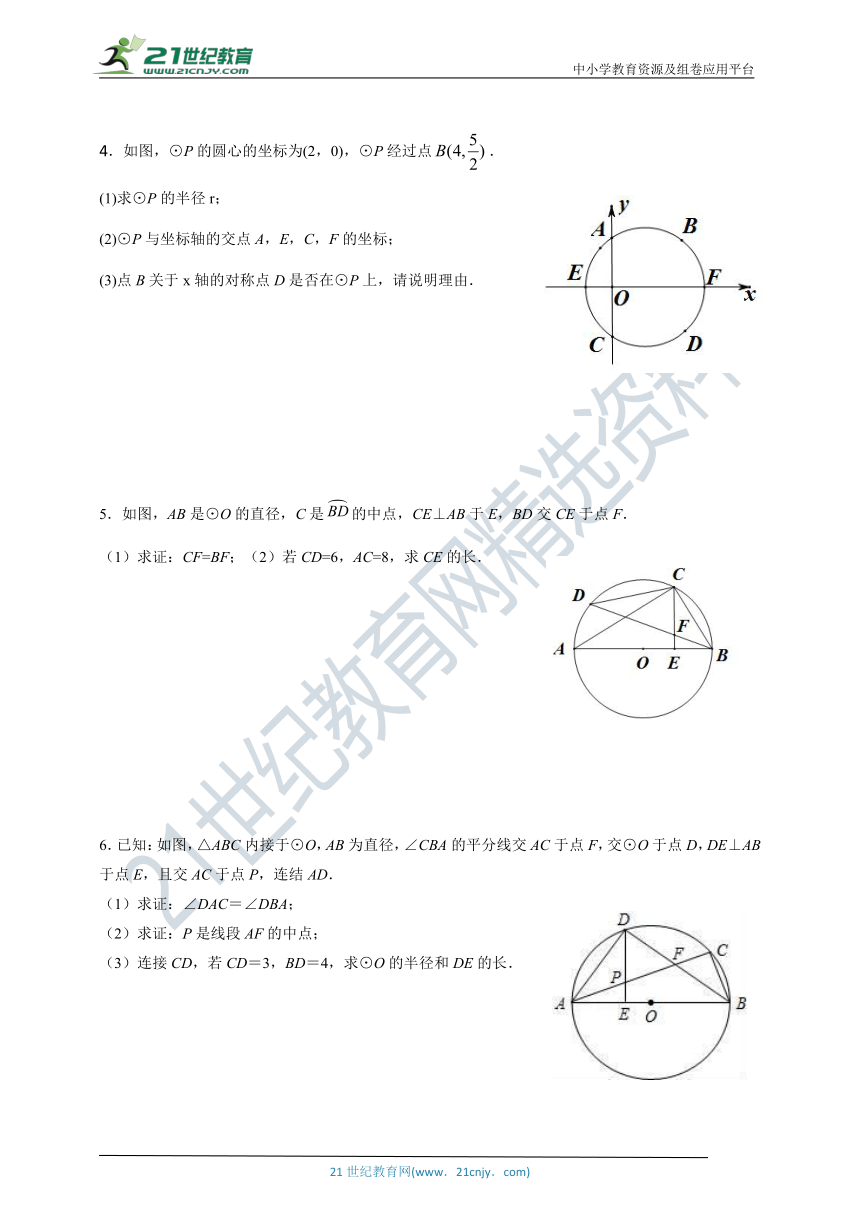
4.如图,⊙P的圆心的坐标为(2,0),⊙P经过点.
(1)求⊙P的半径r;
(2)⊙P与坐标轴的交点A,E,C,F的坐标;
(3)点B关于x轴的对称点D是否在⊙P上,请说明理由.
5.如图,AB是⊙O的直径,C是的中点,CE⊥AB于?E,BD交CE于点F.
(1)求证:CF=BF;(2)若CD=6,AC=8,求CE的长.
?
?
?
?
6.已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD=3,BD=4,求⊙O的半径和DE的长.
7.如图,四边形ABCD为圆内接四边形,对角线AC、BD交于点E,延长DA、CB交于点F,且∠CAD=60°,DC=DE. 求证:(1)AB=AF; (2)A为△BEF的外心(即△BEF外接圆的圆心).
二、圆与四边形
8.如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连结AE.
(1)求证:四边形AECD为平行四边形;(2)连结CO,求证:CO平分∠BCE.
9.如图,正方形ABCD的外接圆为⊙O,点P在劣弧 上(不与C点重合).
(1)求∠BPC的度数;(2)若⊙O的半径为8,求正方形ABCD的边长.
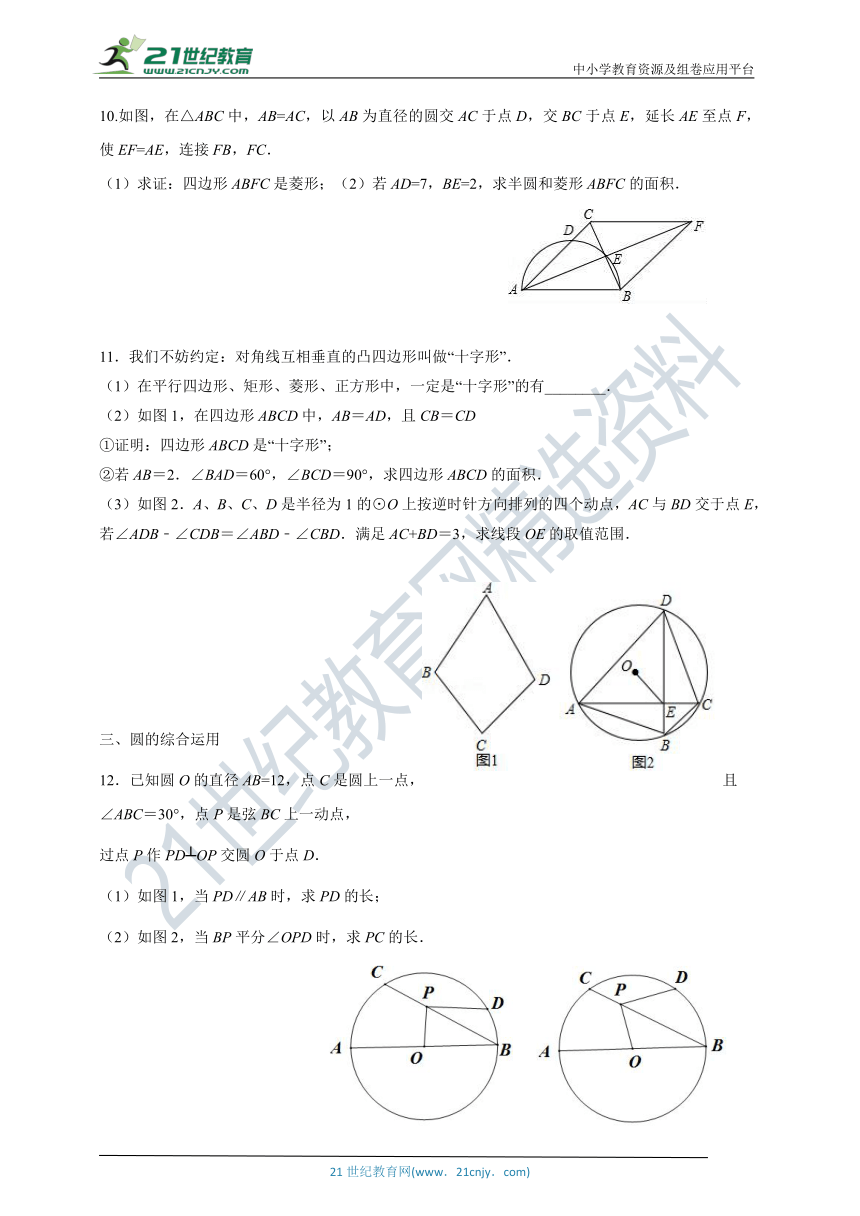
10.如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
11.我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)在平行四边形、矩形、菱形、正方形中,一定是“十字形”的有________.
(2)如图1,在四边形ABCD中,AB=AD,且CB=CD
①证明:四边形ABCD是“十字形”;
②若AB=2.∠BAD=60°,∠BCD=90°,求四边形ABCD的面积.
如图2.A、B、C、D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,若∠ADB﹣∠CDB=∠ABD﹣∠CBD.满足AC+BD=3,求线段OE的取值范围.
三、圆的综合运用
12.已知圆O的直径AB=12,点C是圆上一点,且∠ABC=30°,点P是弦BC上一动点,
过点P作PD┴OP交圆O于点D.
(1)如图1,当PD∥AB时,求PD的长;
(2)如图2,当BP平分∠OPD时,求PC的长.
?13.如图,点E为⊙O的直径AB上一个动点,点C、D在下半圆AB上(不含A、B两点),且∠CED=∠OED=60°,连OC、OD
(1)求证:∠C=∠D;
(2)若⊙O的半径为r,请直接写出CE+ED的变化范围(用含r的代数式表示).
14.如图,有两条公路?OM、ON?相交成?30°角,沿公路?OM?方向离?O?点?80?米处有一所学校?A.当 重型运输卡车?P?沿道路?ON?方向行驶时,在以?P?为圆心?50?米长为半径的圆形区域内都会受到卡车噪?声的影响,且卡车?P?与学校?A?的距离越近噪声影响越大.若已知重型运输卡车?P?沿道路?ON?方向行 驶的速度为?18?千米/时.
(1)求对学校?A?的噪声影响最大时卡车?P?与学校?A?的距离; 求卡车?P?沿道路?ON?方向行驶一次给学校?A?带来噪声影响的时间.
15.如图,以点P(﹣1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2,将△ABC绕点P旋转180°,得到△MCB.
(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
16.如图,△ABC内接于⊙O,AB=AC,CF垂直直径BD于点E,交边AB于点F.
(1)求证:∠BFC=∠ABC. (2)若⊙O的半径为5,CF=6,求AF长.
《圆的基本知识好题》参考答案
1.解:(1)∵BD是⊙O的直径,∴∠BAD=90°(直径所对的圆周角是直角).
(2)证明:∵∠BOC=120°,∴∠BAC=∠BOC=60°.又∵AB=AC,∴△ABC是等边三角形.
2.(1)证明:∵∠BAD与∠BCD是同弧所对的圆周角,
∴∠BAD=∠BCD,
∵AE⊥CD,AM⊥BC,∴∠AEN=∠AMC=90°,∵∠ANE=∠CNM,∴∠BAM=∠BCD,
∴∠BAM=∠BAD,,∴△ANE≌△ADE(ASA),∴AN=AD;
(2)解:∵AB=4,AE⊥CD,∴AE=2,又∵ON=1,∴设NE=x,则OE=x-1,NE=ED=x,OD=OE+ED=2x-1,解图,连接AO,则AO=OD=2x-1,
????????????
???????????????第2题解图
3.解:(1)∵AB是⊙O的直径,∴∠ACB=90°,∵AC=AB,∴∠ABC=30°,∴∠A=90°-∠ABC=60°,
∴∠P=∠A=60°;(Ⅱ) ∵AB是⊙O的直径,AC=AB, ∴∠A=60°,∴∠BPC=∠A=60°,
∵CD⊥PB∴∠PCD=90°-BPC=30°,∵CP⊥AB,AB是⊙O的直径,
∴BC=BP,∴∠P=∠BCP=60°,∴∠BCD=∠BCP-∠PCD=60°-30°=30°.
4..解:(1)过点B作x轴的垂线,交x轴于点G,连接BP.
则点G坐标为(4,0).
在Rt△PBG中,PG=4-2=2,BG=,斜边PB=∴⊙P的半径r=.
(2)点E坐标为(2-,0),点F坐标为(2+,0)∵点A坐标的y值=,∴点A坐标为(0,).点C坐标为(0,-).
(3)∵⊙P关于x轴对称,又∵B与D关于x轴对称,∴D在⊙P上.
5.证明:如图.∵AB是⊙O的直径,
∴∠ACB=90°,又∵CE⊥AB,∴∠CEB=90°.∴∠2=90°-∠ACE=∠A.
又∵C是弧BD的中点,∴∠1=∠A.∴∠1=∠2,∴?CF=BF.
此时,CE=
6.(1)证明:∵BD平分∠CBA,
∴∠CBD=∠DBA,
∵∠DAC与∠CBD都是弧CD所对的圆周角,
∴∠DAC=∠CBD,
∴∠DAC=∠DBA;
(2)证明:∵AB为直径, ∴∠ADB=90°,∵DE⊥AB于E,
∴∠DEB=90°,∴∠1+∠3=∠5+∠3=90°,∴∠1=∠5=∠2,
∴PD=PA,∵∠4+∠2=∠1+∠3=90°,且∠ADB=90°,∴∠3=∠4,
∴PD=PF,∴PA=PF,即P是线段AF的中点;
(3)解:连接CD, ∵∠CBD=∠DBA,∴CD=AD,∵CD=3,∴AD=3,
∵∠ADB=90°,AB=5,⊙O的半径为2.5,∵DE×AB=AD×BD,∴5DE=3×4,
∴DE=2.4.即DE的长为2.4.
7.(1)证明:∠ABF=∠ADC=120°﹣∠ACD=120°﹣∠DEC
=120°﹣(60°+∠ADE)=60°﹣∠ADE,
而∠F=60°﹣∠ACF,
因为∠ACF=∠ADE,
所以∠ABF=∠F,所以AB=AF.
(2)证明:四边形ABCD内接于圆,所以∠ABD=∠ACD,
又DE=DC,所以∠DCE=∠DEC=∠AEB,
所以∠ABD=∠AEB,
所以AB=AE.
∵AB=AF,
∴AB=AF=AE,即A是三角形BEF的外心.
8.(1)根据圆周角定理知∠E=∠B,
又∵∠B=∠D,∴∠E=∠D.
∵AD∥CE,∴∠D+∠DCE=180°,
∴∠E+∠DCE=180°,
∴AE∥DC,∴四边形AECD为平行四边形.
(2)如图,连结OE,OB,
由(1)得四边形AECD为平行四边形,
∴AD=EC.
又∵AD=BC,∴EC=BC.
∵OC=OC,OB=OE,
∴△OCE≌△OCB(SSS),
∴∠ECO=∠BCO,即OC平分∠BCE.
9.11.解:连接OB,OC,∵四边形ABCD为正方形,∴∠BOC=90°,∴∠BPC= ∠BOC=45°;
(2)解:过点O作OE⊥BC于点E, ∵OB=OC,∠BOC=90°,∴∠OBE=45°,∴OE=BE,∵OE2+BE2=OB2 , ∴BE= ?∴BC=2BE=
10.解析:(1)∵AB是直径,
∴∠AEB=90°,∴AE⊥BC,
∵AB=AC,∴BE=CE,
∵AE=EF,∴四边形ABFC是平行四边形,
∵AC=AB,∴四边形ABFC是菱形.
(2)设CD=x.连接BD.
∵AB是直径,∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
∴(7+x)2﹣72=42﹣x2,
解得x=1或﹣8(舍弃)
∴AC=8,BD=,
∴S菱形ABFC=.
∴S半圆=
11.15. (1)菱形,正方形
(2)解:①如图1,连接AC,BD
∵AB=AD,且CB=CD
∴AC是BD的垂直平分线,
∴AC⊥BD,
∴四边形ABCD是“十字形”
②如图,设AC与BD交于点O
∵AB=AD,AC⊥BD
∴∠BAO=∠BAD=30°
同理可证∠BCO=45°
在Rt△ABO中,OB=1
AO=AB×cos30°=
OB=OC=1
∴AC=AO+CO=1+, BD=2
∴ 四边形ABCD的面积=×AB×BD=×2×(1+)=1+
(3)解:如图2
∵∠ADB+∠CBD=∠ABD+∠CDB,∠CBD=∠CDB=∠CAB,
∴∠ADB+∠CAD=∠ABD+∠CAB,
∴180°﹣∠AED=180°﹣∠AEB,
∴∠AED=∠AEB=90°,
∴AC⊥BD,
过点O作OM⊥AC于M,ON⊥BD于N,连接OA,OD,
∴OA=OD=1,OM2=OA2﹣AM2 , ON2=OD2﹣DN2 , AM= AC,DN= BD,四边形OMEN是矩形,
∴ON=ME,OE2=OM2+ME2 ,
∴OE2=OM2+ON2=2﹣(AC2+BD2)
设AC=m,则BD=3﹣m,
∵⊙O的半径为1,AC+BD=3,
∴1≤m≤2,∴
12.连结OD??∵直径AB=12???∴OB=6??∵PD┴OP??????∴ ∠? DPO=90°?
∵PD∥AB??????∴∠?POB=90°????
又∵∠?ABC=30°?,OB=6∴OP=
∵在Rt△POD中,?由勾股定理得PD=
(2)过点O作OH┴BC,垂足为H?∵OH┴BC
??????∴∠?OHB=?OHP=90°∵∠?ABC=30°,OB=6∵在⊙O中,OH┴BC∴CH=BH=??∵BP平分∠OPD????∴ PH=3,
13.证明:(1)延长CE交⊙O于D′,连接OD′
∵∠CED=∠OED=60°,∴∠AEC=60°,OED′=60°,∴∠DEO=∠D′EO=60°,
由轴对称的性质可得∠D=∠D′,ED=ED′,∵OC=OD′,D′=∠C,∴∠C=∠D;
(2)∵∠D′EO=60°,∴∠C<60°,C=∠D′<60°,∴∠COD′>60°,∴CD′>OC=OD′,
∵CD′<OC+OD′,∵CE+ED=CE+ED′=CD′,∴r<CE+ED<2r.
14.解:(1)过点?A?作?AD⊥ON?于点?D,
∵∠NOM=30°,AO=80m,AD=40m,即对学校?A?的噪声影响最大时卡车?P?与学校?A?的距离为?40?米;
由图可知:以?50m?为半径画圆,分别交?ON?于?B,C?两点,AD⊥BC,BD=CD=BC,OA=80m,
∵在?Rt△AOD?中,∠AOB=30°,AD=?OA=?×80=40m,
在?Rt△ABD?中,AB=50,AD=40,由勾股定理得:BD=30m,?故BC=2×30=60?米,即重型运输卡车在经过?BC?时对学校产生影响.
∵重型运输卡车的速度为?18?千米/小时,即300?米/分钟,
∴重型运输卡车经过?BC?时需要?60÷300=0.2(分钟)=12(秒).
答:卡车?P?沿道路?ON?方向行驶一次给学校?A?带来噪声影响的时间为?12?秒.
15.(1)连接PA,如图1所示.∵PO⊥AD,∴AO=DO.∵AD=2,∴OA=.点P坐标为(﹣1,0),∴OP=1.∴PA==2.∴BP=CP=2.
∴B(﹣3,0),C(1,0).
(2)连接AP,延长AP交⊙P于点M,连接MB、MC.如图2所示,线段MB、MC即为所求作.
四边形ACMB是矩形.理由如下∵△MCB由△ABC绕点P旋转180°所得,
∴四边形ACMB是平行四边形.∵BC是⊙P的直径,∴∠CAB=90°.
∴平行四边形ACMB是矩形.过点M作MH⊥BC,垂足为H,如图2所示.
在△MHP和△AOP中,∵∠MHP=∠AOP,∠HPM=∠OPA,MP=AP,
∴△MHP≌△AOP.∴MH=OA=,PH=PO=1.∴OH=2.∴点M的坐标为(﹣2,).
(3)在旋转过程中∠MQG的大小不变.∵四边形ACMB是矩形,BMC=90°.EG⊥BO,
∴∠BGE=90°.∴∠BMC=∠BGE=90°.∵点Q是BE的中点,∴QM=QE=QB=QG.
∴点E、M、B、G在以点Q为圆心,QB为半径的圆上,如图3所示.
∴∠MQG=2∠MBG.∵∠COA=90°,OC=1,OA=,∴tan∠OCA=.
∴∠OCA=60°.∴∠MBC=∠BCA=60°.MQG=120°.
∴在旋转过程中∠MQG的大小不变,始终等于120°.
16.(1)证明:连结AD,
∵BD是⊙O的直径,∴∠BAD=90°,∵CF⊥BD,∴∠BEF =90°,∵∠ABD+∠ADB=90°,∠ABD+∠BFE=90°,∴∠BFC=∠ADB,∵AB=AC,∴∠ABC=∠ACB,∵∠ACB=∠ADB,∴∠BFC=∠ABC.
(2)解:连结CD,∵BD是⊙O的直径,∴∠BCD=90°,∵∠BFC=∠ABC,
∴BC=CF=6,∵BD=10,∴CD=8
在Rt△BCE中,BE=,CE=,,
,∴AF=AB-BF=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
