浙教版八年级上册第1章1.5.1 “边边边”判定方法 同步练习(含答案)
文档属性
| 名称 | 浙教版八年级上册第1章1.5.1 “边边边”判定方法 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 539.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-29 00:00:00 | ||
图片预览



文档简介
1.5 三角形全等的判定
第1课时 “边边边”判定方法
知识点1 三角形的稳定性
1.如图1-5-1所示,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法的根据是( )
A.两点之间,线段最短
B.两点确定一条直线
C.长方形的四个角都是直角
D.三角形的稳定性 图1-5-1
2.在生产和生活中:①用人字架来建筑房屋;②用窗钩来固定窗扇;③在栅栏门上斜钉着一根木条;④商店的推拉活动防盗门.其中用到三角形的稳定性的有( )
A.1种 B.2种 C.3种 D.4种
知识点2 利用“SSS”判定三角形全等
3.如图1-5-2,已知△ABC,则如图1-5-3所示的三角形中,与△ABC全等的是( )
图1-5-2 图1-5-3
4.如图1-5-4,已知CA=BD,利用“SSS”判定△ABD≌△DCA时,还需添加的条件
是__________.
图1-5-4 图1-5-5
5.如图1-5-5所示,在△ABC中,AB=AC,AD为BC边上的中线,则∠ADB的度数为________°.
6.如图1-5-6,C是AB的中点,AD=CE,CD=BE.求证:△ACD≌△CBE.
证明:∵C是AB的中点,
∴________=________.
在△ACD和△CBE中,∵
∴△ACD≌△CBE( ). 图1-5-6
7.已知:如图1-5-7,AB=DC,AE=DF,CE=BF.求证:∠B=∠C.
证明:∵CE=BF(________),
∴CE+EF=BF+EF,
即CF=BE.
在△ABE和△DCF中,
∵
∴△ABE≌△DCF(________),
∴∠B=∠C(____________________________). 图1-5-7
8.2018·贵州如图1-5-8,点A,D,C,B在同一条直线上,AC=BD,AE=BF,
CE=DF,求证:AE∥FB.
图1-5-8
知识点3 用尺规作已知角的平分线
9.2017·台州期末如图1-5-9,小敏做了一个角平分仪ABCD,其
中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB
和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE
就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可
得△ABC≌△ADC,这样就有∠QRE=∠PRE.说明△ABC≌△ADC的依据
是____________. 图1-5-9
10.已知∠α(如图1-5-10),用直尺和圆规作∠α的平分线.(不用写作法,保留作图痕迹)
图1-5-10
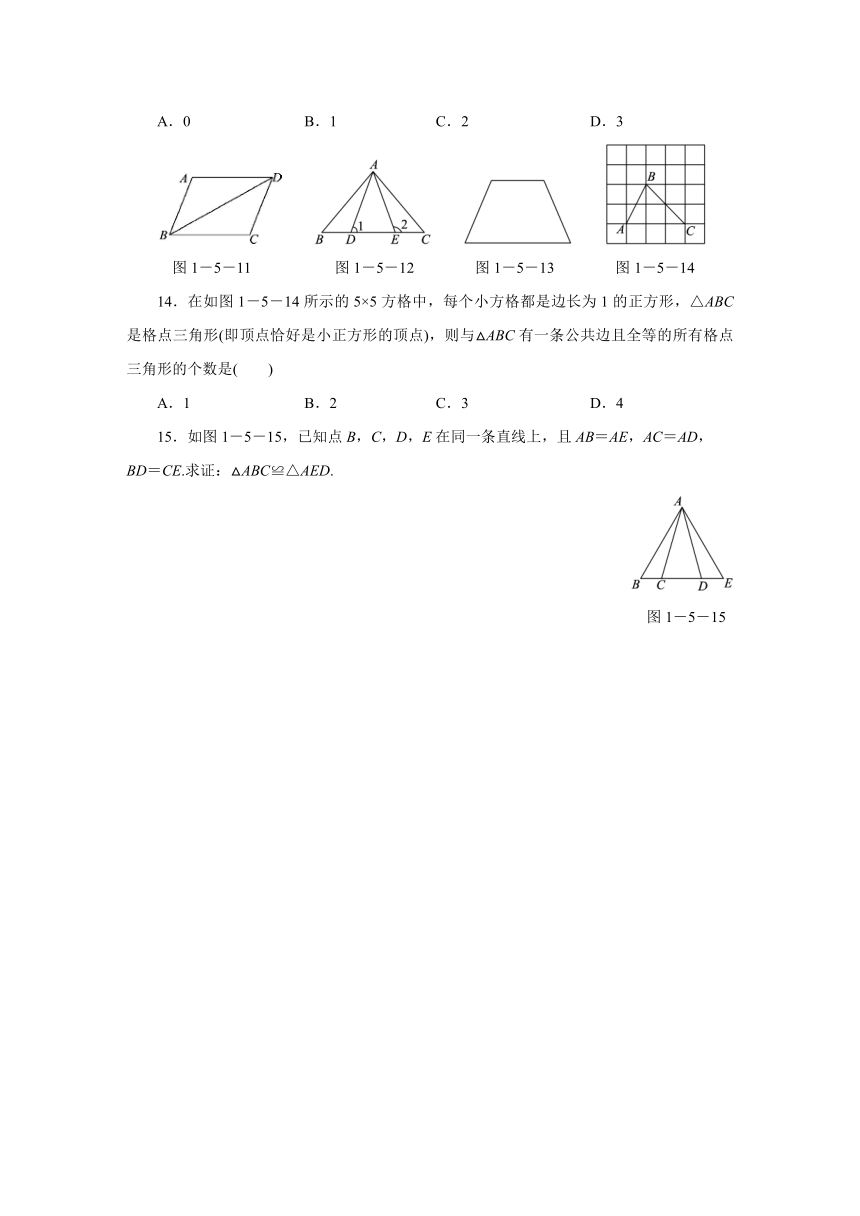
11.如图1-5-11,下列条件中,不能判定△ABD和△CBD全等的是( )
A.AB=BC,AD=CD B.沿BD对折后,点A,C重合
C.AB=DC,AD=BC D.AB=AD,BC=DC
12.如图1-5-12,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,下列结论错误的是( )
A.△ABE≌△ACD B.BD=CE C.∠ACE=30° D.∠1=70°
13.如图1-5-13,王师傅用4根木条钉成一个四边形木架,要使这个木架不变形,他至少需再钉上木条的根数是( )
A.0 B.1 C.2 D.3
图1-5-11 图1-5-12 图1-5-13 图1-5-14
14.在如图1-5-14所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是小正方形的顶点),则与△ABC有一条公共边且全等的所有格点三角形的个数是( )
A.1 B.2 C.3 D.4
15.如图1-5-15,已知点B,C,D,E在同一条直线上,且AB=AE,AC=AD,
BD=CE.求证:△ABC≌△AED.
图1-5-15
16.2018·桂林如图1-5-16,点A,D,C,F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:△ABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
图1-5-16
17.如图1-5-17,已知AD=BC,AC=BD,AC与BD相交于点O.
求证:∠DAO=∠CBO.
图1-5-17
教师详解详析
1.D [解析] 加上EF后,原不稳定的四边形ABCD中具有了稳定的△EAF,故这种做法的根据是三角形的稳定性.
2.C
3.C [解析] 三边对应相等的两个三角形全等,只有C选项的三角形与△ABC的各边对应相等.故选C.
4.AB=DC [解析] AD为公共边,第三组对应边为AB与DC.
5.90 [解析] 在△ABC中,
∵AD是BC边上的中线,∴BD=CD.
在△ABD和△ACD中,∵
∴△ABD≌△ACD(SSS),
∴∠ADB=∠ADC.
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°.
6.AC CB AC CB SSS
7.已知 DC 已知 AE 已知 CF SSS 全等三角形的对应角相等
8.证明:∵AC=BD,AE=BF,CE=DF,
∴△ACE≌△BDF,∴∠A=∠B,∴AE∥FB.
9.SSS
10.解:如图所示.
11.D
12.C [解析] ∵AB=AC,AE=AD,BE=CD,∴△ABE≌△ACD,故A项正确.
∵BD=BE-DE,CE=CD-DE,BE=CD,
∴BD=CE.
又∵AB=AC,AD=AE,∴△ABD≌△ACE,故B项正确.
∵∠2=∠B+∠BAE,∠2=110°,∠BAE=60°,∴∠B=50°.
∵△ABD≌△ACE,∴∠ACE=∠B=50°,故C项错误.
∵∠2+∠AEB=180°,∠2=110°,
∴∠AEB=70°.
∵△ABE≌△ACD,∴∠1=∠AEB=70°,故D项正确.
13.B [解析] 根据三角形的稳定性可得他至少需再钉上1根木条.故选B.
14.D
15.证明:∵BD=CE,
∴BD-CD=CE-CD,即BC=ED,
在△ABC和△AED中,∵
∴△ABC≌△AED(SSS).
16.解:(1)证明:∵AD=CF,
∴AD+CD=CF+CD,
即AC=DF.
在△ABC和△DEF中,∵
∴△ABC≌△DEF(SSS).
(2)在△ABC中,∵∠A=55°,∠B=88°,
∠A+∠B+∠BCA=180°,
∴∠BCA=180°―∠A―∠B=37°.
又∵△ABC≌△DEF,
∴∠F=∠BCA=37°.
17.证明:连结CD.
在△ACD和△BDC中,
∵∴△ACD≌△BDC(SSS),
∴∠DAO=∠CBO.
第1课时 “边边边”判定方法
知识点1 三角形的稳定性
1.如图1-5-1所示,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法的根据是( )
A.两点之间,线段最短
B.两点确定一条直线
C.长方形的四个角都是直角
D.三角形的稳定性 图1-5-1
2.在生产和生活中:①用人字架来建筑房屋;②用窗钩来固定窗扇;③在栅栏门上斜钉着一根木条;④商店的推拉活动防盗门.其中用到三角形的稳定性的有( )
A.1种 B.2种 C.3种 D.4种
知识点2 利用“SSS”判定三角形全等
3.如图1-5-2,已知△ABC,则如图1-5-3所示的三角形中,与△ABC全等的是( )
图1-5-2 图1-5-3
4.如图1-5-4,已知CA=BD,利用“SSS”判定△ABD≌△DCA时,还需添加的条件
是__________.
图1-5-4 图1-5-5
5.如图1-5-5所示,在△ABC中,AB=AC,AD为BC边上的中线,则∠ADB的度数为________°.
6.如图1-5-6,C是AB的中点,AD=CE,CD=BE.求证:△ACD≌△CBE.
证明:∵C是AB的中点,
∴________=________.
在△ACD和△CBE中,∵
∴△ACD≌△CBE( ). 图1-5-6
7.已知:如图1-5-7,AB=DC,AE=DF,CE=BF.求证:∠B=∠C.
证明:∵CE=BF(________),
∴CE+EF=BF+EF,
即CF=BE.
在△ABE和△DCF中,
∵
∴△ABE≌△DCF(________),
∴∠B=∠C(____________________________). 图1-5-7
8.2018·贵州如图1-5-8,点A,D,C,B在同一条直线上,AC=BD,AE=BF,
CE=DF,求证:AE∥FB.
图1-5-8
知识点3 用尺规作已知角的平分线
9.2017·台州期末如图1-5-9,小敏做了一个角平分仪ABCD,其
中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB
和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE
就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可
得△ABC≌△ADC,这样就有∠QRE=∠PRE.说明△ABC≌△ADC的依据
是____________. 图1-5-9
10.已知∠α(如图1-5-10),用直尺和圆规作∠α的平分线.(不用写作法,保留作图痕迹)
图1-5-10
11.如图1-5-11,下列条件中,不能判定△ABD和△CBD全等的是( )
A.AB=BC,AD=CD B.沿BD对折后,点A,C重合
C.AB=DC,AD=BC D.AB=AD,BC=DC
12.如图1-5-12,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,下列结论错误的是( )
A.△ABE≌△ACD B.BD=CE C.∠ACE=30° D.∠1=70°
13.如图1-5-13,王师傅用4根木条钉成一个四边形木架,要使这个木架不变形,他至少需再钉上木条的根数是( )
A.0 B.1 C.2 D.3
图1-5-11 图1-5-12 图1-5-13 图1-5-14
14.在如图1-5-14所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是小正方形的顶点),则与△ABC有一条公共边且全等的所有格点三角形的个数是( )
A.1 B.2 C.3 D.4
15.如图1-5-15,已知点B,C,D,E在同一条直线上,且AB=AE,AC=AD,
BD=CE.求证:△ABC≌△AED.
图1-5-15
16.2018·桂林如图1-5-16,点A,D,C,F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:△ABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
图1-5-16
17.如图1-5-17,已知AD=BC,AC=BD,AC与BD相交于点O.
求证:∠DAO=∠CBO.
图1-5-17
教师详解详析
1.D [解析] 加上EF后,原不稳定的四边形ABCD中具有了稳定的△EAF,故这种做法的根据是三角形的稳定性.
2.C
3.C [解析] 三边对应相等的两个三角形全等,只有C选项的三角形与△ABC的各边对应相等.故选C.
4.AB=DC [解析] AD为公共边,第三组对应边为AB与DC.
5.90 [解析] 在△ABC中,
∵AD是BC边上的中线,∴BD=CD.
在△ABD和△ACD中,∵
∴△ABD≌△ACD(SSS),
∴∠ADB=∠ADC.
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°.
6.AC CB AC CB SSS
7.已知 DC 已知 AE 已知 CF SSS 全等三角形的对应角相等
8.证明:∵AC=BD,AE=BF,CE=DF,
∴△ACE≌△BDF,∴∠A=∠B,∴AE∥FB.
9.SSS
10.解:如图所示.
11.D
12.C [解析] ∵AB=AC,AE=AD,BE=CD,∴△ABE≌△ACD,故A项正确.
∵BD=BE-DE,CE=CD-DE,BE=CD,
∴BD=CE.
又∵AB=AC,AD=AE,∴△ABD≌△ACE,故B项正确.
∵∠2=∠B+∠BAE,∠2=110°,∠BAE=60°,∴∠B=50°.
∵△ABD≌△ACE,∴∠ACE=∠B=50°,故C项错误.
∵∠2+∠AEB=180°,∠2=110°,
∴∠AEB=70°.
∵△ABE≌△ACD,∴∠1=∠AEB=70°,故D项正确.
13.B [解析] 根据三角形的稳定性可得他至少需再钉上1根木条.故选B.
14.D
15.证明:∵BD=CE,
∴BD-CD=CE-CD,即BC=ED,
在△ABC和△AED中,∵
∴△ABC≌△AED(SSS).
16.解:(1)证明:∵AD=CF,
∴AD+CD=CF+CD,
即AC=DF.
在△ABC和△DEF中,∵
∴△ABC≌△DEF(SSS).
(2)在△ABC中,∵∠A=55°,∠B=88°,
∠A+∠B+∠BCA=180°,
∴∠BCA=180°―∠A―∠B=37°.
又∵△ABC≌△DEF,
∴∠F=∠BCA=37°.
17.证明:连结CD.
在△ACD和△BDC中,
∵∴△ACD≌△BDC(SSS),
∴∠DAO=∠CBO.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
