浙教版八年级上册第1章1.5.4 “角角边”判定方法与角平分线的性质 同步练习(含答案)
文档属性
| 名称 | 浙教版八年级上册第1章1.5.4 “角角边”判定方法与角平分线的性质 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 719.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-29 00:00:00 | ||
图片预览



文档简介
1.5第4课时 “角角边”判定方法与角平分线的性质
知识点1 利用“AAS”判定三角形全等
1.如图1-5-48所示,AB与CD相交于点O,∠A=∠B,
CO=DO.又因为________=________,所以△AOC≌△BOD,
其依据是________________. 图1-5-48
2.如图1-5-49,E,A,C三点共线,AB∥CD,∠B=∠E,AC=CD.
求证:BC=ED.
图1-5-49
3.如图1-5-50,已知AD∥CE,∠1=∠2.D为线段BE的中点,证明:△ABD≌△CDE.
图1-5-50
知识点2 全等三角形判定与性质的结合
4.如图1-5-51所示,∠ACB′=∠A′C′B,∠B=∠B′,AB=A′B′,点B,C′,C,B′在同一条直线上.若∠A=68°,则∠A′=________°. 图1-5-51
5.如图1-5-52,四边形ABCD是一防洪堤坝的横截面,AE⊥CD,BF⊥CD,垂足分别为E,F,且AE=BF,∠D=∠C,则AD与BC是否相等?说明你的理由.
解:AD=BC.理由:在△ADE和△BCF中,
∵
∴△ADE≌△BCF(________),
∴AD=BC(____________________________). 图1-5-52
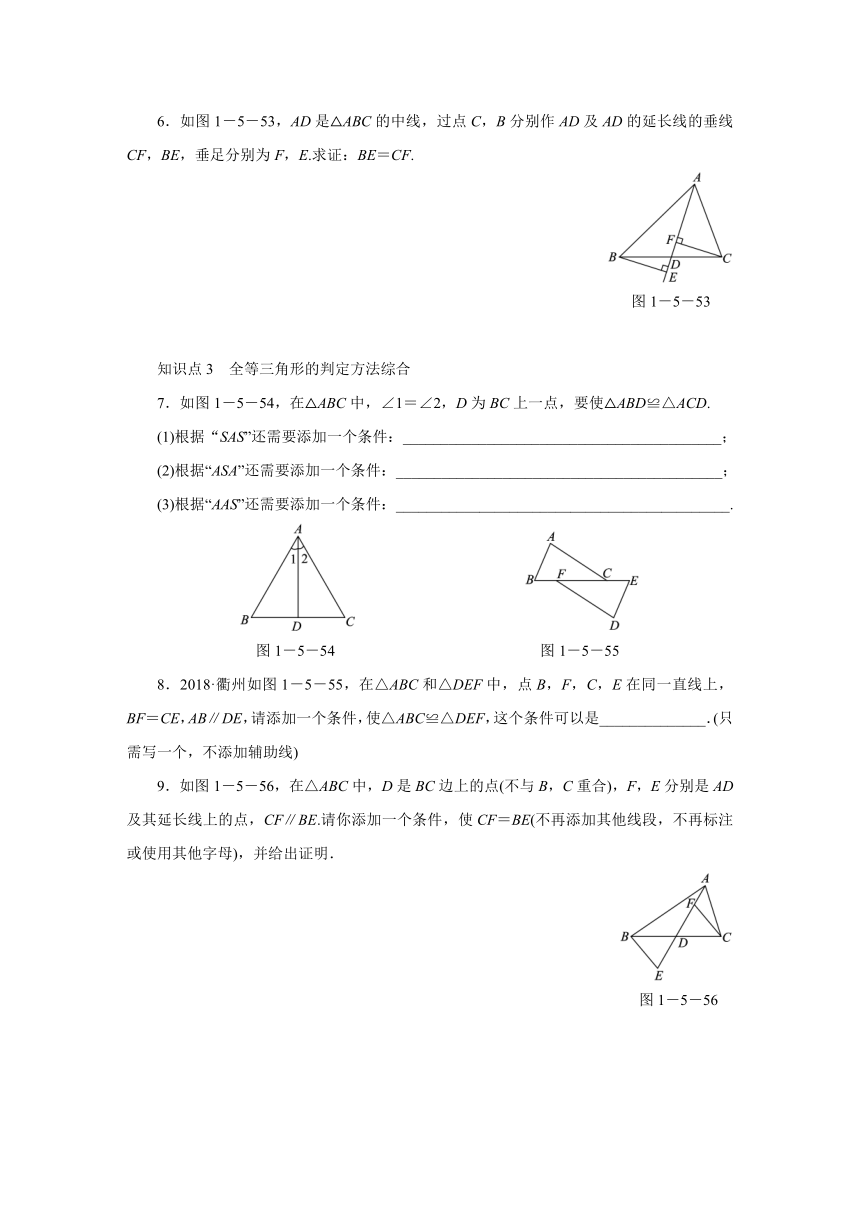
6.如图1-5-53,AD是△ABC的中线,过点C,B分别作AD及AD的延长线的垂线CF,BE,垂足分别为F,E.求证:BE=CF.
图1-5-53
知识点3 全等三角形的判定方法综合
7.如图1-5-54,在△ABC中,∠1=∠2,D为BC上一点,要使△ABD≌△ACD.
(1)根据“SAS”还需要添加一个条件:__________________________________________;
(2)根据“ASA”还需要添加一个条件:___________________________________________;
(3)根据“AAS”还需要添加一个条件:____________________________________________.
图1-5-54 图1-5-55
8.2018·衢州如图1-5-55,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个条件可以是______________.(只需写一个,不添加辅助线)
9.如图1-5-56,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,使CF=BE(不再添加其他线段,不再标注或使用其他字母),并给出证明.
图1-5-56
知识点4 角平分线的性质
10.如图1-5-57,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D.若
PD=6,则点P到OB的距离为( )
A.6 B.5 C.4 D.3
图1-5-57 图1-5-58
11.如图1-5-58,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论中错误的是( )
A.PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD
12.如图1-5-59所示,OC平分∠AOB,OA=OB,P为OC上一点,PE⊥AC,PF⊥BC,垂足分别为E,F.求证:PE=PF.
图1-5-59
13.如图1-5-60所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
图1-5-60 图1-5-61
14.如图1-5-61,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F.若
S△ABC=7,DE=2,AB=4,则AC=__________.
15.2017·台州期末如图1-5-62,在四边形ABCD中,已知BD平分∠ABC,∠BAD+∠C=180°.求证:AD=CD.
图1-5-62
16.如图1-5-63,AE⊥AB且AE=AB,BC⊥CD且BC=CD,EF⊥FH,BG⊥FH,DH⊥FH,垂足分别为F,G,H,点A,C均在FH上,请按照图中所标注的数据,计算图中实线所围成的图形的面积S.
图1-5-63
教师详解详析
1.∠AOC ∠BOD AAS
2.证明:∵AB∥CD,∴∠BAC=∠ECD.
在△ABC与△CED中,∵
∴△ABC≌△CED(AAS),
∴BC=ED.
3.证明:∵AD∥CE,
∴∠ADB=∠CED.
∵D是BE的中点,
∴BD=DE.
在△ABD和△CDE中,
∵
∴△ABD≌△CDE(AAS).
4.68
5.∠C 已知 BFC 垂直的定义 BF 已知 AAS 全等三角形的对应边相等
6.[解析] 欲证明BE=CF,可证明△BED≌△CFD.由中线的定义及垂直的定义和对顶角的性质可以解决问题.
证明:∵AD是△ABC的中线,
∴BD=CD(中线的定义).
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°(垂直的定义).
在△BED和△CFD中,
∵
∴△BED≌△CFD(AAS),∴BE=CF.
7.(1)AB=AC
(2)∠BDA=∠CDA或AD⊥BC
(3)∠B=∠C
[解析] 注意公共边AD的使用.因为∠1是AB与AD的夹角,∠2是AC与AD的夹角,所以(1)应填AB=AC;因为AD是∠1与∠BDA的夹边,也是∠2与∠CDA的夹边,所以(2)应填∠BDA=∠CDA或AD⊥BC;因为AD在△ABD中的对角是∠B,在△ACD中的对角是∠C,所以(3)应填∠B=∠C.
8.(答案不唯一)∠A=∠D
9.解:答案不唯一,如添加的条件是BD=CD.
证明:∵CF∥BE(已知),
∴∠EBD=∠FCD(两直线平行,内错角相等).
在△BDE和△CDF中,
∵
∴△BDE≌△CDF(ASA),
∴CF=BE(全等三角形的对应边相等).
10.A
11.B [解析] ∵OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,∴PC=PD,故A正确;
在△OCP与△ODP中,
∵
∴△OCP≌△ODP,
∴∠CPO=∠DPO,OC=OD,故C,D正确;
不能得出∠CPD=∠DOP,故B错误.
故选B.
12.[解析] 由OC平分∠AOB,OA=OB,OC为公共边,可得△AOC≌△BOC,从而可得∠ACO=∠BCO.又∵PE⊥AC,PF⊥BC,∴PE=PF.
证明:∵OC平分∠AOB,∴∠AOC=∠BOC.在△AOC和△BOC中,
∵
∴△AOC≌△BOC,∴∠ACO=∠BCO.
∴CO平分∠ACB.
又∵P为OC上一点,PE⊥AC,PF⊥BC,
∴PE=PF.
13.C [解析] ∵∠E=∠F=90°,∠B=∠C,
∴∠EAB=∠FAC.
又∵AE=AF,∴△AEB≌△AFC,∴AB=AC.在△ACN和△ABM中,
∵
∴△ACN≌△ABM(ASA),故④正确.
∵∠EAB=∠FAC,
∴∠EAB-∠CAB=∠FAC-∠CAB,
即∠EAM=∠FAN,故③正确.
在△EAM和△FAN中,∵
∴△EAM≌△FAN(ASA),∴EM=FN,故①正确.
由已知条件不能得出CD=DN,故正确的结论有3个.
14.3 [解析] ∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF=2.
∵AB=4,∴S△ABD=×4×2=4.
∵S△ABC=7,∴S△ACD=3,∴AC==3.
15.证明:如图,过点D分别作DM⊥BA交BA的延长线于点M,DN⊥BC于点N,因此∠AMD=∠CND=90°.
∵BD平分∠ABC,∴DM=DN.
∵∠BAD+∠C=180°,∠BAD+∠DAM=180°,∴∠C=∠DAM.
在△AMD与△CND中,
∵
∴△AMD≌△CND(AAS),∴AD=CD.
16.解:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH,
∴∠EAB=∠EFA=∠AGB=90°,
∴∠EAF+∠BAG=90°,∠ABG+∠BAG=90°,
∴∠EAF=∠ABG.
又∵AE=BA,∠EFA=∠AGB,
∴△EFA≌△AGB,
∴AF=BG=3,EF=AG=6.
同理可得△BGC≌△CHD,
得GC=HD=4,BG=CH=3.
故FH=AF+AG+GC+CH=3+6+4+3=16,
故S=×(6+4)×16-2××3×4-2××6×3=50.
知识点1 利用“AAS”判定三角形全等
1.如图1-5-48所示,AB与CD相交于点O,∠A=∠B,
CO=DO.又因为________=________,所以△AOC≌△BOD,
其依据是________________. 图1-5-48
2.如图1-5-49,E,A,C三点共线,AB∥CD,∠B=∠E,AC=CD.
求证:BC=ED.
图1-5-49
3.如图1-5-50,已知AD∥CE,∠1=∠2.D为线段BE的中点,证明:△ABD≌△CDE.
图1-5-50
知识点2 全等三角形判定与性质的结合
4.如图1-5-51所示,∠ACB′=∠A′C′B,∠B=∠B′,AB=A′B′,点B,C′,C,B′在同一条直线上.若∠A=68°,则∠A′=________°. 图1-5-51
5.如图1-5-52,四边形ABCD是一防洪堤坝的横截面,AE⊥CD,BF⊥CD,垂足分别为E,F,且AE=BF,∠D=∠C,则AD与BC是否相等?说明你的理由.
解:AD=BC.理由:在△ADE和△BCF中,
∵
∴△ADE≌△BCF(________),
∴AD=BC(____________________________). 图1-5-52
6.如图1-5-53,AD是△ABC的中线,过点C,B分别作AD及AD的延长线的垂线CF,BE,垂足分别为F,E.求证:BE=CF.
图1-5-53
知识点3 全等三角形的判定方法综合
7.如图1-5-54,在△ABC中,∠1=∠2,D为BC上一点,要使△ABD≌△ACD.
(1)根据“SAS”还需要添加一个条件:__________________________________________;
(2)根据“ASA”还需要添加一个条件:___________________________________________;
(3)根据“AAS”还需要添加一个条件:____________________________________________.
图1-5-54 图1-5-55
8.2018·衢州如图1-5-55,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个条件可以是______________.(只需写一个,不添加辅助线)
9.如图1-5-56,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,使CF=BE(不再添加其他线段,不再标注或使用其他字母),并给出证明.
图1-5-56
知识点4 角平分线的性质
10.如图1-5-57,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D.若
PD=6,则点P到OB的距离为( )
A.6 B.5 C.4 D.3
图1-5-57 图1-5-58
11.如图1-5-58,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论中错误的是( )
A.PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD
12.如图1-5-59所示,OC平分∠AOB,OA=OB,P为OC上一点,PE⊥AC,PF⊥BC,垂足分别为E,F.求证:PE=PF.
图1-5-59
13.如图1-5-60所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
图1-5-60 图1-5-61
14.如图1-5-61,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F.若
S△ABC=7,DE=2,AB=4,则AC=__________.
15.2017·台州期末如图1-5-62,在四边形ABCD中,已知BD平分∠ABC,∠BAD+∠C=180°.求证:AD=CD.
图1-5-62
16.如图1-5-63,AE⊥AB且AE=AB,BC⊥CD且BC=CD,EF⊥FH,BG⊥FH,DH⊥FH,垂足分别为F,G,H,点A,C均在FH上,请按照图中所标注的数据,计算图中实线所围成的图形的面积S.
图1-5-63
教师详解详析
1.∠AOC ∠BOD AAS
2.证明:∵AB∥CD,∴∠BAC=∠ECD.
在△ABC与△CED中,∵
∴△ABC≌△CED(AAS),
∴BC=ED.
3.证明:∵AD∥CE,
∴∠ADB=∠CED.
∵D是BE的中点,
∴BD=DE.
在△ABD和△CDE中,
∵
∴△ABD≌△CDE(AAS).
4.68
5.∠C 已知 BFC 垂直的定义 BF 已知 AAS 全等三角形的对应边相等
6.[解析] 欲证明BE=CF,可证明△BED≌△CFD.由中线的定义及垂直的定义和对顶角的性质可以解决问题.
证明:∵AD是△ABC的中线,
∴BD=CD(中线的定义).
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°(垂直的定义).
在△BED和△CFD中,
∵
∴△BED≌△CFD(AAS),∴BE=CF.
7.(1)AB=AC
(2)∠BDA=∠CDA或AD⊥BC
(3)∠B=∠C
[解析] 注意公共边AD的使用.因为∠1是AB与AD的夹角,∠2是AC与AD的夹角,所以(1)应填AB=AC;因为AD是∠1与∠BDA的夹边,也是∠2与∠CDA的夹边,所以(2)应填∠BDA=∠CDA或AD⊥BC;因为AD在△ABD中的对角是∠B,在△ACD中的对角是∠C,所以(3)应填∠B=∠C.
8.(答案不唯一)∠A=∠D
9.解:答案不唯一,如添加的条件是BD=CD.
证明:∵CF∥BE(已知),
∴∠EBD=∠FCD(两直线平行,内错角相等).
在△BDE和△CDF中,
∵
∴△BDE≌△CDF(ASA),
∴CF=BE(全等三角形的对应边相等).
10.A
11.B [解析] ∵OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,∴PC=PD,故A正确;
在△OCP与△ODP中,
∵
∴△OCP≌△ODP,
∴∠CPO=∠DPO,OC=OD,故C,D正确;
不能得出∠CPD=∠DOP,故B错误.
故选B.
12.[解析] 由OC平分∠AOB,OA=OB,OC为公共边,可得△AOC≌△BOC,从而可得∠ACO=∠BCO.又∵PE⊥AC,PF⊥BC,∴PE=PF.
证明:∵OC平分∠AOB,∴∠AOC=∠BOC.在△AOC和△BOC中,
∵
∴△AOC≌△BOC,∴∠ACO=∠BCO.
∴CO平分∠ACB.
又∵P为OC上一点,PE⊥AC,PF⊥BC,
∴PE=PF.
13.C [解析] ∵∠E=∠F=90°,∠B=∠C,
∴∠EAB=∠FAC.
又∵AE=AF,∴△AEB≌△AFC,∴AB=AC.在△ACN和△ABM中,
∵
∴△ACN≌△ABM(ASA),故④正确.
∵∠EAB=∠FAC,
∴∠EAB-∠CAB=∠FAC-∠CAB,
即∠EAM=∠FAN,故③正确.
在△EAM和△FAN中,∵
∴△EAM≌△FAN(ASA),∴EM=FN,故①正确.
由已知条件不能得出CD=DN,故正确的结论有3个.
14.3 [解析] ∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF=2.
∵AB=4,∴S△ABD=×4×2=4.
∵S△ABC=7,∴S△ACD=3,∴AC==3.
15.证明:如图,过点D分别作DM⊥BA交BA的延长线于点M,DN⊥BC于点N,因此∠AMD=∠CND=90°.
∵BD平分∠ABC,∴DM=DN.
∵∠BAD+∠C=180°,∠BAD+∠DAM=180°,∴∠C=∠DAM.
在△AMD与△CND中,
∵
∴△AMD≌△CND(AAS),∴AD=CD.
16.解:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH,
∴∠EAB=∠EFA=∠AGB=90°,
∴∠EAF+∠BAG=90°,∠ABG+∠BAG=90°,
∴∠EAF=∠ABG.
又∵AE=BA,∠EFA=∠AGB,
∴△EFA≌△AGB,
∴AF=BG=3,EF=AG=6.
同理可得△BGC≌△CHD,
得GC=HD=4,BG=CH=3.
故FH=AF+AG+GC+CH=3+6+4+3=16,
故S=×(6+4)×16-2××3×4-2××6×3=50.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
