4.1 比例线段-黄金分割 同步练习(解析版)
文档属性
| 名称 | 4.1 比例线段-黄金分割 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-29 00:00:00 | ||
图片预览




文档简介
初中数学浙教版九年级上册4.1 比例线段-黄金分割 同步训练
一、基础巩固
1.已知,C是线段AB的黄金分割点,AC<BC,若AB=2,则BC=(?? )
A.?3﹣ ?????????????????????B.?( +1)?????????????????????C.?﹣1?????????????????????D.?( ﹣1)
2.点C是线段AB的黄金分割点,且AB=6cm,则BC的长为(??? )cm
A.?????????????????B.?????????????????C.?或 ????????????????D.?或
3.主持人站在舞台的黄金分割点处最自然得体,如果舞台AB长为20米,一个主持人现站在舞台AB的黄金分割点点C处,则下列结论一定正确的是(?? )21教育网
①AB:AC=AC:BC;②AC≈6.18米;③AC=10( )米;④BC=10(3? )米或10( ?1)米.
A.?①②③④??????????????????????????????????B.?①②③??????????????????????????????????C.?①③??????????????????????????????????D.?④
4.在长度为1的线段上找到两个黄金分割点P,Q,则PQ=(??? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
5.已知 为线段 的黄金分割点,且 ,则(??? ).
A.?????????????B.??????????????C.?????????????D.?
6.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20cm,则它的宽约为(?? ) 21·cn·jy·com
A.?12.36 cm???????????????????????????B.?13.6 cm???????????????????????????C.?32.36 cm???????????????????????????D.?7.64 cm
7.若a:b=3:2,且b是a、c的比例中项,则b:c等于(?? )
A.?4:3????????????????????????????????????B.?3:4????????????????????????????????????C.?3:2????????????????????????????????????D.?2:3
8.已知线段a=4,b=9,线段x是a,b的比例中项,则x等于(?? )
A.?6???????????????????????????????????????B.?6或﹣6???????????????????????????????????????C.?﹣6???????????????????????????????????????D.?36
9.若 ,请再写出一条线段的长,使它与a、b这三条线段中的一条是另外两条的比例中项,则这条线段长为________. 2-1-c-n-j-y
10.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么AP的长度为________cm. 【
11.电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB长为20m,试计算主持人应走到离A点至少________m处.(结果精确到0.1m)
12.已知线段a=0.3m,b=60cm,c=12dm.
(1)求线段a与线段b的比.
(2)如果线段a、b、c、d成比例,求线段d的长.
(3)b是a和c的比例中项吗?为什么?
二、提高特训
13.点C为线段AB的黄金分割点,且AC>BC,下列说法正确的有(?? )
①AC= AB,②AC= AB,③AB:AC=AC:BC,④AC≈0.618AB
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
14.“黄金分割”是一条举世公认的美学定律. 例如在摄影中,人们常依据黄金分割进行构图,使画面整体和谐. 目前,照相机和手机自带的九宫格就是黄金分割的简化版. 要拍摄草坪上的小狗,按照黄金分割的原则,应该使小狗置于画面中的位置(?? )21*cnjy*com
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
15.如果一个矩形的宽(即短边)与长(即长边)之比是 ,那么这个矩形称为黄金矩形.如图,矩形ABCD是黄金矩形,点E,F,G,H分别为线段AD,BC,AB,EF的中点,则图中黄金矩形的个数是(? ?)
A.?5个???????????????????????????????????????B.?4个???????????????????????????????????????C.?3个???????????????????????????????????????D.?2个
16.如图,在五角星中,AD=BC,且C、D两点都是AB的黄金分割点,CD=1,则AB的长是________.
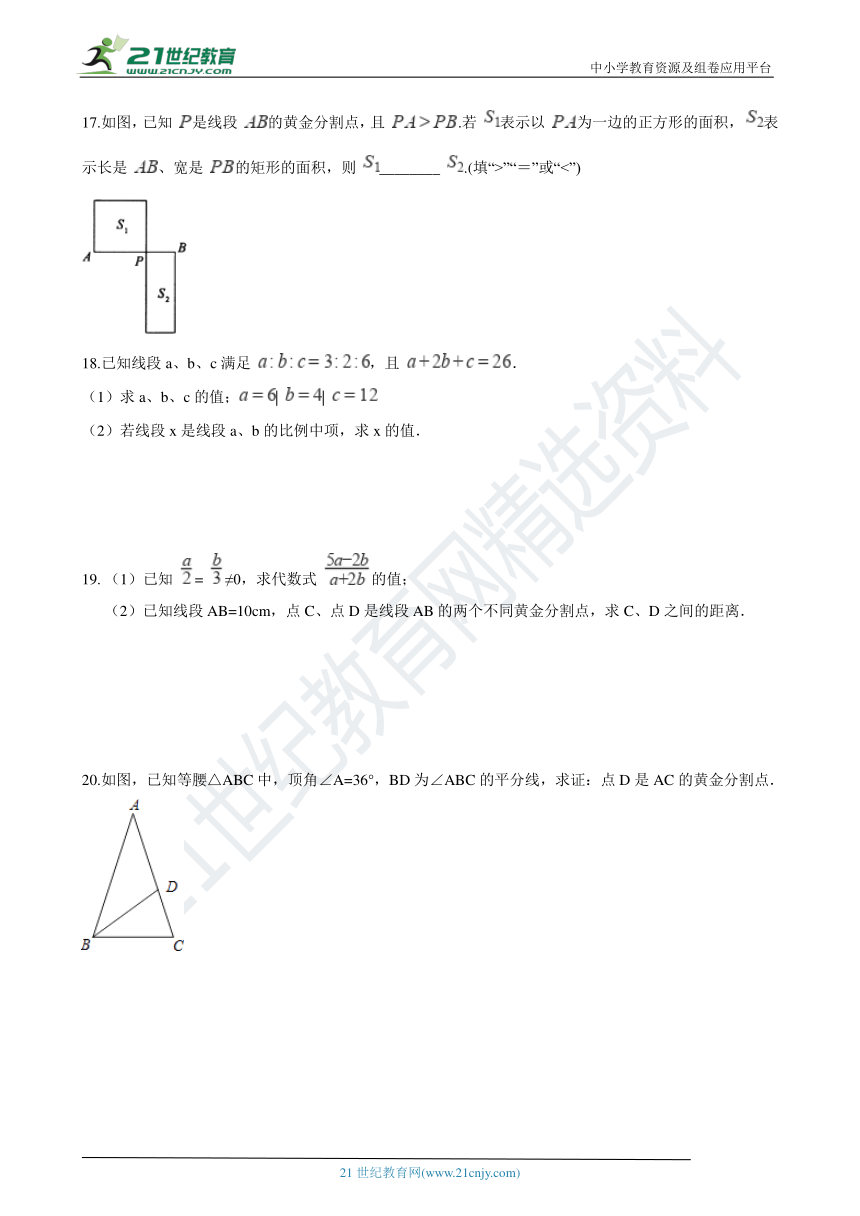
17.如图,已知 是线段 的黄金分割点,且 .若 表示以 为一边的正方形的面积, 表示长是 、宽是 的矩形的面积,则 ________ .(填“>”“=”或“<”)
18.已知线段a、b、c满足 ,且 .
(1)求a、b、c的值;| |
(2)若线段x是线段a、b的比例中项,求x的值.
19.?(1)已知 = ≠0,求代数式 的值;
(2)已知线段AB=10cm,点C、点D是线段AB的两个不同黄金分割点,求C、D之间的距离. 21*
cnjy*com
20.如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点.
答案解析部分
一、基础巩固
1.【答案】 C
解析:解:由于C为线段AB=2的黄金分割点,且AC<BC,BC为较长线段;
则BC=2× = -1.
故答案为: -1.
根据黄金分割的定义可知:, 从而得出答案。
2.【答案】 D
解析:若C是线段AB的黄金分割点,则AC=AB或BC=AB, ∴AC=或BC=, ∴BC=或。 故答案为:D。 一条线段有两个黄金分割点。若C是线段AB的黄金分割点,则AC2=AB·BC或BC2=AB·AC,再通过计算可得。
3.【答案】 D
解析:解: AB的黄金分割点为点C处,若AC>BC,则AB:AC=AC:BC,所以①不一定正确;
AC≈0.618AB≈12.36或AC≈20-12.36=7.64,所以②错误;
若AC为较长线段时,AC= AB=10( -1),BC=10(3- ); 若BC为较长线段时,BC= AB=10( -1),AC=10(3- ),所以③不一定正确,④正确.
故答案为:D
根据黄金分割的定义和AC为较长线段或较短线段进行判断,可解答。
4.【答案】 C
解析:根据黄金分割点的概念,可知AP=BQ= ,
则PQ=AP+BQ-AB= ?
故答案为:C 根据黄金分割点的概念可得AP和BQ,则PQ=AP+BQ-AB
5.【答案】C
解析:∵点 为线段 的黄金分割点,且 ,
∴ ,
即 .
故答案为: .
根据点 P 为线段 A B 的黄金分割点,A P < P B,列出比例式,即可得出结论。
6.【答案】A
解析:解:∵书的宽与长之比为黄金比,书的长为20cm,
∴书的宽约为20×0.618=12.36cm.
故选:A.
根据黄金分割的比值约为0.618列式进行计算即可得解.
7.【答案】 C
解析:解:∵b是a、c的比例中项,
∴b2=ac,即 ,
∵a:b=3:2,
∴b:c=3:2.
故答案为:C
b是a、c的比例中项则b2=ac,变形为比例式即可。
8.【答案】A
解析:解:∵线段x是a,b的比例中项,
∴x2=ab,
即x2=36,
∴x=6(负数舍去),
故选A.
根据比例中项的定义可得x2=ab,从而易求x.
9.【答案】或 或12
解析:解:设写出的线段为c,
若线段c是线段a,b的比例中项,则有c2=ab,
∵a=3,b=6,
∴c2=18,
∴c= ;
若线段a是线段c,b的比例中项,则有a2=bc,
∵a=3,b=6,
∴32=6c,
解得c= ;
若线段b是线段a,c的比例中项,则有b2=ac,
∵a=3,b=6,
∴62=3c,
解得c=12,
∴c= 或 或12,
故答案为: 或 或12.
设写出的线段为c,分三种情况讨论:若线段c是线段a,b的比例中项;若线段a是线段c,b的比例中项;若线段b是线段a,c的比例中项,分别列出比例式,解方程取出c的值即可。
10.【答案】 5 -5
解析:解:∵P为AB的黄金分割点(AP>PB),
∴AP= ?AB= ×10=5 ﹣5(cm),
故答案为:5 ﹣5
根据黄金分割的定义,PA就是AB与PB的比例中项,从而列出方程,进而得出AP= ?AB,将AB的长度代入即可算出答案。
11.【答案】 7.6
解析:根据黄金比得:20×(1-0.618)≈7.6米或20× ≈12.4米(舍去),
则主持人应走到离A点至少7.6米处.
故答案为:7.6
把一条线段分割为两部分,使较大部分与全长的比值等于较小部分与较大的比值,这个比值即为黄金分割,这个点为黄金分割点.其比值是≈0.618.此题要求主持人至少走离A点多少米,根据黄金比,只需要走到AB的1-0.618倍处即得.2·1·c·n·j·y
12.【答案】(1)解:∵a=0.3m=30cm;b=60cm,
∴a:b=30:60=1:2 (2)解:∵线段a、b、c、d是成比例线段,
∴ = ,
∵c=12dm=120cm,
∴ = ,
∴d=240cm (3)解:是,理由:
∵b2=3600,ac=30×120=3600,
∴b2=ac,
∴b是a和c的比例中项
解析:【分析】(1)首先统一单位,即a=0.3m=30cm;b=60cm,即可求得a:b的值; (2)根据线段a、b、c、d是成比例线段,可得a:b=c:d,据此可求得d的值; (3)首先计算出b2=3600,ac=30×120=3600,从而可得b2=ac,进而得出b是a和c的比例中项.
二、提高特训
13.【答案】 C
解析:∵点C数线段AB的黄金分割点,且AC>BC,
∴AC= AB,故①正确;
由AC= AB,故②错误;
BC:AC=AC:AB,即:AB:AC=AC:BC,③正确;
AC≈0.618AB,故④正确,
故答案为:C. 黄金分割是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。其比值是(√5-1):2.根据定义可得比例式求解。【版权所有:21教育】
14.【答案】 B
解析:黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618,观察图中的位置可知应该使小狗置于画面中②的位置,
故答案为:B.
黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618,观察图中的位置可知应该使小狗置于画面中②的位置,
15.【答案】 C
解析:解:由题意知,四边形AEHG、BFHG、CDEF都是矩形,
∵矩形ABCD是黄金矩形,
∴AB:AD=AB:BC= ,
∵AG=BG= AB,AE= AD,BF= BC,
∴AG:AE= AB: AD= ,BG:BF= AB: BC= ,
∴矩形AEHG、矩形BFHG是黄金矩形,
∵CD=AB,FC= BC,∴FC:CD= ≠ ,
∴图中黄金矩形共有3个,
故答案为:C.
由题意可知四边形AEHG、BFHG、CDEF都是矩形,已知矩形ABCD是黄金矩形,因此可得出AB:AD=AB:BC=, 再根据线段中点的定义证明AG:AE=BG:BF= ,就可得出矩形AEHG、矩形BFHG是黄金矩形,从而可得出黄金矩形的个数。21世纪教育网版权所有
16.【答案】
解析:解:∵C、D两点都是AB的黄金分割点,
∴ ,即 ,
∵ ,
∴ ,即 ,
解得: 或 (舍去),
又∵ ,
,
故答案为: . 由黄金分割的意义可得乘积式AD2=AC.CD,由线段的构成得AD=(AD+CD),代入可得关于AD的方程,解方程可求得AD的值,则AB=2AD+CD可求解。
17.【答案】=
解析:∵P是线段AB的黄金分割点,且PA>PB,
∴PA2=PB?AB,
又∵S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,
∴S1=PA2 , S2=PB?AB,
∴S1=S2 .
故答案为:=.
根据黄金分割的意义可得乘积式PA2=PB?AB,由题意可得S1=PA2 , S2=PB?AB,则S1=S2 .
18.【答案】(1)解:∵ ,
∴设 , , ,
又∵ ,
∴ ,解得 ,
∴ , ,
(2)解:∵x是a、b的比例中项,
∴ ,
∴ ,
∴ 或 (舍去),
即x的值为
解析:(1)根据已知条件,可设a=3k,b=2k,c=6k,然后代入方程建立关于k的方程,解方程求出k的值,就可求出a、b、c的值。 (2)利用线段x是线段a、b的比例中项,可得出x2=ab,再将a、b的值代入求出x的值。
19.【答案】(1)解:设 = =k,可得:a=2k,b=3k,
把a=2k,b=3k代入
(2)解:∵C、D是AB上的两个黄金分割点,
∴AD=BC= AB=5 ﹣5,
∴CD=AD+BC﹣AB=10 ﹣20cm.
解析:(1)利用已知可设a=2k,b=3k,再代入可求解。 (2)由点C、点D是线段AB的两个不同黄金分割点,利用黄金分割点的定义,可得出AD=BC=AB,就可求出AD、BC的长,再根据CD=AD+BC﹣AB,代入可求解。21cnjy.com
20.【答案】解:在等腰△ABC中,顶角∠A=36°, 所以∠ABC=∠C=72°, ∵BD为∠ABC的平分线, ∴∠ABD=∠DBC=36°, 在△ACB和△BCD中,∠BDC=72° ∵∠C=∠C,∠A=∠CBD=36°, ∴△ACB∽△BCD, ∴AC:BC=BC:DC; ∵∠A=∠ABD, ∴AD=BD, ∵∠DBC=36°,∠C=72°, ∴∠BDC=72°, ∴BD=BC, ∴AD=BC, ∴AC:AD=AD:DC; 即点D是AC的黄金分割点
解析:【分析】欲证点D是AC的黄金分割点,就是证明AC:AD=AD:DC,根据角平分线的性质以及已知条件推知∠C=∠C,∠A=∠CBD=36°,所以△ACB∽△BCD;然后根据相似三角形的对应边成比例求得AC:AD=AD:DC;最后由等腰三角形的性质得到:BC=BD=DA,代换即可.纪*教育网
一、基础巩固
1.已知,C是线段AB的黄金分割点,AC<BC,若AB=2,则BC=(?? )
A.?3﹣ ?????????????????????B.?( +1)?????????????????????C.?﹣1?????????????????????D.?( ﹣1)
2.点C是线段AB的黄金分割点,且AB=6cm,则BC的长为(??? )cm
A.?????????????????B.?????????????????C.?或 ????????????????D.?或
3.主持人站在舞台的黄金分割点处最自然得体,如果舞台AB长为20米,一个主持人现站在舞台AB的黄金分割点点C处,则下列结论一定正确的是(?? )21教育网
①AB:AC=AC:BC;②AC≈6.18米;③AC=10( )米;④BC=10(3? )米或10( ?1)米.
A.?①②③④??????????????????????????????????B.?①②③??????????????????????????????????C.?①③??????????????????????????????????D.?④
4.在长度为1的线段上找到两个黄金分割点P,Q,则PQ=(??? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
5.已知 为线段 的黄金分割点,且 ,则(??? ).
A.?????????????B.??????????????C.?????????????D.?
6.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20cm,则它的宽约为(?? ) 21·cn·jy·com
A.?12.36 cm???????????????????????????B.?13.6 cm???????????????????????????C.?32.36 cm???????????????????????????D.?7.64 cm
7.若a:b=3:2,且b是a、c的比例中项,则b:c等于(?? )
A.?4:3????????????????????????????????????B.?3:4????????????????????????????????????C.?3:2????????????????????????????????????D.?2:3
8.已知线段a=4,b=9,线段x是a,b的比例中项,则x等于(?? )
A.?6???????????????????????????????????????B.?6或﹣6???????????????????????????????????????C.?﹣6???????????????????????????????????????D.?36
9.若 ,请再写出一条线段的长,使它与a、b这三条线段中的一条是另外两条的比例中项,则这条线段长为________. 2-1-c-n-j-y
10.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么AP的长度为________cm. 【
11.电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB长为20m,试计算主持人应走到离A点至少________m处.(结果精确到0.1m)
12.已知线段a=0.3m,b=60cm,c=12dm.
(1)求线段a与线段b的比.
(2)如果线段a、b、c、d成比例,求线段d的长.
(3)b是a和c的比例中项吗?为什么?
二、提高特训
13.点C为线段AB的黄金分割点,且AC>BC,下列说法正确的有(?? )
①AC= AB,②AC= AB,③AB:AC=AC:BC,④AC≈0.618AB
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
14.“黄金分割”是一条举世公认的美学定律. 例如在摄影中,人们常依据黄金分割进行构图,使画面整体和谐. 目前,照相机和手机自带的九宫格就是黄金分割的简化版. 要拍摄草坪上的小狗,按照黄金分割的原则,应该使小狗置于画面中的位置(?? )21*cnjy*com
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
15.如果一个矩形的宽(即短边)与长(即长边)之比是 ,那么这个矩形称为黄金矩形.如图,矩形ABCD是黄金矩形,点E,F,G,H分别为线段AD,BC,AB,EF的中点,则图中黄金矩形的个数是(? ?)
A.?5个???????????????????????????????????????B.?4个???????????????????????????????????????C.?3个???????????????????????????????????????D.?2个
16.如图,在五角星中,AD=BC,且C、D两点都是AB的黄金分割点,CD=1,则AB的长是________.
17.如图,已知 是线段 的黄金分割点,且 .若 表示以 为一边的正方形的面积, 表示长是 、宽是 的矩形的面积,则 ________ .(填“>”“=”或“<”)
18.已知线段a、b、c满足 ,且 .
(1)求a、b、c的值;| |
(2)若线段x是线段a、b的比例中项,求x的值.
19.?(1)已知 = ≠0,求代数式 的值;
(2)已知线段AB=10cm,点C、点D是线段AB的两个不同黄金分割点,求C、D之间的距离. 21*
cnjy*com
20.如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点.
答案解析部分
一、基础巩固
1.【答案】 C
解析:解:由于C为线段AB=2的黄金分割点,且AC<BC,BC为较长线段;
则BC=2× = -1.
故答案为: -1.
根据黄金分割的定义可知:, 从而得出答案。
2.【答案】 D
解析:若C是线段AB的黄金分割点,则AC=AB或BC=AB, ∴AC=或BC=, ∴BC=或。 故答案为:D。 一条线段有两个黄金分割点。若C是线段AB的黄金分割点,则AC2=AB·BC或BC2=AB·AC,再通过计算可得。
3.【答案】 D
解析:解: AB的黄金分割点为点C处,若AC>BC,则AB:AC=AC:BC,所以①不一定正确;
AC≈0.618AB≈12.36或AC≈20-12.36=7.64,所以②错误;
若AC为较长线段时,AC= AB=10( -1),BC=10(3- ); 若BC为较长线段时,BC= AB=10( -1),AC=10(3- ),所以③不一定正确,④正确.
故答案为:D
根据黄金分割的定义和AC为较长线段或较短线段进行判断,可解答。
4.【答案】 C
解析:根据黄金分割点的概念,可知AP=BQ= ,
则PQ=AP+BQ-AB= ?
故答案为:C 根据黄金分割点的概念可得AP和BQ,则PQ=AP+BQ-AB
5.【答案】C
解析:∵点 为线段 的黄金分割点,且 ,
∴ ,
即 .
故答案为: .
根据点 P 为线段 A B 的黄金分割点,A P < P B,列出比例式,即可得出结论。
6.【答案】A
解析:解:∵书的宽与长之比为黄金比,书的长为20cm,
∴书的宽约为20×0.618=12.36cm.
故选:A.
根据黄金分割的比值约为0.618列式进行计算即可得解.
7.【答案】 C
解析:解:∵b是a、c的比例中项,
∴b2=ac,即 ,
∵a:b=3:2,
∴b:c=3:2.
故答案为:C
b是a、c的比例中项则b2=ac,变形为比例式即可。
8.【答案】A
解析:解:∵线段x是a,b的比例中项,
∴x2=ab,
即x2=36,
∴x=6(负数舍去),
故选A.
根据比例中项的定义可得x2=ab,从而易求x.
9.【答案】或 或12
解析:解:设写出的线段为c,
若线段c是线段a,b的比例中项,则有c2=ab,
∵a=3,b=6,
∴c2=18,
∴c= ;
若线段a是线段c,b的比例中项,则有a2=bc,
∵a=3,b=6,
∴32=6c,
解得c= ;
若线段b是线段a,c的比例中项,则有b2=ac,
∵a=3,b=6,
∴62=3c,
解得c=12,
∴c= 或 或12,
故答案为: 或 或12.
设写出的线段为c,分三种情况讨论:若线段c是线段a,b的比例中项;若线段a是线段c,b的比例中项;若线段b是线段a,c的比例中项,分别列出比例式,解方程取出c的值即可。
10.【答案】 5 -5
解析:解:∵P为AB的黄金分割点(AP>PB),
∴AP= ?AB= ×10=5 ﹣5(cm),
故答案为:5 ﹣5
根据黄金分割的定义,PA就是AB与PB的比例中项,从而列出方程,进而得出AP= ?AB,将AB的长度代入即可算出答案。
11.【答案】 7.6
解析:根据黄金比得:20×(1-0.618)≈7.6米或20× ≈12.4米(舍去),
则主持人应走到离A点至少7.6米处.
故答案为:7.6
把一条线段分割为两部分,使较大部分与全长的比值等于较小部分与较大的比值,这个比值即为黄金分割,这个点为黄金分割点.其比值是≈0.618.此题要求主持人至少走离A点多少米,根据黄金比,只需要走到AB的1-0.618倍处即得.2·1·c·n·j·y
12.【答案】(1)解:∵a=0.3m=30cm;b=60cm,
∴a:b=30:60=1:2 (2)解:∵线段a、b、c、d是成比例线段,
∴ = ,
∵c=12dm=120cm,
∴ = ,
∴d=240cm (3)解:是,理由:
∵b2=3600,ac=30×120=3600,
∴b2=ac,
∴b是a和c的比例中项
解析:【分析】(1)首先统一单位,即a=0.3m=30cm;b=60cm,即可求得a:b的值; (2)根据线段a、b、c、d是成比例线段,可得a:b=c:d,据此可求得d的值; (3)首先计算出b2=3600,ac=30×120=3600,从而可得b2=ac,进而得出b是a和c的比例中项.
二、提高特训
13.【答案】 C
解析:∵点C数线段AB的黄金分割点,且AC>BC,
∴AC= AB,故①正确;
由AC= AB,故②错误;
BC:AC=AC:AB,即:AB:AC=AC:BC,③正确;
AC≈0.618AB,故④正确,
故答案为:C. 黄金分割是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。其比值是(√5-1):2.根据定义可得比例式求解。【版权所有:21教育】
14.【答案】 B
解析:黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618,观察图中的位置可知应该使小狗置于画面中②的位置,
故答案为:B.
黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618,观察图中的位置可知应该使小狗置于画面中②的位置,
15.【答案】 C
解析:解:由题意知,四边形AEHG、BFHG、CDEF都是矩形,
∵矩形ABCD是黄金矩形,
∴AB:AD=AB:BC= ,
∵AG=BG= AB,AE= AD,BF= BC,
∴AG:AE= AB: AD= ,BG:BF= AB: BC= ,
∴矩形AEHG、矩形BFHG是黄金矩形,
∵CD=AB,FC= BC,∴FC:CD= ≠ ,
∴图中黄金矩形共有3个,
故答案为:C.
由题意可知四边形AEHG、BFHG、CDEF都是矩形,已知矩形ABCD是黄金矩形,因此可得出AB:AD=AB:BC=, 再根据线段中点的定义证明AG:AE=BG:BF= ,就可得出矩形AEHG、矩形BFHG是黄金矩形,从而可得出黄金矩形的个数。21世纪教育网版权所有
16.【答案】
解析:解:∵C、D两点都是AB的黄金分割点,
∴ ,即 ,
∵ ,
∴ ,即 ,
解得: 或 (舍去),
又∵ ,
,
故答案为: . 由黄金分割的意义可得乘积式AD2=AC.CD,由线段的构成得AD=(AD+CD),代入可得关于AD的方程,解方程可求得AD的值,则AB=2AD+CD可求解。
17.【答案】=
解析:∵P是线段AB的黄金分割点,且PA>PB,
∴PA2=PB?AB,
又∵S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,
∴S1=PA2 , S2=PB?AB,
∴S1=S2 .
故答案为:=.
根据黄金分割的意义可得乘积式PA2=PB?AB,由题意可得S1=PA2 , S2=PB?AB,则S1=S2 .
18.【答案】(1)解:∵ ,
∴设 , , ,
又∵ ,
∴ ,解得 ,
∴ , ,
(2)解:∵x是a、b的比例中项,
∴ ,
∴ ,
∴ 或 (舍去),
即x的值为
解析:(1)根据已知条件,可设a=3k,b=2k,c=6k,然后代入方程建立关于k的方程,解方程求出k的值,就可求出a、b、c的值。 (2)利用线段x是线段a、b的比例中项,可得出x2=ab,再将a、b的值代入求出x的值。
19.【答案】(1)解:设 = =k,可得:a=2k,b=3k,
把a=2k,b=3k代入
(2)解:∵C、D是AB上的两个黄金分割点,
∴AD=BC= AB=5 ﹣5,
∴CD=AD+BC﹣AB=10 ﹣20cm.
解析:(1)利用已知可设a=2k,b=3k,再代入可求解。 (2)由点C、点D是线段AB的两个不同黄金分割点,利用黄金分割点的定义,可得出AD=BC=AB,就可求出AD、BC的长,再根据CD=AD+BC﹣AB,代入可求解。21cnjy.com
20.【答案】解:在等腰△ABC中,顶角∠A=36°, 所以∠ABC=∠C=72°, ∵BD为∠ABC的平分线, ∴∠ABD=∠DBC=36°, 在△ACB和△BCD中,∠BDC=72° ∵∠C=∠C,∠A=∠CBD=36°, ∴△ACB∽△BCD, ∴AC:BC=BC:DC; ∵∠A=∠ABD, ∴AD=BD, ∵∠DBC=36°,∠C=72°, ∴∠BDC=72°, ∴BD=BC, ∴AD=BC, ∴AC:AD=AD:DC; 即点D是AC的黄金分割点
解析:【分析】欲证点D是AC的黄金分割点,就是证明AC:AD=AD:DC,根据角平分线的性质以及已知条件推知∠C=∠C,∠A=∠CBD=36°,所以△ACB∽△BCD;然后根据相似三角形的对应边成比例求得AC:AD=AD:DC;最后由等腰三角形的性质得到:BC=BD=DA,代换即可.纪*教育网
同课章节目录
