4.2 由平行线截得的比例线段 同步练习(解析版)
文档属性
| 名称 | 4.2 由平行线截得的比例线段 同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-29 17:21:40 | ||
图片预览


文档简介
初中数学浙教版九年级上册4.2 由平行线截得的比例线段 强化提升训练
一、单选题
1.如图是一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角 ,窗户的高在教室地面上的影长 米,窗户的下檐到教室地面的距离 米(点 、 、 在同一直线上),则窗户的高 为( ?)www.21-cn-jy.com
A.?米????????????????????????????????????B.?3米????????????????????????????????????C.?2米????????????????????????????????????D.?1.5米
2.如图,△ABC是等边三角形,AB=4,D为AB的中点,点E,F分别在线段AD,BC上,且BF=2AE,连结EF交中线AD于点G,连结BG,设AE=x(0<x<2),△BEG的面积为y,则y关于x的函数表达式是(?? ) 21*cnjy*com
A.?x2+ ????????B.?+ ????????C.?+ ????????D.?+
3.AD 是△ABC 的中线,E? 是 AD 上一点,AE= AD,BE 的延长线交 AC 于 F,则 的值为(??? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
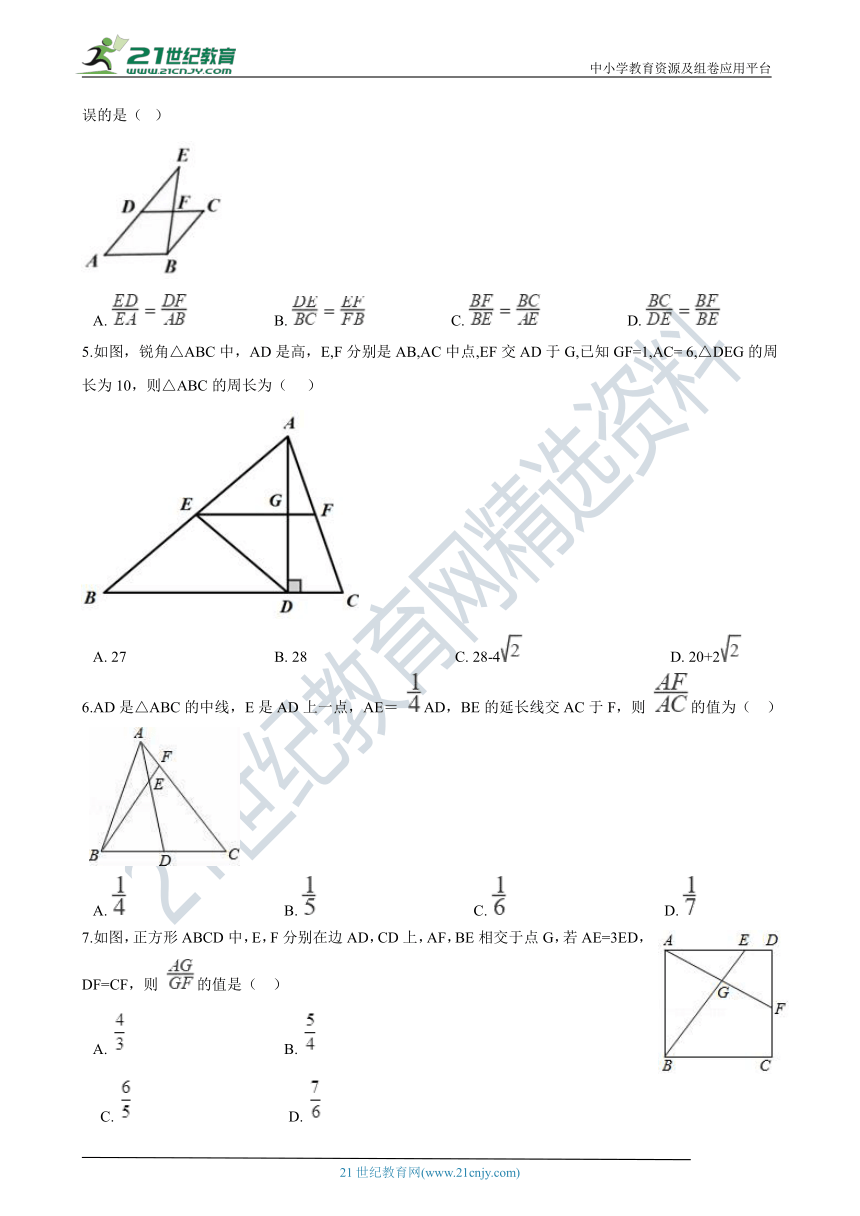
4.如图,点 是平行四边形 的边 上一点,射线 交 的延长线于点 ,则下列结论错误的是(? ) 21教育网
A.???????????????????????B.???????????????????????C.???????????????????????D.?
5.如图,锐角△ABC中,AD是高,E,F分别是AB,AC中点,EF交AD于G,已知GF=1,AC= 6,△DEG的周长为10,则△ABC的周长为( ???)
A.?27???????????????????????????????????????B.?28???????????????????????????????????????C.?28-4???????????????????????????????????????D.?20+2
6.AD是△ABC的中线,E是AD上一点,AE= AD,BE的延长线交AC于F,则 的值为(?? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
7.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则 的值是( ??)
A.??????????????????????????????????????????B.????????????????????????????????????????
??C.??????????????????????????????????????????D.?
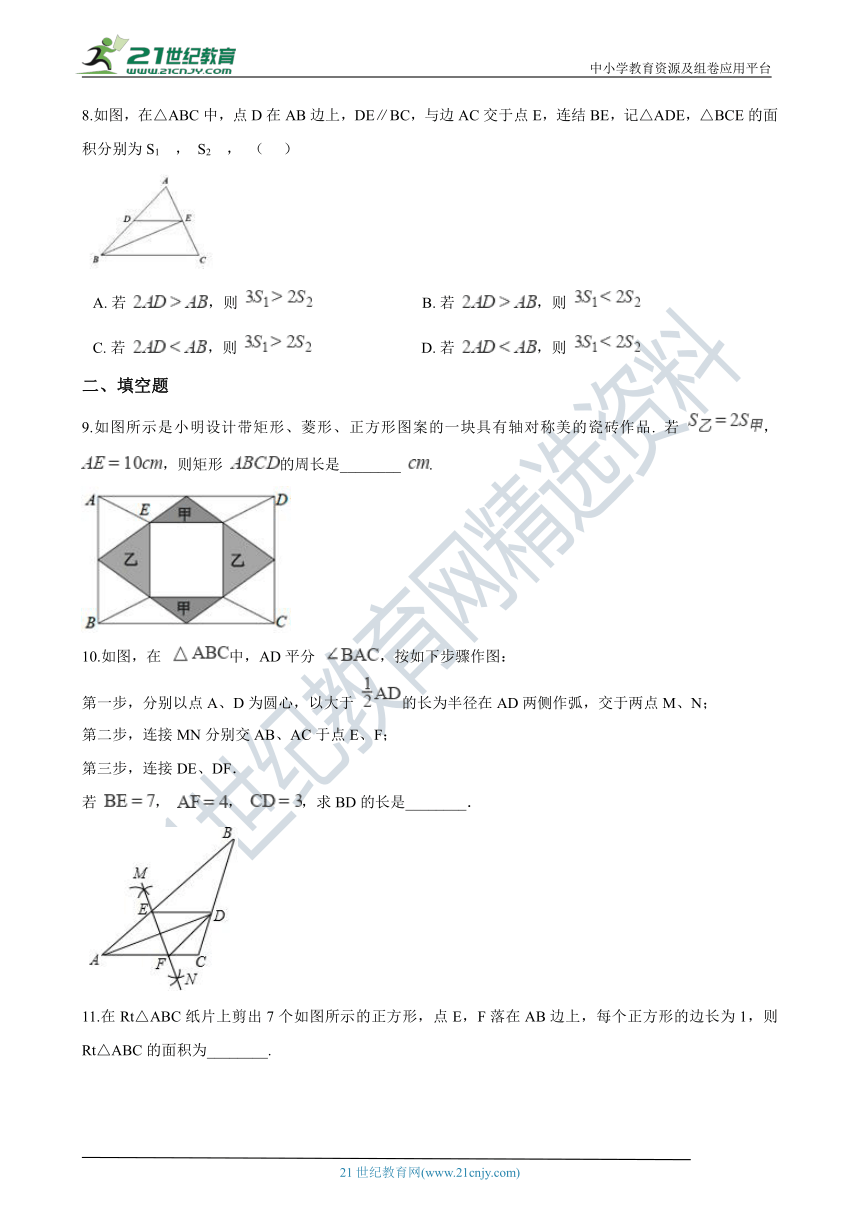
8.如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1 , S2 , (??? )
A.?若 ,则 ?????????????????????????????B.?若 ,则 C.?若 ,则 ?????????????????????????????D.?若 ,则
二、填空题
9.如图所示是小明设计带矩形、菱形、正方形图案的一块具有轴对称美的瓷砖作品. 若 , ,则矩形 的周长是________ .
10.如图,在 中,AD平分 ,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若 , , ,求BD的长是________.
11.在Rt△ABC纸片上剪出7个如图所示的正方形,点E,F落在AB边上,每个正方形的边长为1,则Rt△ABC的面积为________. 21cnjy.com
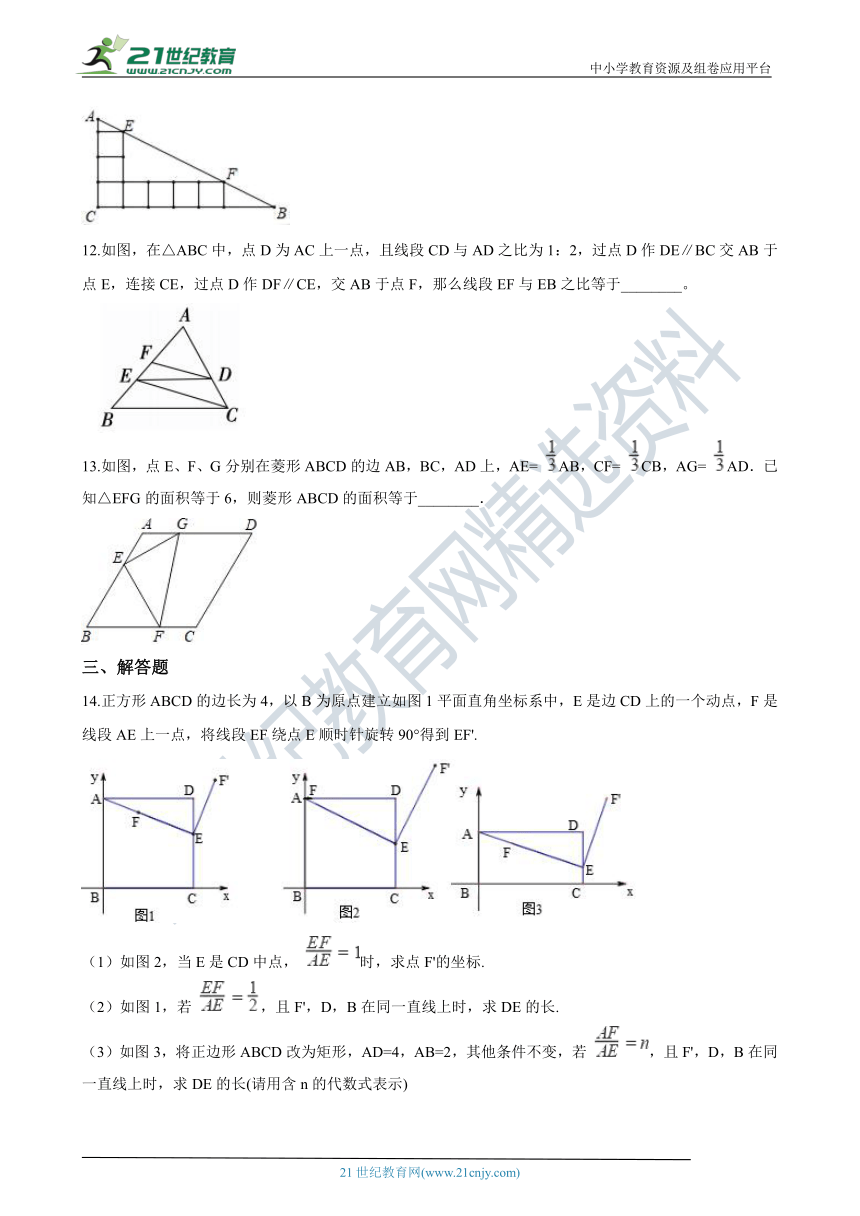
12.如图,在△ABC中,点D为AC上一点,且线段CD与AD之比为1:2,过点D作DE∥BC交AB于点E,连接CE,过点D作DF∥CE,交AB于点F,那么线段EF与EB之比等于________。
13.如图,点E、F、G分别在菱形ABCD的边AB,BC,AD上,AE= AB,CF= CB,AG= AD.已知△EFG的面积等于6,则菱形ABCD的面积等于________. 2·1·c·n·j·y
三、解答题
14.正方形ABCD的边长为4,以B为原点建立如图1平面直角坐标系中,E是边CD上的一个动点,F是线段AE上一点,将线段EF绕点E顺时针旋转90°得到EF'.
(1)如图2,当E是CD中点, 时,求点F'的坐标.
(2)如图1,若 ,且F',D,B在同一直线上时,求DE的长.
(3)如图3,将正边形ABCD改为矩形,AD=4,AB=2,其他条件不变,若 ,且F',D,B在同一直线上时,求DE的长(请用含n的代数式表示)
15.一条直线与三角形ABC的三边BC,CA,AB(或其延长线)分别交于D,E,F如图所示). 求证: .
四、中考演练
16.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为________.
17.在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B.
(1)k的值是________;
(2)点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.
①如图,点E为线段OB的中点,且四边形OCED是平行四边形时,求?OCED的周长;
②当CE平行于x轴,CD平行于y轴时,连接DE,若△CDE的面积为 ,请直接写出点C的坐标.
18.如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 (??? )
A.?1:2????????????????????????????????????B.?1:3????????????????????????????????????C.?1:4????????????????????????????????????D.?2:3
答案解析部分
一、单选题
1.【答案】 C
【解析】【解答】∵BN∥AM
∴ ?
又∵ 米
∴BN=2米,CN= 米
∴CN:CM=BC:AC
∴ ?
解得:AC=3米
∴AB=AC?BC=2米,
故答案为:C
【分析】由题意知BN∥AM,根据平行线分线段成比例定理可得比例式CN:CM=BC:AC,由比例式可求得AC的长,则AB=AC-BC求解。
2.【答案】 B
【解析】【解答】解:过点F作FH⊥AB,
∵AE=x,BF=2AE,
∴BF=2x,
在Rt△FBH中,∠FBH=60°,
∴HB=x,FH= ,
∵AB=4,D为AB的中点,
∴DE=2﹣x,DH=2﹣x,
∴GD= ,
∴y=
故答案为:B。
【分析】过点F作FH⊥AB,根据等边三角形的性质得出∠ABC=60°,在Rt△FBH中,根据含30°角的直角三角形的边之间用含x的式子表示出HB,FH的长,根据等腰三角形的三线合一及线段的和差表示出DE,DH的长,进而根据平行线分线段成比例定理用含x的式子表示出GD的长,进而根据三角形的面积计算方法即可建立出y与x的函数关系式。【版权所有:21教育】
3.【答案】 C
【解析】【解答】作DG∥AC交BF于G,如图,
∵AD是△ABC的中线,
∴BD=CD,
∵DG∥CF,
∴ = ,
∴FC=2DG,
∵DG∥AF,
∴ ,
∴ ,
∴ .
故答案为:C.
【分析】作DG∥AC交BF于G,根据三角形的中线,可证得BD=CD,再利用平行线分线段成比例定理,可求出FC=2DG,然后利用平行线分线段成比例可得AF与DG的数量关系,从而可求出AF与AC的比值。
4.【答案】 D
【解析】【解答】A、∵四边形ABCD是平行四边形,∴CD∥AB,AD∥BC,CD=AB,AD=BC,∴ = ,故A不符合题意,选项不符合题意;
B、 = 正确,B选项不符合题意;
C、 = ,正确,故C不符合题意;
D、 = ,错误,D符合题意.
故答案为:D.
【分析】利用平行四边形的性质可得CD∥AB,AD∥BC,CD=AB,AD=BC,再利用平行线分线段成比例,对各选项逐一判断,可得到结果。 ?
5.【答案】 C
【解析】【解答】解:∵ E,F分别是AB,AC中点,EF交AD于G, ∴EF∥BC,AF=AC=×6=3 ∵AD是高 ∴∠ADC=∠AGF=90° 在Rt△AGF中 AG= ∵EF∥BC ∴ ∴FG是△ADC的中位线 ∴DC=2GF=2 ∴DG=AG= ∵ △DEG的周长为10, ∴EG+DE=10- 在Rt△ADB中,点E是AB边的中点,点G是AD的中点, ∴AB=2DE,BD=2EG ∴AB+BD=2(EG+DE)=20- ∴△ABC的周长为:AB+BD+DC+AC=20-+2+6=28- 故答案为:C 【分析】利用三角形中位线定理可证EF∥BC,求出AF,利用勾股定理求出AG的长,即可求出DG的长,因此可求出EG+DE的值,再利用平行线分线段成比例定理及三角形的中位线定理求出DC的长,可证得AB+BD=2(EG+DE),就可求出AB+BD的值,然后求出△ABC的周长。
6.【答案】 D
【解析】【解答】解:作DH∥BF交AC于H,
∵AD是△ABC的中线,
∴FH=HC,
∵DH∥BF,AE= AD,
∴ ,
∴AF:FC=1:6,
∴ 的值为 .
故答案为:D.
【分析】根据平行线分线段成比例定理得到FH=HC,, 从而得到的值.
7.【答案】 C
【解析】【解答】如图作,FN∥AD,交AB于N,交BE于M.
∵四边形ABCD是正方形,
∴AB∥CD,∵FN∥AD,
∴四边形ANFD是平行四边形,
∵∠D=90°,
∴四边形ANFD是矩形,
∵AE=3DE,设DE=a,则AE=3a,AD=AB=CD=FN=4a,AN=DF=2a,
∵AN=BN,MN∥AE,
∴BM=ME,
∴MN= a,
∴FM= a,
∵AE∥FM,
∴ ,
故答案为:C. 【分析】如图作,FN∥AD,交AB于N,交BE于M,根据正方形的性质得出AB∥CD,∠D=90°,从而根据两组对边分别平行的四边形是平行四边形得出四边形ANFD是平行四边形,再根据有一个角是直角的平行四边形是矩形得出四边形ANFD是矩形,AE=3DE,设DE=a,则AE=3a,AD=AB=CD=FN=4a,AN=DF=2a,根据过三角形一边中点,且平行于另一边的直线一定平分第三边得出BM=ME,根据三角形的中位线定理得出MN= a,然后根据平行线分线段成比例定理得出, 从而得出答案。
8.【答案】D
【解析】【解答】解:如图,过点D作DF⊥AC于点F,过点B作BM⊥AC于点M
∴DF∥BM,设DF=h1 , BM=h2
∴
∵DE∥BC
∴
∴
∵若
∴设 =k<0.5(0<k<0.5)
∴AE=AC?k,CE=AC-AE=AC(1-k),h1=h2k
∵S1= AE?h1= AC?k?h1 , S2= CE?h2= AC(1-k)h2
∴3S1= k2ACh2 , 2S2=(1-K)?ACh2
∵0<k<0.5
∴ k2<(1-K)
∴3S1<2S2
故答案为:D
【分析】过点D作DF⊥AC于点F,过点B作BM⊥AC于点M,可得出DF∥BM,设DF=h1 , BM=h2 , 再根据DE∥BC,可证得 ,若 ,设 =k<0.5(0<k<0.5),再分别求出3S1和2S2 , 根据k的取值范围,即可得出答案。21·世纪*教育网
二、填空题
9.【答案】
【解析】【解答】如图,作EM⊥AB于M,EN⊥AD于N,连接KT,作RQ⊥KT于Q,交EW于O.
由若S乙=2S甲 , 可得EM=2EN,设EN=x,则AN=EM=2x,则有x2+(2x)2=102 ,
∴EN=2 AN=EM=4 ,
设OE=OQ=y,
∵WE∥KT,
,
,
,
∴四边形ABCD的周长= ,
故答案是: .
【分析】作EM⊥AB于M,EN⊥AD于N,连接KT,作RQ⊥KT于Q,交EW于O,由甲、乙两个三角形的面积的关系可得EM=2EN,设EN=x,则AN=EM=2x,在直角三角形ANE中,用勾股定理可得关于x的方程,解方程可求得x的值,于是EN、AN=EM的值可求解;设OE=OQ=y,由平行线分线段成比例定理可得比例式, 根据比例式可求得y的值,则四边形ABCD的周长可求解。
10.【答案】
【解析】【解答】解:由作法得MN垂直平分AD,则AE=DE,FA=FD,
∵AD平分∠EAF,AD⊥EF,
∴△AEF为等腰三角形,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF为菱形,
∴AE=AF=4,DE∥AC,
∴ = ,即 = ,
∴BD=
故答案为 .
【分析】由作法可得MN垂直平分AD,AE=DE,FA=FD, 利用三角形全等(ASA)可判断△AEF为等腰三角形,根据四边相等可得四边形AEDF为菱形,进而可得DE∥AC,由平行线分线段成比例定理即可得出答案.
11.【答案】
【解析】【解答】解:如图,设AH=x,GB=y,
∵EH∥BC,
,
∵FG∥AC,
,
由①②可得x= ,y=2,
∴AC= ,BC=7,
∴S△ABC= ,
故答案为 .
【分析】设AH=x,GB=y,再利用平行线分线段成比例定理,由EH∥BC,FG∥AC,可得出对应线段成比例,建立关于x,y的方程组,解方程组求出x,y的值,从而可求出AC,BC的值,然后利用直角三角形的面积公式就可求出△ABC的面积。
12.【答案】 2:3
【解析】【解答】∵DE∥BC,∴=2, ∴AE=2BE,BE= 又DF∥CE, ∴, AF=2EF,又AF+EF=AE, ∴EF= ∴=。 故答案为:2:3。 【分析】根据平行线分线段成比例,分别得到EF、EB与AE的关系,即用AE表示出EF与EB,然后求出两者之比即可。
13.【答案】27
【解析】【解答】如图,在CD上截取一点H,使得CH= CD,连接AC交BD于O,BD交EF于Q,EG交AC于P, ∵AE= AB,AG= AD, ∴ , ∴EG∥BD,同法可证:FH∥BD, ∴EG∥FH,同法可证EF∥GF, ∴四边形EFGH是平行四边形, ∵四边形ABCD是菱形, ∴AC⊥BD, ∴EF⊥EG, ∴四边形EFGH是矩形,易证点O在线段FG上,四边形EQOP是矩形, ∵S△EFG=6, ∴S矩形EQOP=3,即OP?OQ=3, ∵OP:OA=BE:AB=2:3, ∴OA= OP,同法可证OB=3OQ, ∴S菱形ABCD= ?AC?BD= ×3OP×6OQ=9OP×OQ=27, 故答案为:27. 【分析】如图,在CD上截取一点H,使得CH=?CD,连接AC交BD于O,BD交EF于Q,EG交AC于P,根据平行线分线段成比例定理得逆用判断出EG∥BD,同法可证:FH∥BD,根据平行于同一直线的两条直线互相平行得出EG∥FH,同法可证EF∥GF,根据两组对边分别平行的四边形是平行四边形得出四边形EFGH是平行四边形,根据菱形的对角线互相平行及平行线的性质得出EF⊥EG,根据有一个角是直角的平行四边形是矩形得出四边形EFGH是矩形,易证点O在线段FG上,四边形EQOP是矩形,根据矩形的性质,及平行线分线段成比例定理得出OA=?OP,同法可证OB=3OQ,根据菱形的面积等于两对角线积的一半,用整体代入即可算出答案。【出处:21教育名师】
三、解答题
14.【答案】 (1)解:如图2,作EM⊥AB于M, 交CD延长线于H,
∵E是CD中点,
∴四边形AMED是矩形,
∵∠AME=∠AEF'=∠MEH=∠H=90°,
∴∠AEM+∠AEH=90°,∠AEH+∠HEF'=90°,
∴∠AEM=∠HEF',EA=EF',
∴△AME≌△F'HE,
∴AM=F'H=2,EM=EH=4,
∴F'(6,6) (2)解:如图1,作FM⊥CD于M,F'H⊥CD交CD延长线于H,连接BF',
设DE=x,
∵ ,
∴AF=EF,
∵FM∥AD,∴DM=ME= ,FM= ,
∠AEM+∠HEF'=90°,∠AEM+∠MFE=90°,
∴∠HEF'=∠MFE,
因为∠FME=∠HF'E=90°,EF=EF',
∴△FME≌△EHF',
∴HF'=ME= ,EH=FM=2,
∵四边形ABCD是正方形,
∴∠HDF'=∠BDC=45°,
∴DH=HF'= ,
∴ ,
解得 ,
∴DE= (3)解:∵FM∥AD,∴ ,
∴FM=4-4n,EM=x-xn,
由(2)可知△FME≌△EHF',
∴HF'=EM=x-xn,EH=FM=4-4n,
∵ ,
∴DH= ,
∴ ,
∴ ,
即 .
【解析】【分析】(1) 如图2,作EM⊥AB于M, 交CD延长线于H,利用同角的余角相等证出 ∠AEM=∠HEF',根据AAS可判断△AME≌△F'HE,由全等三角形的对应边相等可得AM=F'H=2,EM=EH=4,进而求出F'(6,6).(2) 如图1,作FM⊥CD于M,F'H⊥CD交CD延长线于H,连接BF', 设DE=x, 利用平行线分线段成比例定理可得DM=ME= ,FM= , 根据同角的余角相等可得∠HEF'=∠MFE,利用AAS判断△FME≌△EHF',由全等三角形的对应边相等可得 HF'=ME= ,EH=FM=2, 根据正方形的对角线及对顶角的性质可得∠HDF'=∠BDC=45°,DH=HF'= ,根据EH=FM=2可得方程 ,解方程求出x,即可求出DE的长.(3)利用平行线分线段成比例定理可得 ,进而可得FM=4-4n,EM=x-xn,利用AAS判断△FME≌△EHF',进而可得HF'=EM=x-xn,EH=FM=4-4n,根据对顶角相等可得 ,从中求出DH= ,根据EH=FM
列出方程,解方程求出x的值即为DE的长.
15.【答案】解:证明. 证明:过B作BG∥EF,交AC于G.由平行线分线段成比例性质知 = , ?= , ∴ × × = × × =1 【来源:21·世纪·教育·网】
【解析】【分析】过B作BG∥EF,交AC于G,利用平行线分线段成比例,可得出对应相等成比例,然后根据等量代换,可证得结论。
四、中考演练
16.【答案】
【解析】【解答】解:作AM⊥BC于E,如图所示,
∵CD平分∠ACB,
∴ ,
设AC=2x,则BC=3x,
∵MN是BC的垂直平分线,
∴MN⊥BC,BN=CN= x,
∴MN∥AE,
∴ ,
∴NE=x,
∴BE=BN+EN= x,CE=CN?EN= x,
由勾股定理得:AE2=AB2?BE2=AC2?CE2 ,
即52?( x)2=(2x)2?( x)2 ,
解得:x= ,
∴AC=2x= ;
故答案为: . 【分析】作AM⊥BC于E,如图所示,根据角平分线的性质定理得出, 设AC=2x,则BC=3x,根据中垂线的定义得出MN⊥BC,BN=CN= x,根据同一平面内垂直于同一直线的两条直线互相平行得出MN∥AE,根据平行线分线段成比例定理得出, 故NE=x,在Rt△ABE中,根据勾股定理建立方程求解即可求出x的值,从而算出AC的长。www-2-1-cnjy-com
17.【答案】 (1) (2)①由(1)可知直线AB的解析式为y= x+4.
当x=0时,y= x+4=4,
∴点B的坐标为(0,4),
∴OB=4.
∵点E为OB的中点,
∴BE=OE= OB=2.
∵点A的坐标为(8,0),
∴OA=8.
∵四边形OCED是平行四边形,
∴CE∥DA,
∴ ,
∴BC=AC,
∴CE是△ABO的中位线,
∴CE= OA=4.
∵四边形OCED是平行四边形,
∴OD=CE=4,OC=DE.
在Rt△DOE中,∠DOE=90°,OD=4,OE=2,
∴DE= ,
∴C平行四边形OCED=2(OD+DE)=2(4+2 )=8+4 .
②设点C的坐标为(x, +4),则CE=|x|,CD=| x+4|,
∴S△CDE= CD?CE=|﹣ x2+2x|= ,
∴x2+8x+33=0或x2+8x﹣33=0.
方程x2+8x+33=0无解;
解方程x2+8x﹣33=0,得:x1=﹣3,x2=11,
∴点C的坐标为(﹣3, )或(11, ).
【解析】【解答】(1)将A(8,0)代入y=kx+4,得:0=8k+4,
解得:k= .
故答案为: 。
【分析】(1)将点A的坐标代入直线y=kx+4(k≠0) 即可算出k的值,从而求出一次函数的解析式; (2) ① 根据直线与y轴交点的坐标特点,求出点B的坐标,从而得出OB的长度,根据中点的定义得出BE=OE=2,根据平行四边形的对边平行得出 CE∥DA, 根据平行线分线段成比例定理得出 ,所以点C是AB的中点, 进而根据三角形的中位线定理得出 CE= OA=4, 在Rt△DOE中 ,利用勾股定理算出DE长,从而根据平行四边形周长的计算方法即可算出答案; ② 根据点的坐标与图形的性质设出点C的坐标,然后根据三角形的面积计算方法,由 △CDE的面积为 建立方程,求解即可得出x的值,从而求出点C的坐标。
18.【答案】 B
【解析】【解答】解:如图,过O作 ,交AC于G,
∵O是BD的中点,
∴G是DC的中点.
又 ,
设 ,又 ,
,
故答案为:B.
【分析】如图,过O作 ,交AC于G,根据平行线分线段成比例可得出AD:DC=1:2,从而可得AD=DG=GC,AG:GC=2:1,AO:OE=2:1,由△AOB与△BOE同高,可得S△AOB:S△BOE=AO:OE=2:1,由同高不同底的三角形中底与三角形的面积关系即可BE:FC的比.21教育名师原创作品
一、单选题
1.如图是一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角 ,窗户的高在教室地面上的影长 米,窗户的下檐到教室地面的距离 米(点 、 、 在同一直线上),则窗户的高 为( ?)www.21-cn-jy.com
A.?米????????????????????????????????????B.?3米????????????????????????????????????C.?2米????????????????????????????????????D.?1.5米
2.如图,△ABC是等边三角形,AB=4,D为AB的中点,点E,F分别在线段AD,BC上,且BF=2AE,连结EF交中线AD于点G,连结BG,设AE=x(0<x<2),△BEG的面积为y,则y关于x的函数表达式是(?? ) 21*cnjy*com
A.?x2+ ????????B.?+ ????????C.?+ ????????D.?+
3.AD 是△ABC 的中线,E? 是 AD 上一点,AE= AD,BE 的延长线交 AC 于 F,则 的值为(??? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
4.如图,点 是平行四边形 的边 上一点,射线 交 的延长线于点 ,则下列结论错误的是(? ) 21教育网
A.???????????????????????B.???????????????????????C.???????????????????????D.?
5.如图,锐角△ABC中,AD是高,E,F分别是AB,AC中点,EF交AD于G,已知GF=1,AC= 6,△DEG的周长为10,则△ABC的周长为( ???)
A.?27???????????????????????????????????????B.?28???????????????????????????????????????C.?28-4???????????????????????????????????????D.?20+2
6.AD是△ABC的中线,E是AD上一点,AE= AD,BE的延长线交AC于F,则 的值为(?? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
7.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则 的值是( ??)
A.??????????????????????????????????????????B.????????????????????????????????????????
??C.??????????????????????????????????????????D.?
8.如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1 , S2 , (??? )
A.?若 ,则 ?????????????????????????????B.?若 ,则 C.?若 ,则 ?????????????????????????????D.?若 ,则
二、填空题
9.如图所示是小明设计带矩形、菱形、正方形图案的一块具有轴对称美的瓷砖作品. 若 , ,则矩形 的周长是________ .
10.如图,在 中,AD平分 ,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若 , , ,求BD的长是________.
11.在Rt△ABC纸片上剪出7个如图所示的正方形,点E,F落在AB边上,每个正方形的边长为1,则Rt△ABC的面积为________. 21cnjy.com
12.如图,在△ABC中,点D为AC上一点,且线段CD与AD之比为1:2,过点D作DE∥BC交AB于点E,连接CE,过点D作DF∥CE,交AB于点F,那么线段EF与EB之比等于________。
13.如图,点E、F、G分别在菱形ABCD的边AB,BC,AD上,AE= AB,CF= CB,AG= AD.已知△EFG的面积等于6,则菱形ABCD的面积等于________. 2·1·c·n·j·y
三、解答题
14.正方形ABCD的边长为4,以B为原点建立如图1平面直角坐标系中,E是边CD上的一个动点,F是线段AE上一点,将线段EF绕点E顺时针旋转90°得到EF'.
(1)如图2,当E是CD中点, 时,求点F'的坐标.
(2)如图1,若 ,且F',D,B在同一直线上时,求DE的长.
(3)如图3,将正边形ABCD改为矩形,AD=4,AB=2,其他条件不变,若 ,且F',D,B在同一直线上时,求DE的长(请用含n的代数式表示)
15.一条直线与三角形ABC的三边BC,CA,AB(或其延长线)分别交于D,E,F如图所示). 求证: .
四、中考演练
16.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为________.
17.在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B.
(1)k的值是________;
(2)点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.
①如图,点E为线段OB的中点,且四边形OCED是平行四边形时,求?OCED的周长;
②当CE平行于x轴,CD平行于y轴时,连接DE,若△CDE的面积为 ,请直接写出点C的坐标.
18.如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 (??? )
A.?1:2????????????????????????????????????B.?1:3????????????????????????????????????C.?1:4????????????????????????????????????D.?2:3
答案解析部分
一、单选题
1.【答案】 C
【解析】【解答】∵BN∥AM
∴ ?
又∵ 米
∴BN=2米,CN= 米
∴CN:CM=BC:AC
∴ ?
解得:AC=3米
∴AB=AC?BC=2米,
故答案为:C
【分析】由题意知BN∥AM,根据平行线分线段成比例定理可得比例式CN:CM=BC:AC,由比例式可求得AC的长,则AB=AC-BC求解。
2.【答案】 B
【解析】【解答】解:过点F作FH⊥AB,
∵AE=x,BF=2AE,
∴BF=2x,
在Rt△FBH中,∠FBH=60°,
∴HB=x,FH= ,
∵AB=4,D为AB的中点,
∴DE=2﹣x,DH=2﹣x,
∴GD= ,
∴y=
故答案为:B。
【分析】过点F作FH⊥AB,根据等边三角形的性质得出∠ABC=60°,在Rt△FBH中,根据含30°角的直角三角形的边之间用含x的式子表示出HB,FH的长,根据等腰三角形的三线合一及线段的和差表示出DE,DH的长,进而根据平行线分线段成比例定理用含x的式子表示出GD的长,进而根据三角形的面积计算方法即可建立出y与x的函数关系式。【版权所有:21教育】
3.【答案】 C
【解析】【解答】作DG∥AC交BF于G,如图,
∵AD是△ABC的中线,
∴BD=CD,
∵DG∥CF,
∴ = ,
∴FC=2DG,
∵DG∥AF,
∴ ,
∴ ,
∴ .
故答案为:C.
【分析】作DG∥AC交BF于G,根据三角形的中线,可证得BD=CD,再利用平行线分线段成比例定理,可求出FC=2DG,然后利用平行线分线段成比例可得AF与DG的数量关系,从而可求出AF与AC的比值。
4.【答案】 D
【解析】【解答】A、∵四边形ABCD是平行四边形,∴CD∥AB,AD∥BC,CD=AB,AD=BC,∴ = ,故A不符合题意,选项不符合题意;
B、 = 正确,B选项不符合题意;
C、 = ,正确,故C不符合题意;
D、 = ,错误,D符合题意.
故答案为:D.
【分析】利用平行四边形的性质可得CD∥AB,AD∥BC,CD=AB,AD=BC,再利用平行线分线段成比例,对各选项逐一判断,可得到结果。 ?
5.【答案】 C
【解析】【解答】解:∵ E,F分别是AB,AC中点,EF交AD于G, ∴EF∥BC,AF=AC=×6=3 ∵AD是高 ∴∠ADC=∠AGF=90° 在Rt△AGF中 AG= ∵EF∥BC ∴ ∴FG是△ADC的中位线 ∴DC=2GF=2 ∴DG=AG= ∵ △DEG的周长为10, ∴EG+DE=10- 在Rt△ADB中,点E是AB边的中点,点G是AD的中点, ∴AB=2DE,BD=2EG ∴AB+BD=2(EG+DE)=20- ∴△ABC的周长为:AB+BD+DC+AC=20-+2+6=28- 故答案为:C 【分析】利用三角形中位线定理可证EF∥BC,求出AF,利用勾股定理求出AG的长,即可求出DG的长,因此可求出EG+DE的值,再利用平行线分线段成比例定理及三角形的中位线定理求出DC的长,可证得AB+BD=2(EG+DE),就可求出AB+BD的值,然后求出△ABC的周长。
6.【答案】 D
【解析】【解答】解:作DH∥BF交AC于H,
∵AD是△ABC的中线,
∴FH=HC,
∵DH∥BF,AE= AD,
∴ ,
∴AF:FC=1:6,
∴ 的值为 .
故答案为:D.
【分析】根据平行线分线段成比例定理得到FH=HC,, 从而得到的值.
7.【答案】 C
【解析】【解答】如图作,FN∥AD,交AB于N,交BE于M.
∵四边形ABCD是正方形,
∴AB∥CD,∵FN∥AD,
∴四边形ANFD是平行四边形,
∵∠D=90°,
∴四边形ANFD是矩形,
∵AE=3DE,设DE=a,则AE=3a,AD=AB=CD=FN=4a,AN=DF=2a,
∵AN=BN,MN∥AE,
∴BM=ME,
∴MN= a,
∴FM= a,
∵AE∥FM,
∴ ,
故答案为:C. 【分析】如图作,FN∥AD,交AB于N,交BE于M,根据正方形的性质得出AB∥CD,∠D=90°,从而根据两组对边分别平行的四边形是平行四边形得出四边形ANFD是平行四边形,再根据有一个角是直角的平行四边形是矩形得出四边形ANFD是矩形,AE=3DE,设DE=a,则AE=3a,AD=AB=CD=FN=4a,AN=DF=2a,根据过三角形一边中点,且平行于另一边的直线一定平分第三边得出BM=ME,根据三角形的中位线定理得出MN= a,然后根据平行线分线段成比例定理得出, 从而得出答案。
8.【答案】D
【解析】【解答】解:如图,过点D作DF⊥AC于点F,过点B作BM⊥AC于点M
∴DF∥BM,设DF=h1 , BM=h2
∴
∵DE∥BC
∴
∴
∵若
∴设 =k<0.5(0<k<0.5)
∴AE=AC?k,CE=AC-AE=AC(1-k),h1=h2k
∵S1= AE?h1= AC?k?h1 , S2= CE?h2= AC(1-k)h2
∴3S1= k2ACh2 , 2S2=(1-K)?ACh2
∵0<k<0.5
∴ k2<(1-K)
∴3S1<2S2
故答案为:D
【分析】过点D作DF⊥AC于点F,过点B作BM⊥AC于点M,可得出DF∥BM,设DF=h1 , BM=h2 , 再根据DE∥BC,可证得 ,若 ,设 =k<0.5(0<k<0.5),再分别求出3S1和2S2 , 根据k的取值范围,即可得出答案。21·世纪*教育网
二、填空题
9.【答案】
【解析】【解答】如图,作EM⊥AB于M,EN⊥AD于N,连接KT,作RQ⊥KT于Q,交EW于O.
由若S乙=2S甲 , 可得EM=2EN,设EN=x,则AN=EM=2x,则有x2+(2x)2=102 ,
∴EN=2 AN=EM=4 ,
设OE=OQ=y,
∵WE∥KT,
,
,
,
∴四边形ABCD的周长= ,
故答案是: .
【分析】作EM⊥AB于M,EN⊥AD于N,连接KT,作RQ⊥KT于Q,交EW于O,由甲、乙两个三角形的面积的关系可得EM=2EN,设EN=x,则AN=EM=2x,在直角三角形ANE中,用勾股定理可得关于x的方程,解方程可求得x的值,于是EN、AN=EM的值可求解;设OE=OQ=y,由平行线分线段成比例定理可得比例式, 根据比例式可求得y的值,则四边形ABCD的周长可求解。
10.【答案】
【解析】【解答】解:由作法得MN垂直平分AD,则AE=DE,FA=FD,
∵AD平分∠EAF,AD⊥EF,
∴△AEF为等腰三角形,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF为菱形,
∴AE=AF=4,DE∥AC,
∴ = ,即 = ,
∴BD=
故答案为 .
【分析】由作法可得MN垂直平分AD,AE=DE,FA=FD, 利用三角形全等(ASA)可判断△AEF为等腰三角形,根据四边相等可得四边形AEDF为菱形,进而可得DE∥AC,由平行线分线段成比例定理即可得出答案.
11.【答案】
【解析】【解答】解:如图,设AH=x,GB=y,
∵EH∥BC,
,
∵FG∥AC,
,
由①②可得x= ,y=2,
∴AC= ,BC=7,
∴S△ABC= ,
故答案为 .
【分析】设AH=x,GB=y,再利用平行线分线段成比例定理,由EH∥BC,FG∥AC,可得出对应线段成比例,建立关于x,y的方程组,解方程组求出x,y的值,从而可求出AC,BC的值,然后利用直角三角形的面积公式就可求出△ABC的面积。
12.【答案】 2:3
【解析】【解答】∵DE∥BC,∴=2, ∴AE=2BE,BE= 又DF∥CE, ∴, AF=2EF,又AF+EF=AE, ∴EF= ∴=。 故答案为:2:3。 【分析】根据平行线分线段成比例,分别得到EF、EB与AE的关系,即用AE表示出EF与EB,然后求出两者之比即可。
13.【答案】27
【解析】【解答】如图,在CD上截取一点H,使得CH= CD,连接AC交BD于O,BD交EF于Q,EG交AC于P, ∵AE= AB,AG= AD, ∴ , ∴EG∥BD,同法可证:FH∥BD, ∴EG∥FH,同法可证EF∥GF, ∴四边形EFGH是平行四边形, ∵四边形ABCD是菱形, ∴AC⊥BD, ∴EF⊥EG, ∴四边形EFGH是矩形,易证点O在线段FG上,四边形EQOP是矩形, ∵S△EFG=6, ∴S矩形EQOP=3,即OP?OQ=3, ∵OP:OA=BE:AB=2:3, ∴OA= OP,同法可证OB=3OQ, ∴S菱形ABCD= ?AC?BD= ×3OP×6OQ=9OP×OQ=27, 故答案为:27. 【分析】如图,在CD上截取一点H,使得CH=?CD,连接AC交BD于O,BD交EF于Q,EG交AC于P,根据平行线分线段成比例定理得逆用判断出EG∥BD,同法可证:FH∥BD,根据平行于同一直线的两条直线互相平行得出EG∥FH,同法可证EF∥GF,根据两组对边分别平行的四边形是平行四边形得出四边形EFGH是平行四边形,根据菱形的对角线互相平行及平行线的性质得出EF⊥EG,根据有一个角是直角的平行四边形是矩形得出四边形EFGH是矩形,易证点O在线段FG上,四边形EQOP是矩形,根据矩形的性质,及平行线分线段成比例定理得出OA=?OP,同法可证OB=3OQ,根据菱形的面积等于两对角线积的一半,用整体代入即可算出答案。【出处:21教育名师】
三、解答题
14.【答案】 (1)解:如图2,作EM⊥AB于M, 交CD延长线于H,
∵E是CD中点,
∴四边形AMED是矩形,
∵∠AME=∠AEF'=∠MEH=∠H=90°,
∴∠AEM+∠AEH=90°,∠AEH+∠HEF'=90°,
∴∠AEM=∠HEF',EA=EF',
∴△AME≌△F'HE,
∴AM=F'H=2,EM=EH=4,
∴F'(6,6) (2)解:如图1,作FM⊥CD于M,F'H⊥CD交CD延长线于H,连接BF',
设DE=x,
∵ ,
∴AF=EF,
∵FM∥AD,∴DM=ME= ,FM= ,
∠AEM+∠HEF'=90°,∠AEM+∠MFE=90°,
∴∠HEF'=∠MFE,
因为∠FME=∠HF'E=90°,EF=EF',
∴△FME≌△EHF',
∴HF'=ME= ,EH=FM=2,
∵四边形ABCD是正方形,
∴∠HDF'=∠BDC=45°,
∴DH=HF'= ,
∴ ,
解得 ,
∴DE= (3)解:∵FM∥AD,∴ ,
∴FM=4-4n,EM=x-xn,
由(2)可知△FME≌△EHF',
∴HF'=EM=x-xn,EH=FM=4-4n,
∵ ,
∴DH= ,
∴ ,
∴ ,
即 .
【解析】【分析】(1) 如图2,作EM⊥AB于M, 交CD延长线于H,利用同角的余角相等证出 ∠AEM=∠HEF',根据AAS可判断△AME≌△F'HE,由全等三角形的对应边相等可得AM=F'H=2,EM=EH=4,进而求出F'(6,6).(2) 如图1,作FM⊥CD于M,F'H⊥CD交CD延长线于H,连接BF', 设DE=x, 利用平行线分线段成比例定理可得DM=ME= ,FM= , 根据同角的余角相等可得∠HEF'=∠MFE,利用AAS判断△FME≌△EHF',由全等三角形的对应边相等可得 HF'=ME= ,EH=FM=2, 根据正方形的对角线及对顶角的性质可得∠HDF'=∠BDC=45°,DH=HF'= ,根据EH=FM=2可得方程 ,解方程求出x,即可求出DE的长.(3)利用平行线分线段成比例定理可得 ,进而可得FM=4-4n,EM=x-xn,利用AAS判断△FME≌△EHF',进而可得HF'=EM=x-xn,EH=FM=4-4n,根据对顶角相等可得 ,从中求出DH= ,根据EH=FM
列出方程,解方程求出x的值即为DE的长.
15.【答案】解:证明. 证明:过B作BG∥EF,交AC于G.由平行线分线段成比例性质知 = , ?= , ∴ × × = × × =1 【来源:21·世纪·教育·网】
【解析】【分析】过B作BG∥EF,交AC于G,利用平行线分线段成比例,可得出对应相等成比例,然后根据等量代换,可证得结论。
四、中考演练
16.【答案】
【解析】【解答】解:作AM⊥BC于E,如图所示,
∵CD平分∠ACB,
∴ ,
设AC=2x,则BC=3x,
∵MN是BC的垂直平分线,
∴MN⊥BC,BN=CN= x,
∴MN∥AE,
∴ ,
∴NE=x,
∴BE=BN+EN= x,CE=CN?EN= x,
由勾股定理得:AE2=AB2?BE2=AC2?CE2 ,
即52?( x)2=(2x)2?( x)2 ,
解得:x= ,
∴AC=2x= ;
故答案为: . 【分析】作AM⊥BC于E,如图所示,根据角平分线的性质定理得出, 设AC=2x,则BC=3x,根据中垂线的定义得出MN⊥BC,BN=CN= x,根据同一平面内垂直于同一直线的两条直线互相平行得出MN∥AE,根据平行线分线段成比例定理得出, 故NE=x,在Rt△ABE中,根据勾股定理建立方程求解即可求出x的值,从而算出AC的长。www-2-1-cnjy-com
17.【答案】 (1) (2)①由(1)可知直线AB的解析式为y= x+4.
当x=0时,y= x+4=4,
∴点B的坐标为(0,4),
∴OB=4.
∵点E为OB的中点,
∴BE=OE= OB=2.
∵点A的坐标为(8,0),
∴OA=8.
∵四边形OCED是平行四边形,
∴CE∥DA,
∴ ,
∴BC=AC,
∴CE是△ABO的中位线,
∴CE= OA=4.
∵四边形OCED是平行四边形,
∴OD=CE=4,OC=DE.
在Rt△DOE中,∠DOE=90°,OD=4,OE=2,
∴DE= ,
∴C平行四边形OCED=2(OD+DE)=2(4+2 )=8+4 .
②设点C的坐标为(x, +4),则CE=|x|,CD=| x+4|,
∴S△CDE= CD?CE=|﹣ x2+2x|= ,
∴x2+8x+33=0或x2+8x﹣33=0.
方程x2+8x+33=0无解;
解方程x2+8x﹣33=0,得:x1=﹣3,x2=11,
∴点C的坐标为(﹣3, )或(11, ).
【解析】【解答】(1)将A(8,0)代入y=kx+4,得:0=8k+4,
解得:k= .
故答案为: 。
【分析】(1)将点A的坐标代入直线y=kx+4(k≠0) 即可算出k的值,从而求出一次函数的解析式; (2) ① 根据直线与y轴交点的坐标特点,求出点B的坐标,从而得出OB的长度,根据中点的定义得出BE=OE=2,根据平行四边形的对边平行得出 CE∥DA, 根据平行线分线段成比例定理得出 ,所以点C是AB的中点, 进而根据三角形的中位线定理得出 CE= OA=4, 在Rt△DOE中 ,利用勾股定理算出DE长,从而根据平行四边形周长的计算方法即可算出答案; ② 根据点的坐标与图形的性质设出点C的坐标,然后根据三角形的面积计算方法,由 △CDE的面积为 建立方程,求解即可得出x的值,从而求出点C的坐标。
18.【答案】 B
【解析】【解答】解:如图,过O作 ,交AC于G,
∵O是BD的中点,
∴G是DC的中点.
又 ,
设 ,又 ,
,
故答案为:B.
【分析】如图,过O作 ,交AC于G,根据平行线分线段成比例可得出AD:DC=1:2,从而可得AD=DG=GC,AG:GC=2:1,AO:OE=2:1,由△AOB与△BOE同高,可得S△AOB:S△BOE=AO:OE=2:1,由同高不同底的三角形中底与三角形的面积关系即可BE:FC的比.21教育名师原创作品
同课章节目录
