4.3 相似三角形 同步练习(解析版)
图片预览



文档简介
初中数学浙教版九年级上册4.3 相似三角形 同步训练
一、基础夯实
1.如图,△ABC~△DEF,相似比为1:2.若BC=1,则EF的长是(??? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
2.若△ABC的每条边长增加各自的10%得△A'B'C',则∠B'的度数与其对应角∠B的度数相比(?? ?? ) A.?增加了10%????????????????????B.?减少了10%????????????????????C.?增加了(1+10%)????????????????????D.?没有变化
3.在△ABC和△DEF中,∠A=40°,∠D=60°,∠E=80°, ,那么∠B的度数是( ???)
A.?40°??????????????????????????????????????B.?60°??????????????????????????????????????C.?80°??????????????????????????????????????D.?100°
4.如图,已知△ABC,D,E分别是AB,AC边上的点.AD=3cm,AB=8cm,AC=10cm.若△ADE∽△ABC,则AE的值为( ??)www-2-1-cnjy-com
A.?cm????????????????????B.?cm或 cm????????????????????C.?cm或 cm????????????????????D.?cm
5.如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是(??? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
6.已知△ABC∽△A′B′C′且S△ABC:S△A′B′C′=1:2,则AB:A′B′=________. 【出处:21教育名师】
7.如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为________米. 21教育名师原创作品
8.如图中两三角形相似,则x=________.
9.△ABC的三边分别为 、 、2,△A′B′C′的两边长分别为2和2 ,如果△ABC∽△A′B′C′,那么△A′B′C′的第三边的长是________. 21*cnjy*com
10.如图,已知△AOB∽△DOC,OA=2,AD=9,OB=5,DC=12.求AB,OC的长.
二、强化提升
11.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为3cm, 和6m,另一个三角形的最长边长为12cm,则它的最短边长为 ??
A.?6cm???????????????????????????????????B.?9cm???????????????????????????????????C.?16cm???????????????????????????????????D.?24cm
12.一个三角形三边的长分别为3,4,5,另一个与它相似的三角形的最长边是10,则其他两边的和是(?? )
A.?9?????????????????????????????????????????B.?12?????????????????????????????????????????C.?13?????????????????????????????????????????D.?14
13.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为(??? )
A.?10米??????????????????????????????????B.?12米??????????????????????????????????C.?15米??????????????????????????????????D.?米
14.如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是(?? )
A.?AB2=BC?BD????????????????B.?AB2=AC?BD????????????????C.?AB?AD=BD?BC????????????????D.?AB?AD=AD?CD
15.如图,在△ABC中,点D,E分别在AB,AC上,且DE∥BC,AD=1,BD=2,那么 的值为(??? )
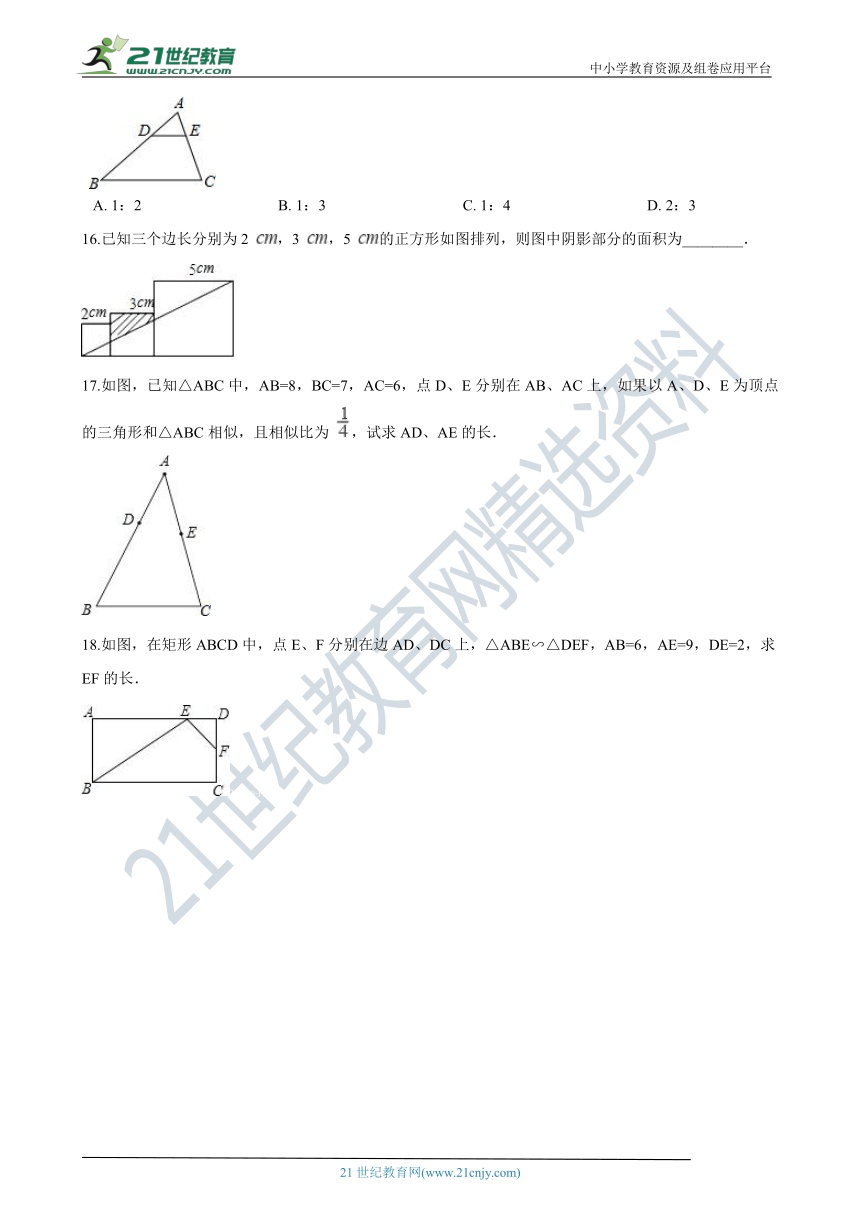
A.?1:2????????????????????????????????????B.?1:3????????????????????????????????????C.?1:4????????????????????????????????????D.?2:3
16.已知三个边长分别为2 ,3 ,5 的正方形如图排列,则图中阴影部分的面积为________.
17.如图,已知△ABC中,AB=8,BC=7,AC=6,点D、E分别在AB、AC上,如果以A、D、E为顶点的三角形和△ABC相似,且相似比为 ,试求AD、AE的长.
????
18.如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
2-1-c-n-j-y
答案解析部分
一、基础夯实
1.【答案】 B
解析:解: △ABC~△DEF, 相似比为1:2 ∴ 解之:EF=2 故答案为:B
根据相似三角形的性质及相似比为1:2 ,就可得到BC:EF=1:2,再求出EF的长。
2.【答案】 D
解析:【解答】三角形的各边都增加10%,则所得的三角形与原三角形相似,相似比为1.1∶1,相似三角形对应角相等。 故答案为:D。 三边扩大相同的比例,三边对应比相等,故前后三角形相似,相似三角形对应角相等,故角没有变化。
3.【答案】B
解析:解:∵ ,
∴∠B与∠D是对应角,
故∠B=∠D=60°.
故答案为:B.
根据题意,得知∠B与∠D为对应角,求出∠D的度数。
4.【答案】 A
解析:解:连接DE,
∵△ADE∽△ABC,
∴AD:AB=AE:AC
∴3:8=AE:10
∴AE=
故答案为:A.
连接DE,可证△ADE∽△ABC,通过对应边成比例,求出AE的长度。
5.【答案】 C
解析:解:∵△ABO∽△CDO,
∴ = ,
∵BO=6,DO=3,CD=2,
∴ = ,
解得:AB=4.
故答案为:C.
根据相似三角形对应边成比例得出 = ,根据比例式即可求出AB的长。
6.【答案】 1:
解析:∵△ABC∽△A′B′C′,
∴S△ABC:S△A′B′C′=AB2:A′B′2=1:2,
∴AB:A′B′=1: ,
故答案为:1: 根据相似三角形的面积比等于相似比的平方即可解答。
7.【答案】 1.4
解析:解:由题意得, ,
解得h=1.4.
故答案为:1.4.
根据相似三角形对应边成比例得出, 求解即可。
8.【答案】2
解析:解:由图形可得 = , 解得x=2. 故答案为:2. 相似三角形的对应边与对应角相等,求出x的值。21教育网
9.【答案】
解析:解:设△A′B′C′的第三边的长为x, ∵△ABC∽△A′B′C′, ∴ = = ,解得x=2 , 即△A′B′C′的第三边的长是2 . 故答案为2 . 根据相似三角形对应边成比例,求得第三边的长。
10.【答案】解:∵OA=2,AD=9, ∴OD=9﹣2=7, ∵△AOB∽△DOC, ∴ = = , ∵OA=2,OB=5,DC=12, ∴ = = ,解得OC= ,AB= . 21·世纪*教育网
解析:根据相似三角形的性质,对应边成比例,求得AB的值。
二、强化提升
11.【答案】 A
解析:解:设另一个三角形的最短边长为xcm,
根据题意,得: ,
解得: ,
即另一个三角形的最短边的长为6cm。
故答案为:A。
根据题意,两个三角形框架是相似的,根据相似三角形对应边成比例即可列出方程,求解即可。
12.【答案】 D
解析:设另一个三角形的最短边为x,第二短边为y,根据相似三角形的三边对应成比例,知 ,∴x=6,y=8,∴x+y=14.
故答案为:D.
根据相似三角形的对应边成比例,列出等式计算即得.
13.【答案】 A
解析:解:∵ =
即 = ,
∴楼高=10米.
故答案为:A
先根据相似三角形的判定证明两个三角形相似,然后根据同一时刻高与影长比例相同可得, 即可求出楼高.
14.【答案】 A
解析:∵ △ABC∽△DBA ,∴ ,∴ =BC·BD.
根据相似三角形对应边成比例得出,根据比例性质即可得出等积式。
15.【答案】 B
解析:解:∵DE∥BC,
∴△ADE∽△ABC,
∴ = ,
∵AD=1,DB=2,
∴ = ,
∴ = .
故答案为:B.
根据相似三角形的边长成比例,可解出此题比例的值。
16.【答案】
解析:解:如图,
对角线所分得的三个三角形相似,
根据相似的性质可知 ,
解得 ,
即阴影梯形的上底就是 ( ).
再根据相似的性质可知 ,
解得: ,
所以梯形的下底就是 ,
所以阴影梯形的面积是 .
故答案为: . 根据题意对角线所分得的三个三角形相似,对应边成比例,分析可求阴影部分梯形的上底和下底,即可求出梯形的面积。
17.【答案】解:当△ABC∽△ADE时,相似比为 , = = ,即: = = , 解得:AD=2,AE=1.5; 当△ABC∽△AED时, = = , 即: = = , 解得:AD=1.5,AE=2
解析:以A、D、E为顶点的三角形和△ABC相似,分两种情况讨论:当△ABC∽△ADE时;当△ABC∽△AED时。利用相似三角形的性质,分别得出对应边成比例,分别求出AD和AE的值即可解答。
18.【答案】解:∵四边形ABCD是矩形,∴∠BAE=90°, ∵AB=6,AE=9, ∴ , ∵△ABE∽△DEF, ∴ ,即 , 解得
解析:利用矩形的性质及勾股定理求出BE的长,再利用相似三角形的性质,得出对应边成比例,将相关的线段代入可求解。:21教育】
一、基础夯实
1.如图,△ABC~△DEF,相似比为1:2.若BC=1,则EF的长是(??? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
2.若△ABC的每条边长增加各自的10%得△A'B'C',则∠B'的度数与其对应角∠B的度数相比(?? ?? ) A.?增加了10%????????????????????B.?减少了10%????????????????????C.?增加了(1+10%)????????????????????D.?没有变化
3.在△ABC和△DEF中,∠A=40°,∠D=60°,∠E=80°, ,那么∠B的度数是( ???)
A.?40°??????????????????????????????????????B.?60°??????????????????????????????????????C.?80°??????????????????????????????????????D.?100°
4.如图,已知△ABC,D,E分别是AB,AC边上的点.AD=3cm,AB=8cm,AC=10cm.若△ADE∽△ABC,则AE的值为( ??)www-2-1-cnjy-com
A.?cm????????????????????B.?cm或 cm????????????????????C.?cm或 cm????????????????????D.?cm
5.如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是(??? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
6.已知△ABC∽△A′B′C′且S△ABC:S△A′B′C′=1:2,则AB:A′B′=________. 【出处:21教育名师】
7.如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为________米. 21教育名师原创作品
8.如图中两三角形相似,则x=________.
9.△ABC的三边分别为 、 、2,△A′B′C′的两边长分别为2和2 ,如果△ABC∽△A′B′C′,那么△A′B′C′的第三边的长是________. 21*cnjy*com
10.如图,已知△AOB∽△DOC,OA=2,AD=9,OB=5,DC=12.求AB,OC的长.
二、强化提升
11.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为3cm, 和6m,另一个三角形的最长边长为12cm,则它的最短边长为 ??
A.?6cm???????????????????????????????????B.?9cm???????????????????????????????????C.?16cm???????????????????????????????????D.?24cm
12.一个三角形三边的长分别为3,4,5,另一个与它相似的三角形的最长边是10,则其他两边的和是(?? )
A.?9?????????????????????????????????????????B.?12?????????????????????????????????????????C.?13?????????????????????????????????????????D.?14
13.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为(??? )
A.?10米??????????????????????????????????B.?12米??????????????????????????????????C.?15米??????????????????????????????????D.?米
14.如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是(?? )
A.?AB2=BC?BD????????????????B.?AB2=AC?BD????????????????C.?AB?AD=BD?BC????????????????D.?AB?AD=AD?CD
15.如图,在△ABC中,点D,E分别在AB,AC上,且DE∥BC,AD=1,BD=2,那么 的值为(??? )
A.?1:2????????????????????????????????????B.?1:3????????????????????????????????????C.?1:4????????????????????????????????????D.?2:3
16.已知三个边长分别为2 ,3 ,5 的正方形如图排列,则图中阴影部分的面积为________.
17.如图,已知△ABC中,AB=8,BC=7,AC=6,点D、E分别在AB、AC上,如果以A、D、E为顶点的三角形和△ABC相似,且相似比为 ,试求AD、AE的长.
????
18.如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
2-1-c-n-j-y
答案解析部分
一、基础夯实
1.【答案】 B
解析:解: △ABC~△DEF, 相似比为1:2 ∴ 解之:EF=2 故答案为:B
根据相似三角形的性质及相似比为1:2 ,就可得到BC:EF=1:2,再求出EF的长。
2.【答案】 D
解析:【解答】三角形的各边都增加10%,则所得的三角形与原三角形相似,相似比为1.1∶1,相似三角形对应角相等。 故答案为:D。 三边扩大相同的比例,三边对应比相等,故前后三角形相似,相似三角形对应角相等,故角没有变化。
3.【答案】B
解析:解:∵ ,
∴∠B与∠D是对应角,
故∠B=∠D=60°.
故答案为:B.
根据题意,得知∠B与∠D为对应角,求出∠D的度数。
4.【答案】 A
解析:解:连接DE,
∵△ADE∽△ABC,
∴AD:AB=AE:AC
∴3:8=AE:10
∴AE=
故答案为:A.
连接DE,可证△ADE∽△ABC,通过对应边成比例,求出AE的长度。
5.【答案】 C
解析:解:∵△ABO∽△CDO,
∴ = ,
∵BO=6,DO=3,CD=2,
∴ = ,
解得:AB=4.
故答案为:C.
根据相似三角形对应边成比例得出 = ,根据比例式即可求出AB的长。
6.【答案】 1:
解析:∵△ABC∽△A′B′C′,
∴S△ABC:S△A′B′C′=AB2:A′B′2=1:2,
∴AB:A′B′=1: ,
故答案为:1: 根据相似三角形的面积比等于相似比的平方即可解答。
7.【答案】 1.4
解析:解:由题意得, ,
解得h=1.4.
故答案为:1.4.
根据相似三角形对应边成比例得出, 求解即可。
8.【答案】2
解析:解:由图形可得 = , 解得x=2. 故答案为:2. 相似三角形的对应边与对应角相等,求出x的值。21教育网
9.【答案】
解析:解:设△A′B′C′的第三边的长为x, ∵△ABC∽△A′B′C′, ∴ = = ,解得x=2 , 即△A′B′C′的第三边的长是2 . 故答案为2 . 根据相似三角形对应边成比例,求得第三边的长。
10.【答案】解:∵OA=2,AD=9, ∴OD=9﹣2=7, ∵△AOB∽△DOC, ∴ = = , ∵OA=2,OB=5,DC=12, ∴ = = ,解得OC= ,AB= . 21·世纪*教育网
解析:根据相似三角形的性质,对应边成比例,求得AB的值。
二、强化提升
11.【答案】 A
解析:解:设另一个三角形的最短边长为xcm,
根据题意,得: ,
解得: ,
即另一个三角形的最短边的长为6cm。
故答案为:A。
根据题意,两个三角形框架是相似的,根据相似三角形对应边成比例即可列出方程,求解即可。
12.【答案】 D
解析:设另一个三角形的最短边为x,第二短边为y,根据相似三角形的三边对应成比例,知 ,∴x=6,y=8,∴x+y=14.
故答案为:D.
根据相似三角形的对应边成比例,列出等式计算即得.
13.【答案】 A
解析:解:∵ =
即 = ,
∴楼高=10米.
故答案为:A
先根据相似三角形的判定证明两个三角形相似,然后根据同一时刻高与影长比例相同可得, 即可求出楼高.
14.【答案】 A
解析:∵ △ABC∽△DBA ,∴ ,∴ =BC·BD.
根据相似三角形对应边成比例得出,根据比例性质即可得出等积式。
15.【答案】 B
解析:解:∵DE∥BC,
∴△ADE∽△ABC,
∴ = ,
∵AD=1,DB=2,
∴ = ,
∴ = .
故答案为:B.
根据相似三角形的边长成比例,可解出此题比例的值。
16.【答案】
解析:解:如图,
对角线所分得的三个三角形相似,
根据相似的性质可知 ,
解得 ,
即阴影梯形的上底就是 ( ).
再根据相似的性质可知 ,
解得: ,
所以梯形的下底就是 ,
所以阴影梯形的面积是 .
故答案为: . 根据题意对角线所分得的三个三角形相似,对应边成比例,分析可求阴影部分梯形的上底和下底,即可求出梯形的面积。
17.【答案】解:当△ABC∽△ADE时,相似比为 , = = ,即: = = , 解得:AD=2,AE=1.5; 当△ABC∽△AED时, = = , 即: = = , 解得:AD=1.5,AE=2
解析:以A、D、E为顶点的三角形和△ABC相似,分两种情况讨论:当△ABC∽△ADE时;当△ABC∽△AED时。利用相似三角形的性质,分别得出对应边成比例,分别求出AD和AE的值即可解答。
18.【答案】解:∵四边形ABCD是矩形,∴∠BAE=90°, ∵AB=6,AE=9, ∴ , ∵△ABE∽△DEF, ∴ ,即 , 解得
解析:利用矩形的性质及勾股定理求出BE的长,再利用相似三角形的性质,得出对应边成比例,将相关的线段代入可求解。:21教育】
同课章节目录
