4.6 相似多边形 同步练习（解析版）

初中数学浙教版九年级上册4.6 相似多边形 基础巩固训练
一、单选题
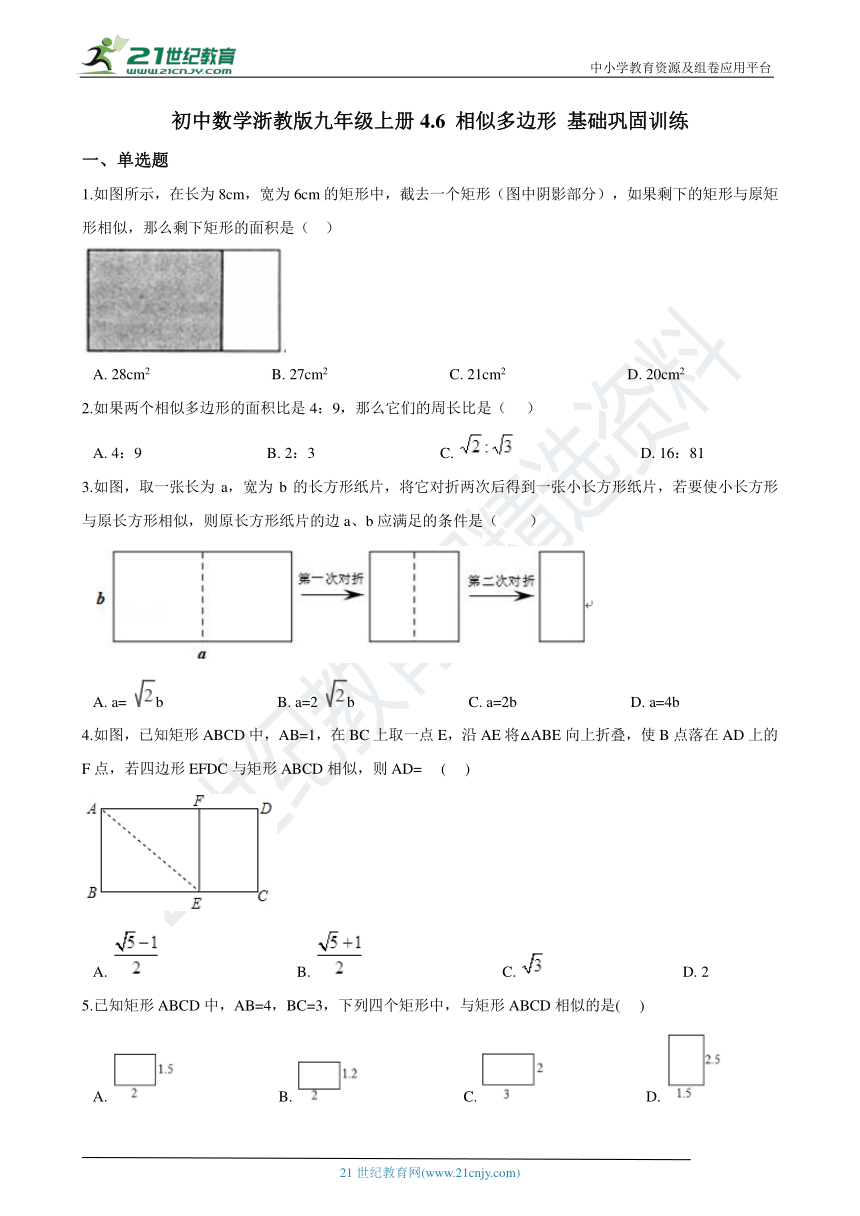
1.如图所示，在长为8cm，宽为6cm的矩形中，截去一个矩形（图中阴影部分），如果剩下的矩形与原矩形相似，那么剩下矩形的面积是（?? ）
A.?28cm2????????????????????????????????B.?27cm2????????????????????????????????C.?21cm2????????????????????????????????D.?20cm2
2.如果两个相似多边形的面积比是4：9，那么它们的周长比是（??? ）
A.?4：9?????????????????????????????????B.?2：3?????????????????????????????????C.??????????????????????????????????D.?16：81
3.如图，取一张长为a，宽为b的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边a、b应满足的条件是（?? ）
A.?a= b??????????????????????????????B.?a=2 b??????????????????????????????C.?a=2b??????????????????????????????D.?a=4b
4.如图，已知矩形ABCD中，AB=1，在BC上取一点E，沿AE将△ABE向上折叠，使B点落在AD上的F点，若四边形EFDC与矩形ABCD相似，则AD=??? (??? )
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?2
5.已知矩形ABCD中，AB=4，BC=3，下列四个矩形中，与矩形ABCD相似的是(??? )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
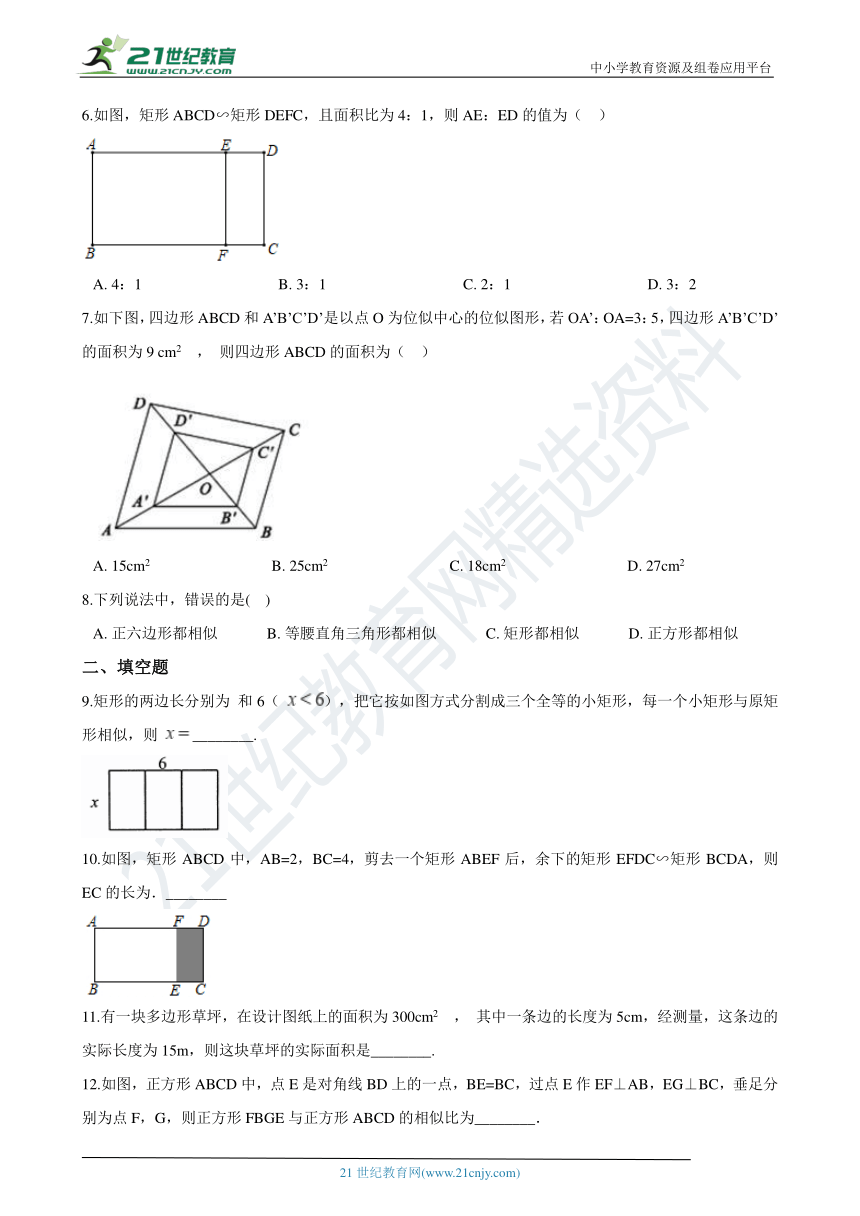
6.如图，矩形ABCD∽矩形DEFC，且面积比为4：1，则AE：ED的值为（?? ）
A.?4：1????????????????????????????????????B.?3：1????????????????????????????????????C.?2：1????????????????????????????????????D.?3：2
7.如下图，四边形ABCD和A’B’C’D’是以点O为位似中心的位似图形，若OA’：OA=3：5，四边形A’B’C’D’的面积为9 cm2 ， 则四边形ABCD的面积为（ ??）
A.?15cm2????????????????????????????????B.?25cm2????????????????????????????????C.?18cm2????????????????????????????????D.?27cm2
8.下列说法中，错误的是( ??)
A.?正六边形都相似?????????????B.?等腰直角三角形都相似?????????????C.?矩形都相似?????????????D.?正方形都相似
二、填空题
9.矩形的两边长分别为 和6（ ），把它按如图方式分割成三个全等的小矩形，每一个小矩形与原矩形相似，则 ________.
10.如图，矩形ABCD中，AB=2，BC=4，剪去一个矩形ABEF后，余下的矩形EFDC∽矩形BCDA，则EC的长为．________
11.有一块多边形草坪，在设计图纸上的面积为300cm2 ， 其中一条边的长度为5cm，经测量，这条边的实际长度为15m，则这块草坪的实际面积是________.
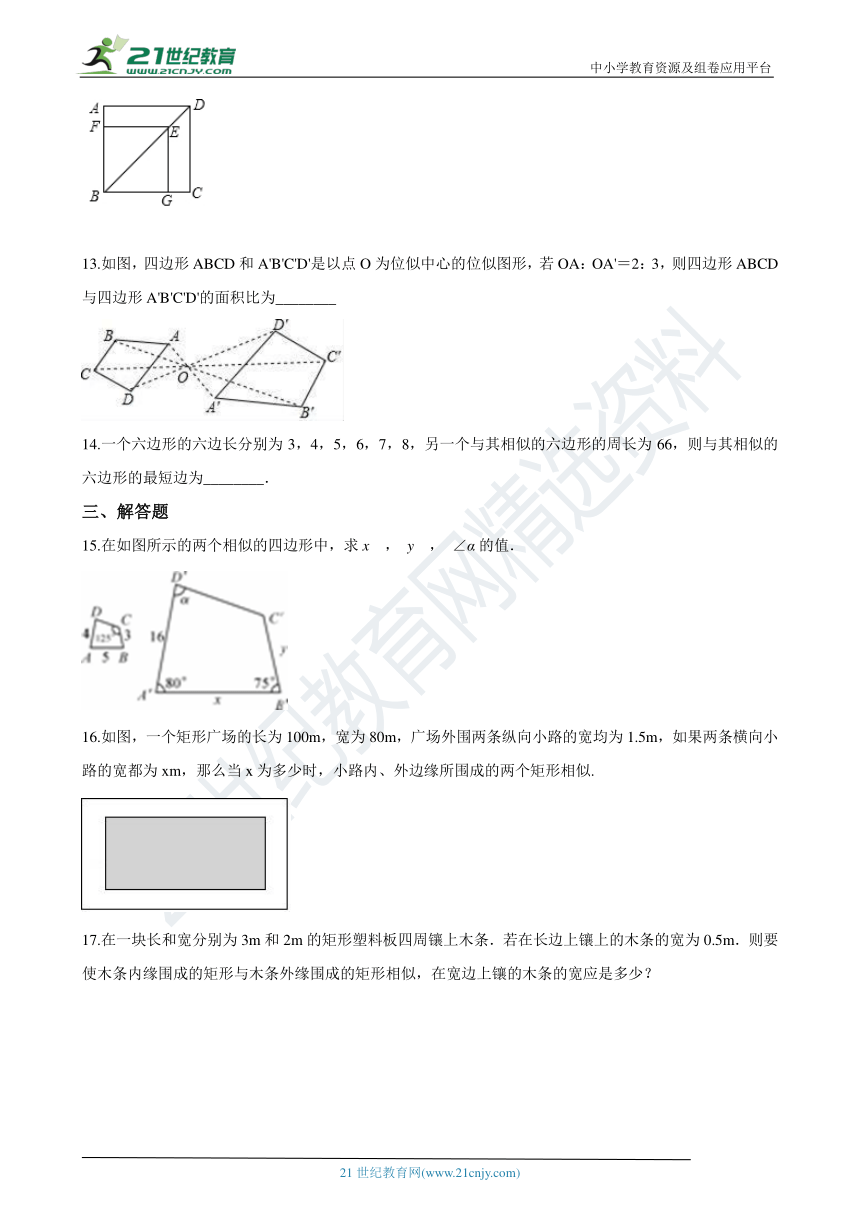
12.如图，正方形ABCD中，点E是对角线BD上的一点，BE=BC，过点E作EF⊥AB，EG⊥BC，垂足分别为点F，G，则正方形FBGE与正方形ABCD的相似比为________．

13.如图，四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形，若OA：OA'＝2：3，则四边形ABCD与四边形A'B'C'D'的面积比为________
14.一个六边形的六边长分别为3，4，5，6，7，8，另一个与其相似的六边形的周长为66，则与其相似的六边形的最短边为________．
三、解答题
15.在如图所示的两个相似的四边形中，求x ， y ， ∠α的值．
16.如图，一个矩形广场的长为100m，宽为80m，广场外围两条纵向小路的宽均为1.5m，如果两条横向小路的宽都为xm，那么当x为多少时，小路内、外边缘所围成的两个矩形相似.
17.在一块长和宽分别为3m和2m的矩形塑料板四周镶上木条．若在长边上镶上的木条的宽为0.5m．则要使木条内缘围成的矩形与木条外缘围成的矩形相似，在宽边上镶的木条的宽应是多少？
18.图中的两个多边形ABCDEF和A1B1C1D1E1F1相似(各字母已按对应关系排列)，∠A＝∠D1＝135°，∠B＝∠E1＝120°，∠C1＝95°.
（1）求∠F的度数；
（2）如果多边形ABCDEF和A1B1C1D1E1F1的相似比是1：1.5，且CD＝15cm，求C1D1的长度．
答案解析部分
一、单选题
1.【答案】 B
解析：解：如图， 依题意，在矩形ABDC中截取矩形ABFE，
则矩形ABDC∽矩形FDCE，
则 AE/DF=BD/DC
设DF=xcm，得到：6/x=8/6
解得：x=4.5，
则剩下的矩形面积是：4.5×6=27cm2 ． 根据相似多边形的对应边相等，得出 ,根据比例式建立方程，求解即可。
2.【答案】 B
解析：相似多边形的面积比等于相似比的平方，故相似多边形的相似比为2∶3，相似多边形周长比等于相似比。 故答案为：B。 由相似多边形的性质：相似多边形的面积比等于相似比的平方，周长比等于相似比可得。
3.【答案】 C
解析：解：由题干可知，对折两次后的小长方形纸片的长为b，宽为 ，为了使小长方形与原长方形相似，由相似的性质有 化简整理得a=2b。故答案为：C。
根据对折的性质可知：对折两次后的小长方形纸片的长为b，宽为 ， 根据相似多边形的对应边成比例得出整理即可得出答案。
4.【答案】 B
解析：解：∵AB=1， 设AD=x，则FD=x?1，FE=1， ∵四边形EFDC与矩形ABCD相似， ∴ ∴ 解之：x1=， x2=(不合题意舍去)， 经检验xx1=是原方程的解。 故答案为：B
设AD=x，由四边形EFDC与矩形ABCD相似，根据相似多边形对应边的比相等列出比例式，建立关于x的方程，解方程求出x的值，即可得到AD的长。
5.【答案】 A
解析：矩形ABCD的长宽之比为4∶3, A、长宽之比为2∶1.5=4∶3，A符合题意； B、长宽之比为2:1.2=5:3，B不符合题意； C、长宽之比为3:2，C不符合题意； D、长宽之比为2.5∶1.5=5∶3，D不符合题意； 故答案为：A 分别把每个矩形的长宽之比化为最简整数比，比较即可。
6.【答案】 B
解析：解： 矩形ABCD∽矩形DEFC，且面积比为4：1，
： ：1，
设 ， ，
，
则 ，
整理，得： ，
则 ，即AE： ：1。
故答案为：B。
根据相似多边形面积的比等于相似比的平方得出： ：1， 设 ， ，根据矩形的性质得出， 根据矩形的面积计算方法，由 矩形ABCD与矩形DEFC面积比为4：1 列出方程，求解用含a的式子表示出x，进而即可求出答案。
7.【答案】 B
解析：∵ 四边形ABCD和四边形A’B’C’D’是以点O为位似中心的位似图形， ∴ ∴ 解之：S四边形ABCD=25 故答案为：B
根据已知条件：四边形ABCD和四边形A’B’C’D’是以点O为位似中心的位似图形，就可得到这两个四边形是相似形，利用相似多边形的性质：相似多边形的面积比等于相似比的平方，就可求出四边形ABCD的面积。
8.【答案】 C
解析：A.所有的正六边形的对应角相等，对应边的比相等，符合相似的定义，故符合题意，不符合题意；
B.所有的等腰直角三角形的对应角相等，对应边的比相等，符合相似的定义，故符合题意，不符合题意；
C.矩形的对应边的比不一定相等，故不符合相似的定义，符合题意；
D.正方形的对应角相等，对应边的比相等，符合相似的定义，故符合题意，不符合题意，
故答案为：C. 根据相似三角形的判定和相似多边形的定义解答
二、填空题
9.【答案】
解析：解：∵原矩形ABCD的长为6，宽为x，
∴小矩形的长为x，宽为 =2，
∵小矩形与原矩形相似，
∴
∴x=2 .
故答案为：2 .
由相似图形的性质可得比例式求解。
10.【答案】 1
解析： 解：∵矩形EFDC∽矩形BCDA ∴ ∴EF=AB ∴ 解之：EC=1 故答案为：1
利用已知矩形EFDC∽矩形BCDA，可证得对应边成比例，即， 然后代入相关线段的长，就可求出EC的长。
11.【答案】 2700m2
解析：解：设草坪的实际面积是 ，因为地图图形与实际图形相似，所以方程为：
，解得 ,经检验， 是方程的解.
故答案为： . 由题意知地图图形与实际图形相似，所以根据相似形的性质“相似图形的面积的比等于相似比”可求解。
12.【答案】
解析：解：设BG=x，
则BE= x，
∵BE=BC，
∴BC= x，
则正方形FBGE与正方形ABCD的相似比=BG：BC=x： x= ：2，
故答案为：
设BG=x，可得BE= x，BC= x，可得两个正方形的相似比.
13.【答案】 4：9
解析：解：∵四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形，OA：OA'＝2：3，
∴四边形ABCD与四边形A'B'C'D'的面积比4：9，
故答案为：4：9．
根据四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形，它的面积之比为边长比的平方，据此解答即可。
14.【答案】6
解析：解：设另一个六边形的最短边的长为x，
根据题意得 = ，
解得x=6，
即另一个六边形的最短边的长为6．
故答案为6
利用相似多边形的周长比等于相似比，建立关于x的方程，求解即可。
三、解答题
15.【答案】 解:∵四边形ABCD∽四边形A′B′C′D′，
∴ ，∠C′=∠C=125°，
即 ，
∴x=20，y=12，
在四边形A′B′C′D′，α=360°-∠A′-∠B′-∠C′=360°-80°-75°-125°=80°.
解析：根据相似多边形对应角相等可得 ∠C′=∠C=125° ，再由四边形内角和求出 ∠α?；再根据相似多边形对应边成比例计算即可
16.【答案】 解：当 时，小路内、外边缘所围成的两个矩形相似.
解得x=1.2
答：当x为1.2m时，小路内、外边缘所围成的两个矩形相似.
解析：根据两个矩形相似可得比例式，于是可列方程求解。
17.【答案】解：设在宽边上镶的木条的宽应是xm，根据题意，得
= ，
解得x=0.75．
答：在宽边上镶的木条的宽应是0.75m
解析：【分析】根据题意可证得两矩形相似，且相似比为3:2，设在宽边上镶的木条的宽应是xm，利用相似多边形的对应边成比例，列出关于x的方程求解即可。
18.【答案】（1）解：∵多边形ABCDEF和A1B1C1D1E1F1相似，∠A＝∠D1＝135°，∠B＝∠E1＝120°，∠C1＝95°，
∴∠C＝∠C1＝95°，∠D＝∠D1＝135°，∠E＝∠E1＝120°.
由多边形内角和定理，得多边形ABCDEF的内角和为180°×(6－2)＝720°，
∴∠F＝720°－(135°＋120°＋95°＋135°＋120°)＝115°（2）解：∵多边形ABCDEF和A1B1C1D1E1F1的相似比是1：1.5，且CD＝15cm，
∴C1D1＝15×1.5＝22.5(cm)．
解析：（1）由相似多边形的对应角相等和已知条件可得∠C＝∠C1＝95°，∠D＝∠D1＝135°，∠E＝∠E1＝120°，再根据多边形内角和=（n-2）=（6-2），用求得的六边形的内角和减去已知的角的度数即为∠F的度数；（2）根据相似多边形的对应边的比等于相似比即可求解。