4.7 图形的位似 强化练习(解析版)
图片预览



文档简介
初中数学浙教版九年级上册4.7 图形的位似 强化提升训练
一、单选题
1.如图所示,△OAB与△OCD是以点O为位似中心的位似图形,位似比为1:2,∠OCD=90°,CO=CD.若OB=1,则点C的坐标为(?? ) 21教育网
A.?(﹣1,2)??????????????????B.?( , )??????????????????C.?(﹣1,1)??????????????????D.?(1.﹣1)
2.如图,在平面直角坐标系中有两点A(6,2),B(6,0),以原点为位似中心,相似比为3∶1,把线段AB缩小得到A′B′,则过A′点对应点的反比例函数的解析式为(??? )www.21-cn-jy.com
A.?y= ??????????????????????????????B.?y= ??????????????????????????????C.?y=- ??????????????????????????????D.?y=
3.如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是(?? )【来源:21·世纪·教育·网】
A.?(4,2)???????????????????????????B.?(4,1)???????????????????????????C.?(5,2)???????????????????????????D.?(5,1)
4.在研究位似问题时,甲、乙同学的说法如下:
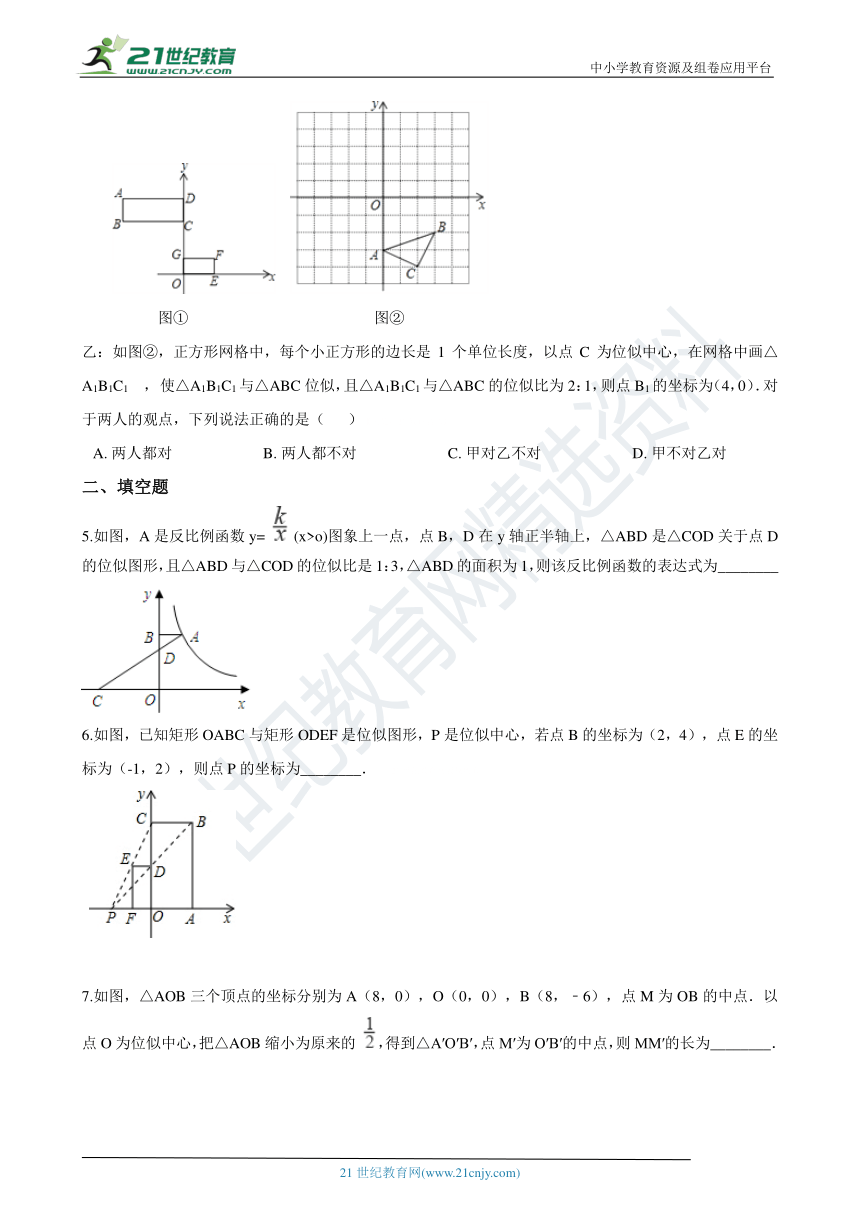
甲:如图①,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为(0,2).【来源:21cnj*y.co*m】
??
图①??????????????????????? 图②
乙:如图②,正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画△A1B1C1 , 使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,则点B1的坐标为(4,0).对于两人的观点,下列说法正确的是(???? )【出处:21教育名师】
A.?两人都对????????????????????????B.?两人都不对????????????????????????C.?甲对乙不对????????????????????????D.?甲不对乙对
二、填空题
5.如图,A是反比例函数y= ?(x>o)图象上一点,点B,D在y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3,△ABD的面积为1,则该反比例函数的表达式为________
6.如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为________. 21世纪教育网版权所有
7.如图,△AOB三个顶点的坐标分别为A(8,0),O(0,0),B(8,﹣6),点M为OB的中点.以点O为位似中心,把△AOB缩小为原来的 ,得到△A′O′B′,点M′为O′B′的中点,则MM′的长为________. 【版权所有:21教育】
8.如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为 ,点E的坐标为 ,则点P的坐标为________. 21cnjy.com
9.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是________.21*cnjy*com
10.如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1 , 其边长OA1缩小为OA的 ,经第二次变化后得正方形OA2B2C2 , 其边长OA2缩小为OA1的 ,经第三次变化后得正方形OA3B3C3 , 其边长OA3缩小为OA2的 ,…,依次规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=________.
三、综合题
11.在平面直角坐标系 中,已知 和 的顶点坐标分别为 、 、 、 、 、 .
按下列要求画图:以点 为位似中心,将 向 轴左侧按比例尺 放大得 的位似图形 ,并解决下列问题:
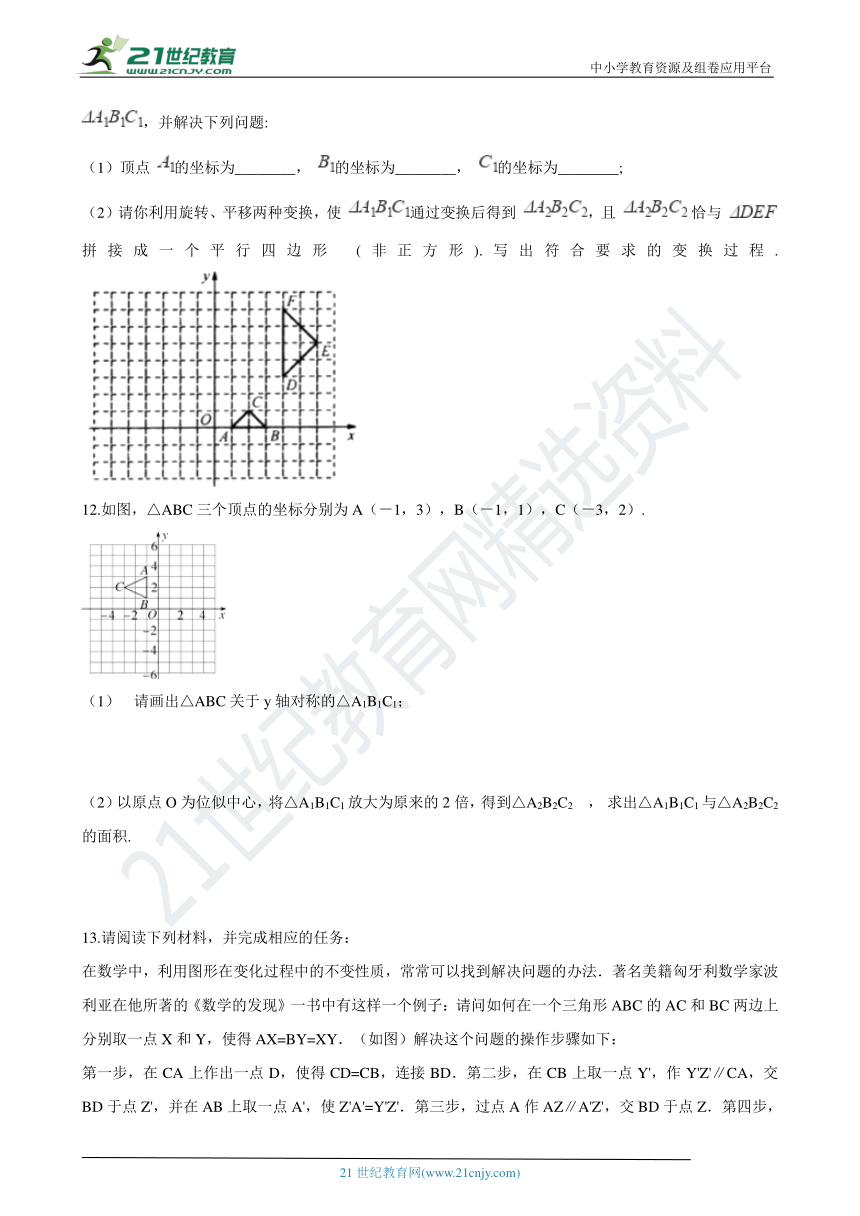
(1)顶点 的坐标为________, 的坐标为________, 的坐标为________;
(2)请你利用旋转、平移两种变换,使 通过变换后得到 ,且 ?恰与 拼接成一个平行四边形 (非正方形).写出符合要求的变换过程.
12.如图,△ABC三个顶点的坐标分别为A(-1,3),B(-1,1),C(-3,2).
请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2 , 求出△A1B1C1与△A2B2C2的面积.
13.请阅读下列材料,并完成相应的任务:
在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办法.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y,使得AX=BY=XY.(如图)解决这个问题的操作步骤如下:
第一步,在CA上作出一点D,使得CD=CB,连接BD.第二步,在CB上取一点Y',作Y'Z'∥CA,交BD于点Z',并在AB上取一点A',使Z'A'=Y'Z'.第三步,过点A作AZ∥A'Z',交BD于点Z.第四步,过点Z作ZY∥AC,交BC于点Y,再过点Y作YX∥ZA,交AC于点X.
则有AX=BY=XY.
下面是该结论的部分证明:
证明:∵AZ∥A'Z',∴∠BA'Z'=∠BAZ,
又∵∠A'BZ'=∠ABZ.∴△BA'Z'~△BAZ.
∴ ?.
同理可得 .∴ .
∵Z'A'=Y'Z',∴ZA=YZ.
任务:
(1)请根据上面的操作步骤及部分证明过程,判断四边形AXYZ的形状,并加以证明;
(2)请再仔细阅读上面的操作步骤,在(1)的基础上完成AX=BY=XY的证明过程;?
(3)上述解决问题的过程中,通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY,从而确定了点Z,Y的位置,这里运用了下面一种图形的变化是?? ?????? .
A.?平移????????????????????????????????????B.?旋转????????????????????????????????????C.?轴对称????????????????????????????????????D.?位似
答案解析部分
一、单选题
1.【答案】 C
解析:解:连接BC,
∵△OAB∽△OCD,相似比为1:2,
∴ ,
∵OB=1,
∴OD=2,
∴BD=OB,
∵CD=CO,
∴CB⊥OD,
∴BC=DB=OB=1,
∴C(-1,1),
故答案为:C.
连接BC,由位似比为1:2 可得OB与OD的比为 1:2 ,由OB=1,可得OD=2,由等腰三角形的三线合一可得BC=DB=OB=1,即可得出点C的坐标。
2.【答案】 B
解析:解:∵△A1B1O和△ABO以原点为位似中心,
∴△A1B1O∽△ABO,相似比为3:1,
∴A1B1= ,OB1=2,
∴A1的坐标为(2, )或(﹣2,﹣ ),
设过此点的反比例函数解析式为y= ,则k= ,
所以解析式为y= .
故答案为:B.
A点关于点O的位似点有两种情况,一种是在第一象限,一种是在第三象限,设出过点A1的反比例函数的解析式,将点坐标代入,得出k的值,最后得出相应的反比例函数解析式。
3.【答案】 C
解析:分别过C,D,A,B,做x轴的垂线,垂足分别是F,H,K;因为A,D的横坐标相同,所以D在AH上,∵E(1,0),C(2,2),A(3,4),D(3,1),∴EF=1,FH=1;∵CF∥AH∥BK,∴ ,∵CD∥AB,∴ ,∵DH∥BK,∴ ,∵EH=2,DH=1,∴EK=4,BK=2,∴OK=5,∴B(5,2),故答案为:C.2·1·c·n·j·y
分别过C,D,A,B,做x轴的垂线,垂足分别是F,H,K;根据位似图形对应线段的比等于相似比即可求得对应线段的比值,根据位似图形对应边互相平行或在同一直线上可得CD∥AB;再根据平行线分线段成比例定理可求解。
4.【答案】 A
解析:解:∵矩形ABCD和矩形EFGO 是位似图形,∴B和F是对应点,设直线BF为y=kx+b,则 ,解得: ?,∴ .∵位似中心是直线BF和CG的交点,∴x=0,∴y=2,∴位似中心为P(0,2),故甲正确;
由图可知,点B的坐标为(3,﹣2),以点C为位似中心,在网格中画△A1B1C1 , 使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,则点B1的坐标为(5,0),故乙正确.
故答案为:A.
位似图形是指对应顶点的连线相交于一点的两个相似多边形。甲:根据定义易知B和F是对应点,用待定系数法可求得BF的解析式,直线BF与y轴的交点的坐标即为位似中心P的坐标;乙:根据位似图形的定义和已知条件可知,即为直线CB与x轴的交点,用待定系数法可求得直线CB的坐标,再求出直线CB与x轴的交点坐标即可。
二、填空题
5.【答案】
解析:解:过A作AE⊥x轴 ∵△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似是1:3, ∴ ∴OE=AB, ∴ ∵OD∥AE ∴△COD∽△CEA ∴ 设BD=x,AB=y ∴DO=3x,AE=4x,CO=3y, ∵△ABD的面积为1, ∴xy=1, ∴xy=2, ∴AB?AE=4xy=8, 该反比例函数的表达式为:y= 故答案为:y=y=
过A作AE⊥x轴,根据位似的性质及OE=AB,可证得, 再证明△COD∽△CEA,得出对应成比例,就可证得, 设BD=x,AB=y,分别表示出DO、AE、CO,然后根据 △ABD的面积为1 ,求出xy的值,从而可求出AB?AE的值,根据反比例函数的几何意义,就可得到函数解析式。
6.【答案】 (-2,0)
解析:解:∵四边形OABC是矩形,点B的坐标为(2,4),
∴OC=AB=4,OA=2,
∴点C的坐标为:(0,4),
∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点E的坐标为(-1,2),
∴位似比为1:2,
∴OP:AP=OD:AB=1:2,
设OP=x,则 ,
解得:x=2,
∴OP=2,
即点P的坐标为:(-2,0).
故答案为:(-2,0)
位似图形对应点连线相交于位似中心,可确定位似比为1:2,再根据OP:AP=OD:AB即可求得OP长,即可写出P点坐标。
7.【答案】或
解析:解:如图,在Rt△AOB中,OB= =10, ∴OM=5,OM′= , ①当△A′OB′在第三象限时,MM′=5- = ; ②当△A″OB″在第二象限时,MM′=5+ = , 故答案为: 或 . 以O点为位似中心,作三个对应点的坐标,存在于第二象限和第四象限,根据存在的两种情况,可得出MM′的长度。
8.【答案】(-2,0)
解析:解:∵四边形OABC是矩形,点B的坐标为(2,4), ∴OC=AB=4,OA=2, ∴点C的坐标为:(0,4), ∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点E的坐标为(-1,2), ∴位似比为:2, ∴OP:AP=OD:AB=1:2, 设OP=x,则 ,解得:x=2, ∴OP=2, 即点P的坐标为:(-2,0) 故答案为:(-2,0) 由B点坐标,可求C点坐标,继而求出两个矩形的位似比,可简单利用三角形相似、对应边成比例来求得点P的坐标。
9.【答案】(2,2 )
解析:解:分别过A作AE⊥OB,CF⊥OB, ∵∠OCD=90°,∠AOB=60°, ∴∠ABO=∠CDO=30°,∠OCF=30°, ∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,点B的坐标是(6,0), ∴D(8,0),则DO=8, 故OC=4, 则FO=2,CF=CO?cos30°=4× =2 , 故点C的坐标是:(2,2 ). 故答案为:(2,2 ). 分别过A作AE⊥OB,CF⊥OB,利用∠OCD=90°,∠AOB=60°,可求出∠ABO=∠CDO=30°,∠OCF=30°,再根据已知:△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,点B的坐标是(6,0),求出DO、OC、OF的长,然后利用解直角三角形求出CF的长,就可得出点C的坐标。
10.【答案】16
解析:由已知有:OA1= OA;OA2= OA1= OA,OA3= OA2= OA,......,∴OAn= OA, OAn= OA= ,∴ = ,∴n=16.故答案为:16. 由题意和图形可得OAn=OA=,将OA的值代入计算即可求解。
三、综合题
11.【答案】(1)(﹣2,0);(﹣6,0);(﹣4,﹣2) (2)解:如图,把△A1B1C1绕点O顺时针旋转90°,再向右平移6个单位,向下平移1个单位,使B2C2与DE重合,或者:把△A1B1C1绕点O顺时针旋转90°,再向右平移6个单位,向上平移3个单位,使A2C2与EF重合,都可以拼成一个平行四边形.
解析:解:(1)如图所示,△A1B1C1即为所求作的三角形,A1(﹣2,0)B1(﹣6,0)C1(﹣4,﹣2);
(1)延长AO到A1 , 使A1O=2AO,延长BO到B1,使B1O=2BO,连接CO并延长到C1 , 使C1O=2CO,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标即可。 (2)先绕点O顺时针旋转90°,然后向右平移再向下(或向上)平移,使△A2B2C2的直角边与△DEF的直角边重合即可。
12.【答案】(1)解:如图所示,△A1B1C1即为所求,
(2)解:由题图得S△A1B1C1= ×2×2=2.∵将△A1B1C1放大为原来的2倍,得到△A2B2C2 , ∴△A1B1C1∽△A2B2C2 , ∴ = ,∴ = = ,
∴S△A2B2C2=4S△A1B1C1=4×2=8.
即S△A1B1C1=2,S△A2B2C2=8.
解析:【分析】(1)根据关于y轴对称的点横坐标互为相反数,纵坐标不变求出A,B,C三点的对称点A1,B1,C1三点的坐标,利用方格纸的特点描出A1,B1,C1三点,再顺次连接即可; (2)连接A1O并延长,在其延长线上取点A2 , 使OA2=2OA1 , 同理作出B2,C2,再顺次连接即可得到△A2B2C2,首先算出△A1B1C1的面积,由位似的性质知△A1B1C1∽△A2B2C2,根据相似三角形面积的比等于相似比的平方即可得出△A2B2C2的面积。
13.【答案】(1)解:四边形AXYZ是菱形.
证明:∵ZY∥AC,YX∥ZA,
∴四边形AXYZ是平行四边形.
∵ZA=YZ,
∴平行四边形AXYZ是菱形 (2)证明:∵CD=CB,
∴∠1=∠3.
∵ZY∥AC,
∴∠1=∠2.
∴∠2=∠3.
∴YB=YZ.
∵四边形AXYZ是菱形,
∴AX=XY=YZ.
∴AX=BY=XY (3)D
解析:解:(3)通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY,从而确定了点Z,Y的位置,此时四边形BA'Z'Y'∽四边形BAZY,所以该变换形式是位似变换.故答案是:D(或位似).
(1)四边形AXYZ是菱形.理由如下:根据两组对边分别平行的四边形是平行四边形,由ZY∥AC,YX∥ZA,得出四边形AXYZ是平行四边形,根据有一组邻边相等的平行四边形是菱形,由四边形AXYZ是平行四边形及ZA=YZ,得出结论:平行四边形AXYZ是菱形; (2)根据等边对等角,由CD=CB,得出∠1=∠3,由二直线平行同位角相等得出∠1=∠2,故∠2=∠3,根据等角对等边得出YB=YZ,根据菱形的性质得出∴AX=XY=YZ,从而得出结论; (3)通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY,从而确定了点Z,Y的位置,运用的位似变换。
一、单选题
1.如图所示,△OAB与△OCD是以点O为位似中心的位似图形,位似比为1:2,∠OCD=90°,CO=CD.若OB=1,则点C的坐标为(?? ) 21教育网
A.?(﹣1,2)??????????????????B.?( , )??????????????????C.?(﹣1,1)??????????????????D.?(1.﹣1)
2.如图,在平面直角坐标系中有两点A(6,2),B(6,0),以原点为位似中心,相似比为3∶1,把线段AB缩小得到A′B′,则过A′点对应点的反比例函数的解析式为(??? )www.21-cn-jy.com
A.?y= ??????????????????????????????B.?y= ??????????????????????????????C.?y=- ??????????????????????????????D.?y=
3.如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是(?? )【来源:21·世纪·教育·网】
A.?(4,2)???????????????????????????B.?(4,1)???????????????????????????C.?(5,2)???????????????????????????D.?(5,1)
4.在研究位似问题时,甲、乙同学的说法如下:
甲:如图①,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为(0,2).【来源:21cnj*y.co*m】
??
图①??????????????????????? 图②
乙:如图②,正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画△A1B1C1 , 使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,则点B1的坐标为(4,0).对于两人的观点,下列说法正确的是(???? )【出处:21教育名师】
A.?两人都对????????????????????????B.?两人都不对????????????????????????C.?甲对乙不对????????????????????????D.?甲不对乙对
二、填空题
5.如图,A是反比例函数y= ?(x>o)图象上一点,点B,D在y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3,△ABD的面积为1,则该反比例函数的表达式为________
6.如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为________. 21世纪教育网版权所有
7.如图,△AOB三个顶点的坐标分别为A(8,0),O(0,0),B(8,﹣6),点M为OB的中点.以点O为位似中心,把△AOB缩小为原来的 ,得到△A′O′B′,点M′为O′B′的中点,则MM′的长为________. 【版权所有:21教育】
8.如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为 ,点E的坐标为 ,则点P的坐标为________. 21cnjy.com
9.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是________.21*cnjy*com
10.如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1 , 其边长OA1缩小为OA的 ,经第二次变化后得正方形OA2B2C2 , 其边长OA2缩小为OA1的 ,经第三次变化后得正方形OA3B3C3 , 其边长OA3缩小为OA2的 ,…,依次规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=________.
三、综合题
11.在平面直角坐标系 中,已知 和 的顶点坐标分别为 、 、 、 、 、 .
按下列要求画图:以点 为位似中心,将 向 轴左侧按比例尺 放大得 的位似图形 ,并解决下列问题:
(1)顶点 的坐标为________, 的坐标为________, 的坐标为________;
(2)请你利用旋转、平移两种变换,使 通过变换后得到 ,且 ?恰与 拼接成一个平行四边形 (非正方形).写出符合要求的变换过程.
12.如图,△ABC三个顶点的坐标分别为A(-1,3),B(-1,1),C(-3,2).
请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2 , 求出△A1B1C1与△A2B2C2的面积.
13.请阅读下列材料,并完成相应的任务:
在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办法.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y,使得AX=BY=XY.(如图)解决这个问题的操作步骤如下:
第一步,在CA上作出一点D,使得CD=CB,连接BD.第二步,在CB上取一点Y',作Y'Z'∥CA,交BD于点Z',并在AB上取一点A',使Z'A'=Y'Z'.第三步,过点A作AZ∥A'Z',交BD于点Z.第四步,过点Z作ZY∥AC,交BC于点Y,再过点Y作YX∥ZA,交AC于点X.
则有AX=BY=XY.
下面是该结论的部分证明:
证明:∵AZ∥A'Z',∴∠BA'Z'=∠BAZ,
又∵∠A'BZ'=∠ABZ.∴△BA'Z'~△BAZ.
∴ ?.
同理可得 .∴ .
∵Z'A'=Y'Z',∴ZA=YZ.
任务:
(1)请根据上面的操作步骤及部分证明过程,判断四边形AXYZ的形状,并加以证明;
(2)请再仔细阅读上面的操作步骤,在(1)的基础上完成AX=BY=XY的证明过程;?
(3)上述解决问题的过程中,通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY,从而确定了点Z,Y的位置,这里运用了下面一种图形的变化是?? ?????? .
A.?平移????????????????????????????????????B.?旋转????????????????????????????????????C.?轴对称????????????????????????????????????D.?位似
答案解析部分
一、单选题
1.【答案】 C
解析:解:连接BC,
∵△OAB∽△OCD,相似比为1:2,
∴ ,
∵OB=1,
∴OD=2,
∴BD=OB,
∵CD=CO,
∴CB⊥OD,
∴BC=DB=OB=1,
∴C(-1,1),
故答案为:C.
连接BC,由位似比为1:2 可得OB与OD的比为 1:2 ,由OB=1,可得OD=2,由等腰三角形的三线合一可得BC=DB=OB=1,即可得出点C的坐标。
2.【答案】 B
解析:解:∵△A1B1O和△ABO以原点为位似中心,
∴△A1B1O∽△ABO,相似比为3:1,
∴A1B1= ,OB1=2,
∴A1的坐标为(2, )或(﹣2,﹣ ),
设过此点的反比例函数解析式为y= ,则k= ,
所以解析式为y= .
故答案为:B.
A点关于点O的位似点有两种情况,一种是在第一象限,一种是在第三象限,设出过点A1的反比例函数的解析式,将点坐标代入,得出k的值,最后得出相应的反比例函数解析式。
3.【答案】 C
解析:分别过C,D,A,B,做x轴的垂线,垂足分别是F,H,K;因为A,D的横坐标相同,所以D在AH上,∵E(1,0),C(2,2),A(3,4),D(3,1),∴EF=1,FH=1;∵CF∥AH∥BK,∴ ,∵CD∥AB,∴ ,∵DH∥BK,∴ ,∵EH=2,DH=1,∴EK=4,BK=2,∴OK=5,∴B(5,2),故答案为:C.2·1·c·n·j·y
分别过C,D,A,B,做x轴的垂线,垂足分别是F,H,K;根据位似图形对应线段的比等于相似比即可求得对应线段的比值,根据位似图形对应边互相平行或在同一直线上可得CD∥AB;再根据平行线分线段成比例定理可求解。
4.【答案】 A
解析:解:∵矩形ABCD和矩形EFGO 是位似图形,∴B和F是对应点,设直线BF为y=kx+b,则 ,解得: ?,∴ .∵位似中心是直线BF和CG的交点,∴x=0,∴y=2,∴位似中心为P(0,2),故甲正确;
由图可知,点B的坐标为(3,﹣2),以点C为位似中心,在网格中画△A1B1C1 , 使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,则点B1的坐标为(5,0),故乙正确.
故答案为:A.
位似图形是指对应顶点的连线相交于一点的两个相似多边形。甲:根据定义易知B和F是对应点,用待定系数法可求得BF的解析式,直线BF与y轴的交点的坐标即为位似中心P的坐标;乙:根据位似图形的定义和已知条件可知,即为直线CB与x轴的交点,用待定系数法可求得直线CB的坐标,再求出直线CB与x轴的交点坐标即可。
二、填空题
5.【答案】
解析:解:过A作AE⊥x轴 ∵△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似是1:3, ∴ ∴OE=AB, ∴ ∵OD∥AE ∴△COD∽△CEA ∴ 设BD=x,AB=y ∴DO=3x,AE=4x,CO=3y, ∵△ABD的面积为1, ∴xy=1, ∴xy=2, ∴AB?AE=4xy=8, 该反比例函数的表达式为:y= 故答案为:y=y=
过A作AE⊥x轴,根据位似的性质及OE=AB,可证得, 再证明△COD∽△CEA,得出对应成比例,就可证得, 设BD=x,AB=y,分别表示出DO、AE、CO,然后根据 △ABD的面积为1 ,求出xy的值,从而可求出AB?AE的值,根据反比例函数的几何意义,就可得到函数解析式。
6.【答案】 (-2,0)
解析:解:∵四边形OABC是矩形,点B的坐标为(2,4),
∴OC=AB=4,OA=2,
∴点C的坐标为:(0,4),
∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点E的坐标为(-1,2),
∴位似比为1:2,
∴OP:AP=OD:AB=1:2,
设OP=x,则 ,
解得:x=2,
∴OP=2,
即点P的坐标为:(-2,0).
故答案为:(-2,0)
位似图形对应点连线相交于位似中心,可确定位似比为1:2,再根据OP:AP=OD:AB即可求得OP长,即可写出P点坐标。
7.【答案】或
解析:解:如图,在Rt△AOB中,OB= =10, ∴OM=5,OM′= , ①当△A′OB′在第三象限时,MM′=5- = ; ②当△A″OB″在第二象限时,MM′=5+ = , 故答案为: 或 . 以O点为位似中心,作三个对应点的坐标,存在于第二象限和第四象限,根据存在的两种情况,可得出MM′的长度。
8.【答案】(-2,0)
解析:解:∵四边形OABC是矩形,点B的坐标为(2,4), ∴OC=AB=4,OA=2, ∴点C的坐标为:(0,4), ∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点E的坐标为(-1,2), ∴位似比为:2, ∴OP:AP=OD:AB=1:2, 设OP=x,则 ,解得:x=2, ∴OP=2, 即点P的坐标为:(-2,0) 故答案为:(-2,0) 由B点坐标,可求C点坐标,继而求出两个矩形的位似比,可简单利用三角形相似、对应边成比例来求得点P的坐标。
9.【答案】(2,2 )
解析:解:分别过A作AE⊥OB,CF⊥OB, ∵∠OCD=90°,∠AOB=60°, ∴∠ABO=∠CDO=30°,∠OCF=30°, ∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,点B的坐标是(6,0), ∴D(8,0),则DO=8, 故OC=4, 则FO=2,CF=CO?cos30°=4× =2 , 故点C的坐标是:(2,2 ). 故答案为:(2,2 ). 分别过A作AE⊥OB,CF⊥OB,利用∠OCD=90°,∠AOB=60°,可求出∠ABO=∠CDO=30°,∠OCF=30°,再根据已知:△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,点B的坐标是(6,0),求出DO、OC、OF的长,然后利用解直角三角形求出CF的长,就可得出点C的坐标。
10.【答案】16
解析:由已知有:OA1= OA;OA2= OA1= OA,OA3= OA2= OA,......,∴OAn= OA, OAn= OA= ,∴ = ,∴n=16.故答案为:16. 由题意和图形可得OAn=OA=,将OA的值代入计算即可求解。
三、综合题
11.【答案】(1)(﹣2,0);(﹣6,0);(﹣4,﹣2) (2)解:如图,把△A1B1C1绕点O顺时针旋转90°,再向右平移6个单位,向下平移1个单位,使B2C2与DE重合,或者:把△A1B1C1绕点O顺时针旋转90°,再向右平移6个单位,向上平移3个单位,使A2C2与EF重合,都可以拼成一个平行四边形.
解析:解:(1)如图所示,△A1B1C1即为所求作的三角形,A1(﹣2,0)B1(﹣6,0)C1(﹣4,﹣2);
(1)延长AO到A1 , 使A1O=2AO,延长BO到B1,使B1O=2BO,连接CO并延长到C1 , 使C1O=2CO,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标即可。 (2)先绕点O顺时针旋转90°,然后向右平移再向下(或向上)平移,使△A2B2C2的直角边与△DEF的直角边重合即可。
12.【答案】(1)解:如图所示,△A1B1C1即为所求,
(2)解:由题图得S△A1B1C1= ×2×2=2.∵将△A1B1C1放大为原来的2倍,得到△A2B2C2 , ∴△A1B1C1∽△A2B2C2 , ∴ = ,∴ = = ,
∴S△A2B2C2=4S△A1B1C1=4×2=8.
即S△A1B1C1=2,S△A2B2C2=8.
解析:【分析】(1)根据关于y轴对称的点横坐标互为相反数,纵坐标不变求出A,B,C三点的对称点A1,B1,C1三点的坐标,利用方格纸的特点描出A1,B1,C1三点,再顺次连接即可; (2)连接A1O并延长,在其延长线上取点A2 , 使OA2=2OA1 , 同理作出B2,C2,再顺次连接即可得到△A2B2C2,首先算出△A1B1C1的面积,由位似的性质知△A1B1C1∽△A2B2C2,根据相似三角形面积的比等于相似比的平方即可得出△A2B2C2的面积。
13.【答案】(1)解:四边形AXYZ是菱形.
证明:∵ZY∥AC,YX∥ZA,
∴四边形AXYZ是平行四边形.
∵ZA=YZ,
∴平行四边形AXYZ是菱形 (2)证明:∵CD=CB,
∴∠1=∠3.
∵ZY∥AC,
∴∠1=∠2.
∴∠2=∠3.
∴YB=YZ.
∵四边形AXYZ是菱形,
∴AX=XY=YZ.
∴AX=BY=XY (3)D
解析:解:(3)通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY,从而确定了点Z,Y的位置,此时四边形BA'Z'Y'∽四边形BAZY,所以该变换形式是位似变换.故答案是:D(或位似).
(1)四边形AXYZ是菱形.理由如下:根据两组对边分别平行的四边形是平行四边形,由ZY∥AC,YX∥ZA,得出四边形AXYZ是平行四边形,根据有一组邻边相等的平行四边形是菱形,由四边形AXYZ是平行四边形及ZA=YZ,得出结论:平行四边形AXYZ是菱形; (2)根据等边对等角,由CD=CB,得出∠1=∠3,由二直线平行同位角相等得出∠1=∠2,故∠2=∠3,根据等角对等边得出YB=YZ,根据菱形的性质得出∴AX=XY=YZ,从而得出结论; (3)通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY,从而确定了点Z,Y的位置,运用的位似变换。
同课章节目录
