浙教版八年级数学上册第1章 三角形的初步知识之全等三角形专题训练(无答案)
文档属性
| 名称 | 浙教版八年级数学上册第1章 三角形的初步知识之全等三角形专题训练(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 240.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-02 07:18:44 | ||
图片预览

文档简介
全等三角形专题训练
类型一(SAS)
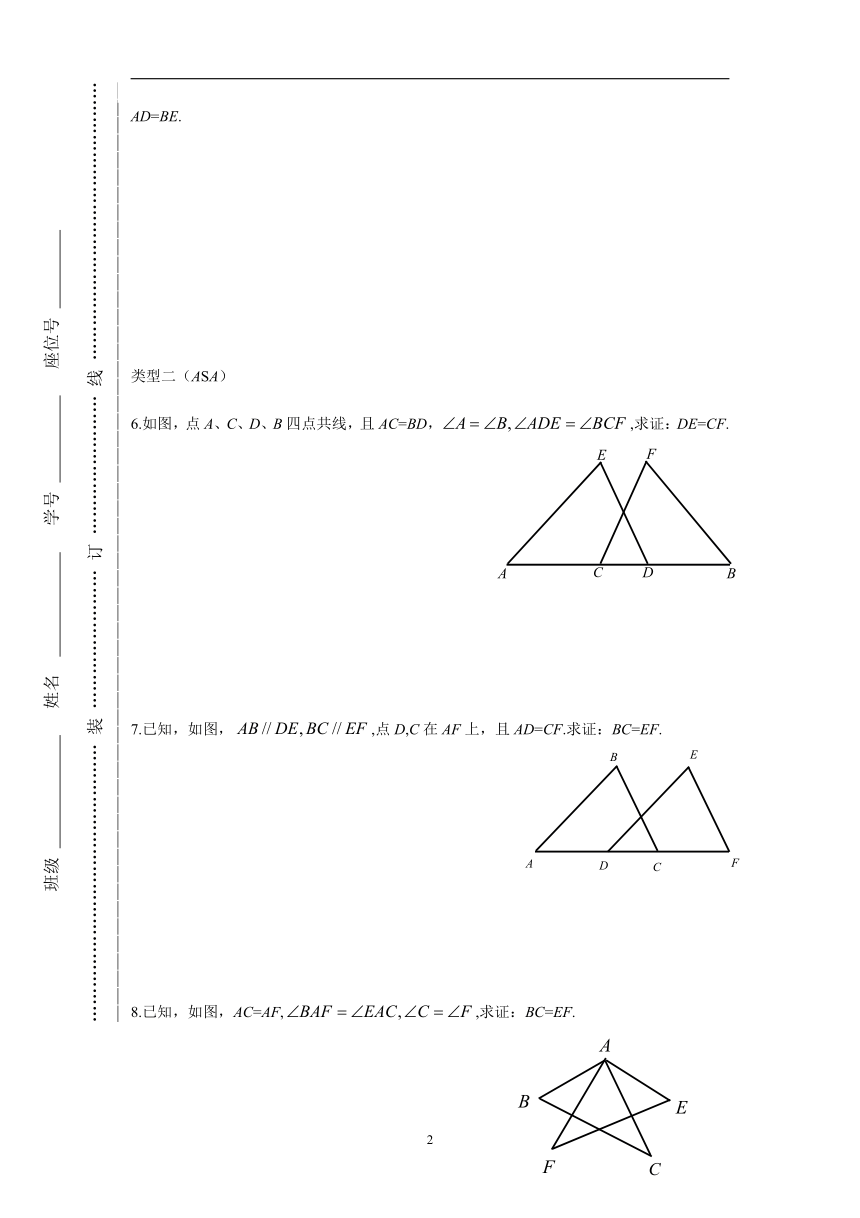
1. 已知,在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠E=∠C.
2.如图,已知,求证:.
3.如图,已知C为AB的中点,CD=CE,?∠1=∠2.求证:∠E=∠D.
4.如图,已知
5.如图,已知AC=BC,CD=CE,,且B,C,D在同一条直线上.求证:AD=BE.
类型二(ASA)
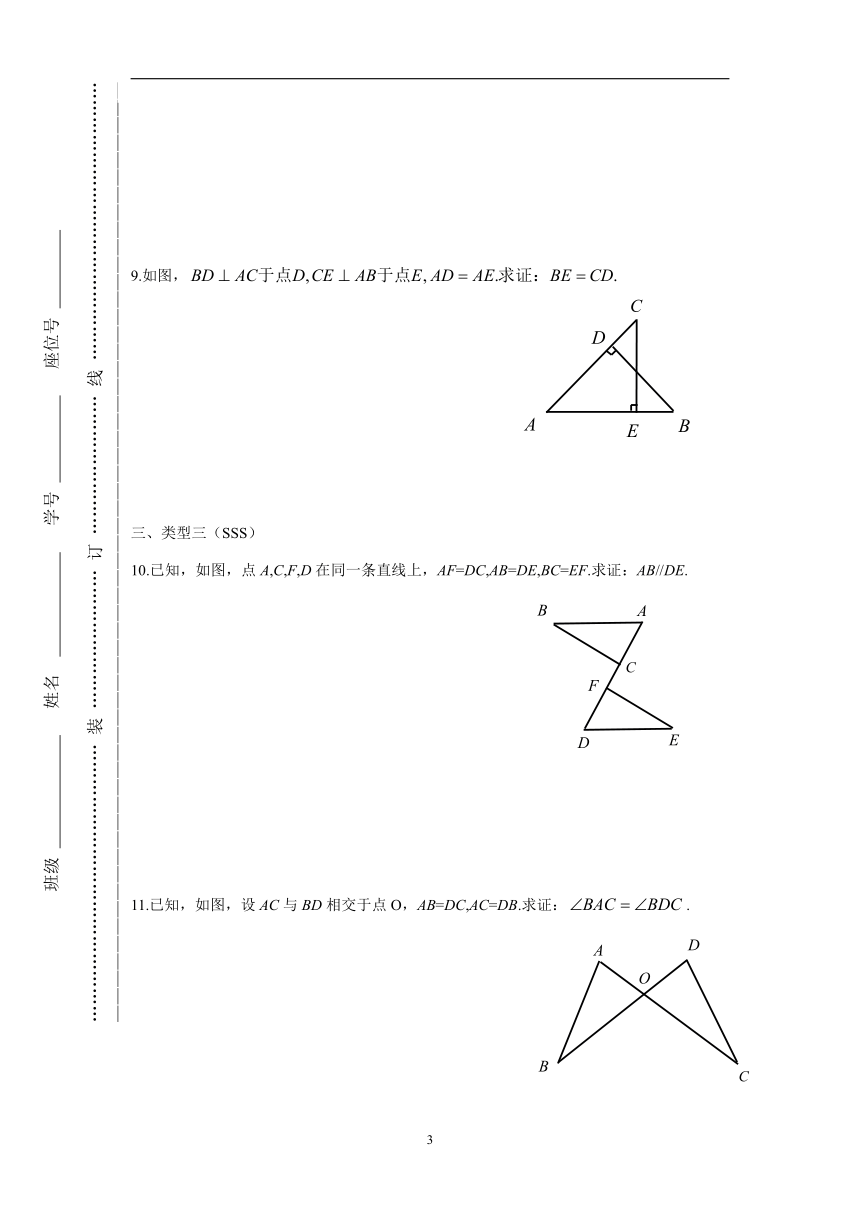
6.如图,点A、C、D、B四点共线,且AC=BD,,求证:DE=CF.
7.已知,如图,,点D,C在AF上,且AD=CF.求证:BC=EF.
8.已知,如图,AC=AF,,求证:BC=EF.
9.如图,
三、类型三(SSS)
10.已知,如图,点A,C,F,D在同一条直线上,AF=DC,AB=DE,BC=EF.求证:AB//DE.
11.已知,如图,设AC与BD相交于点O,AB=DC,AC=DB.求证:.
12.已知,如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:.
四、类型四(AAS)
13.如图,已知
14.如图所示,B,E,F,C四点在同一条直线上,,求证:OA=OD.
15.如图所示,
五、类型五(HL)
16.如图所示,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE.求证:AB//CD.
17.如图,已知∠C=∠D=90°,BC与AD交于点E,AC=BD,求证:AE=BE.
18.如图所示,已知AB=AE,BC=ED,,垂足为F,求证:CF=DF.
六、综合应用
19.(山东中考)如图,在△ABC中,AB=CB,,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.(1)求证:△ABE≌△CBD;(2)若,求的度数.
20.如图,已知CE,CB分别是△ABC与△ADC的中线,且.求证:CD=2CE.
21.如图,已知AC//BD,AE,BE分别平分和,CD过点E,求证:AB=AC+BD.
22.如图,中,AB=AC,E是AB上一点,F是AC延长线上一点,且BE=CF,若EF与BC相交于点D,求证:DE=DF.
23.如图所示,在四边形ABCD中,AC平分,AB>AD,DC=BC.求证.
类型一(SAS)
1. 已知,在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠E=∠C.
2.如图,已知,求证:.
3.如图,已知C为AB的中点,CD=CE,?∠1=∠2.求证:∠E=∠D.
4.如图,已知
5.如图,已知AC=BC,CD=CE,,且B,C,D在同一条直线上.求证:AD=BE.
类型二(ASA)
6.如图,点A、C、D、B四点共线,且AC=BD,,求证:DE=CF.
7.已知,如图,,点D,C在AF上,且AD=CF.求证:BC=EF.
8.已知,如图,AC=AF,,求证:BC=EF.
9.如图,
三、类型三(SSS)
10.已知,如图,点A,C,F,D在同一条直线上,AF=DC,AB=DE,BC=EF.求证:AB//DE.
11.已知,如图,设AC与BD相交于点O,AB=DC,AC=DB.求证:.
12.已知,如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:.
四、类型四(AAS)
13.如图,已知
14.如图所示,B,E,F,C四点在同一条直线上,,求证:OA=OD.
15.如图所示,
五、类型五(HL)
16.如图所示,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE.求证:AB//CD.
17.如图,已知∠C=∠D=90°,BC与AD交于点E,AC=BD,求证:AE=BE.
18.如图所示,已知AB=AE,BC=ED,,垂足为F,求证:CF=DF.
六、综合应用
19.(山东中考)如图,在△ABC中,AB=CB,,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.(1)求证:△ABE≌△CBD;(2)若,求的度数.
20.如图,已知CE,CB分别是△ABC与△ADC的中线,且.求证:CD=2CE.
21.如图,已知AC//BD,AE,BE分别平分和,CD过点E,求证:AB=AC+BD.
22.如图,中,AB=AC,E是AB上一点,F是AC延长线上一点,且BE=CF,若EF与BC相交于点D,求证:DE=DF.
23.如图所示,在四边形ABCD中,AC平分,AB>AD,DC=BC.求证.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
