第4章 相似三角形单元测试题（含答案）

中小学教育资源及组卷应用平台


衢州市教学联盟九年级数学第4章《相似三角形》
综合测试题（含答案）
[时间：120分钟 满分：120分]
一、选择题(每小题3分，共30分)
1.若两个相似多边形的面积之比为1：4，则它们的周长之比为（　）
A. 1：4? ????　　　　　???B. 1：2???????　　　　　 C. 2：1?????　　　　　??? D. 4：1
2. 我国国土面积约为960万平方千米，画在比例尺为1：1000万的地图上的面积约是（　）
A. 960平方千米??? B. 960平方米????? C. 960平方分米????? D. 960平方厘米
3. 如图，在△ABC中，DE∥BC，＝，BC＝12，则DE的长是(　 　)
A. 3 B. 4 C. 5 D. 6





4.如图，△ADE∽△ABC，?若AD=1，BD=2，则△ADE与△ABC的相似比是（??）
??A.?1：2??? B.?1：3??? C.?2：3??? D.?3：2
5.如图，在△ABC中，如果DE与BC不平行，那么下列条件中，不能判断△ADE∽△ACB的是(　　)
A.?∠ADE＝∠C??? B.?∠AED＝∠B???? C.??? ??D.?
6.如图，H为平行四边形ABCD中AD边上一点，且，AC和BH交于点K，则等于（????）
?1:2? ?????????????? ??B.?1:1??? ?????????? ??C.?1:3?? ???????? ?D.?2:3
7.如图，A,B,C,D在⊙O上，AC和BD相交于P点，若,且CD=3则AB的长为（　　）
A．9 B．6 C． D．



8. 如图，点A，B，C，D的坐标分别是(1，7)，(1，1)，(4，1)，(6，1)，以C，D，E为顶点的三角形与△ABC相似，则点E的坐标不可能是(　 　)
A. (6，0) B. (6，3) C. (6，5) D. (4，2)
9．如图，在平行四边形ABCD中，E是CD上的一点，DE： EC＝2 ：3，连接AE，BE，BD，且AE，BD交于点F，则S△DEF ：S△EBF ：S△ABF的值是(　　)
A. 2 ：5 ：25 B. 4 ：9 ：25 C. 2 ：3 ：5 D. 4 ：10 ：25
10.在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1交x轴于点A2，作正方形A2B2C2C1…按这样的规律进行下去，第2019个正方形的面积为?（???）
A．????? ?? B．?? ??C．????????? D．
二、填空题(每小题3分，共24分)
11. 已知线段a是线段b、c的比例中项，如果a=3，b=2，那么c=　　．
12. 已知点P是线段AB上的黄金分割点，PB＞PA，PB=2，那么PA=　　．
13.如图，O是△ABC的重心，延长CO，BO交对边于D，E，则S△DOE：S△BOC=________．
14. 如图，一个矩形的长边AF=a，短边AB=b，如果把这个矩形截去一个正方形后所余下的矩形与原矩形相似，那么=???????????????．




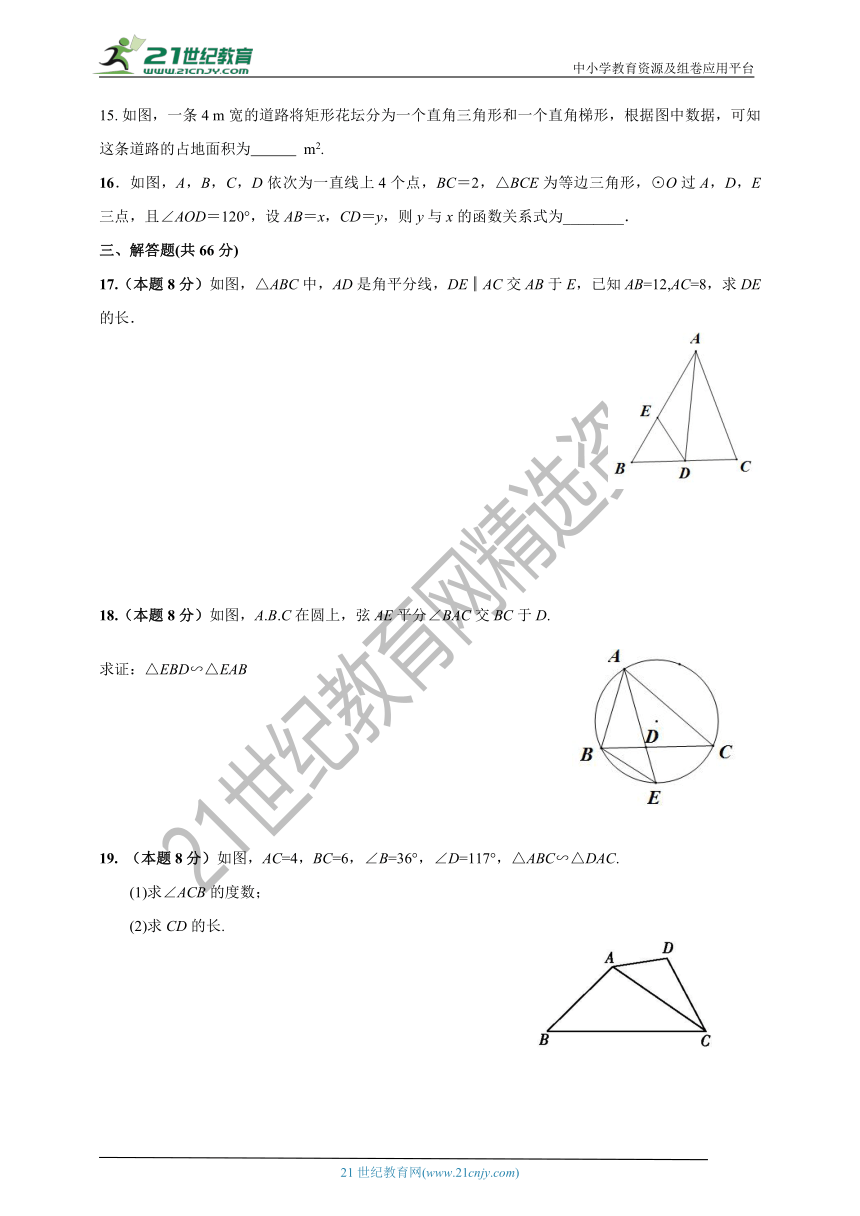
如图，一条4 m宽的道路将矩形花坛分为一个直角三角形和一个直角梯形，根据图中数据，可知这条道路的占地面积为　 　 m2.?
16．如图，A，B，C，D依次为一直线上4个点，BC＝2，△BCE为等边三角形，⊙O过A，D，E三点，且∠AOD＝120°，设AB＝x，CD＝y，则y与x的函数关系式为________．
解答题(共66分)
17.（本题8分）如图，△ABC中，AD是角平分线，DE║AC交AB于E，已知AB=12,AC=8，求DE的长．






18.（本题8分）如图，A.B.C在圆上，弦AE平分∠BAC交BC于D.
求证：△EBD∽△EAB




19. （本题8分）如图，AC=4，BC=6，∠B=36°，∠D=117°，△ABC∽△DAC.
(1)求∠ACB的度数；
(2)求CD的长.





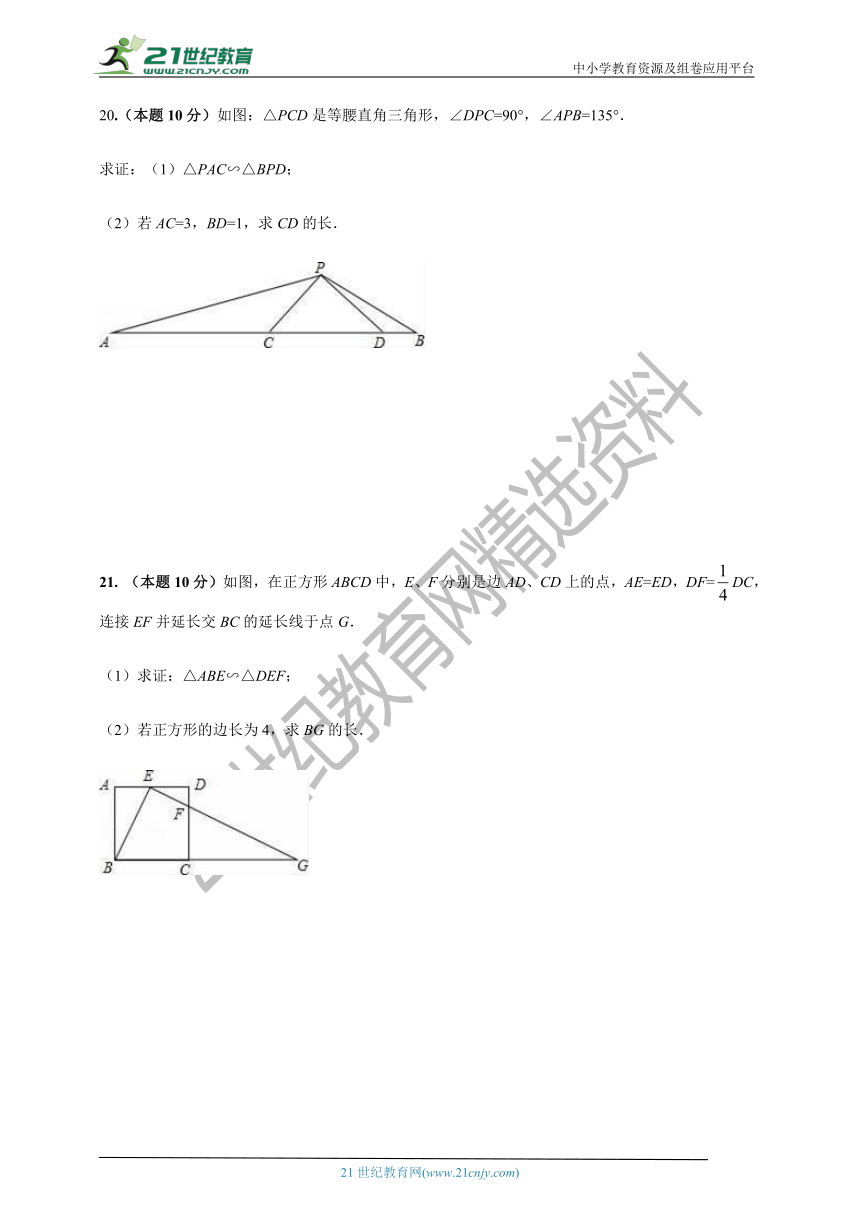
20.（本题10分）如图：△PCD是等腰直角三角形，∠DPC=90°，∠APB=135°．
求证：（1）△PAC∽△BPD；
（2）若AC=3，BD=1，求CD的长．






21. （本题10分）如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DF=DC，连接EF并延长交BC的延长线于点G．
（1）求证：△ABE∽△DEF；
（2）若正方形的边长为4，求BG的长．






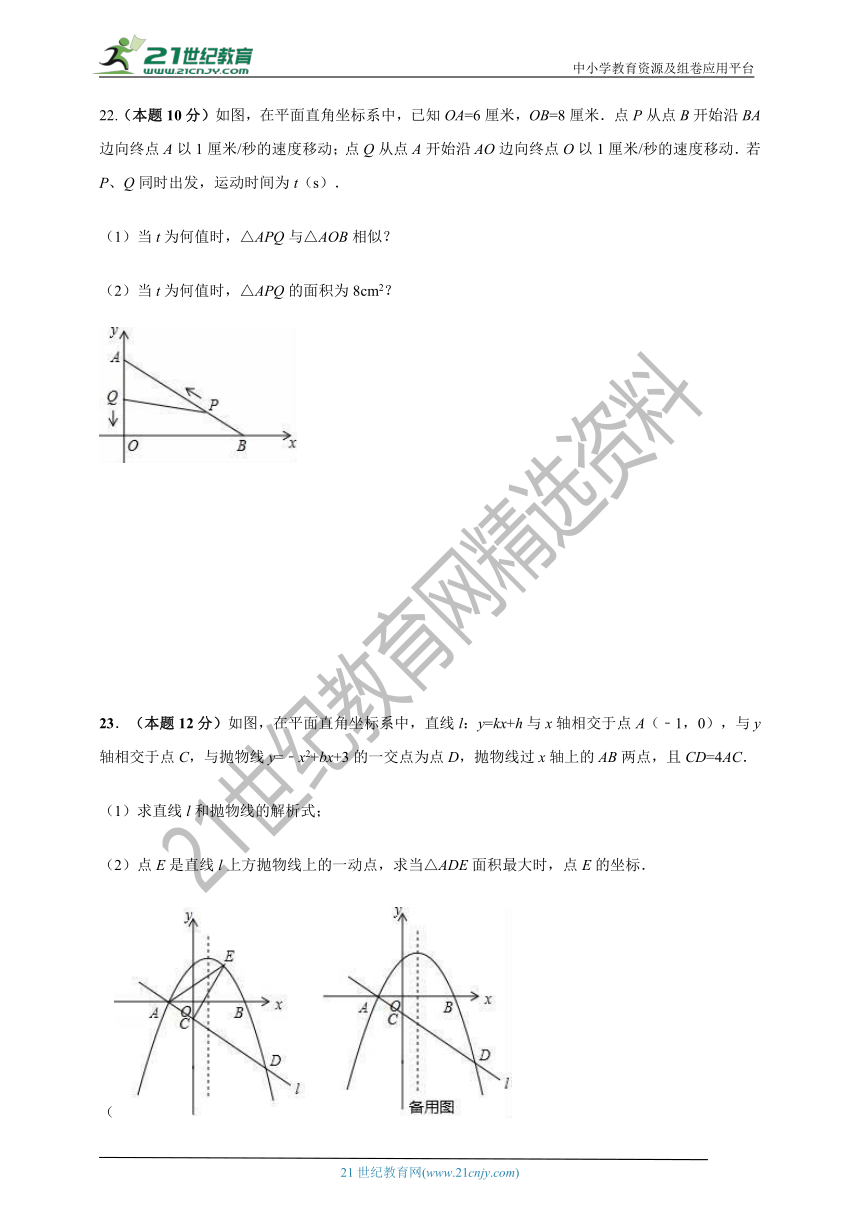
22.（本题10分）如图，在平面直角坐标系中，已知OA=6厘米，OB=8厘米．点P从点B开始沿BA边向终点A以1厘米/秒的速度移动；点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动．若P、Q同时出发，运动时间为t（s）．
（1）当t为何值时，△APQ与△AOB相似？
（2）当t为何值时，△APQ的面积为8cm2？







23．（本题12分）如图，在平面直角坐标系中，直线l：y=kx+h与x轴相交于点A（﹣1，0），与y轴相交于点C，与抛物线y=﹣x2+bx+3的一交点为点D，抛物线过x轴上的AB两点，且CD=4AC．
（1）求直线l和抛物线的解析式；
（2）点E是直线l上方抛物线上的一动点，求当△ADE面积最大时，点E的坐标．
（
答案：
选择题：BDBBC CABDD
填空题：


1：4

80

解答题：
DE=4.8.
18.∵AE平分∠BAC，∴∠EAB＝∠EAC，又∵∠EBC＝∠EAC，∴∠EBC＝∠EAB，又∵∠E公用，∴△EBD∽△EAB
19.解：(1)因为△ABC∽△DAC，∠D=117°，所以∠BAC=∠D=117°. 因为∠B=36°，所以∠ACB=180°－∠B－∠BAC=180°－36°－117°=27°.
(2)因为△ABC∽△DAC，AC=4，BC=6，所以=，即=，解得CD=.
20.（1）∵△PCD是等腰直角三角形，∠DPC=90°，∠APB=135°，∴∠APC+∠BPD=45°，
又∠PAB+∠PBA=45°，∠PBA+∠PBD=45°，∴∠PAB=∠PBD，∠BPD=∠PAC，
∵∠PCA=∠PDB，∴△PAC∽△BPD；
（2）∵PC=PD，AC=3，BD=1
∴PC=PD=，
∴CD==．
21.证明：∵ABCD为正方形，
∴AD=AB=DC=BC，∠A=∠D=90°，
∵AE=ED，
∴，
∵DF=DC，
∴，
∴，
∴△ABE∽△DEF；
（2）解：∵ABCD为正方形，
∴ED∥BG，
∴，
又∵DF=DC，正方形的边长为4，
∴ED=2，CG=6，
∴BG=BC+CG=10．
22.（1）∵点A（0，6），B（8，0），
∴AO=6，BO=8，
∴AB=10，
∵点P的速度是每秒1个单位，点Q的速度是每秒1个单位，
∴AQ=t，AP=10﹣t，
①∠APQ是直角时，△APQ∽△AOB，
，
解得t=6.25＞6，舍去；
②∠AQP是直角时，△AQP∽△AOB，
，
解得t=，
综上所述，t=秒时，△APQ与△AOB相似；
（2）如图，过点P作PC⊥OA于点C，

则PC=（10﹣t），
∴△APQ的面积=×t×（10﹣t）=8，
整理，得：t2﹣10t+20=0，
解得：t=5+＞6（舍去），或t=5﹣，
故当t=5﹣s时，△APQ的面积为8cm2．
23.（1）将A（﹣1，0）代入y=﹣x2+bx+3，得b=2，
所以抛物线的解析式为y=﹣x2+2x+3，
过点D作DF⊥x轴于点F，如图1

易证△AOC∽△AFD，
∴，
∵CD=4AC，
∴=，
∴点D横坐标为4，
把x=4代入y=﹣x2+2x+3，得y=﹣5，
∴D（4，﹣5），
把x=4，y=﹣5；x=﹣1，y=0代入y=kx+h，
解得，k=﹣1，h=﹣1，
∴直线l的解析式为y=﹣x﹣1．
（2）过点E作EM⊥x轴，交AD于点M，如图2

设点E（m，﹣m2+2m+3），则M（m，﹣m﹣1），
∴EM=﹣m2+2m+3﹣（﹣m﹣1）═﹣m2+3m+4，
∴S△ADE=，
当m=时，△ADE的面积最大，
此时，E．









第3题图 第4题图 第5题图 第6题图


第7题图 第8题图 第9题图 第10题图




第13题图 第14题图 第15题图 第16题图









21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)