6.5 角与角的度量-角的概念 同步训练(解析版)
文档属性
| 名称 | 6.5 角与角的度量-角的概念 同步训练(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-29 11:07:51 | ||
图片预览

文档简介
初中数学浙教版七年级上册6.5 角与角的度量-角的概念 同步训练
一、基础夯实
1.下列图形中能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( ??)
A.?????????????B.?????????????C.?????????????D.?
2.下列表示角的方法中,不正确的是(???? )
A.?∠A??????????????????????????????????????B.?∠ ??????????????????????????????????????C.?∠ ??????????????????????????????????????D.?∠
3.如图,下列说法:
①∠ECG和∠C是同一个角;②∠OGF和∠DGB是同一个角;③∠DOF和∠EOG是同一个角;④∠ABC和∠CBD是同一个角.21世纪教育网版权所有
其中正确的说法有 (??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.如图,∠1,∠2表示的角可分别用大写字母表示为________,________;∠A也可表示为________,还可以表示为________.21教育网
5.如图,图中可以只用一个大写字母表示的角有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
6.下列语句正确的是(??? )
A.?一条直线可以看成一个平角????????????????????????????????B.?周角是一条射线 C.?角是由一条射线旋转而成的????????????????????????????????D.?角是由公共端点的两条射线组成的图形
7.下列说法错误的是(??? )
A.?∠AOB的顶点是O????????????????????????????????????????????????B.?∠AOB的边是两条射线 C.?射线BO,射线AO分别是表示∠AOB的两边?????????D.?∠AOB与∠BOA表示同一个角
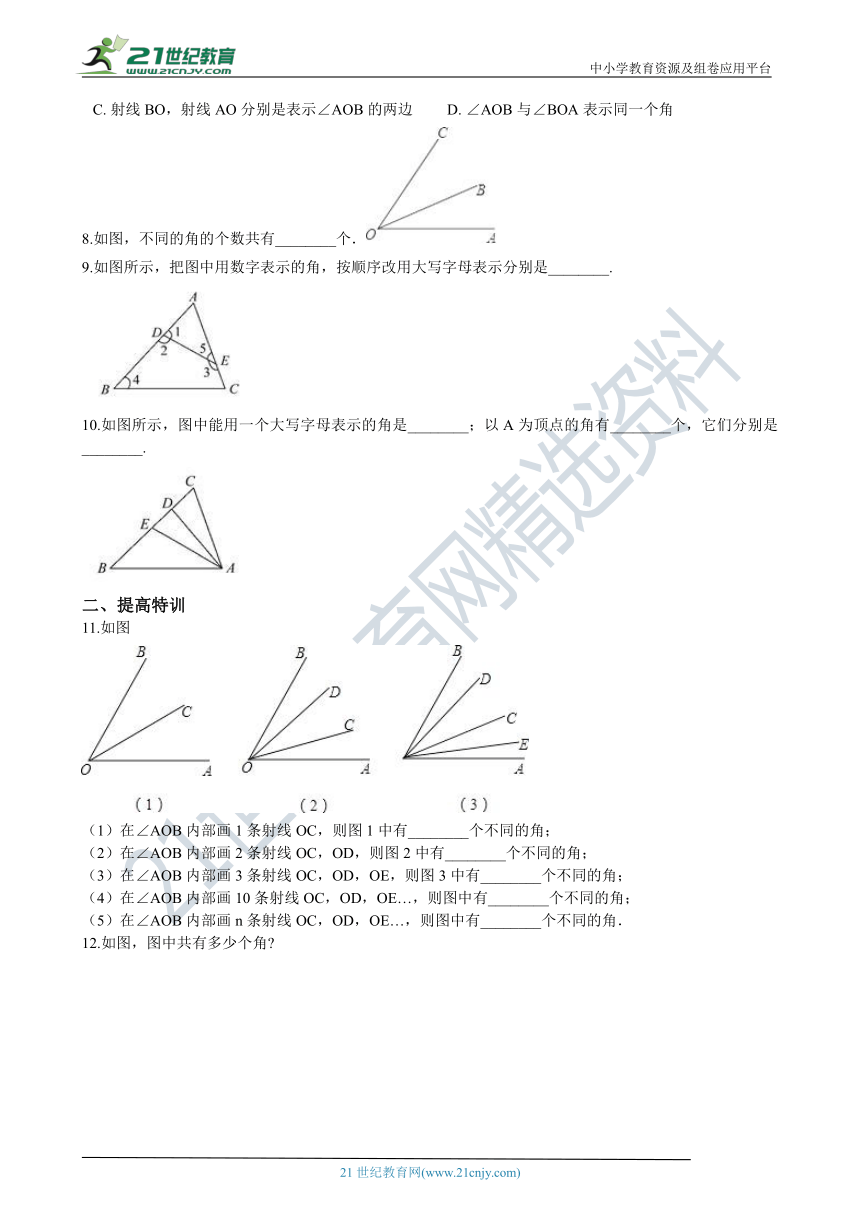
8.如图,不同的角的个数共有________个.
9.如图所示,把图中用数字表示的角,按顺序改用大写字母表示分别是________.
10.如图所示,图中能用一个大写字母表示的角是________;以A为顶点的角有________个,它们分别是________. 21·cn·jy·com
二、提高特训
11.如图
(1)在∠AOB内部画1条射线OC,则图1中有________个不同的角;
(2)在∠AOB内部画2条射线OC,OD,则图2中有________个不同的角;
(3)在∠AOB内部画3条射线OC,OD,OE,则图3中有________个不同的角;
(4)在∠AOB内部画10条射线OC,OD,OE…,则图中有________个不同的角;
(5)在∠AOB内部画n条射线OC,OD,OE…,则图中有________个不同的角.
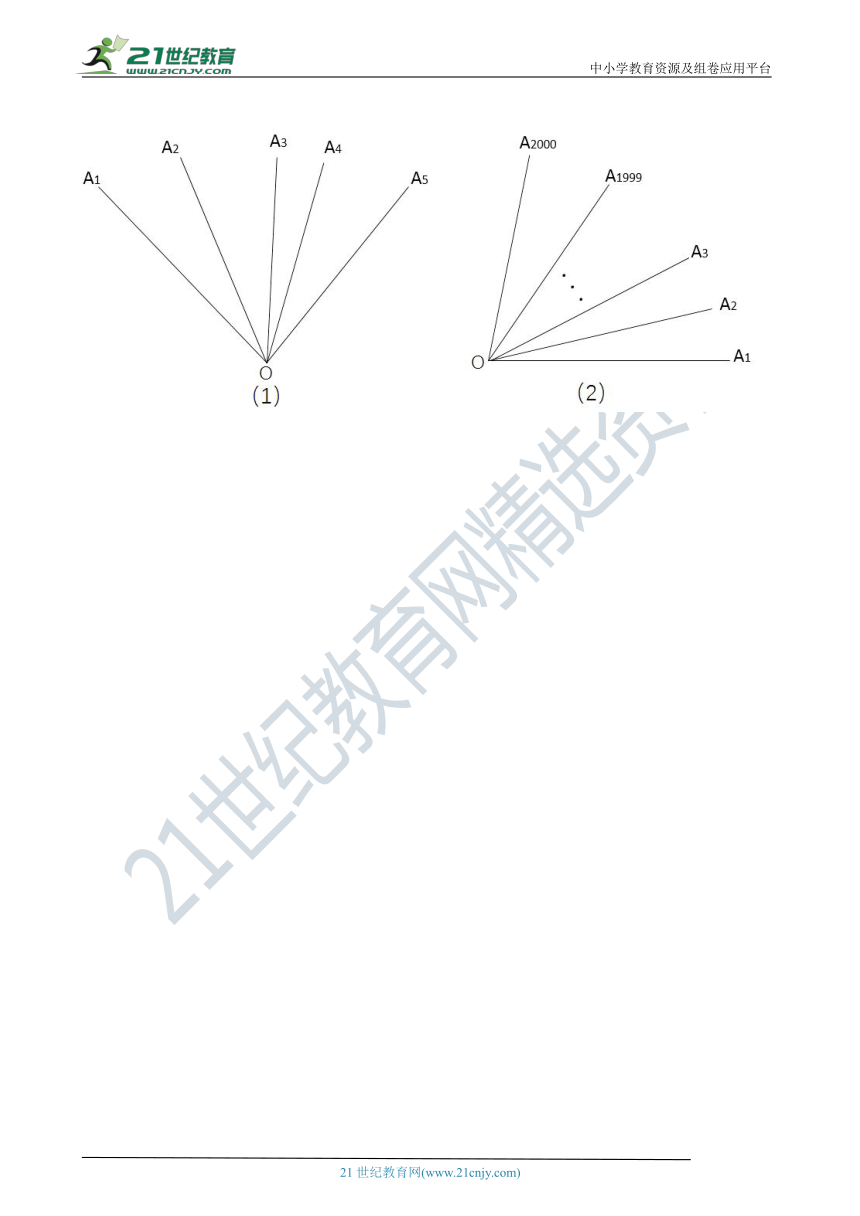
12.如图,图中共有多少个角?
答案解析部分
一、基础夯实
1. B
解:A、不能用∠1,∠AOB,∠O三种方法表示同一个角,故A不符合题意;
B、能用∠1,∠AOB,∠O三种方法表示同一个角,故B符合题意;
C、不能用∠1,∠AOB,∠O三种方法表示同一个角,故C不符合题意;
D、不能用∠1,∠AOB,∠O三种方法表示同一个角,故D不符合题意;
故答案为:B.
【分析】角可以用一个大写字母表示,也可以用三个大写字母表示,其中顶点字母要写在中间,当顶点处只有一个角时,才能用顶点处的一个字母表示,否则分不清这个字母表示的是哪个角;角还可以用一个希腊字母表示或阿拉伯数字表示,据此判断即可.www.21-cn-jy.com
2. B
解:图中的角有∠A、∠1、∠α、∠AEC,
即表示方法不正确的有∠E,
故答案为:B.
【分析】由图知,以点E为顶点的角不唯一,所以不能用∠E表示角,应用三个大写字母表示。
3. C
解: ①?根据角的表示方式,可知∠ECG和∠C是同一个角,说法正确; ②?同理∠OGF和∠DGB也是同一个角,说法正确;∠DOF和∠EOG是对顶角,但不是同一个角,说法错误; ④ ∠ABC和∠CBD是同一个角,说法正确。 故答案为:C。 【分析】根据角的表示方式以及角的概念,可以看出两个角是否为同一个角,进行判断即可。
4.∠ABC;∠BCN;∠BAC;∠MAN
解:∠1=∠ABC,∠2=∠BCN, ∠A=∠BAC或∠MAN
【分析】表示一个角共有4种方法,①以某个点为顶点的角只有一个的时候,可以用角的符号加表顶点的大写字母来表示,如∠A,②用角的两边上的任意一个大写字母和角的顶点的字母来表示,如∠BAC,其中A为角的顶点;③用数字加弧线书写在角的内部来表示,如∠1、∠2等;④用希腊字母加弧线书写在角的内部来表示,类似于用数字来表示一样,如∠α、∠β等,根据角的表示方法即可一一得出答案。
5.B
解:可以只用一个大写字母表示的角有∠A,∠C,故答案为:B
【分析】根据图形可知顶点A、C处只有一个角,可以只用一个大写字母表示.
6.D
解:具有公共端点的两条射线组成的图形叫做角,故答案为:D
【分析】根据角的定义具有公共端点的两条射线组成的图形,得到正确选项.
7. C
解:A、“∠AOB的顶点是点O”这种说法是正确的,不符合题意;
B、“∠AOB的边是两条射线”这种说法是正确的,不符合题意;
C、“射线BO,射线AO分别表示∠AOB的两边”这种说法是错误的,因为∠AOB的两边是射线OA和射线OB,符合题意;2·1·c·n·j·y
D、“∠AOB与∠BOA表示同一个角”这种说法是正确的,不符合题意;
故答案为:C.
【分析】有公共端点的两条射线所组成的图形就是角,角的两条边是两条射线;在用三个大写字母表示角的时候,表顶点的字母一定要写在中间,另两个字母在角的两条边上随便取一点,用表这个点的大写字母来表示即可,至于那条边上的字母写在前面没有要求。【来源:21·世纪·教育·网】
8.3
解:图中的角有∠AOB,∠BOC,∠AOC,共3个角,故答案为:3【分析】顶点O处共有3条射线,共有角3×(3-1)÷2个角.21·世纪*教育网
9. ∠ADE,∠BDE,∠DEC,∠ABC,∠AED
解:∠1=∠ADE,∠2=∠BDE,∠3=∠DEC,∠4=∠ABC,∠5=∠AED。 故答案为:∠ADE,∠BDE,∠DEC,∠ABC,∠AED。 【分析】找出数字表示的角的顶点,将其用大写字母进行表示即可。www-2-1-cnjy-com
10. ∠B,∠C;6;∠CAD,∠CAE,∠CAB,∠DAE,∠DAB,∠EAB
解:∠B和∠C不再包含其余的角,所以可用一个大写字母表示;以A为顶点的角有∠CAD,∠CAE,∠CAB,∠DAE,∠DAB,∠EAB共有6个。 故答案为:∠B,∠C;6;∠CAD,∠CAE,∠CAB,∠DAE,∠DAB,∠EAB。 【分析】能用一个大写字母表示的角,其角中不包含其余的角;以A为顶点的角,按照从小到大的原则进行计数即可。2-1-c-n-j-y
二、提高特训
11.(1)3(2)6(3)10(4)66(5)
解:⑴在∠AOB内部画1条射线OC,则图中有3个不同的角,故答案为:3.
⑵在∠AOB内部画2条射线OC,OD,则图中有6个不同的角,
故答案为:6.
⑶在∠AOB内部画3条射线OC,OD,OE,则图中有10个不同的角,
故答案为:10.
⑷在∠AOB内部画10条射线OC,OD,OE,…,则图中有1+2+3+…+10+11=66个不同的角,
故答案为:66.
⑸在∠AOB内部画n条射线OC,OD,OE,…,则图中有1+2+3+…+n+(n+1)= 个不同的角.
故答案为: .
【分析】(1)根据图形数出即可;(2)根据图形数出即可;(3)根据图形数出即可;(4)有1+2+3+…+9+10+11=66个角;(5)求出1+2+3+…+n+(n+1)的值即可.21cnjy.com
12. 解:图(1):从图中可以看出,最大的角∠A1OA5被三条射线OA2、OA3、OA4分成4个部分,从左往右,先数以OA1为左边的角,有∠A1OA2 , ∠A1OA3 , ∠A1OA4 , ∠A1OA5 , 共4个;再数以OA2为左边的角,有∠A2OA3 , ∠A2OA4 , ∠A2OA5 , 共3个;依此类推,以OA3 , OA4为左边的角,分别有2,1个, ∴图(1)中角的个数为:4+3+2+1=10(个); 图(2):从图中可以看出,最大的角∠A1OA2000被1998条射线OA2、OA3、OA4……OA1999分成1999个部分,从左往右,先数以OA1为左边的角,有∠A1OA2 , ∠A1OA3 , ∠A1OA4 , ∠A1OA5 , ……,∠A1OA2000 , 共1999个;再数以OA2为左边的角,有∠A2OA3 , ∠A2OA4 , ∠A2OA5 , ……,∠A2OA2000 , 共1998个;依此类推,以OA3 , OA4 , ……OA1999为左边的角,分别有1997,1996,……1个, ∴图(2)中角的个数为:1999+1998+……+1=""=1999000(个).
【分析】数图中角的个数和数线段一样,要不重不漏,因此,必须按照一定的规律去数.
一、基础夯实
1.下列图形中能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( ??)
A.?????????????B.?????????????C.?????????????D.?
2.下列表示角的方法中,不正确的是(???? )
A.?∠A??????????????????????????????????????B.?∠ ??????????????????????????????????????C.?∠ ??????????????????????????????????????D.?∠
3.如图,下列说法:
①∠ECG和∠C是同一个角;②∠OGF和∠DGB是同一个角;③∠DOF和∠EOG是同一个角;④∠ABC和∠CBD是同一个角.21世纪教育网版权所有
其中正确的说法有 (??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.如图,∠1,∠2表示的角可分别用大写字母表示为________,________;∠A也可表示为________,还可以表示为________.21教育网
5.如图,图中可以只用一个大写字母表示的角有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
6.下列语句正确的是(??? )
A.?一条直线可以看成一个平角????????????????????????????????B.?周角是一条射线 C.?角是由一条射线旋转而成的????????????????????????????????D.?角是由公共端点的两条射线组成的图形
7.下列说法错误的是(??? )
A.?∠AOB的顶点是O????????????????????????????????????????????????B.?∠AOB的边是两条射线 C.?射线BO,射线AO分别是表示∠AOB的两边?????????D.?∠AOB与∠BOA表示同一个角
8.如图,不同的角的个数共有________个.
9.如图所示,把图中用数字表示的角,按顺序改用大写字母表示分别是________.
10.如图所示,图中能用一个大写字母表示的角是________;以A为顶点的角有________个,它们分别是________. 21·cn·jy·com
二、提高特训
11.如图
(1)在∠AOB内部画1条射线OC,则图1中有________个不同的角;
(2)在∠AOB内部画2条射线OC,OD,则图2中有________个不同的角;
(3)在∠AOB内部画3条射线OC,OD,OE,则图3中有________个不同的角;
(4)在∠AOB内部画10条射线OC,OD,OE…,则图中有________个不同的角;
(5)在∠AOB内部画n条射线OC,OD,OE…,则图中有________个不同的角.
12.如图,图中共有多少个角?
答案解析部分
一、基础夯实
1. B
解:A、不能用∠1,∠AOB,∠O三种方法表示同一个角,故A不符合题意;
B、能用∠1,∠AOB,∠O三种方法表示同一个角,故B符合题意;
C、不能用∠1,∠AOB,∠O三种方法表示同一个角,故C不符合题意;
D、不能用∠1,∠AOB,∠O三种方法表示同一个角,故D不符合题意;
故答案为:B.
【分析】角可以用一个大写字母表示,也可以用三个大写字母表示,其中顶点字母要写在中间,当顶点处只有一个角时,才能用顶点处的一个字母表示,否则分不清这个字母表示的是哪个角;角还可以用一个希腊字母表示或阿拉伯数字表示,据此判断即可.www.21-cn-jy.com
2. B
解:图中的角有∠A、∠1、∠α、∠AEC,
即表示方法不正确的有∠E,
故答案为:B.
【分析】由图知,以点E为顶点的角不唯一,所以不能用∠E表示角,应用三个大写字母表示。
3. C
解: ①?根据角的表示方式,可知∠ECG和∠C是同一个角,说法正确; ②?同理∠OGF和∠DGB也是同一个角,说法正确;∠DOF和∠EOG是对顶角,但不是同一个角,说法错误; ④ ∠ABC和∠CBD是同一个角,说法正确。 故答案为:C。 【分析】根据角的表示方式以及角的概念,可以看出两个角是否为同一个角,进行判断即可。
4.∠ABC;∠BCN;∠BAC;∠MAN
解:∠1=∠ABC,∠2=∠BCN, ∠A=∠BAC或∠MAN
【分析】表示一个角共有4种方法,①以某个点为顶点的角只有一个的时候,可以用角的符号加表顶点的大写字母来表示,如∠A,②用角的两边上的任意一个大写字母和角的顶点的字母来表示,如∠BAC,其中A为角的顶点;③用数字加弧线书写在角的内部来表示,如∠1、∠2等;④用希腊字母加弧线书写在角的内部来表示,类似于用数字来表示一样,如∠α、∠β等,根据角的表示方法即可一一得出答案。
5.B
解:可以只用一个大写字母表示的角有∠A,∠C,故答案为:B
【分析】根据图形可知顶点A、C处只有一个角,可以只用一个大写字母表示.
6.D
解:具有公共端点的两条射线组成的图形叫做角,故答案为:D
【分析】根据角的定义具有公共端点的两条射线组成的图形,得到正确选项.
7. C
解:A、“∠AOB的顶点是点O”这种说法是正确的,不符合题意;
B、“∠AOB的边是两条射线”这种说法是正确的,不符合题意;
C、“射线BO,射线AO分别表示∠AOB的两边”这种说法是错误的,因为∠AOB的两边是射线OA和射线OB,符合题意;2·1·c·n·j·y
D、“∠AOB与∠BOA表示同一个角”这种说法是正确的,不符合题意;
故答案为:C.
【分析】有公共端点的两条射线所组成的图形就是角,角的两条边是两条射线;在用三个大写字母表示角的时候,表顶点的字母一定要写在中间,另两个字母在角的两条边上随便取一点,用表这个点的大写字母来表示即可,至于那条边上的字母写在前面没有要求。【来源:21·世纪·教育·网】
8.3
解:图中的角有∠AOB,∠BOC,∠AOC,共3个角,故答案为:3【分析】顶点O处共有3条射线,共有角3×(3-1)÷2个角.21·世纪*教育网
9. ∠ADE,∠BDE,∠DEC,∠ABC,∠AED
解:∠1=∠ADE,∠2=∠BDE,∠3=∠DEC,∠4=∠ABC,∠5=∠AED。 故答案为:∠ADE,∠BDE,∠DEC,∠ABC,∠AED。 【分析】找出数字表示的角的顶点,将其用大写字母进行表示即可。www-2-1-cnjy-com
10. ∠B,∠C;6;∠CAD,∠CAE,∠CAB,∠DAE,∠DAB,∠EAB
解:∠B和∠C不再包含其余的角,所以可用一个大写字母表示;以A为顶点的角有∠CAD,∠CAE,∠CAB,∠DAE,∠DAB,∠EAB共有6个。 故答案为:∠B,∠C;6;∠CAD,∠CAE,∠CAB,∠DAE,∠DAB,∠EAB。 【分析】能用一个大写字母表示的角,其角中不包含其余的角;以A为顶点的角,按照从小到大的原则进行计数即可。2-1-c-n-j-y
二、提高特训
11.(1)3(2)6(3)10(4)66(5)
解:⑴在∠AOB内部画1条射线OC,则图中有3个不同的角,故答案为:3.
⑵在∠AOB内部画2条射线OC,OD,则图中有6个不同的角,
故答案为:6.
⑶在∠AOB内部画3条射线OC,OD,OE,则图中有10个不同的角,
故答案为:10.
⑷在∠AOB内部画10条射线OC,OD,OE,…,则图中有1+2+3+…+10+11=66个不同的角,
故答案为:66.
⑸在∠AOB内部画n条射线OC,OD,OE,…,则图中有1+2+3+…+n+(n+1)= 个不同的角.
故答案为: .
【分析】(1)根据图形数出即可;(2)根据图形数出即可;(3)根据图形数出即可;(4)有1+2+3+…+9+10+11=66个角;(5)求出1+2+3+…+n+(n+1)的值即可.21cnjy.com
12. 解:图(1):从图中可以看出,最大的角∠A1OA5被三条射线OA2、OA3、OA4分成4个部分,从左往右,先数以OA1为左边的角,有∠A1OA2 , ∠A1OA3 , ∠A1OA4 , ∠A1OA5 , 共4个;再数以OA2为左边的角,有∠A2OA3 , ∠A2OA4 , ∠A2OA5 , 共3个;依此类推,以OA3 , OA4为左边的角,分别有2,1个, ∴图(1)中角的个数为:4+3+2+1=10(个); 图(2):从图中可以看出,最大的角∠A1OA2000被1998条射线OA2、OA3、OA4……OA1999分成1999个部分,从左往右,先数以OA1为左边的角,有∠A1OA2 , ∠A1OA3 , ∠A1OA4 , ∠A1OA5 , ……,∠A1OA2000 , 共1999个;再数以OA2为左边的角,有∠A2OA3 , ∠A2OA4 , ∠A2OA5 , ……,∠A2OA2000 , 共1998个;依此类推,以OA3 , OA4 , ……OA1999为左边的角,分别有1997,1996,……1个, ∴图(2)中角的个数为:1999+1998+……+1=""=1999000(个).
【分析】数图中角的个数和数线段一样,要不重不漏,因此,必须按照一定的规律去数.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
