第4章 图形与坐标单元检测卷（含答案）

中小学教育资源及组卷应用平台


衢州市教学联盟浙教版八上数学图形与坐标检测卷
时间：90分钟　满分：100分　班级：　　　　　　　姓名：　　　　　　
选择题(每小题3分，共30分)
1．点P（4，﹣3）到x轴的距离是（ ）
A．4??? 　　　　　　　B．3??? 　　　　　　C．﹣3?　　　　　　　 D．5
2．根据下列表述，能确定位置的是（ 　　）
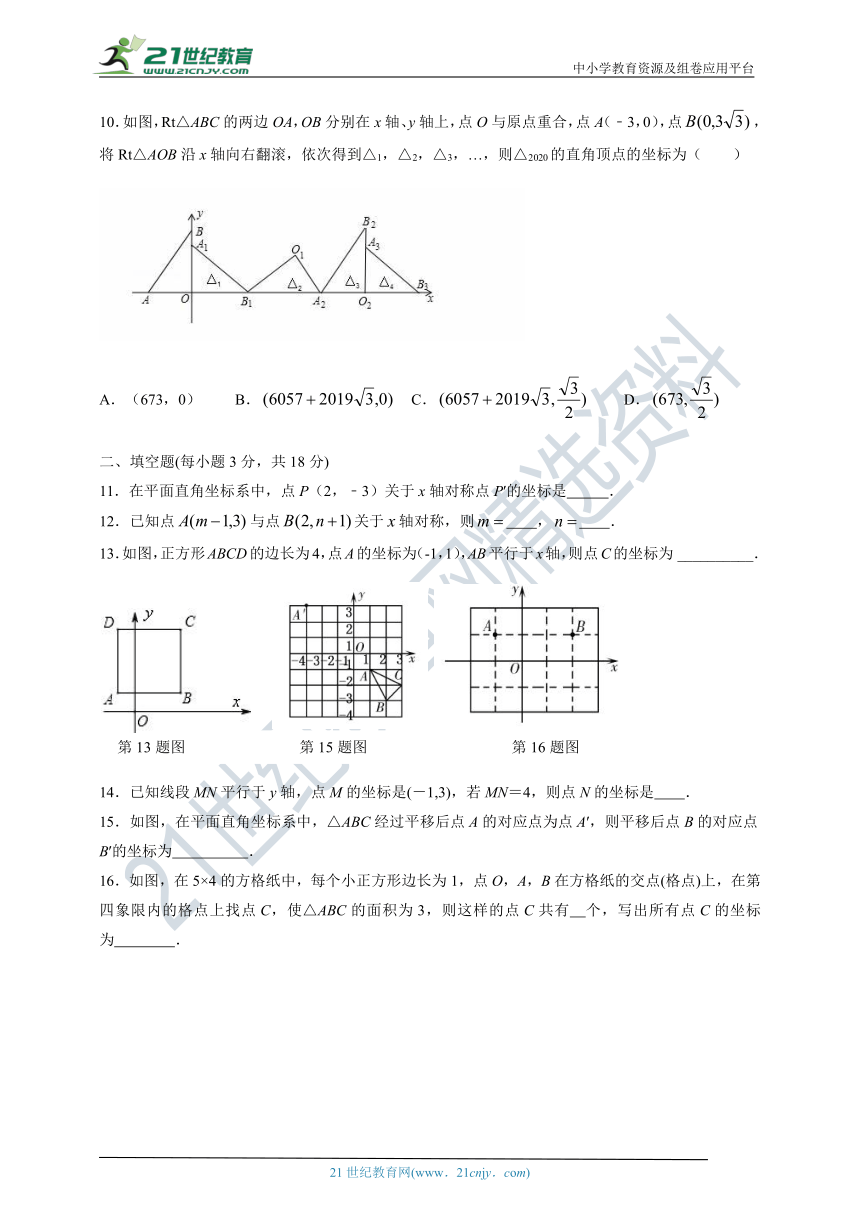
A．运城空港北区?????????????????????????????????????B．给正达广场3楼送东西?????
C．康杰初中偏东35°??????????????????????????????D．东经120°，北纬30°
3．如图，将长BC=3 的长方形ABCD放在平面直角坐标系中，
若AD∥x轴，且点D(6,3)，则A点的坐标为( )
A．(5,3) 　　　　　　 B．(4,3)　　　　　 C．(4,2) 　　　　　　　D．(3,3)
4．如果点在第四象限,则a的取值范围是（???）
??A．???????　　　　??B．????????　　　?C．?????　　　　　???D．
5．若点在轴上，则点P的坐标为（? ）
A．?????????　　　　 B．? ????????　　　　??C．????　　　???? D．??????
6．已知点P(a＋1,2a－3)关于x轴的对称点在第一象限，则a的取值范围是( )
A．a＜－1 　　 B．－1＜a＜ 　　 C．－＜a＜1 D．a＞
7．设三角形三个顶点的坐标分别为A(0,0)，B(3,0)，C(3，－3)，则这个三角形是( )
A．等边三角形 　　　B．任意三角形　　　　　 C．等腰直角三角形 D．钝角三角形
8．点不可能在（　）
A．第一象限????????　　　??B．第二象限???????????　　　??C．第三象限????　　????D．第四象限??
9．点P的坐标为(2－a,3a＋6)，且到两坐标轴的距离相等，则点P的坐标为( )
A．(3,3) 　　　　　　　B．(3，－3)　　　　　 C．或 D．(3,3)或(6，－6)
10．如图，Rt△ABC的两边OA，OB分别在x轴、y轴上，点O与原点重合，点A（﹣3，0），点，将Rt△AOB沿x轴向右翻滚，依次得到△1，△2，△3，…，则△2020的直角顶点的坐标为（　　）

（673，0）?????????B． C．?????????D．
二、填空题(每小题3分，共18分)
11．在平面直角坐标系中，点P（2，﹣3）关于x轴对称点P′的坐标是　???　．
12．已知点与点关于轴对称，则????????，????????．
13．如图，正方形ABCD的边长为4，点A的坐标为（-1，1），AB平行于x轴，则点C的坐标为?__________．








14．已知线段MN平行于y轴，点M的坐标是(－1,3)，若MN＝4，则点N的坐标是　　．
15．如图，在平面直角坐标系中，△ABC经过平移后点A的对应点为点A′，则平移后点B的对应点B′的坐标为　　　　　．
16．如图，在5×4的方格纸中，每个小正方形边长为1，点O，A，B在方格纸的交点(格点)上，在第四象限内的格点上找点C，使△ABC的面积为3，则这样的点C共有　个，写出所有点C的坐标为　 　．







三、解答题(共52分)
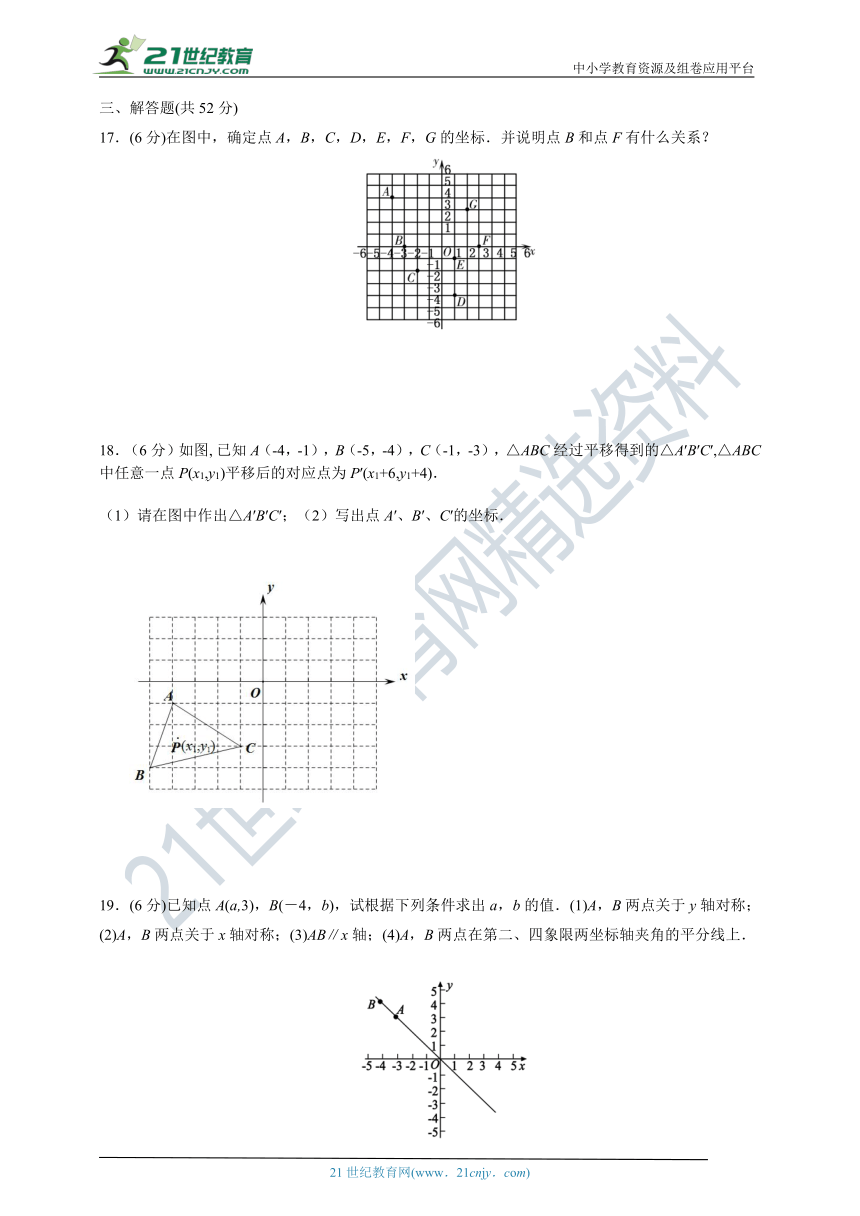
17．(6分)在图中，确定点A，B，C，D，E，F，G的坐标．并说明点B和点F有什么关系？




18．（6分）如图,?已知A（-4，-1），B（-5，-4），C（-1，-3），△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)．
（1）请在图中作出△A′B′C′；（2）写出点A′、B′、C′的坐标． ? ????





19．(6分)已知点A(a,3)，B(－4，b)，试根据下列条件求出a，b的值．(1)A，B两点关于y轴对称；(2)A，B两点关于x轴对称；(3)AB∥x轴；(4)A，B两点在第二、四象限两坐标轴夹角的平分线上．


20．(8分)如图所示，△ABC在正方形网格中，若点A的坐标为（0，3）C（1，1），按要求回答下列问题：
（1）在图中建立正确的平面直角坐标系；
（2）根据所建立的坐标系，写出点B的坐标；
（3）作出△ABC关于x轴的对称图形△A′B′C′．（不用写作法）






21．(8分)如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A、B?的对应点C，D，连接AC，BD，CD．
（1）求点C，D的坐标及四边形ABDC的面积S四边形ABDC；
（2）在y轴上是否存在一点P，连接PA，PB，使S△PAB=S四边形ABDC？若存在这样一点，求出点P的坐标；若不存在，试说明理由．






22．(8分)如图，四边形ABCD各个顶点的坐标分别为A(－2,8)，B(－11,6)，C(－14,0)，D(0,0)．
(1)求这个四边形的面积？
(2)如果把原来四边形ABCD各个顶点的纵坐标保持不变，横坐标增加2，所得的四边形面积又是多少？
　　　　
　　　　　　　　




23．(10分)已知，△ABC满足BC＝AB，∠ABC＝90°，A点在x轴的负半轴上，直角顶点B在y轴上，点C在x轴上方．
(1)如图1所示，若A的坐标是(－3,0)，点B与原点重合，则点C的坐标是　　　　　　；
(2)如图2，过点C作CD⊥y轴于点D，请判断线段OA，OD，CD之间的数量关系并说明理由；
(3)如图3，若x轴恰好平分∠BAC，BC与x轴交于点E，过点C作CF⊥x轴于点F，问CF与AE有怎样的数量关系？并说明理由．

　　　　　　　












答案
选择题：BDDAC BCDDB
填空题：



或

3，
解答题
17．解：各点的坐标分别为：A(－4,4)，B(－3,0)，C(－2，－2)，D(1，－4)，
E(1，－1)，F(3,0)，G(2,3)，点B和点F关于y轴对称．
18．A′(2,3),B′(1,0),C′(5,1)．

19．解：(1)A，B两点关于y轴对称，故有b＝3，a＝4；
(2)A，B两点关于x轴对称，∴有a＝－4，b＝－3；
(3)AB∥x轴，即b＝3，a为不等于－4的任意实数；
(4)如图所示，根据题意a＋3＝0，b－4＝0，∴a＝－3，b＝4．
20．（1）所建立的平面直角坐标系如下所示：
（2）点B和点C的坐标分别为：B（﹣3，﹣1）；
（3）所作△A'B'C'如下图所示．


21．解：（1）C（0，2），D（4，2），
四边形ABCD的面积=（3+1）×2=8；
（2）假设y轴上存在P（0，b）点，则S△PAB=S四边形ABDC
∴|AB|?|b|=8，
∴b=±4，
∴P（0，4）或P（0，﹣4）．
22．解：(1)将四边形分割成如图所示的长方形、直角三角形，分别为①、②、③、④，共4个部分，可求出各自的面积：S长方形①＝9×6＝54，S直角三角形②＝×2×8＝8，S直角三角形③＝×2×9＝9，S直角三角形④＝×3×6＝9．∴四边形的面积为54＋8＋9＋9＝80．
(2)如果把原来四边形ABCD各个顶点的纵坐标保持不变，横坐标增加2，所得的四边形就是将原来的四边形向右平移两个单位长度得到的，所以其面积不变，还是80．
23．解：(1)(0,3)；
(2)数量关系是：OA＝OD＋CD，理由如下：∵CD⊥y轴，∴∠CDB＝90°，∠DCB＋∠CBD＝90°，∵∠ABC＝90°，∴∠ABO＋∠CBD＝90°，∴∠ABO＝∠DCB．在△ABO和△BCD中，∵
∴△ABO≌△BCD(AAS)，∴BO＝CD，OA＝DB．∵BD＝OB＋OD，∴OA＝CD＋OD；
(3)AE＝2CF，如图，延长CF，AB相交于G，∵x轴恰好平分∠BAC，∴∠CAF＝∠GAF，∵CF⊥x轴，
∴∠AFE＝∠AFG＝90°．在△AFC和△AFG中，∵∴△AFC≌△AFG(ASA)，
∴CF＝GF．∵∠AEB＝∠CEF，∠ABE＝∠CFE＝90°，∴∠BAE＝∠BCG．在△ABE和△CBG中，
∵∴△ABE≌△CBG(ASA)，∴AE＝CG，∴AE＝CF＋GF＝2CF．





第3题图

第13题图 第15题图 第16题图








21世纪教育网 www．21cnjy．com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www．21cnjy．com)