浙教版2019-2020八年级数学上册期末冲刺满分 专题四 图形与坐标(30题含答案)
文档属性
| 名称 | 浙教版2019-2020八年级数学上册期末冲刺满分 专题四 图形与坐标(30题含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-30 18:59:14 | ||
图片预览



文档简介
浙教版2019-2020八年级数学上册期末冲刺满分专题训练四图形与坐标
(30道题)
1.在图所示的平面直角坐标系中表示下面各点:
A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7)。????
(1)A点到原点O的距离是________个单位长。
(2)将点C向左平移6个单位,它会与点________重合。
(3)连接CE,则直线CE与y轴是什么位置关系?
(4)点F到x、y轴的距离分别是多少?
2.如图,正方形ABCD的边长为2
(1)建立一个合适的平面直角坐标系,使得点A在第三象限;
(2)写出点A , B , C,D的坐标.
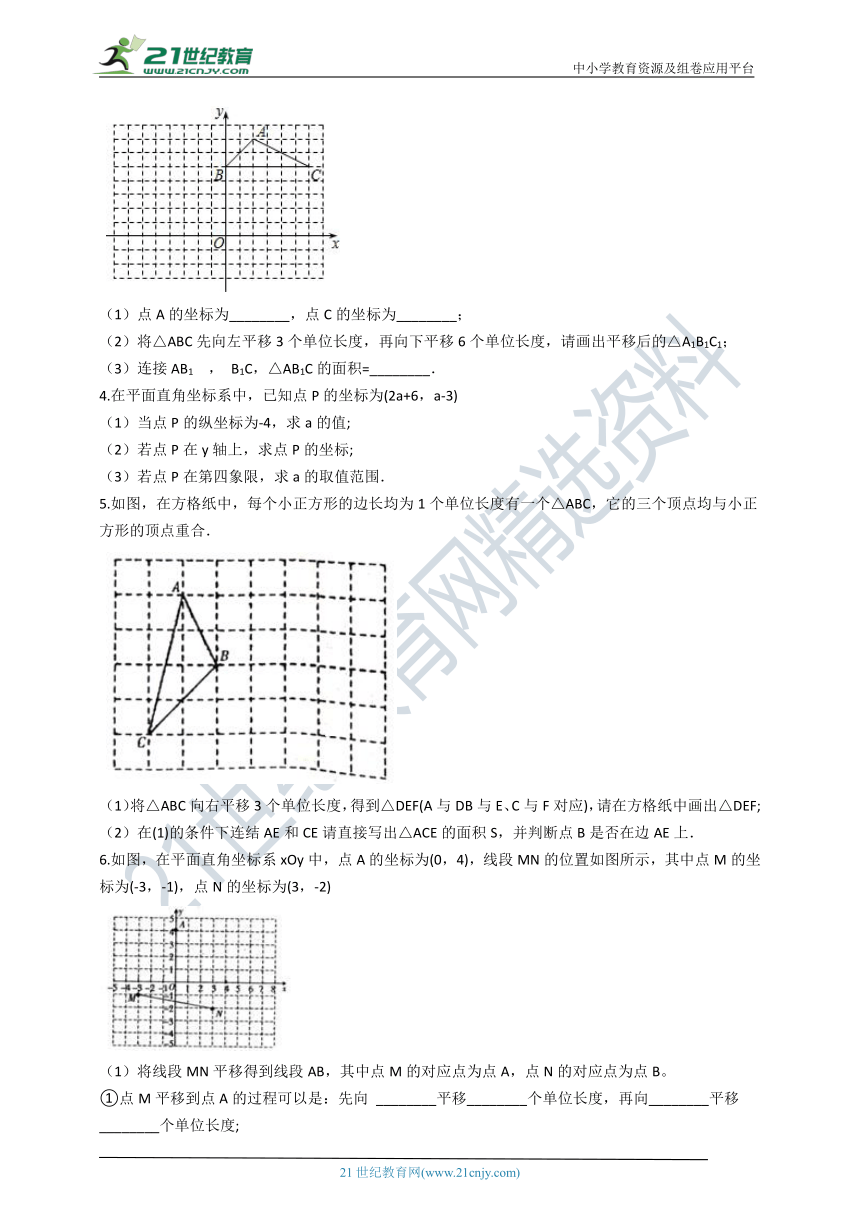
3.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
(1)点A的坐标为________,点C的坐标为________;
(2)将△ABC先向左平移3个单位长度,再向下平移6个单位长度,请画出平移后的△A1B1C1;
(3)连接AB1 , B1C,△AB1C的面积=________.
4.在平面直角坐标系中,已知点P的坐标为(2a+6,a-3)
(1)当点P的纵坐标为-4,求a的值;
(2)若点P在y轴上,求点P的坐标;
(3)若点P在第四象限,求a的取值范围.
5.如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个△ABC,它的三个顶点均与小正方形的顶点重合.
(1)将△ABC向右平移3个单位长度,得到△DEF(A与DB与E、C与F对应),请在方格纸中画出△DEF;
(2)在(1)的条件下连结AE和CE请直接写出△ACE的面积S,并判断点B是否在边AE上.
6.如图,在平面直角坐标系xOy中,点A的坐标为(0,4),线段MN的位置如图所示,其中点M的坐标为(-3,-1),点N的坐标为(3,-2)
(1)将线段MN平移得到线段AB,其中点M的对应点为点A,点N的对应点为点B。
①点M平移到点A的过程可以是:先向 ________平移________个单位长度,再向________平移________个单位长度;
②点B的坐标为________。
(2)在(1)的条件下,若点C的坐标为(4,0),连接AC、BC,画出图形并求△ABC的面积。
7.已知点A(a,0)和B(0,b)满足(a-4)2+|b-6|=0,分别过点A、B作x轴、y轴的垂线交于点C,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动
(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,直接写出点P的坐标
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B‘P’,若B‘P’将四边形OACB的面积分成相等的两部分,求h的值.
8.对于实数a,b定义两种新运算“※”和“*”:a※b=a+kb,a*b=ka+b(其中k为常数,且k≠0),若对于平面直角坐标系xOy中的点P(a,b),有点P′的坐标(a※b,a*b)与之对应,则称点P的“k衍生点”为点P′.例如:P(1,3)的“2衍生点”为P′(1+2×3,2×1+3),即P′(7,5).
(1)点P(﹣1,5)的“3衍生点”的坐标为________;
(2)若点P的“5衍生点”P的坐标为(9,﹣3),求点P的坐标;
(3)若点P的“k衍生点”为点P′,且直线PP′平行于y轴,线段PP′的长度为线段OP长度的3倍,求k的值.
9.如图,Rt△AOB?在平面直角坐标系中,点O与坐标原点重合,点A在x轴上,点B在y轴上, ,将△AOB沿直线BE折叠,使得OB边落在AB上,点O与点D重合.
(1)求直线BE的解析式;
(2)求点D的坐标;
(3)x轴上是否存在点P,使△PAD为等腰三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由。
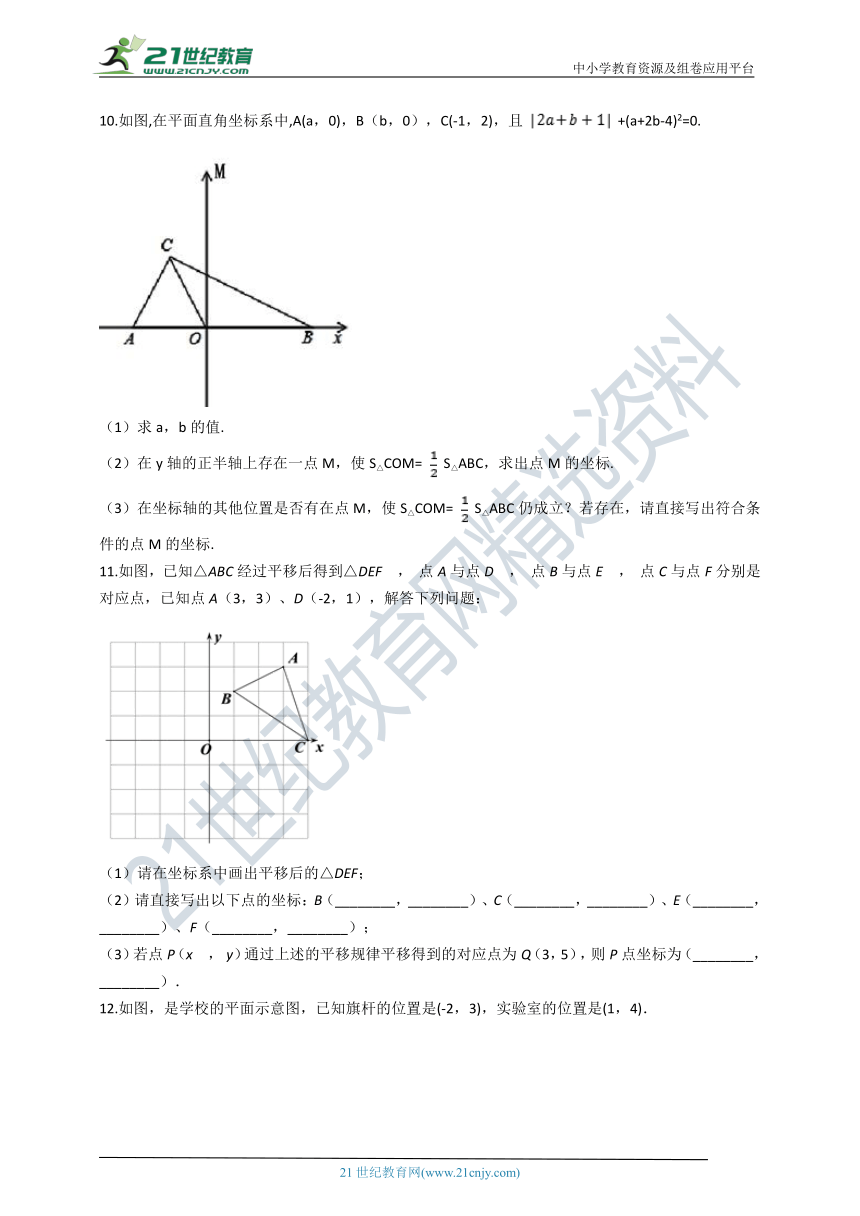
10.如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且 +(a+2b-4)2=0.
(1)求a,b的值.
(2)在y轴的正半轴上存在一点M,使S△COM= S△ABC,求出点M的坐标.
(3)在坐标轴的其他位置是否有在点M,使S△COM= S△ABC仍成立?若存在,请直接写出符合条件的点M的坐标.
11.如图,已知△ABC经过平移后得到△DEF , 点A与点D , 点B与点E , 点C与点F分别是对应点,已知点A(3,3)、D(-2,1),解答下列问题:
(1)请在坐标系中画出平移后的△DEF;
(2)请直接写出以下点的坐标:B(________,________)、C(________,________)、E(________,________)、F(________,________);
(3)若点P(x , y)通过上述的平移规律平移得到的对应点为Q(3,5),则P点坐标为(________,________).
12.如图,是学校的平面示意图,已知旗杆的位置是(-2,3),实验室的位置是(1,4).
(1)画出相应的平面直角坐标系;
(2)在图中分别写出食堂、图书馆的位置;
(3)已知办公楼的位置是(-2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;
(4)如果一个单位长度表示30米,请求出宿舍楼到教学棱的实际距离.
13.如图,在平面直角坐标系中,已知A(0,5),? B(a,b),且a,b满足b= + -1.
(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
14.如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).
(1)在平面直角坐标系中画出△ABC,则此△ABC的面积是?? ▲??? ;
(2)若点D与点C关于y轴对称,则点D的坐标为________;
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
15.如图,直线MN与x轴、y轴分别相交于B、A两点,OA,OB的长满足式子
(1)求A,B两点的坐标;
(2)若点O到AB的距离为 ,求线段AB的长;
(3)在(2)的条件下。x轴上是否存在点p使 以AB为等腰三角形,若存在,请直接写出满足条件的点p的坐标。
16.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,1),C(-1,2).
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1;
(2)请直接写出点C关于y轴的对称点C'的坐标:????????????? ;
(3)△ABC的面积=________;
(4)在y轴上找一点P,使得△PAC周长最小,并求出△PAC周长的最小值.
17.如图,在平面直角坐标系中,直线 是第一、三象限的角平分线.
(1)由图观察易知A(0,2)关于直线的对称点 的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B'、C'?的位置,并写出他们的坐标;
(2)结合图形观察以上三组点的坐标,直接写出坐标面内任一点P 关于第一、三象限的角平分线 的对称点 的坐标为________.
(3)已知两点D(1,-3)、E(-1,-4),试在直线 上画出点Q,使△QDE的周长最小,并求△QDE周长的最小值.
18.如图1,点A(2,1),点A与点B关于y轴对称,AC∥y轴,且AC=3,连接BC交y轴于点D.
(1)点B的坐标为________,点C的坐标为________;
(2)如图2,连接OC,OC平分∠ACB,求证:OB⊥OC;
(3)如图3,在(2)的条件下,点P为OC上一点,且∠PAC=45°,求点P的坐标.
19.如图,△ABC的三个顶点在边长为1的正方形网格中,已知A(﹣1,﹣1),B(4,﹣1),C(3,1).
(1)画出△ABC及关于y轴对称的△A1B1C1;
(2)写出点A的对应点A1的坐标,点B的对应点B1的坐标,点C的对应点C1的坐标;
(3)请直接写出以AB为边且与△ABC全等的三角形的第三个顶点(不与C重合)的坐标.
20.如图所示,四边形 ABCD , ∠A=90°,AB=3m , BC=12m , CD=13m , DA=4m .
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD= S四边形ABCD , 求 P的坐标.
21.已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
22.如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0)、C(0,2),点B在第一象限.
(1)写出点B的坐标;
(2)若过点C的直线交长方形的OA边于点D,且把长方形OABC的周长分成2∶3的两部分,求点D的坐标;
(3)如果将(2)中的线段CD向下平移3个单位长度,得到对应线段C′D′,在平面直角坐标系中画出△CD′C′,并求出它的面积。
23.在平面直角坐标系中,A(﹣2,0),C(2,2),过C作CB⊥x轴于B.
(1)如图1,△ABC的面积是________;
(2)如图1,在y轴上找一点P,使得△ABP的面积与△ABC的面积相等,请直接写出P点坐标:________;
(3)如图2,若过B作BD∥AC交y轴于D,则∠BAC+∠ODB的度数为________度;
(4)如图3,BD∥AC,若AE、DE分别平分∠CAB,∠ODB,求∠AED的度数.
24.如图,在平面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,
(1)求三角形ABC的面积;
(2)如果在第二象限内有一点P(m, ),请用含m的式子表示四边形ABOP的面积.
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
25.如图是小丽以学校为观测点,画出的一张平面图.
(1)生源大酒店在学校________偏________方向________米处.汽车站在学校________偏________方向________米处;
(2)中医院在邮电局东偏北60°方向400米处,请在上图中标出它的位置;
(3)小丽以每分钟50米的速度步行,从汽车站经过学校.邮局再到中医院大约需要________分钟.
26.如图,在平面直角坐标系中,已知点A(﹣2,0),B(0,3),O为原点.
(1)求三角形AOB的面积;
(2)将线段AB沿x轴向右平移4个单位,得线段A′B′,坐标轴上有一点C满足三角形A′B′C的面积为9,求点C的坐标.
27.如图所示,在平面内有四个点,它们的坐标分别是A(﹣1,0),B(2+ ,0),C(2,1),D(0,1).
(1)依次连结A、B、C、D,围成的四边形是一个________形;
(2)求这个四边形的面积;
(3)将这个四边形向左平移 个单位长度,四个顶点的坐标分别为多少?
28.如图所示,△ABC的顶点分别为A(-4, 5),B(﹣3, 2),C(4,-1).
(1)作出△ABC关于x轴对称的图形△A1B1C1;
(2)写出A1、B1、C1的坐标;
(3)若AC=10,求△ABC的AC边上的高.
29.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标________,点B1的坐标________;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标________.
30.在边长为1的小正方形网格中,△ABC的顶点均在格点上,
(1)B点关于y轴的对称点坐标为________;
(2)将△ABC向右平移3个单位长度得到△A1B1C1 , 请画出△A1B1C1;
(3)在(2)的条件下,A1的坐标为________;
(4)求△ABC的面积.
答案
1. (1)3 (2)D (3)解:连结CE,易知C、E点坐标关于x轴对应数值相等。故CE平行于y轴。 (4)解:点F分别到x、y轴的距离是7和5
2. (1)解:如图所示:
(2)解:点A、B、C、D的坐标分别为(﹣2,﹣2),(0,﹣2),(0,0),(﹣2,0).
3. (1)(2,7);(6,5) (2)解:△A1B1C1如图所示;
(3)21
4. (1)解:
解得:
(2)解:若点 在 轴上,则
∴
∴若点 在 轴上,点 的坐标为(0,-6)
(3)解:若点 在第四象限,则
解得:
5. (1)解:如答图所示,
(2)解:由图可知:s=5×4- ×4×1- ×2×4- ×2×5=20-2-4-5=9
根据图形可知,点B不在边AE上
6. (1)右;3;上;5(或上、5、右、3);(6,3) (2)解:如图,S△ABC=6×4- ×4×4- ×2×3- ×6×1=10
7. (1)解:∵ ,
∴ 且 ,解得 , ,
∴点 、 的坐标分别为(4,0)和(0,6),
∴点 的坐标为(4,6)
(2)解:点 的坐标为(4,4) (3)解:如图所示,将线段 向下平移 个单位,
则 , , , ?
当 将四边形 的面积分成相等的两部分,则
∴
即当 时, 平分四边形 的面积
8. (1)(14,2) (2)解:设P(x,y)
依题意,得方程组 .
解得 .
∴点P(﹣1,2)
(3)解:设P(a,b),则P′的坐标为(a+kb,ka+b).
∵PP′平行于y轴
∴a=a+kb,即kb=0,
又∵k≠0,
∴b=0.
∴点P的坐标为(a,0),点P'的坐标为(a,ka),
∴线段PP′的长度为|ka|.
∴线段OP的长为|a|.
根据题意,有|PP′|=3|OP|,
∴|ka|=3|a|.
∴k=±3.
9. (1)解:∵OB= ,AO=6,∴AB= = ,∴∠BAO=30°,∴∠ABO=60°.
∵沿BE折叠O、D重合,∴∠EBO=30°,OE= BE,设OE=x,则(2x)2=x2+ ,∴x=2,即 BE=4,E(﹣2,0),设y=kx+b代入得: ,解得: ,∴直线BE的解析式是:
(2)解:过D作DG⊥OA于G.
∵沿BE折叠O、D重合,∴DE=2.
∵∠DAE=30°,∴∠DEA=60°,∠ADE=∠BOE=90°,∴∠EDG=30°,∴GE=1,DG= ,∴OG=1+2=3,∴D的坐标是:D
(3)解:设P(x,0).
∵∠OAB=30°,DG= ,∴AD=2DG= .分三种情况讨论:
①以A为圆心,AD为半径作圆与x轴交于点P,则AP=AD= ,∴P( ,0);
②以D为圆心,DA为半径作圆与x轴交于点P,则AP=2AG= DG=6.
∵OA=6,∴P与O重合,∴P(0,0);
③设线段AD的垂直平分线交x轴于P,则PA=PD,∴ ,解得:x=-4,∴P(-4,0).
综上所述:P的坐标为:P( ,0)或P(0,0)或P(-4,0).
10. (1)解:由题意得, ,
①×2得,4a+2b+2=0③,
③?②得,3a=?6,
解得a=?2,
把a=?2代入①得,?4+b+1=0,
解得b=3
(2)解:∵a=?2,b=3,C(?1,2),
∴AB=3?(?2)=5,点C到y轴的距离为1,
∴ OM?1= × ×5×2,
解得OM=5,
∵点M在y轴正半轴上,
∴M的坐标为(0,5)
(3)解:存在.
点M在y轴负半轴上时,点M(0,-5),
点M在x轴上时, OM?2= × ×5×2,
解得OM=2.5,
所以,点M的坐标为(-2.5,0)或(2.5,0),
综上所述,存在点M的坐标为(0,-5)或(-2.5,0)或(2.5,0).
11. (1)解:如图所示,
(2)1;2;4;0;-4;0;-1;-2 (3)8;7
12. (1)如图, (2)答:食堂(-5,5),图书馆(2,5) (3)如图, (4)解:∵ 宿舍楼(-6,2)到教学楼(2,2) ∴宿舍楼到教学楼的实际距离为:30×|-6-2|=240米
13.(1)解:∵b= + -1
∴a=4 ,b= -1
∴B点坐标为:(4,-1)
∵A(0,5)
∴AB= )
(2)解:∵直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°
∴直线CD平行于y= -x
设直线CD解析式为y= -x +b
则B点坐标为(b,0)
把点P(m,n)代入得:n= -m +b
∴b= m+n
∴OP2-OC2=
∵mn=-6
∴OP2-OC2
(3)解:取点D关于y轴的对称点 ,则∠DAO=∠ ,
∴∠DAO +∠BAO=∠ +∠BAO=∠BA
∵点D(1,0)
∴ (-1,0)
由(1)得:A(0,5),B(4,-1)
∴A = , ,
∴A ?,
∴△A 是等腰直角三角形
∴∠DAO +∠BAO=∠BA =45°
14. (1); S△ABC=S梯形ADEC-S△ADB-S△BEC =(3+1)×4÷2-2×1÷2-2×3÷2 =8-1-3 =4 (2)(-4,3) (3)设点P的坐标为(t,0) ∴|2-t|×1÷2=4 ∴|2-t|=8 ∴t=-6或t=10 ∴点P的坐标为(-6,0)和(10,0)
15. (1)由?得:OA=6,OB=8 ∴A(0,6)、B(8,0) (2)∵∠AOB=90°, ∴AB===10 (3)解:存在(-8,0)、(-2,0)、(18,0)
16. (1)解:如图所示,△A1B1C1即为所求.
(2)(1,2) (3)4 (4)解:如图,作点C关于y轴的对称点C′,连接AC′交y轴于点P,P即为所求,此时PA+PC最小,
∵PA+PC=PA+PC′=AC′= ,AC= ,
∴△PAC周长的最小值为
17. (1)B'(3,5),C'(5,-2) (2) (3)先作出点D关于直线l的对称点D',连接D'E与直线l的交点即为点Q, ∵点D坐标(1,-3), ∴点D'坐标(-3,1) 又∵点E坐标(-1,-4), ∴直线D'E的表达式为y=, 联合解得y=x= , ∴点Q的坐标(- , -) ∴C△QDE=QE+QD+DE=QE+QD'+DE=ED'+DE= , 即点Q坐标(- , -), ∴△QDE的周长最小值为。
18. (1)(-2,1);(2,4) (2)解:∵OC平分∠ACB,
∴∠1=∠2,
∵AC∥y轴,
∴∠3=∠2,
∴∠1=∠3,
∴CD=DO.
作CE⊥y轴于点E,连接AB交y轴于点F,
∵点A,点B关于y轴对称,
∴BF⊥y轴,
∴∠CED=∠BFD,
∵B(-2,1),C(2,4),
∴CE=BF=2,
在△CDE和△BDF中,
DCED=DBFDDCDE=DBDF,CE=BF,
∴△CDE≌△BDF(AAS).
∴CD=BD,
∴BD=CD=OD,
∴∠DBO=∠DOB,
∵∠1+∠3+∠DBO+∠DOB=180°,
∴∠3+∠DOB=90°,
∴OB⊥OC
(3)解:连接BP,作PQ⊥x轴于点Q,
∵点A,点B关于y轴对称,
∴AB⊥y轴,
∴∠BAC=90°,
∵∠PAC=45°,
∴PA平分∠CAB,
∵OC平分∠ACB,
∴BP平分∠ABC.
∴∠BPC=135°,
∴∠BPO=45°.
∵∠BOP=90°,
∴OB=OP,
在△BOF和△POQ中,
DBFO=DPQO,DBOF=DPOQ,OB=OP,
∴△BOF≌△POQ(AAS).
∴PQ=BF=2,OQ=OF=1,
∴P(1,2).
19. (1)解:画图如图所示:
(2)解:由图可得,点A1的坐标是(1,﹣1),点B1的坐标是(﹣4,﹣1),点C1的坐标是(﹣3,1) (3)解:∵AB为公共边,
∴与△ABC全等的三角形的第三个顶点的坐标为(0,﹣3),(0,1)或(3,﹣3)
20. (1)证明:连接 BD .
∵AD=4m , AB=3m , ∠BAD=90°,
∴BD=5m .
又∵BC=12m , CD=13m ,
∴BD2+BC2=CD2 .
∴BD⊥CB
(2)解:四边形 ABCD 的面积=△ABD 的面积+△BCD 的面积
= ?×3×4+ ×12×5
=6+30
=36(m2).
故这块土地的面积是 36m2
(3)解:∵S△PBD= S 四边形ABCD
∴ ?PD?AB= ?×36, ∴ ?PD×3=9,
∴PD=6,
∵D(0,4),点 P 在 y 轴上,
∴P 的坐标为(0,-2)或(0,10).
21. (1)解:1﹣a=﹣3,a=4 (2)解:由a=4得:2a﹣12=2×4﹣12=﹣4,又点Q(x,y)位于第二象限,所以y>0;
取y=1,得点Q的坐标为(﹣4,1)
(3)解:因为点P(2a﹣12,1﹣a)位于第三象限,
所以 ,
解得:1<a<6.
因为点P的横、纵坐标都是整数,所以a=2或3或4或5;
当a=2时,1﹣a=﹣1,所以PQ>1;
当a=3时,1﹣a=﹣2,所以PQ>2;
当a=4时,1﹣a=﹣3,所以PQ>3;
当a=5时,1﹣a=﹣4,所以PQ>4.
22.【答案】(1)解:点B的坐标(3,2);
(2)解:长方形OABC周长=2×(2+3)=10,
∵长方形OABC的周长分成2:3的两部分,
∴两个部分的周长分别为4,6,
∵点C的坐标是(0,2),点D在边OA上,
∴OD=2,
∴点D的坐标为(2,0)
(3)解:如图所示,△CD′C′即为所求作的三角形,
CC′=3,点D′到CC′的距离为2,
所以,△CD′C′的面积= ×3×2=3
23. (1)4 (2)(0,2)或(0,-2) (3)90 (4)解:连接AD,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠EAO= ∠BAC, ∠EDO= ∠ODB,
∴∠EAO+∠EDO= (∠BAC+∠ODB=45°,
∵∠AED+∠EAD+∠EDA=180° , 即∠AED+∠EAO+∠OAD+∠EDO+∠ODA=180°,
∵∠OAD+∠ODA=90°,
∴∠AED+45°+90°=180°,
∴∠AED=45°.
24.(1)解:已知点A(0,2),B(3,0),C(3,4), 过A点作BC边上的高,交BC于点H, 则三角形ABC的面积为:S= BC?AH= ×4×3=6 (2)解:四边形ABOP的面积可以看作是△APO和△AOB的面积和, ∵P在第二象限,∴m<0,SAPOB=S△AOB+SAPO= + ×(﹣m)×2=3﹣m. 故四边形ABOP的面积为3﹣m (3)解:当四边形ABOP的面积与△ABC的面积相等时, 即3﹣m=6,得m=﹣3, 此时P点坐标为:(﹣3, ), 存在P点,使四边形ABOP的面积与△ABC的面积相等.
25.(1)北;西30°;400;南;西50°;600 (2)解:因为400米=40000厘米,
则中医院到邮电局的图上距离是:40000× =2(厘米);
如图所示,即为中医院的位置:
(3)24
26.(1)解:∵点A(﹣2,0),B(0,3), ∴OA=2,OB=3, ∴△AOB的面积= ×2×3=3 (2)解:由平移得,A′(2,0),B′(4,3), 当C在x轴上时,则S△A′B′C= A′C?3=9, ∴A′C=6, 设C(x,0),则有|x+2|=6, ∴x=﹣4,x=8, ∴C(﹣4,0)或(8,0); 当C在y轴的正半轴上时,设C(0,y),则S△A′B′C= ?[4(3+y)﹣2y﹣3×3]=9, 解得:y=6, 当C在y轴的负半轴上时,设C(0,y),则S△A′B′C= ?[4(3﹣y)+2y﹣3×3]=9, 解得:y=﹣12, ∴C(0,9)或(0,﹣12), 综上所述,C((﹣4,0)或(8,0)或(0,9)或(0,﹣12)
27.(1)梯 (2)解:∵A(﹣1,0),B(2+ ,0),C(2,1),D(0,1),
∴AB=3+ ,CD=2,
∴四边形ABCD的面积= (AB+CD)?OD= (3+ )×1= (3)解:A′(﹣1﹣ ,0),B′(2,0),C′(2﹣ ,1),D′(﹣ ,1)
28.(1)解:如图所示,△A1B1C1即为所求。 (2)解:A1(-4, -5),B1(﹣3,- 2),C1(4,1) (3)解:? 由图可得S△ABC=6×8×-1×3×-1×3-3×7×=9 又AC==10 ∵AC×h=S△ABC ∴h=9×2÷10=1.8 所以△ABC的AC边上的高为1.8
29. (1) (2)(2,-1);(-1,-3) (3)(4, 2)或(-4,-6)
30.(1)(2,2) (2)解:如图所示:△A1B1C1 , 即为所求 (3)(3,4) (4)解:△ABC的面积为:2×3﹣ ×2×2﹣ ×1×1﹣ ×1×3=2
(30道题)
1.在图所示的平面直角坐标系中表示下面各点:
A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7)。????
(1)A点到原点O的距离是________个单位长。
(2)将点C向左平移6个单位,它会与点________重合。
(3)连接CE,则直线CE与y轴是什么位置关系?
(4)点F到x、y轴的距离分别是多少?
2.如图,正方形ABCD的边长为2
(1)建立一个合适的平面直角坐标系,使得点A在第三象限;
(2)写出点A , B , C,D的坐标.
3.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
(1)点A的坐标为________,点C的坐标为________;
(2)将△ABC先向左平移3个单位长度,再向下平移6个单位长度,请画出平移后的△A1B1C1;
(3)连接AB1 , B1C,△AB1C的面积=________.
4.在平面直角坐标系中,已知点P的坐标为(2a+6,a-3)
(1)当点P的纵坐标为-4,求a的值;
(2)若点P在y轴上,求点P的坐标;
(3)若点P在第四象限,求a的取值范围.
5.如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个△ABC,它的三个顶点均与小正方形的顶点重合.
(1)将△ABC向右平移3个单位长度,得到△DEF(A与DB与E、C与F对应),请在方格纸中画出△DEF;
(2)在(1)的条件下连结AE和CE请直接写出△ACE的面积S,并判断点B是否在边AE上.
6.如图,在平面直角坐标系xOy中,点A的坐标为(0,4),线段MN的位置如图所示,其中点M的坐标为(-3,-1),点N的坐标为(3,-2)
(1)将线段MN平移得到线段AB,其中点M的对应点为点A,点N的对应点为点B。
①点M平移到点A的过程可以是:先向 ________平移________个单位长度,再向________平移________个单位长度;
②点B的坐标为________。
(2)在(1)的条件下,若点C的坐标为(4,0),连接AC、BC,画出图形并求△ABC的面积。
7.已知点A(a,0)和B(0,b)满足(a-4)2+|b-6|=0,分别过点A、B作x轴、y轴的垂线交于点C,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动
(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,直接写出点P的坐标
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B‘P’,若B‘P’将四边形OACB的面积分成相等的两部分,求h的值.
8.对于实数a,b定义两种新运算“※”和“*”:a※b=a+kb,a*b=ka+b(其中k为常数,且k≠0),若对于平面直角坐标系xOy中的点P(a,b),有点P′的坐标(a※b,a*b)与之对应,则称点P的“k衍生点”为点P′.例如:P(1,3)的“2衍生点”为P′(1+2×3,2×1+3),即P′(7,5).
(1)点P(﹣1,5)的“3衍生点”的坐标为________;
(2)若点P的“5衍生点”P的坐标为(9,﹣3),求点P的坐标;
(3)若点P的“k衍生点”为点P′,且直线PP′平行于y轴,线段PP′的长度为线段OP长度的3倍,求k的值.
9.如图,Rt△AOB?在平面直角坐标系中,点O与坐标原点重合,点A在x轴上,点B在y轴上, ,将△AOB沿直线BE折叠,使得OB边落在AB上,点O与点D重合.
(1)求直线BE的解析式;
(2)求点D的坐标;
(3)x轴上是否存在点P,使△PAD为等腰三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由。
10.如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且 +(a+2b-4)2=0.
(1)求a,b的值.
(2)在y轴的正半轴上存在一点M,使S△COM= S△ABC,求出点M的坐标.
(3)在坐标轴的其他位置是否有在点M,使S△COM= S△ABC仍成立?若存在,请直接写出符合条件的点M的坐标.
11.如图,已知△ABC经过平移后得到△DEF , 点A与点D , 点B与点E , 点C与点F分别是对应点,已知点A(3,3)、D(-2,1),解答下列问题:
(1)请在坐标系中画出平移后的△DEF;
(2)请直接写出以下点的坐标:B(________,________)、C(________,________)、E(________,________)、F(________,________);
(3)若点P(x , y)通过上述的平移规律平移得到的对应点为Q(3,5),则P点坐标为(________,________).
12.如图,是学校的平面示意图,已知旗杆的位置是(-2,3),实验室的位置是(1,4).
(1)画出相应的平面直角坐标系;
(2)在图中分别写出食堂、图书馆的位置;
(3)已知办公楼的位置是(-2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;
(4)如果一个单位长度表示30米,请求出宿舍楼到教学棱的实际距离.
13.如图,在平面直角坐标系中,已知A(0,5),? B(a,b),且a,b满足b= + -1.
(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
14.如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).
(1)在平面直角坐标系中画出△ABC,则此△ABC的面积是?? ▲??? ;
(2)若点D与点C关于y轴对称,则点D的坐标为________;
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
15.如图,直线MN与x轴、y轴分别相交于B、A两点,OA,OB的长满足式子
(1)求A,B两点的坐标;
(2)若点O到AB的距离为 ,求线段AB的长;
(3)在(2)的条件下。x轴上是否存在点p使 以AB为等腰三角形,若存在,请直接写出满足条件的点p的坐标。
16.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,1),C(-1,2).
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1;
(2)请直接写出点C关于y轴的对称点C'的坐标:????????????? ;
(3)△ABC的面积=________;
(4)在y轴上找一点P,使得△PAC周长最小,并求出△PAC周长的最小值.
17.如图,在平面直角坐标系中,直线 是第一、三象限的角平分线.
(1)由图观察易知A(0,2)关于直线的对称点 的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B'、C'?的位置,并写出他们的坐标;
(2)结合图形观察以上三组点的坐标,直接写出坐标面内任一点P 关于第一、三象限的角平分线 的对称点 的坐标为________.
(3)已知两点D(1,-3)、E(-1,-4),试在直线 上画出点Q,使△QDE的周长最小,并求△QDE周长的最小值.
18.如图1,点A(2,1),点A与点B关于y轴对称,AC∥y轴,且AC=3,连接BC交y轴于点D.
(1)点B的坐标为________,点C的坐标为________;
(2)如图2,连接OC,OC平分∠ACB,求证:OB⊥OC;
(3)如图3,在(2)的条件下,点P为OC上一点,且∠PAC=45°,求点P的坐标.
19.如图,△ABC的三个顶点在边长为1的正方形网格中,已知A(﹣1,﹣1),B(4,﹣1),C(3,1).
(1)画出△ABC及关于y轴对称的△A1B1C1;
(2)写出点A的对应点A1的坐标,点B的对应点B1的坐标,点C的对应点C1的坐标;
(3)请直接写出以AB为边且与△ABC全等的三角形的第三个顶点(不与C重合)的坐标.
20.如图所示,四边形 ABCD , ∠A=90°,AB=3m , BC=12m , CD=13m , DA=4m .
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD= S四边形ABCD , 求 P的坐标.
21.已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
22.如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0)、C(0,2),点B在第一象限.
(1)写出点B的坐标;
(2)若过点C的直线交长方形的OA边于点D,且把长方形OABC的周长分成2∶3的两部分,求点D的坐标;
(3)如果将(2)中的线段CD向下平移3个单位长度,得到对应线段C′D′,在平面直角坐标系中画出△CD′C′,并求出它的面积。
23.在平面直角坐标系中,A(﹣2,0),C(2,2),过C作CB⊥x轴于B.
(1)如图1,△ABC的面积是________;
(2)如图1,在y轴上找一点P,使得△ABP的面积与△ABC的面积相等,请直接写出P点坐标:________;
(3)如图2,若过B作BD∥AC交y轴于D,则∠BAC+∠ODB的度数为________度;
(4)如图3,BD∥AC,若AE、DE分别平分∠CAB,∠ODB,求∠AED的度数.
24.如图,在平面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,
(1)求三角形ABC的面积;
(2)如果在第二象限内有一点P(m, ),请用含m的式子表示四边形ABOP的面积.
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
25.如图是小丽以学校为观测点,画出的一张平面图.
(1)生源大酒店在学校________偏________方向________米处.汽车站在学校________偏________方向________米处;
(2)中医院在邮电局东偏北60°方向400米处,请在上图中标出它的位置;
(3)小丽以每分钟50米的速度步行,从汽车站经过学校.邮局再到中医院大约需要________分钟.
26.如图,在平面直角坐标系中,已知点A(﹣2,0),B(0,3),O为原点.
(1)求三角形AOB的面积;
(2)将线段AB沿x轴向右平移4个单位,得线段A′B′,坐标轴上有一点C满足三角形A′B′C的面积为9,求点C的坐标.
27.如图所示,在平面内有四个点,它们的坐标分别是A(﹣1,0),B(2+ ,0),C(2,1),D(0,1).
(1)依次连结A、B、C、D,围成的四边形是一个________形;
(2)求这个四边形的面积;
(3)将这个四边形向左平移 个单位长度,四个顶点的坐标分别为多少?
28.如图所示,△ABC的顶点分别为A(-4, 5),B(﹣3, 2),C(4,-1).
(1)作出△ABC关于x轴对称的图形△A1B1C1;
(2)写出A1、B1、C1的坐标;
(3)若AC=10,求△ABC的AC边上的高.
29.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标________,点B1的坐标________;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标________.
30.在边长为1的小正方形网格中,△ABC的顶点均在格点上,
(1)B点关于y轴的对称点坐标为________;
(2)将△ABC向右平移3个单位长度得到△A1B1C1 , 请画出△A1B1C1;
(3)在(2)的条件下,A1的坐标为________;
(4)求△ABC的面积.
答案
1. (1)3 (2)D (3)解:连结CE,易知C、E点坐标关于x轴对应数值相等。故CE平行于y轴。 (4)解:点F分别到x、y轴的距离是7和5
2. (1)解:如图所示:
(2)解:点A、B、C、D的坐标分别为(﹣2,﹣2),(0,﹣2),(0,0),(﹣2,0).
3. (1)(2,7);(6,5) (2)解:△A1B1C1如图所示;
(3)21
4. (1)解:
解得:
(2)解:若点 在 轴上,则
∴
∴若点 在 轴上,点 的坐标为(0,-6)
(3)解:若点 在第四象限,则
解得:
5. (1)解:如答图所示,
(2)解:由图可知:s=5×4- ×4×1- ×2×4- ×2×5=20-2-4-5=9
根据图形可知,点B不在边AE上
6. (1)右;3;上;5(或上、5、右、3);(6,3) (2)解:如图,S△ABC=6×4- ×4×4- ×2×3- ×6×1=10
7. (1)解:∵ ,
∴ 且 ,解得 , ,
∴点 、 的坐标分别为(4,0)和(0,6),
∴点 的坐标为(4,6)
(2)解:点 的坐标为(4,4) (3)解:如图所示,将线段 向下平移 个单位,
则 , , , ?
当 将四边形 的面积分成相等的两部分,则
∴
即当 时, 平分四边形 的面积
8. (1)(14,2) (2)解:设P(x,y)
依题意,得方程组 .
解得 .
∴点P(﹣1,2)
(3)解:设P(a,b),则P′的坐标为(a+kb,ka+b).
∵PP′平行于y轴
∴a=a+kb,即kb=0,
又∵k≠0,
∴b=0.
∴点P的坐标为(a,0),点P'的坐标为(a,ka),
∴线段PP′的长度为|ka|.
∴线段OP的长为|a|.
根据题意,有|PP′|=3|OP|,
∴|ka|=3|a|.
∴k=±3.
9. (1)解:∵OB= ,AO=6,∴AB= = ,∴∠BAO=30°,∴∠ABO=60°.
∵沿BE折叠O、D重合,∴∠EBO=30°,OE= BE,设OE=x,则(2x)2=x2+ ,∴x=2,即 BE=4,E(﹣2,0),设y=kx+b代入得: ,解得: ,∴直线BE的解析式是:
(2)解:过D作DG⊥OA于G.
∵沿BE折叠O、D重合,∴DE=2.
∵∠DAE=30°,∴∠DEA=60°,∠ADE=∠BOE=90°,∴∠EDG=30°,∴GE=1,DG= ,∴OG=1+2=3,∴D的坐标是:D
(3)解:设P(x,0).
∵∠OAB=30°,DG= ,∴AD=2DG= .分三种情况讨论:
①以A为圆心,AD为半径作圆与x轴交于点P,则AP=AD= ,∴P( ,0);
②以D为圆心,DA为半径作圆与x轴交于点P,则AP=2AG= DG=6.
∵OA=6,∴P与O重合,∴P(0,0);
③设线段AD的垂直平分线交x轴于P,则PA=PD,∴ ,解得:x=-4,∴P(-4,0).
综上所述:P的坐标为:P( ,0)或P(0,0)或P(-4,0).
10. (1)解:由题意得, ,
①×2得,4a+2b+2=0③,
③?②得,3a=?6,
解得a=?2,
把a=?2代入①得,?4+b+1=0,
解得b=3
(2)解:∵a=?2,b=3,C(?1,2),
∴AB=3?(?2)=5,点C到y轴的距离为1,
∴ OM?1= × ×5×2,
解得OM=5,
∵点M在y轴正半轴上,
∴M的坐标为(0,5)
(3)解:存在.
点M在y轴负半轴上时,点M(0,-5),
点M在x轴上时, OM?2= × ×5×2,
解得OM=2.5,
所以,点M的坐标为(-2.5,0)或(2.5,0),
综上所述,存在点M的坐标为(0,-5)或(-2.5,0)或(2.5,0).
11. (1)解:如图所示,
(2)1;2;4;0;-4;0;-1;-2 (3)8;7
12. (1)如图, (2)答:食堂(-5,5),图书馆(2,5) (3)如图, (4)解:∵ 宿舍楼(-6,2)到教学楼(2,2) ∴宿舍楼到教学楼的实际距离为:30×|-6-2|=240米
13.(1)解:∵b= + -1
∴a=4 ,b= -1
∴B点坐标为:(4,-1)
∵A(0,5)
∴AB= )
(2)解:∵直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°
∴直线CD平行于y= -x
设直线CD解析式为y= -x +b
则B点坐标为(b,0)
把点P(m,n)代入得:n= -m +b
∴b= m+n
∴OP2-OC2=
∵mn=-6
∴OP2-OC2
(3)解:取点D关于y轴的对称点 ,则∠DAO=∠ ,
∴∠DAO +∠BAO=∠ +∠BAO=∠BA
∵点D(1,0)
∴ (-1,0)
由(1)得:A(0,5),B(4,-1)
∴A = , ,
∴A ?,
∴△A 是等腰直角三角形
∴∠DAO +∠BAO=∠BA =45°
14. (1); S△ABC=S梯形ADEC-S△ADB-S△BEC =(3+1)×4÷2-2×1÷2-2×3÷2 =8-1-3 =4 (2)(-4,3) (3)设点P的坐标为(t,0) ∴|2-t|×1÷2=4 ∴|2-t|=8 ∴t=-6或t=10 ∴点P的坐标为(-6,0)和(10,0)
15. (1)由?得:OA=6,OB=8 ∴A(0,6)、B(8,0) (2)∵∠AOB=90°, ∴AB===10 (3)解:存在(-8,0)、(-2,0)、(18,0)
16. (1)解:如图所示,△A1B1C1即为所求.
(2)(1,2) (3)4 (4)解:如图,作点C关于y轴的对称点C′,连接AC′交y轴于点P,P即为所求,此时PA+PC最小,
∵PA+PC=PA+PC′=AC′= ,AC= ,
∴△PAC周长的最小值为
17. (1)B'(3,5),C'(5,-2) (2) (3)先作出点D关于直线l的对称点D',连接D'E与直线l的交点即为点Q, ∵点D坐标(1,-3), ∴点D'坐标(-3,1) 又∵点E坐标(-1,-4), ∴直线D'E的表达式为y=, 联合解得y=x= , ∴点Q的坐标(- , -) ∴C△QDE=QE+QD+DE=QE+QD'+DE=ED'+DE= , 即点Q坐标(- , -), ∴△QDE的周长最小值为。
18. (1)(-2,1);(2,4) (2)解:∵OC平分∠ACB,
∴∠1=∠2,
∵AC∥y轴,
∴∠3=∠2,
∴∠1=∠3,
∴CD=DO.
作CE⊥y轴于点E,连接AB交y轴于点F,
∵点A,点B关于y轴对称,
∴BF⊥y轴,
∴∠CED=∠BFD,
∵B(-2,1),C(2,4),
∴CE=BF=2,
在△CDE和△BDF中,
DCED=DBFDDCDE=DBDF,CE=BF,
∴△CDE≌△BDF(AAS).
∴CD=BD,
∴BD=CD=OD,
∴∠DBO=∠DOB,
∵∠1+∠3+∠DBO+∠DOB=180°,
∴∠3+∠DOB=90°,
∴OB⊥OC
(3)解:连接BP,作PQ⊥x轴于点Q,
∵点A,点B关于y轴对称,
∴AB⊥y轴,
∴∠BAC=90°,
∵∠PAC=45°,
∴PA平分∠CAB,
∵OC平分∠ACB,
∴BP平分∠ABC.
∴∠BPC=135°,
∴∠BPO=45°.
∵∠BOP=90°,
∴OB=OP,
在△BOF和△POQ中,
DBFO=DPQO,DBOF=DPOQ,OB=OP,
∴△BOF≌△POQ(AAS).
∴PQ=BF=2,OQ=OF=1,
∴P(1,2).
19. (1)解:画图如图所示:
(2)解:由图可得,点A1的坐标是(1,﹣1),点B1的坐标是(﹣4,﹣1),点C1的坐标是(﹣3,1) (3)解:∵AB为公共边,
∴与△ABC全等的三角形的第三个顶点的坐标为(0,﹣3),(0,1)或(3,﹣3)
20. (1)证明:连接 BD .
∵AD=4m , AB=3m , ∠BAD=90°,
∴BD=5m .
又∵BC=12m , CD=13m ,
∴BD2+BC2=CD2 .
∴BD⊥CB
(2)解:四边形 ABCD 的面积=△ABD 的面积+△BCD 的面积
= ?×3×4+ ×12×5
=6+30
=36(m2).
故这块土地的面积是 36m2
(3)解:∵S△PBD= S 四边形ABCD
∴ ?PD?AB= ?×36, ∴ ?PD×3=9,
∴PD=6,
∵D(0,4),点 P 在 y 轴上,
∴P 的坐标为(0,-2)或(0,10).
21. (1)解:1﹣a=﹣3,a=4 (2)解:由a=4得:2a﹣12=2×4﹣12=﹣4,又点Q(x,y)位于第二象限,所以y>0;
取y=1,得点Q的坐标为(﹣4,1)
(3)解:因为点P(2a﹣12,1﹣a)位于第三象限,
所以 ,
解得:1<a<6.
因为点P的横、纵坐标都是整数,所以a=2或3或4或5;
当a=2时,1﹣a=﹣1,所以PQ>1;
当a=3时,1﹣a=﹣2,所以PQ>2;
当a=4时,1﹣a=﹣3,所以PQ>3;
当a=5时,1﹣a=﹣4,所以PQ>4.
22.【答案】(1)解:点B的坐标(3,2);
(2)解:长方形OABC周长=2×(2+3)=10,
∵长方形OABC的周长分成2:3的两部分,
∴两个部分的周长分别为4,6,
∵点C的坐标是(0,2),点D在边OA上,
∴OD=2,
∴点D的坐标为(2,0)
(3)解:如图所示,△CD′C′即为所求作的三角形,
CC′=3,点D′到CC′的距离为2,
所以,△CD′C′的面积= ×3×2=3
23. (1)4 (2)(0,2)或(0,-2) (3)90 (4)解:连接AD,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠EAO= ∠BAC, ∠EDO= ∠ODB,
∴∠EAO+∠EDO= (∠BAC+∠ODB=45°,
∵∠AED+∠EAD+∠EDA=180° , 即∠AED+∠EAO+∠OAD+∠EDO+∠ODA=180°,
∵∠OAD+∠ODA=90°,
∴∠AED+45°+90°=180°,
∴∠AED=45°.
24.(1)解:已知点A(0,2),B(3,0),C(3,4), 过A点作BC边上的高,交BC于点H, 则三角形ABC的面积为:S= BC?AH= ×4×3=6 (2)解:四边形ABOP的面积可以看作是△APO和△AOB的面积和, ∵P在第二象限,∴m<0,SAPOB=S△AOB+SAPO= + ×(﹣m)×2=3﹣m. 故四边形ABOP的面积为3﹣m (3)解:当四边形ABOP的面积与△ABC的面积相等时, 即3﹣m=6,得m=﹣3, 此时P点坐标为:(﹣3, ), 存在P点,使四边形ABOP的面积与△ABC的面积相等.
25.(1)北;西30°;400;南;西50°;600 (2)解:因为400米=40000厘米,
则中医院到邮电局的图上距离是:40000× =2(厘米);
如图所示,即为中医院的位置:
(3)24
26.(1)解:∵点A(﹣2,0),B(0,3), ∴OA=2,OB=3, ∴△AOB的面积= ×2×3=3 (2)解:由平移得,A′(2,0),B′(4,3), 当C在x轴上时,则S△A′B′C= A′C?3=9, ∴A′C=6, 设C(x,0),则有|x+2|=6, ∴x=﹣4,x=8, ∴C(﹣4,0)或(8,0); 当C在y轴的正半轴上时,设C(0,y),则S△A′B′C= ?[4(3+y)﹣2y﹣3×3]=9, 解得:y=6, 当C在y轴的负半轴上时,设C(0,y),则S△A′B′C= ?[4(3﹣y)+2y﹣3×3]=9, 解得:y=﹣12, ∴C(0,9)或(0,﹣12), 综上所述,C((﹣4,0)或(8,0)或(0,9)或(0,﹣12)
27.(1)梯 (2)解:∵A(﹣1,0),B(2+ ,0),C(2,1),D(0,1),
∴AB=3+ ,CD=2,
∴四边形ABCD的面积= (AB+CD)?OD= (3+ )×1= (3)解:A′(﹣1﹣ ,0),B′(2,0),C′(2﹣ ,1),D′(﹣ ,1)
28.(1)解:如图所示,△A1B1C1即为所求。 (2)解:A1(-4, -5),B1(﹣3,- 2),C1(4,1) (3)解:? 由图可得S△ABC=6×8×-1×3×-1×3-3×7×=9 又AC==10 ∵AC×h=S△ABC ∴h=9×2÷10=1.8 所以△ABC的AC边上的高为1.8
29. (1) (2)(2,-1);(-1,-3) (3)(4, 2)或(-4,-6)
30.(1)(2,2) (2)解:如图所示:△A1B1C1 , 即为所求 (3)(3,4) (4)解:△ABC的面积为:2×3﹣ ×2×2﹣ ×1×1﹣ ×1×3=2
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
