浙教版2019-2020八年级数学上册期末冲刺满分 专题一 全等三角形(30题含答案)
文档属性
| 名称 | 浙教版2019-2020八年级数学上册期末冲刺满分 专题一 全等三角形(30题含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-30 00:00:00 | ||
图片预览



文档简介
2019-2020浙教版八年级数学上册期末冲刺满分专题一全等三角形
1.如图,△ABC中,∠A=40°,
(1)若点P是∠ABC与∠ACB平分线的交点,求∠P的度数;
(2)若点P是∠CBD与∠BCE平分线的交点,求∠P的度数;
(3)若点P是∠ABC与∠ACF平分线的交点,求∠P的度数;
(4)若∠A=β,求(1)(2)(3)中∠P的度数(用含β的代数式表示,直接写出结果)
2.如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.
(1)当∠A=40°,∠ABC=60°时,求∠BPC的度数;
(2)当∠A=α°时,求∠BPC的度数.(用α的代数式表示)
(3)小明研究时发现:如果延长AB至D,再过点B作BQ⊥BP,那么BQ就是∠CBD的平分线。请你证明小明的结论.
3.???
(1)【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,在△ABC中,AD是△ABC的中线,若AB=10,AC=8,求AD的取值范围.
??
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
Ⅰ.由已知和作图能得到△ADC≌△EDB,依据是________.
A.SSS? B.SAS? C.AAS? D.ASA
Ⅱ.由“三角形的三边关系”可求得AD的取值范围是________.
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
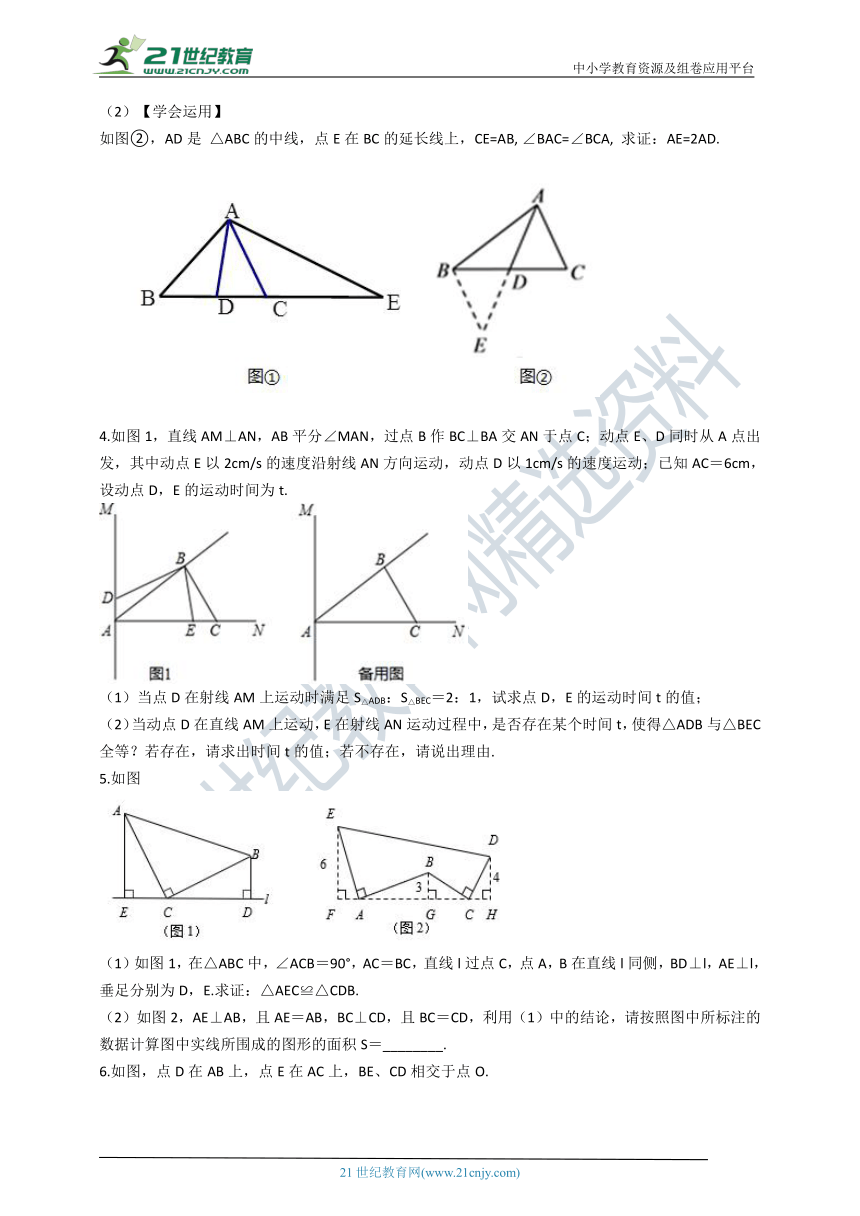
(2)【学会运用】
如图②,AD是 △ABC的中线,点E在BC的延长线上,CE=AB, ∠BAC=∠BCA, 求证:AE=2AD.
4.如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.
(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;
(2)当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
5.如图
(1)如图1,在△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A,B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D,E.求证:△AEC≌△CDB.
(2)如图2,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,利用(1)中的结论,请按照图中所标注的数据计算图中实线所围成的图形的面积S=________.
6.如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
7.如图1,线段AB、CD相交于点O,连结AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)仔细观察,在图2中“8字形”有多少个;
(3)图2中,当∠D=50°,∠B=40°时,求∠P的度数.
8.(1)已知:如图1,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点O,求证:∠BOC=90°+ ∠A;
(1)如图2,在△ABC中,BP,CP分别是△ABC的外角∠DBC和∠ECB的平分线,试探究∠BPC与∠A的关系.
(2)如图3,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究∠BEC与∠A的关系.
9.如图1,AB=12,AC⊥AB,BD⊥AB,AC=BD=8。点P在线段AB上以每秒2个单位的速度由点A向点B运动,同时,点Q在线段BD上由B点向点D运动。它们的运动时间为t(s).
???????
(1)若点Q的运动速度与点P的运动速度相等,当t=2时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变。设点Q的运动速度为每秒x个单位,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t的值;若不存在,请说明理由。
10.如图,已知△ABC中,AB=AC=12cm,∠B=∠C,BC=9cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm每秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动:
①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明理由;
②点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?
(2)若点Q以&的运动速度从点C出发点P以原来运动速度从点B同时出发,都逆时针沿△ABC的三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
11.在△ABC 中,AE、BF 是角平分线,交于 O 点.
(1)如图 1,AD 是高,∠BAC=90°,∠C=70°,求∠DAC 和∠BOA 的度数;
(2)如图 2,若 OE=OF,求∠C 的度数;
(3)如图 3,若∠C=90°,BC=8,AC=6,S△CEF=4,求 S△AOB.
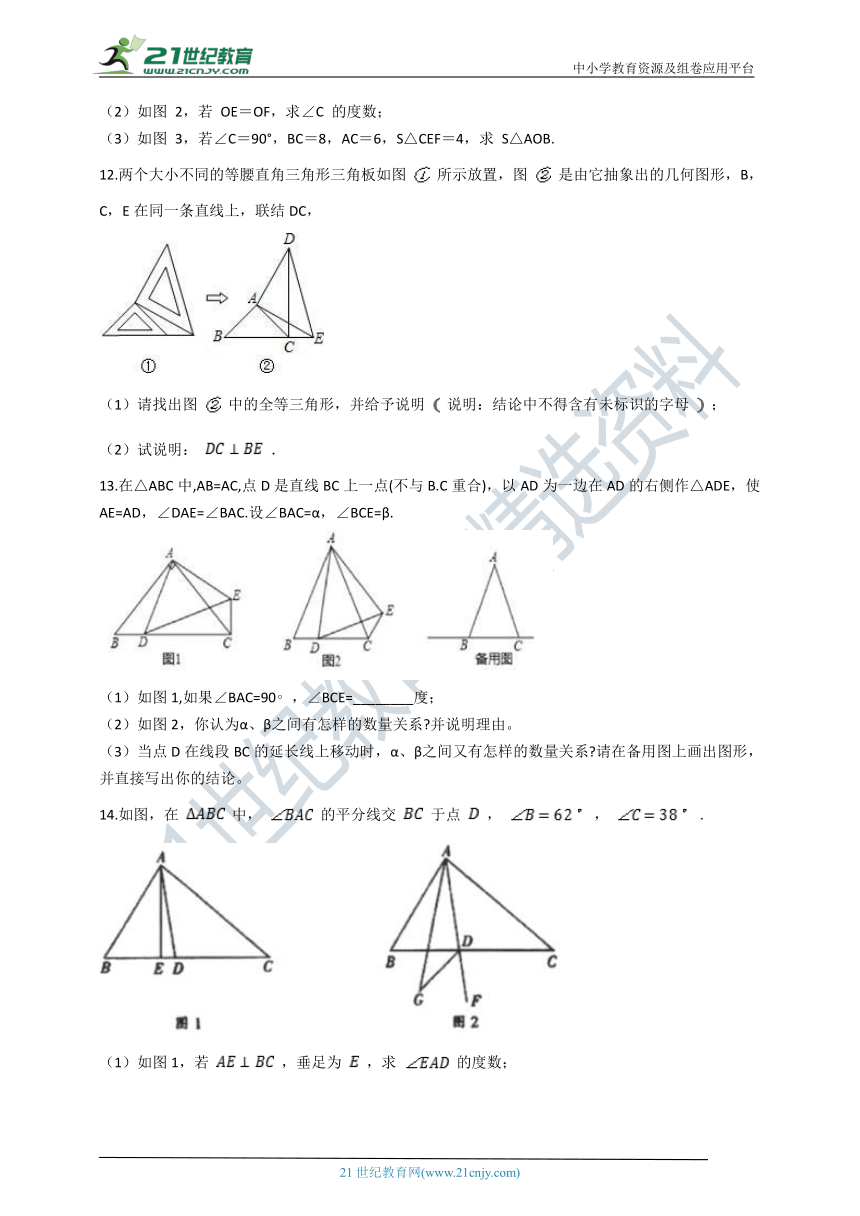
12.两个大小不同的等腰直角三角形三角板如图 所示放置,图 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
(1)请找出图 中的全等三角形,并给予说明 说明:结论中不得含有未标识的字母 ;
(2)试说明: .
13.在△ABC中,AB=AC,点D是直线BC上一点(不与B.C重合),以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC.设∠BAC=α,∠BCE=β.
(1)如图1,如果∠BAC=90°,∠BCE=________度;
(2)如图2,你认为α、β之间有怎样的数量关系?并说明理由。
(3)当点D在线段BC的延长线上移动时,α、β之间又有怎样的数量关系?请在备用图上画出图形,并直接写出你的结论。
14.如图,在 中, 的平分线交 于点 , , .
(1)如图1,若 ,垂足为 ,求 的度数;
(2)如图2,若点 是 延长线上的一点, 、 的平分线交于点 ,求 的度数.
15.如图,在△ABC中,AC
(1)已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.
(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q.连接AQ若∠AQC=3∠B,求∠B的度数.
16.如图,在 中, , 为 的中点, 分别为边 上的点,且 .
?
(1)求证: .
(2)当 时,求 的度数.
17.如图
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由.
18.如图,在△ABC中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD≌△ACE;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.
19.如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
20. 中,三个内角的平分线交于点O,过点O作 ,交边AB于点D.
(1)如图1, ①若∠ABC=40°,则∠AOC=________,∠ADO=________; ②猜想∠AOC与∠ADO的关系,并说明你的理由________。
(2)如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F . 若∠AOC=105°,∠F=32°,则∠AOD=________°.
21.△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E , 连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
22.如图:在△ABC中,己知∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M连接MD,过点D作DN⊥MD,交BM于点N.
(1)求证:△DBN≌△DCM;
(2)设CD与BM相交于点E,若点E是CD的中点,试探究线段NE、ME、CM之间的数量关系,并证明你的结论.
23.如图
(1)如图1,AD是△ABC的一条中线,求证:S△ABD=S△ACD;
(2)请运用第(1)题的结论解答下列问题:如图2,△ABC三边的中线AD,BE,CF交于一点G,若S△ABC=60,求图中阴影部分的面积.
24.如图:△ABC的边BC的高为AF,AC边上的高为BG,中线为AD,AF=6,BC=12,BG=5,
(1)求△ABD的面积.
(2)求AC的长.
(3)△ABD和△ACD的面积有何关系.
25.已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)试说明:BE=CF;
(2)若AF=3,BC=4,求△ABC的周长.
26.阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
(1)如图1,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是________;
(2)问题解决:
如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,边CD上的两点,且∠EAF= ∠BAD,求证:BE+DF=EF.
(3)问题拓展:
如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC外角平分线上一点,DE⊥AC交CA延长线于点E,F是AC上一点,且DF=DB.
求证:AC﹣AE= AF.
27.如图1所示,等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)求证:∠ABD=∠CAE;
(2)求证:DE=BD+CE;
(3)当直线MN运动到如图2所示位置时,其余条件不变,直接写出线段DE、BD、CE之间的数量关系.
28.问题情境:如图1,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)特例探究:如图2,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
(2)归纳证明:如图3,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)拓展应用:如图4,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为3,则△ACF与△BDE的面积之和为________.
29.如图1所示,AE=AF,AE⊥AF,E,F,B在同一直线上,AB=AC,∠BAC=90°.
(1)求证:∠EAB=∠FAC
(2)判断△AEB与△AFC是否全等?若全等,请给出证明;若不全等,说明理由
(3)当EF=FB时,如图2,求证:CE=CB.
30.已知△ABC和△CDE都为等腰直角三角形,∠ACB=∠ECD=90°.
(1)探究:如图①,当点A在边EC上,点C在线段BD上时,连结BE、AD.求证:BE=AD,BE⊥AD.
(2)拓展:如图②,当点A在边DE上时,AB、CE交于点F,连结BE.若AE=2,AD=4,则 的值为________.
答案
1. (1)解:∵∠A=40°,
∴∠ABC+∠ACB=140°,
∴∠PBC+∠PCB= (∠ABC+∠ACB)= ×140°=70°,
∴∠BPC=180°-70°=110°
(2)解:∵∠DBC=∠A+∠ACB,
∵P为△ABC两外角平分线的交点,
∴ ∠DBC= ∠A+ ∠ACB,
同理可得: ∠BCE= ∠A+ ∠ABC,
∵∠A+∠ACB+∠ABC=180°,
∴ (∠ACB+∠ABC)=90°- ∠A,
∵180°-∠BPC= ∠DBC+ ∠BCE= ∠A+ ∠ACB+ ∠A+ ∠ABC,
∴180°-∠BPC=∠A+ ∠ACB+ ∠ABC,180°-∠BPC=∠A+90°- ∠A,
∴∠BPC=90°- ∠A=70°
(3)解:∵点P是∠ABC与∠ACF平分线的交点
∴
∵∠PCF=∠P+∠PBC,∠ACF=∠A+∠ABC
∴2(∠P+∠PBC)=∠A+∠ABC
∴
(4)解:若 在(1)中 ;在(2)中,同理得 ;在(3)中同理可得∠P= β
2. (1)解: ∵∠ABC与∠ACB的平分线交于点P, ∴∠ABC=2∠2,∠ACB=2∠4, ∴∠ABC+∠ACB=2∠2+2∠4 ∵∠A=40°,∠ABC=60°, ∴∠ACB=2∠2=180°-40°-60°=80°, ∴∠2=30°,∠4=40°, ∴∠BPC=180°-∠2-∠4=180°-30°-40°=110°. (2)解: ∵∠ABC与∠ACB的平分线交于点P,
∴∠ABC=2∠2,∠ACB=2∠4, ∵∠A= α° , ∴∠ABC+∠ACB=180°-∠A=180°- α° 即2∠2+2∠4=180°- α° ∴∠2+∠4= , ∵∠BPC=180°-(∠2+∠4)=180°-()=;
(3)证明:如图,
∵BQ⊥BP ∴∠QBP=∠2+∠QBC=90°, ∴∠1+∠QBP+∠DBQ=180°, ∴∠1+∠DBQ=90°, ∵∠1=∠2 ∴∠QBC=∠DBQ, ∴BQ是∠CBD的平分线.
3. (1)SAS ;14. (1)解:如图2中,
①当E在线段AC上时,作BH⊥AC于H,BG⊥AM于G.
∵BA平分∠MAN,
∴BG=BH,
∵S△ADB:S△BEC=2:1,AD=t,AE=2t,
∴ ?t?BG: ?(6﹣2t)?BH=2:1,
∴t= s.
②当点E运动到AC延长线上,同法可得t=4时,也满足条件,
∴当t= s或4s时,满足S△ADB:S△BEC=2:1
(2)解:存在.当D在AM延长线上时
∵∠BAD=∠BCE=45°, ∴BA=BC,
∴当AD=EC时,△ADB≌△CEB,
∴t=6﹣2t,
∴t=2s,
∴t=2s时,△ADB≌△CEB.
当D在MA延长线上时,2t﹣6=t,t=6s,
综上所述,满足条件的t的值为2s或6s
5. (1)证明:如图1中,
∵BD⊥l,AE⊥l,
∴∠AEC=∠CDB=90°,
∴∠CAE+∠ACE=90°,
∴∠BCD+∠ACE=90°,
∴∠CAE=∠BCD,
在△AEC和△CDB中
,
∴△AEC≌△CDB(AAS)
(2)解:如图2中,因为AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,
由(1)可知:△EFA≌△AGB,△BGC≌△CHD,
∴EF=AG=6,AF=BG=CH=3,CG=DH=4,
∴S= (6+4)×16-18-12=50.
故答案为50.
6. (1)解:∵∠A=50°,∠C=30°,∴∠BDO=80°;∵∠BOD=70°,∴∠B=30° (2)解:∠BOC=∠A+∠B+∠C.
理由:∵∠BOC=∠BEC +∠C,∠BEC=∠A+∠B,
∴∠BOC=∠A+∠B+∠C
7. (1)解:∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B
(2)解:①线段AB、CD相交于点O,形成“8字形”;
②线段AN、CM相交于点O,形成“8字形”;
③线段AB、CP相交于点N,形成“8字形”;
④线段AB、CM相交于点O,形成“8字形”;
⑤线段AP、CD相交于点M,形成“8字形”;
⑥线段AN、CD相交于点O,形成“8字形”;
故“8字形”共有6个;
(3)解:∠DAP+∠D=∠P+∠DCP,①
∠PCB+∠B=∠PAB+∠P,②
∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②得:
∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,
即2∠P=∠D+∠B,
又∵∠D=50°,∠B=40°,
∴2∠P=50°+40°,
∴∠P=45°
8. (1)解:∠BPC=90°? ∠A.
证明:∵BP、CP为△ABC两外角∠ABC、∠ACB的平分线,∠A为x°,
∴∠BCP= (∠A+∠ABC)、∠PBC= (∠A+∠ACB),
由三角形内角和定理得,∠BPC=180°?∠BCP?∠PBC=180°? [∠A+(∠A+∠ABC+∠ACB)]=180°? (∠A+180°)=90°? ∠A
(2)2∠BEC=∠A.
证明:∵CE为∠ACB的角平分线,BE为△ABC外角∠ABD的平分线,两角平分线交于点E,
∴∠1=∠2,∠ABE= (∠A+2∠1),∠3=∠4,
在△ACF中,∠A=180°?∠1?∠3
∴∠1+∠3=180°?∠A①
在△BEF中,∠E=180°?∠4?∠ABE=180°?∠3? (∠A+2∠1),
即2∠E=360°?2∠3?∠A?2∠1=360°?2(∠1+∠3)?∠A②,
把①代入②得2∠E=∠A,即2∠BEC=∠A.
9. (1)解:△ACP与△BPQ全等,PC⊥PQ,理由如下: 当t=2时,AP=BQ=2×2=4,BP=AB-AP=12-4=8=AC, ∵ AC⊥AB,BD⊥AB,?∴∠PAB=∠PBQ=90°, 在Rt△PAC和Rt△QBP中, , ∴Rt△PAC≌Rt△QBP, ∴∠APC=∠PQB, ∵∠PQB+∠QPB=90°, ∴∠APC+∠QPB=90°, 即PC⊥PQ. (2)解:存在实数x,使得△ACP与△BPQ全等,理由如下: 1)若△ACP≌△BQP,则AC=BQ,AP=BP, 即,解得; 2)若△ACP≌△BPQ,则AC=BP,AP=BO, 即,解得.
10. (1)解:①∵t=1(秒),
∴BP=CQ=3(厘米)
∵AB=12,D为AB中点,
∴BD=6(厘米)
又∵PC=BC-BP=9-3=6(厘米)
∴PC=BD
在△BPD与△CQP中,
∴△BPD≌△CQP(SAS),
②∵VP≠VQ ,
∴BP≠CQ,
又∵∠B=∠C,
要使△BPD≌△CPQ,只能BP=CP=4.5,
∵△BPD≌△CPQ,
∴CQ=BD=6.
∴点P的运动时间t= = =1.5(秒),
此时VQ= = =4(厘米/秒)
(2)解:因为VQ>VP , 只能是点Q追上点P,即点Q比点P多走AB+AC的路程
设经过x秒后P与Q第一次相遇,依题意得4x=3x+2×12,
解得x=24(秒)
此时P运动了24×3=72(厘米)
又∵△ABC的周长为33厘米,72=33×2+6,
∴点P、Q在BC边上相遇,即经过了24秒,点P与点Q第一次在BC边上相遇.
11. (1)解:∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=180°-90°-70°=20°;
∵∠BAC=50°,∠C=70°,
∴∠BAO=25°,∠ABC=60°,
∵BF是∠ABC的角平分线,
∴∠ABO=30°,
∴∠BOA=180°-∠BAO-∠ABO=180°-25°-30°=125°
(2)解:如图2:连接OC,
∴AE、BF是角平分线,交于O点,
∴OC是∠ACB的角平分线,
∴∠OCF=∠OCE,
过O作OM⊥BC,ON⊥AC,
则OM=ON,
在Rt△OEM与Rt△OFN中,
?,
∴Rt△OEM≌Rt△OFN,(HL),
∴∠EOM=∠FON,
∴∠MON=∠EOF=180°-∠C,
∵AE、BF是角平分线,
∴∠AOB=90°+ ∠ACB,
即90°+ ∠ACB=180°-∠ACB,
∴∠ACB=60°
(3)解:∵∠C=90°,BC=8,AC=6,
∴AB= =10,
∵AE是角平分线,
∴ ,
∴BE=5,CE=3,
∵S△CEF= EC?CF= ×3?CF=4,
∴CF= ,
∴AF= ,
∵S△ABC= BC?AC= ×8×6=24,
∴S△ABF=S△ABC-S△BCF=24- ×8× =
∵AE平分∠BAC,
∴
∴ =3,
∴
∴S△AOB= =10.
12. (1)解:∵△ABC,△DAE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°.
∠BAE=∠DAC=90°+∠CAE,
在△BAE和△DAC中
∴△BAE≌△CAD(SAS)
(2)解:由(1)得△BAE≌△CAD.
∴∠DCA=∠B=45°.
∵∠BCA=45°,
∴∠BCD=∠BCA+∠DCA=90°,
∴DC⊥BE.
13. (1)90 (2)解:由(1)中可知β=180°?α,
∴α、β存在的数量关系为α+β=180°
(3)解:连接AD,作AE使得∠DAE=∠BAC,AE=AD,连接DE、CE,可得下图:
∵∠BAD=∠BAC+∠CAD,∠CAE=∠DAE+∠CAD,∴∠BAD=∠CAE;
在△ABD和△ACE中,
?
∴△ABD≌△ACE(SAS);
∴∠B=∠ACE;
∴∠BCE=∠BCA+∠ACE=∠BCA+∠B=180°?∠BAC.
∴α、β存在的数量关系为α+β=180°
14. (1)解:由(1)可得
? 的角平分线是AG
? ?
? ?
? ?
?DG是 的平分线
? ?
?
? ?
15. (1)证明:因为点P在AB的垂直平分线上,
所以PA=PB,
所以∠PAB=∠B,
所以∠APC=∠PAB+∠B=2∠B.
(2)解:根据题意,得BQ=BA,
所以∠BAQ=∠BQA,
设∠B=x,
所以∠AQC=∠B+∠BAQ=3x,
所以∠BAQ=∠BQA=2x,
在△ABQ中,x+2x+2x=180°.
解得x=36°,即∠B=36°
16. (1)证明:∵ ,
∴ .
∵ 为 的中点,
∴ .
又∵ ,
∴ .
(2)解:∵ ,
∴ .
∵ ,
∴ .
由 得 ,
∴
17. (1)解:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE
(2)解:∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
18. (1)证明:∵
∴
又∵
∴
在△ABD和△ACE中
∴△ABD≌△ACE;
(2)解: 理由如下:
连接FE, ∵
∴
由(1)知△ABD≌△ACE
∴ ,
∴
∴
∴ ?
∵AF平分
∴
在△DAF和△EAF中
∴△DAF≌△EAF
∴ .
∴ ;
(3)解:过点A作 于G
由(2)知 ?
∴
∴
∵
∴
∴ ?
∴在 中 .
19. (1)解:如图1,过点B作BC⊥x轴于点C,
∵△AOB为等边三角形,且OA=2,
∴∠A0B=60°,OB=OA=2,
∴∠BOC=30°,而∠OCB=90°,
∴BC= OB=1,OC= ,
∴点B的坐标为B( ,1)
(2)解:∠ABO=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ、AO=AB、∠PAQ=∠OAB,
∴∠PAO=∠QAB,
在△APO与△AQB中,
∴△APO=△AQB(SAS),
∴∠ABQ=∠AOP=90°
(3)解:当点P在x轴负半轴上时,点Q在点B的下方,
∵AB∥OQ,∠BQO=90°,∠BOQ=∠ABO=60°.
又OB=OA=2,可求得BQ= ,
由(2)可知,△APO≌△AQB,
∴OP=BQ= ,
∴此时P的坐标为(- ,0).
当点P在x轴正半轴时,点Q必在第一象限,OQ和AB不可能平行;
20. (1)110° ;110° ;相等,理由设∠ABC=α, ∴∠BAC+∠BCA=180°-α, ∵△ABC中,三个内角的平分线交于点O, ∴∠OAC+∠OCA=(∠BAC+∠BCA)=90°-α, ∴∠AOC=180°-(∠OAC+∠OCA)=90°+α, ∵OB平分∠ABC, ∴∠ABO=∠ABC=α, ∵OD⊥OB, ∴∠BOD=90°, ∴∠BDO=90°-α, ∴∠ADO=180°-∠BOD=90°+α, ∴∠AOC=∠ADO (2)43
21. (1)解:设AP=x,则BQ=x,
∵∠BQD=30°,∠C=60°,
∴∠QPC=90°,
∴QC=2PC,即x+6=2(6-x),
解得x=2,
即AP=2
(2)证明:如图,
过P点作PF∥BC,交AB于F,
∵PF∥BC,
∴∠PFA=∠FPA=∠A=60°,
∴PF=AP=AF,
∴PF=BQ,
又∵∠BDQ=∠PDF,∠DBQ=∠DFP,
∴△DQB≌△DPF,
∴DQ=DP即D为PQ中点
(3)解:运动过程中线段ED的长不发生变化,是定值为3,
理由:∵PF=AP=AF,PE⊥AF,
∴EF= AF ,
又∵△DQB≌△DPF,
∴DF=DB , 即DF= BF ,
∴ED=EF+DF= (AF+BF)= AB=3
22. (1)证明: ∵∠ABC=45°,CD⊥AB, ∴∠ABC=∠DCB=45°, ∴BD=DC, ∵∠BDC=∠MDN=90°, 即∠BDN+∠NDE=∠MDC+∠NDE=90°, ∴∠BDN=∠CDM, ∵CD⊥AB,BM⊥AC, ∴∠ABM=90°﹣∠A=∠ACD, 在△DBN和△DCM中,
, ∴△DBN≌△DCM(ASA).
(2)结论:NE﹣ME=CM,理由如下:
证明:由(1)可知△DBN≌△DCM, ∴DM=DN,
作DF⊥MN于点F,又 ND⊥MD, ∴DF=FN, ∵E为CD中点, ∴CE=DE, 在△DEF和△CEM中,
,
∴△DEF≌△CEM(AAS), ∴EF = EM,DF = CM, ∴CM=DF=FN=NE﹣FE=NE﹣ME.
23. (1)解:如图1,过点A作AM⊥BC,
∵AD是△ABC的中线,
∴BD=CD= BC,
∵S△ABD= BD×AM,S△ACD= CD×AM
∴S△ABD=S△ACD;
(2)解:∵△ABC的三条中线AD,BE,CF交于点G,
∴S△CGE=S△AGE=S△BGF=S△BGD=S△BDG=S△CDG ,
∵S△ABC=60
∴S△CGE=S△BGF= ×60=10,
∴S阴影=S△CGE+S△BGF=20.
24. (1)解:∵△ABC的边BC上的高为AF,AF=6,BC=12,
∴△ABC的面积= BC?AF= ×12×6=36
(2)解:∵AC边上的高为BG,BG=5,
∴△ABC的面积= AC?BG=36,
∴AC=
(3)解:△ABD和△ACD的面积相等.
∵△ABC的中线为AD,
∴BD=CD,
∵△ABD以BD为底,△ACD以CD为底,而且等高,
∴S△ABD=S△ACD .
25. (1)解:连接DB、DC,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵DG垂直平分BC,
∴DB=DC,
在Rt△BED和Rt△CFD中,
DE=DF,BD=CD,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF
(2)解:∵∠DAE=∠DAF,∠AED=∠AFD=90°,AD=AD,
∴△AED≌△AFD,
∴AF=AE=3,
由(1)得:BE=CF,
∴△ABC的周长=AB+AC+BC=AE+EB+AF﹣CF+BC=AE+AF+BC=3+3+4=10.
26. (1)2<AD<10 (2)证明:延长CB到G,使BG=DF,
∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,
∴∠ADC=∠ABG,
在△ABG和△ADF中,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠GAB=∠FAD,
∵∠EAF= ∠BAD,
∴∠FAD+∠BAE=∠GAB+∠BAE= ∠BAD,
∴∠GAE=∠FAE,
在△AEG和△AEF中,
,
∴△AEG≌△AEF(SAS),
∴EF=GE,
∴EF=BE+BG=BE+DF
(3)证明:作DH⊥AB于H,在AB上截取BR=AF,
∵∠CAB=60°,∠ACB=90°,
∴∠ABC=30°,
∴AB=2AC,
∵点D是△ABC外角平分线上一点,DE⊥AC,DH⊥AB,
∴DE=DH,AH=AE,
在Rt△DEF和Rt△DHB中,
∴Rt△DEF≌Rt△DHB(HL)
∴∠DFA=∠DBA,
在△DAF和△DRB中,
,
∴△DAF≌△DRB(SAS)
∴DA=DR,
∴AH=HR=AE= AR,
∵AF=BR=AB﹣AR=2AC﹣2AE
∴AC﹣AE= AF.
27. (1)证明:∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
∴∠BAD+∠ABD=90°,
又∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE
(2)证明:在△BAD和△ACE中
∵ ,
∴△BAD≌△ACE(AAS),
∴BD=AE,AD=CE,
又DE=AE+AD,
∴DE=BD+CE
(3)解:DE=CE﹣BD,
同(2)可得△BAD≌△ACE,
故BD=AE,AD=CE,
又DE=AD﹣AE,
∴DE=CE﹣BD
28. (1)证明:如图②,∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠ABD+∠CAF=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
∴△ABD≌△CAF(AAS)
(2)证明:如图③,
∵∠1=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,
∴∠ABE=∠CAF,
∵∠2=∠FCA+∠CAF,∠BAC=∠BAE+∠CAF,∠2=∠BAC,
∴∠BAE=∠FCA,
在△ABE和△CAF中, ,
∴△ABE≌△CAF(ASA)
(3)1
29. (1)证明:∵AE⊥AF,∠BAC=90°,
∴∠EAB=∠FAC
(2)解:△AEB与△AFC全等.
理由如下:在△EAB和△FAC中,
,
∴△EAB≌△FAC
(3)证明:由(2)得,△EAB≌△FAC,
∴∠ACF=∠ABE,
∵∠ACF+∠AHC=90°,∠AHC=∠FHB,
∴∠FHB+∠ABE=90°
∴CF⊥BE,又EF=FB,
∴CE=CB.
30. (1)解:探究:延长DA交BE于F.
∵△ABC和△CDE都为等腰直角三角形,∠ACB=∠ECD=90°.
∴BC=CA,EC=CD,
∴△BCE≌△ACD,
∴BE=AD,∠BEC=∠ADC,
∵∠ACB=90°,
∴∠BEC+∠EBC=90°,
∴∠ADC+∠EBC=90°,
∴∠BFD=90°,
∴BE⊥AD
(2)解:拓展:作FM⊥DE于M,FN⊥BE于N.
由探究可知:BE⊥DE,BE=AD=4,∠FEM=∠FEB=45°,
∵FM⊥DE于M,FN⊥BE于N.
∴FM=FN,
∵ EB?FN+ ?AE?FM= BE?AE,
∴FM=FN= ,
∴EF= ,
∵CE=CD=3 ,
∴CF= ,
∴EF:CF=4:5.
故答案为 .
1.如图,△ABC中,∠A=40°,
(1)若点P是∠ABC与∠ACB平分线的交点,求∠P的度数;
(2)若点P是∠CBD与∠BCE平分线的交点,求∠P的度数;
(3)若点P是∠ABC与∠ACF平分线的交点,求∠P的度数;
(4)若∠A=β,求(1)(2)(3)中∠P的度数(用含β的代数式表示,直接写出结果)
2.如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.
(1)当∠A=40°,∠ABC=60°时,求∠BPC的度数;
(2)当∠A=α°时,求∠BPC的度数.(用α的代数式表示)
(3)小明研究时发现:如果延长AB至D,再过点B作BQ⊥BP,那么BQ就是∠CBD的平分线。请你证明小明的结论.
3.???
(1)【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,在△ABC中,AD是△ABC的中线,若AB=10,AC=8,求AD的取值范围.
??
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
Ⅰ.由已知和作图能得到△ADC≌△EDB,依据是________.
A.SSS? B.SAS? C.AAS? D.ASA
Ⅱ.由“三角形的三边关系”可求得AD的取值范围是________.
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(2)【学会运用】
如图②,AD是 △ABC的中线,点E在BC的延长线上,CE=AB, ∠BAC=∠BCA, 求证:AE=2AD.
4.如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.
(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;
(2)当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
5.如图
(1)如图1,在△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A,B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D,E.求证:△AEC≌△CDB.
(2)如图2,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,利用(1)中的结论,请按照图中所标注的数据计算图中实线所围成的图形的面积S=________.
6.如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
7.如图1,线段AB、CD相交于点O,连结AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)仔细观察,在图2中“8字形”有多少个;
(3)图2中,当∠D=50°,∠B=40°时,求∠P的度数.
8.(1)已知:如图1,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点O,求证:∠BOC=90°+ ∠A;
(1)如图2,在△ABC中,BP,CP分别是△ABC的外角∠DBC和∠ECB的平分线,试探究∠BPC与∠A的关系.
(2)如图3,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究∠BEC与∠A的关系.
9.如图1,AB=12,AC⊥AB,BD⊥AB,AC=BD=8。点P在线段AB上以每秒2个单位的速度由点A向点B运动,同时,点Q在线段BD上由B点向点D运动。它们的运动时间为t(s).
???????
(1)若点Q的运动速度与点P的运动速度相等,当t=2时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变。设点Q的运动速度为每秒x个单位,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t的值;若不存在,请说明理由。
10.如图,已知△ABC中,AB=AC=12cm,∠B=∠C,BC=9cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm每秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动:
①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明理由;
②点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?
(2)若点Q以&的运动速度从点C出发点P以原来运动速度从点B同时出发,都逆时针沿△ABC的三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
11.在△ABC 中,AE、BF 是角平分线,交于 O 点.
(1)如图 1,AD 是高,∠BAC=90°,∠C=70°,求∠DAC 和∠BOA 的度数;
(2)如图 2,若 OE=OF,求∠C 的度数;
(3)如图 3,若∠C=90°,BC=8,AC=6,S△CEF=4,求 S△AOB.
12.两个大小不同的等腰直角三角形三角板如图 所示放置,图 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
(1)请找出图 中的全等三角形,并给予说明 说明:结论中不得含有未标识的字母 ;
(2)试说明: .
13.在△ABC中,AB=AC,点D是直线BC上一点(不与B.C重合),以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC.设∠BAC=α,∠BCE=β.
(1)如图1,如果∠BAC=90°,∠BCE=________度;
(2)如图2,你认为α、β之间有怎样的数量关系?并说明理由。
(3)当点D在线段BC的延长线上移动时,α、β之间又有怎样的数量关系?请在备用图上画出图形,并直接写出你的结论。
14.如图,在 中, 的平分线交 于点 , , .
(1)如图1,若 ,垂足为 ,求 的度数;
(2)如图2,若点 是 延长线上的一点, 、 的平分线交于点 ,求 的度数.
15.如图,在△ABC中,AC
(1)已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.
(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q.连接AQ若∠AQC=3∠B,求∠B的度数.
16.如图,在 中, , 为 的中点, 分别为边 上的点,且 .
?
(1)求证: .
(2)当 时,求 的度数.
17.如图
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由.
18.如图,在△ABC中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD≌△ACE;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.
19.如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
20. 中,三个内角的平分线交于点O,过点O作 ,交边AB于点D.
(1)如图1, ①若∠ABC=40°,则∠AOC=________,∠ADO=________; ②猜想∠AOC与∠ADO的关系,并说明你的理由________。
(2)如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F . 若∠AOC=105°,∠F=32°,则∠AOD=________°.
21.△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E , 连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
22.如图:在△ABC中,己知∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M连接MD,过点D作DN⊥MD,交BM于点N.
(1)求证:△DBN≌△DCM;
(2)设CD与BM相交于点E,若点E是CD的中点,试探究线段NE、ME、CM之间的数量关系,并证明你的结论.
23.如图
(1)如图1,AD是△ABC的一条中线,求证:S△ABD=S△ACD;
(2)请运用第(1)题的结论解答下列问题:如图2,△ABC三边的中线AD,BE,CF交于一点G,若S△ABC=60,求图中阴影部分的面积.
24.如图:△ABC的边BC的高为AF,AC边上的高为BG,中线为AD,AF=6,BC=12,BG=5,
(1)求△ABD的面积.
(2)求AC的长.
(3)△ABD和△ACD的面积有何关系.
25.已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)试说明:BE=CF;
(2)若AF=3,BC=4,求△ABC的周长.
26.阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
(1)如图1,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是________;
(2)问题解决:
如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,边CD上的两点,且∠EAF= ∠BAD,求证:BE+DF=EF.
(3)问题拓展:
如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC外角平分线上一点,DE⊥AC交CA延长线于点E,F是AC上一点,且DF=DB.
求证:AC﹣AE= AF.
27.如图1所示,等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)求证:∠ABD=∠CAE;
(2)求证:DE=BD+CE;
(3)当直线MN运动到如图2所示位置时,其余条件不变,直接写出线段DE、BD、CE之间的数量关系.
28.问题情境:如图1,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)特例探究:如图2,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
(2)归纳证明:如图3,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)拓展应用:如图4,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为3,则△ACF与△BDE的面积之和为________.
29.如图1所示,AE=AF,AE⊥AF,E,F,B在同一直线上,AB=AC,∠BAC=90°.
(1)求证:∠EAB=∠FAC
(2)判断△AEB与△AFC是否全等?若全等,请给出证明;若不全等,说明理由
(3)当EF=FB时,如图2,求证:CE=CB.
30.已知△ABC和△CDE都为等腰直角三角形,∠ACB=∠ECD=90°.
(1)探究:如图①,当点A在边EC上,点C在线段BD上时,连结BE、AD.求证:BE=AD,BE⊥AD.
(2)拓展:如图②,当点A在边DE上时,AB、CE交于点F,连结BE.若AE=2,AD=4,则 的值为________.
答案
1. (1)解:∵∠A=40°,
∴∠ABC+∠ACB=140°,
∴∠PBC+∠PCB= (∠ABC+∠ACB)= ×140°=70°,
∴∠BPC=180°-70°=110°
(2)解:∵∠DBC=∠A+∠ACB,
∵P为△ABC两外角平分线的交点,
∴ ∠DBC= ∠A+ ∠ACB,
同理可得: ∠BCE= ∠A+ ∠ABC,
∵∠A+∠ACB+∠ABC=180°,
∴ (∠ACB+∠ABC)=90°- ∠A,
∵180°-∠BPC= ∠DBC+ ∠BCE= ∠A+ ∠ACB+ ∠A+ ∠ABC,
∴180°-∠BPC=∠A+ ∠ACB+ ∠ABC,180°-∠BPC=∠A+90°- ∠A,
∴∠BPC=90°- ∠A=70°
(3)解:∵点P是∠ABC与∠ACF平分线的交点
∴
∵∠PCF=∠P+∠PBC,∠ACF=∠A+∠ABC
∴2(∠P+∠PBC)=∠A+∠ABC
∴
(4)解:若 在(1)中 ;在(2)中,同理得 ;在(3)中同理可得∠P= β
2. (1)解: ∵∠ABC与∠ACB的平分线交于点P, ∴∠ABC=2∠2,∠ACB=2∠4, ∴∠ABC+∠ACB=2∠2+2∠4 ∵∠A=40°,∠ABC=60°, ∴∠ACB=2∠2=180°-40°-60°=80°, ∴∠2=30°,∠4=40°, ∴∠BPC=180°-∠2-∠4=180°-30°-40°=110°. (2)解: ∵∠ABC与∠ACB的平分线交于点P,
∴∠ABC=2∠2,∠ACB=2∠4, ∵∠A= α° , ∴∠ABC+∠ACB=180°-∠A=180°- α° 即2∠2+2∠4=180°- α° ∴∠2+∠4= , ∵∠BPC=180°-(∠2+∠4)=180°-()=;
(3)证明:如图,
∵BQ⊥BP ∴∠QBP=∠2+∠QBC=90°, ∴∠1+∠QBP+∠DBQ=180°, ∴∠1+∠DBQ=90°, ∵∠1=∠2 ∴∠QBC=∠DBQ, ∴BQ是∠CBD的平分线.
3. (1)SAS ;1
①当E在线段AC上时,作BH⊥AC于H,BG⊥AM于G.
∵BA平分∠MAN,
∴BG=BH,
∵S△ADB:S△BEC=2:1,AD=t,AE=2t,
∴ ?t?BG: ?(6﹣2t)?BH=2:1,
∴t= s.
②当点E运动到AC延长线上,同法可得t=4时,也满足条件,
∴当t= s或4s时,满足S△ADB:S△BEC=2:1
(2)解:存在.当D在AM延长线上时
∵∠BAD=∠BCE=45°, ∴BA=BC,
∴当AD=EC时,△ADB≌△CEB,
∴t=6﹣2t,
∴t=2s,
∴t=2s时,△ADB≌△CEB.
当D在MA延长线上时,2t﹣6=t,t=6s,
综上所述,满足条件的t的值为2s或6s
5. (1)证明:如图1中,
∵BD⊥l,AE⊥l,
∴∠AEC=∠CDB=90°,
∴∠CAE+∠ACE=90°,
∴∠BCD+∠ACE=90°,
∴∠CAE=∠BCD,
在△AEC和△CDB中
,
∴△AEC≌△CDB(AAS)
(2)解:如图2中,因为AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,
由(1)可知:△EFA≌△AGB,△BGC≌△CHD,
∴EF=AG=6,AF=BG=CH=3,CG=DH=4,
∴S= (6+4)×16-18-12=50.
故答案为50.
6. (1)解:∵∠A=50°,∠C=30°,∴∠BDO=80°;∵∠BOD=70°,∴∠B=30° (2)解:∠BOC=∠A+∠B+∠C.
理由:∵∠BOC=∠BEC +∠C,∠BEC=∠A+∠B,
∴∠BOC=∠A+∠B+∠C
7. (1)解:∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B
(2)解:①线段AB、CD相交于点O,形成“8字形”;
②线段AN、CM相交于点O,形成“8字形”;
③线段AB、CP相交于点N,形成“8字形”;
④线段AB、CM相交于点O,形成“8字形”;
⑤线段AP、CD相交于点M,形成“8字形”;
⑥线段AN、CD相交于点O,形成“8字形”;
故“8字形”共有6个;
(3)解:∠DAP+∠D=∠P+∠DCP,①
∠PCB+∠B=∠PAB+∠P,②
∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②得:
∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,
即2∠P=∠D+∠B,
又∵∠D=50°,∠B=40°,
∴2∠P=50°+40°,
∴∠P=45°
8. (1)解:∠BPC=90°? ∠A.
证明:∵BP、CP为△ABC两外角∠ABC、∠ACB的平分线,∠A为x°,
∴∠BCP= (∠A+∠ABC)、∠PBC= (∠A+∠ACB),
由三角形内角和定理得,∠BPC=180°?∠BCP?∠PBC=180°? [∠A+(∠A+∠ABC+∠ACB)]=180°? (∠A+180°)=90°? ∠A
(2)2∠BEC=∠A.
证明:∵CE为∠ACB的角平分线,BE为△ABC外角∠ABD的平分线,两角平分线交于点E,
∴∠1=∠2,∠ABE= (∠A+2∠1),∠3=∠4,
在△ACF中,∠A=180°?∠1?∠3
∴∠1+∠3=180°?∠A①
在△BEF中,∠E=180°?∠4?∠ABE=180°?∠3? (∠A+2∠1),
即2∠E=360°?2∠3?∠A?2∠1=360°?2(∠1+∠3)?∠A②,
把①代入②得2∠E=∠A,即2∠BEC=∠A.
9. (1)解:△ACP与△BPQ全等,PC⊥PQ,理由如下: 当t=2时,AP=BQ=2×2=4,BP=AB-AP=12-4=8=AC, ∵ AC⊥AB,BD⊥AB,?∴∠PAB=∠PBQ=90°, 在Rt△PAC和Rt△QBP中, , ∴Rt△PAC≌Rt△QBP, ∴∠APC=∠PQB, ∵∠PQB+∠QPB=90°, ∴∠APC+∠QPB=90°, 即PC⊥PQ. (2)解:存在实数x,使得△ACP与△BPQ全等,理由如下: 1)若△ACP≌△BQP,则AC=BQ,AP=BP, 即,解得; 2)若△ACP≌△BPQ,则AC=BP,AP=BO, 即,解得.
10. (1)解:①∵t=1(秒),
∴BP=CQ=3(厘米)
∵AB=12,D为AB中点,
∴BD=6(厘米)
又∵PC=BC-BP=9-3=6(厘米)
∴PC=BD
在△BPD与△CQP中,
∴△BPD≌△CQP(SAS),
②∵VP≠VQ ,
∴BP≠CQ,
又∵∠B=∠C,
要使△BPD≌△CPQ,只能BP=CP=4.5,
∵△BPD≌△CPQ,
∴CQ=BD=6.
∴点P的运动时间t= = =1.5(秒),
此时VQ= = =4(厘米/秒)
(2)解:因为VQ>VP , 只能是点Q追上点P,即点Q比点P多走AB+AC的路程
设经过x秒后P与Q第一次相遇,依题意得4x=3x+2×12,
解得x=24(秒)
此时P运动了24×3=72(厘米)
又∵△ABC的周长为33厘米,72=33×2+6,
∴点P、Q在BC边上相遇,即经过了24秒,点P与点Q第一次在BC边上相遇.
11. (1)解:∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=180°-90°-70°=20°;
∵∠BAC=50°,∠C=70°,
∴∠BAO=25°,∠ABC=60°,
∵BF是∠ABC的角平分线,
∴∠ABO=30°,
∴∠BOA=180°-∠BAO-∠ABO=180°-25°-30°=125°
(2)解:如图2:连接OC,
∴AE、BF是角平分线,交于O点,
∴OC是∠ACB的角平分线,
∴∠OCF=∠OCE,
过O作OM⊥BC,ON⊥AC,
则OM=ON,
在Rt△OEM与Rt△OFN中,
?,
∴Rt△OEM≌Rt△OFN,(HL),
∴∠EOM=∠FON,
∴∠MON=∠EOF=180°-∠C,
∵AE、BF是角平分线,
∴∠AOB=90°+ ∠ACB,
即90°+ ∠ACB=180°-∠ACB,
∴∠ACB=60°
(3)解:∵∠C=90°,BC=8,AC=6,
∴AB= =10,
∵AE是角平分线,
∴ ,
∴BE=5,CE=3,
∵S△CEF= EC?CF= ×3?CF=4,
∴CF= ,
∴AF= ,
∵S△ABC= BC?AC= ×8×6=24,
∴S△ABF=S△ABC-S△BCF=24- ×8× =
∵AE平分∠BAC,
∴
∴ =3,
∴
∴S△AOB= =10.
12. (1)解:∵△ABC,△DAE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°.
∠BAE=∠DAC=90°+∠CAE,
在△BAE和△DAC中
∴△BAE≌△CAD(SAS)
(2)解:由(1)得△BAE≌△CAD.
∴∠DCA=∠B=45°.
∵∠BCA=45°,
∴∠BCD=∠BCA+∠DCA=90°,
∴DC⊥BE.
13. (1)90 (2)解:由(1)中可知β=180°?α,
∴α、β存在的数量关系为α+β=180°
(3)解:连接AD,作AE使得∠DAE=∠BAC,AE=AD,连接DE、CE,可得下图:
∵∠BAD=∠BAC+∠CAD,∠CAE=∠DAE+∠CAD,∴∠BAD=∠CAE;
在△ABD和△ACE中,
?
∴△ABD≌△ACE(SAS);
∴∠B=∠ACE;
∴∠BCE=∠BCA+∠ACE=∠BCA+∠B=180°?∠BAC.
∴α、β存在的数量关系为α+β=180°
14. (1)解:由(1)可得
? 的角平分线是AG
? ?
? ?
? ?
?DG是 的平分线
? ?
?
? ?
15. (1)证明:因为点P在AB的垂直平分线上,
所以PA=PB,
所以∠PAB=∠B,
所以∠APC=∠PAB+∠B=2∠B.
(2)解:根据题意,得BQ=BA,
所以∠BAQ=∠BQA,
设∠B=x,
所以∠AQC=∠B+∠BAQ=3x,
所以∠BAQ=∠BQA=2x,
在△ABQ中,x+2x+2x=180°.
解得x=36°,即∠B=36°
16. (1)证明:∵ ,
∴ .
∵ 为 的中点,
∴ .
又∵ ,
∴ .
(2)解:∵ ,
∴ .
∵ ,
∴ .
由 得 ,
∴
17. (1)解:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE
(2)解:∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
18. (1)证明:∵
∴
又∵
∴
在△ABD和△ACE中
∴△ABD≌△ACE;
(2)解: 理由如下:
连接FE, ∵
∴
由(1)知△ABD≌△ACE
∴ ,
∴
∴
∴ ?
∵AF平分
∴
在△DAF和△EAF中
∴△DAF≌△EAF
∴ .
∴ ;
(3)解:过点A作 于G
由(2)知 ?
∴
∴
∵
∴
∴ ?
∴在 中 .
19. (1)解:如图1,过点B作BC⊥x轴于点C,
∵△AOB为等边三角形,且OA=2,
∴∠A0B=60°,OB=OA=2,
∴∠BOC=30°,而∠OCB=90°,
∴BC= OB=1,OC= ,
∴点B的坐标为B( ,1)
(2)解:∠ABO=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ、AO=AB、∠PAQ=∠OAB,
∴∠PAO=∠QAB,
在△APO与△AQB中,
∴△APO=△AQB(SAS),
∴∠ABQ=∠AOP=90°
(3)解:当点P在x轴负半轴上时,点Q在点B的下方,
∵AB∥OQ,∠BQO=90°,∠BOQ=∠ABO=60°.
又OB=OA=2,可求得BQ= ,
由(2)可知,△APO≌△AQB,
∴OP=BQ= ,
∴此时P的坐标为(- ,0).
当点P在x轴正半轴时,点Q必在第一象限,OQ和AB不可能平行;
20. (1)110° ;110° ;相等,理由设∠ABC=α, ∴∠BAC+∠BCA=180°-α, ∵△ABC中,三个内角的平分线交于点O, ∴∠OAC+∠OCA=(∠BAC+∠BCA)=90°-α, ∴∠AOC=180°-(∠OAC+∠OCA)=90°+α, ∵OB平分∠ABC, ∴∠ABO=∠ABC=α, ∵OD⊥OB, ∴∠BOD=90°, ∴∠BDO=90°-α, ∴∠ADO=180°-∠BOD=90°+α, ∴∠AOC=∠ADO (2)43
21. (1)解:设AP=x,则BQ=x,
∵∠BQD=30°,∠C=60°,
∴∠QPC=90°,
∴QC=2PC,即x+6=2(6-x),
解得x=2,
即AP=2
(2)证明:如图,
过P点作PF∥BC,交AB于F,
∵PF∥BC,
∴∠PFA=∠FPA=∠A=60°,
∴PF=AP=AF,
∴PF=BQ,
又∵∠BDQ=∠PDF,∠DBQ=∠DFP,
∴△DQB≌△DPF,
∴DQ=DP即D为PQ中点
(3)解:运动过程中线段ED的长不发生变化,是定值为3,
理由:∵PF=AP=AF,PE⊥AF,
∴EF= AF ,
又∵△DQB≌△DPF,
∴DF=DB , 即DF= BF ,
∴ED=EF+DF= (AF+BF)= AB=3
22. (1)证明: ∵∠ABC=45°,CD⊥AB, ∴∠ABC=∠DCB=45°, ∴BD=DC, ∵∠BDC=∠MDN=90°, 即∠BDN+∠NDE=∠MDC+∠NDE=90°, ∴∠BDN=∠CDM, ∵CD⊥AB,BM⊥AC, ∴∠ABM=90°﹣∠A=∠ACD, 在△DBN和△DCM中,
, ∴△DBN≌△DCM(ASA).
(2)结论:NE﹣ME=CM,理由如下:
证明:由(1)可知△DBN≌△DCM, ∴DM=DN,
作DF⊥MN于点F,又 ND⊥MD, ∴DF=FN, ∵E为CD中点, ∴CE=DE, 在△DEF和△CEM中,
,
∴△DEF≌△CEM(AAS), ∴EF = EM,DF = CM, ∴CM=DF=FN=NE﹣FE=NE﹣ME.
23. (1)解:如图1,过点A作AM⊥BC,
∵AD是△ABC的中线,
∴BD=CD= BC,
∵S△ABD= BD×AM,S△ACD= CD×AM
∴S△ABD=S△ACD;
(2)解:∵△ABC的三条中线AD,BE,CF交于点G,
∴S△CGE=S△AGE=S△BGF=S△BGD=S△BDG=S△CDG ,
∵S△ABC=60
∴S△CGE=S△BGF= ×60=10,
∴S阴影=S△CGE+S△BGF=20.
24. (1)解:∵△ABC的边BC上的高为AF,AF=6,BC=12,
∴△ABC的面积= BC?AF= ×12×6=36
(2)解:∵AC边上的高为BG,BG=5,
∴△ABC的面积= AC?BG=36,
∴AC=
(3)解:△ABD和△ACD的面积相等.
∵△ABC的中线为AD,
∴BD=CD,
∵△ABD以BD为底,△ACD以CD为底,而且等高,
∴S△ABD=S△ACD .
25. (1)解:连接DB、DC,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵DG垂直平分BC,
∴DB=DC,
在Rt△BED和Rt△CFD中,
DE=DF,BD=CD,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF
(2)解:∵∠DAE=∠DAF,∠AED=∠AFD=90°,AD=AD,
∴△AED≌△AFD,
∴AF=AE=3,
由(1)得:BE=CF,
∴△ABC的周长=AB+AC+BC=AE+EB+AF﹣CF+BC=AE+AF+BC=3+3+4=10.
26. (1)2<AD<10 (2)证明:延长CB到G,使BG=DF,
∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,
∴∠ADC=∠ABG,
在△ABG和△ADF中,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠GAB=∠FAD,
∵∠EAF= ∠BAD,
∴∠FAD+∠BAE=∠GAB+∠BAE= ∠BAD,
∴∠GAE=∠FAE,
在△AEG和△AEF中,
,
∴△AEG≌△AEF(SAS),
∴EF=GE,
∴EF=BE+BG=BE+DF
(3)证明:作DH⊥AB于H,在AB上截取BR=AF,
∵∠CAB=60°,∠ACB=90°,
∴∠ABC=30°,
∴AB=2AC,
∵点D是△ABC外角平分线上一点,DE⊥AC,DH⊥AB,
∴DE=DH,AH=AE,
在Rt△DEF和Rt△DHB中,
∴Rt△DEF≌Rt△DHB(HL)
∴∠DFA=∠DBA,
在△DAF和△DRB中,
,
∴△DAF≌△DRB(SAS)
∴DA=DR,
∴AH=HR=AE= AR,
∵AF=BR=AB﹣AR=2AC﹣2AE
∴AC﹣AE= AF.
27. (1)证明:∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
∴∠BAD+∠ABD=90°,
又∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE
(2)证明:在△BAD和△ACE中
∵ ,
∴△BAD≌△ACE(AAS),
∴BD=AE,AD=CE,
又DE=AE+AD,
∴DE=BD+CE
(3)解:DE=CE﹣BD,
同(2)可得△BAD≌△ACE,
故BD=AE,AD=CE,
又DE=AD﹣AE,
∴DE=CE﹣BD
28. (1)证明:如图②,∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠ABD+∠CAF=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
∴△ABD≌△CAF(AAS)
(2)证明:如图③,
∵∠1=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,
∴∠ABE=∠CAF,
∵∠2=∠FCA+∠CAF,∠BAC=∠BAE+∠CAF,∠2=∠BAC,
∴∠BAE=∠FCA,
在△ABE和△CAF中, ,
∴△ABE≌△CAF(ASA)
(3)1
29. (1)证明:∵AE⊥AF,∠BAC=90°,
∴∠EAB=∠FAC
(2)解:△AEB与△AFC全等.
理由如下:在△EAB和△FAC中,
,
∴△EAB≌△FAC
(3)证明:由(2)得,△EAB≌△FAC,
∴∠ACF=∠ABE,
∵∠ACF+∠AHC=90°,∠AHC=∠FHB,
∴∠FHB+∠ABE=90°
∴CF⊥BE,又EF=FB,
∴CE=CB.
30. (1)解:探究:延长DA交BE于F.
∵△ABC和△CDE都为等腰直角三角形,∠ACB=∠ECD=90°.
∴BC=CA,EC=CD,
∴△BCE≌△ACD,
∴BE=AD,∠BEC=∠ADC,
∵∠ACB=90°,
∴∠BEC+∠EBC=90°,
∴∠ADC+∠EBC=90°,
∴∠BFD=90°,
∴BE⊥AD
(2)解:拓展:作FM⊥DE于M,FN⊥BE于N.
由探究可知:BE⊥DE,BE=AD=4,∠FEM=∠FEB=45°,
∵FM⊥DE于M,FN⊥BE于N.
∴FM=FN,
∵ EB?FN+ ?AE?FM= BE?AE,
∴FM=FN= ,
∴EF= ,
∵CE=CD=3 ,
∴CF= ,
∴EF:CF=4:5.
故答案为 .
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
