第2章 直线与圆的位置关系提高检测题(含答案)
文档属性
| 名称 | 第2章 直线与圆的位置关系提高检测题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教九下数学《直线与圆的位置关系》提高测试题
(难度中等以上,时间100分钟,满分100分)
选择题(共30分)
1.半径为10的⊙O和直线l上一点A,且OA=10,则直线l与⊙O的位置关系是( )
A.相切??????????? ?B.相交??????????? ??C.相离??????????? ?D.相切或相交
2.如图,直线AB与⊙O相切于点A,⊙O的半径为2.若∠OBA=30°,则OB的长为(?? )
A.?? B.4 ??? ?C. D.2
3.如图,从⊙O外一点P引⊙O的两条切线PA.PB,切点分别为A.B.如果∠APB=60°,PA=8,那么弦AB的长是(??? )
A.4 ?????B.8 ??????C.????? D.
4.边长为1正三角形的内切圆半径为( )
A.1? B.?????? C.?????? D.
5.已知直角三角形的两条直角边长分别为6和8,它的内切圆半径是( )
A.2??????????????B.2.4??????????? C.5??????????????D.6
6.如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知AD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是( )A.9cm???????????????????B.12cm???????????????????C.15cm?????????????????D.18cm
7.如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
A.40°????????????????????B.50°??????????????????????C.60°?????????????????????D.20°
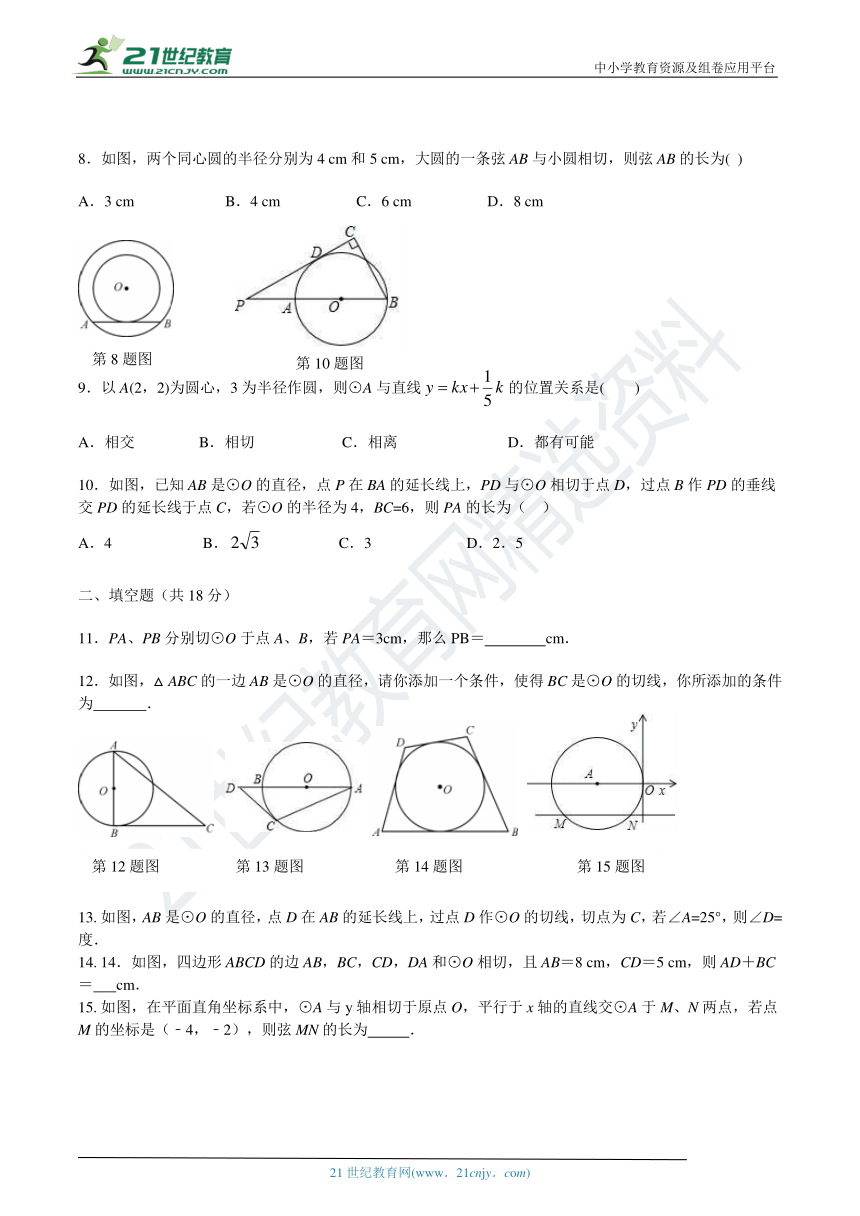
8.如图,两个同心圆的半径分别为4 cm和5 cm,大圆的一条弦AB与小圆相切,则弦AB的长为(??)
A.3 cm? ?? ? ?? B.4 cm? ?? ??? C.6 cm? ?? ??? D.8 cm
9.以A(2,2)为圆心,3为半径作圆,则⊙A与直线的位置关系是( )
A.相交? B.相切? C.相离? D.都有可能
10.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为( )A.4????????????????????????B.????????????????????C.3?????????????????????????D.2.5
填空题(共18分)
11.PA、PB分别切⊙O于点A、B,若PA=3cm,那么PB= cm.
12.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使得BC是⊙O的切线,你所添加的条件为??????????????.
?
如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D= 度.
14.如图,四边形ABCD的边AB,BC,CD,DA和⊙O相切,且AB=8 cm,CD=5 cm,则AD+BC=??????cm.
如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(﹣4,﹣2),则弦MN的长为 ??? .
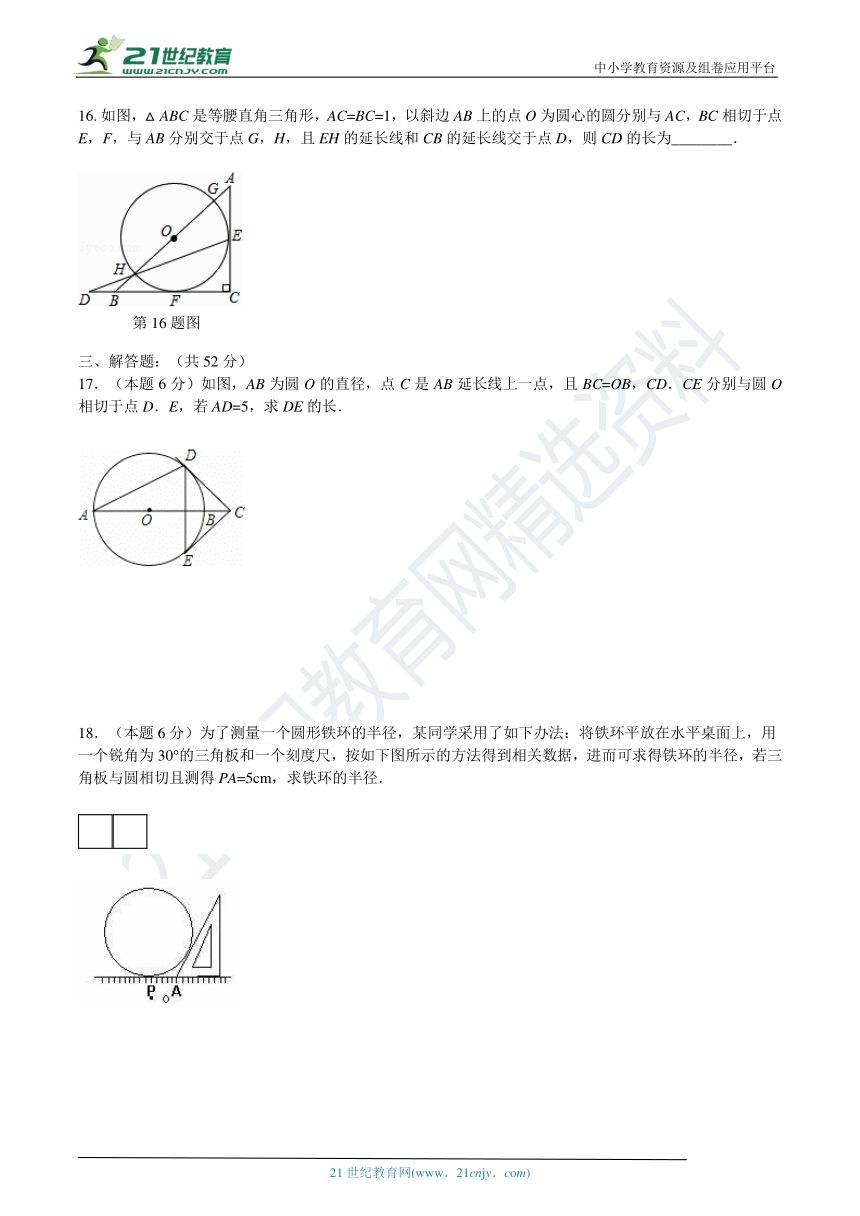
如图,△ABC是等腰直角三角形,AC=BC=1,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为________.
解答题:(共52分)
17.(本题6分)如图,AB为圆O的直径,点C是AB延长线上一点,且BC=OB,CD.CE分别与圆O相切于点D.E,若AD=5,求DE的长.
18.(本题6分)为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如下图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得PA=5cm,求铁环的半径.
19.(本题6分)如图,C是⊙O上一点,点P在直径AB的延长线上,⊙O的半径为3,PB=2,PC=4.
(1)求证:PC是⊙O的切线;
(2)求tan∠CAB的值.
20.(本题8分)如图,PA.PB是⊙O的切线,A.B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
21.(本题8分)如图,∠MAN=30°,点O为边AN上一点,以O为圆心,4为半径作⊙O交AN于D,E两点.
(1)当⊙O与AM相切时,求AD的长;
(2)如果AD=2,那么AM与⊙O又会有怎样的位置关系?并说明理由.
22.(本题8分)如图,⊙O?经过菱形?ABCD?的三个顶点?A、C、D,且与?AB?相切于点?A.
(1)???求证:BC?为⊙O?的切线;
(2)???求∠B?的度数.
23.(本题10分)如图,△ABC的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD于E,交AB于F,交⊙O于G.
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AF?AB;
(3)求若⊙O的直径为10,AC=2,求AE的长.
答案
选择题:DBBBA BBCAA
填空题:
11.3
如∠BAC=90°
40
13
3
解答题
17.连接OD,OE,AE,
?
∵CD.CE分别与圆O相切于点D.E,
∴∠ODC=∠OEC=90°,∵BC=OB,∴OC=2OD,∴∠DCO=30°,∴∠DCE=60°,∴∠DOE=120°,
∴∠DAE=60°,∵CD=CE,∠DCO=∠ECO,∴AC垂直平分DE,∴AD=AE,∴△ADE是等边三角形,
∴DE=AD=5.?
18.OP=
19.(1)如图,连接OC、BC∵⊙O的半径为3,PB=2∴OC=OB=3,OP=OB+PB=5∵PC=4
∴OC2+PC2=OP2∴△OCP是直角三角形,∴OC⊥P∴PC是⊙O的切线.
(2)∵AB是直径∴∠ACB=90°∴∠ACO+∠OCB=90°∵OC⊥PC
∴∠BCP+∠OCB=90°∴∠BCP=∠ACO∵OA=OC∴∠A=∠ACO∴∠A=∠BCP在△PBC和△PCA中:∠BCP=∠A,∠P=∠P∴△PBC∽△PCA,∴
20.(1)∵PA.PB是⊙O的切线,∴AP=BP,∵∠P=60°,∴∠PAB=60°,∵AC是⊙O的直径,∴∠PAC=90°,∴∠BAC=90°-60°=30°;
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,∴OP=4,由勾股定理得:AP=2,∵AP=BP,∠APB=60°,∴△APB是等边三角形,∴AB=AP=2.
21.(1)设AM与⊙O相切于点B,并连接OB,则OB⊥AB;
在△AOB中,∠A=30°,则AO=2OB=8,所以AD=AO﹣OD,即AD=4.
(2)AM与⊙O相交,理由如下:过点O作OF⊥AM于F,∴∠AFO=90°,OF=OA?sinA,AD=2,DO=4,
∴AO=AD+DO=6,且∠A=30°,∴OF=6?sin30°=3<4,∴AM与⊙O相交.
22.证明:连结?OA、OB、OC,∵AB?与⊙O?切于?A?点,∴OA⊥AB,即∠OAB=90°,
∵四边形?ABCD?为菱形,∴BA=BC,∴△ABO≌△CBO(SSS),∴∠BCO=∠BAO=90°,∴OC⊥BC,
∴BC?为⊙O?的切线;
(2)解:连接?BD,∵△ABO≌△CBO,∴∠ABO=∠CBO,∵四边形?ABCD?为菱形,∴BD?平分∠ABC,DA=DC,∴点?O?在?BD?上,∵∠BOC=2∠ODC, 而?CB=CD,∴∠OBC=∠ODC,∴∠BOC=2∠OBC,∵∠BOC+∠OBC=90°,∴∠OBC=30°,∴∠ABC=2∠OBC=60°.
23.PA与⊙O相切.
理由:连接CD,∵AD为⊙O的直径,∴∠ACD=90°∴∠D+∠CAD=90°∵∠B=∠D,∠PAC=∠B∴∠PAC=∠D,∴∠PAC+∠CAD=90°
即DA⊥PA∵点A在圆上,∴PA与⊙O相切.
(2)证明:连接BG∵AD为⊙O的直径,CG⊥AD∴AC弧与AG弧相等∴∠AGF=∠ABG
∵∠GAF=∠BAG∴△AGF∽△ABG∴AG:AB=AF:AG∴AG2=AB?AF
(3)解:∵AD是直径,CG⊥AD∴∠ACD=∠AEC=90°∵∠CAD=∠EAC∴△ACD∽△AEC
∴,即?AE=2
第2题图 第3题图 第6题图 第7题图
第8题图
第10题图
第12题图 第13题图 第14题图 第15题图
第16题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
