1.3 解直角三角形(1) 同步训练
图片预览



文档简介
初中数学浙教版九年级下册1.3 解直角三角形(1) 同步训练
一、基础夯实
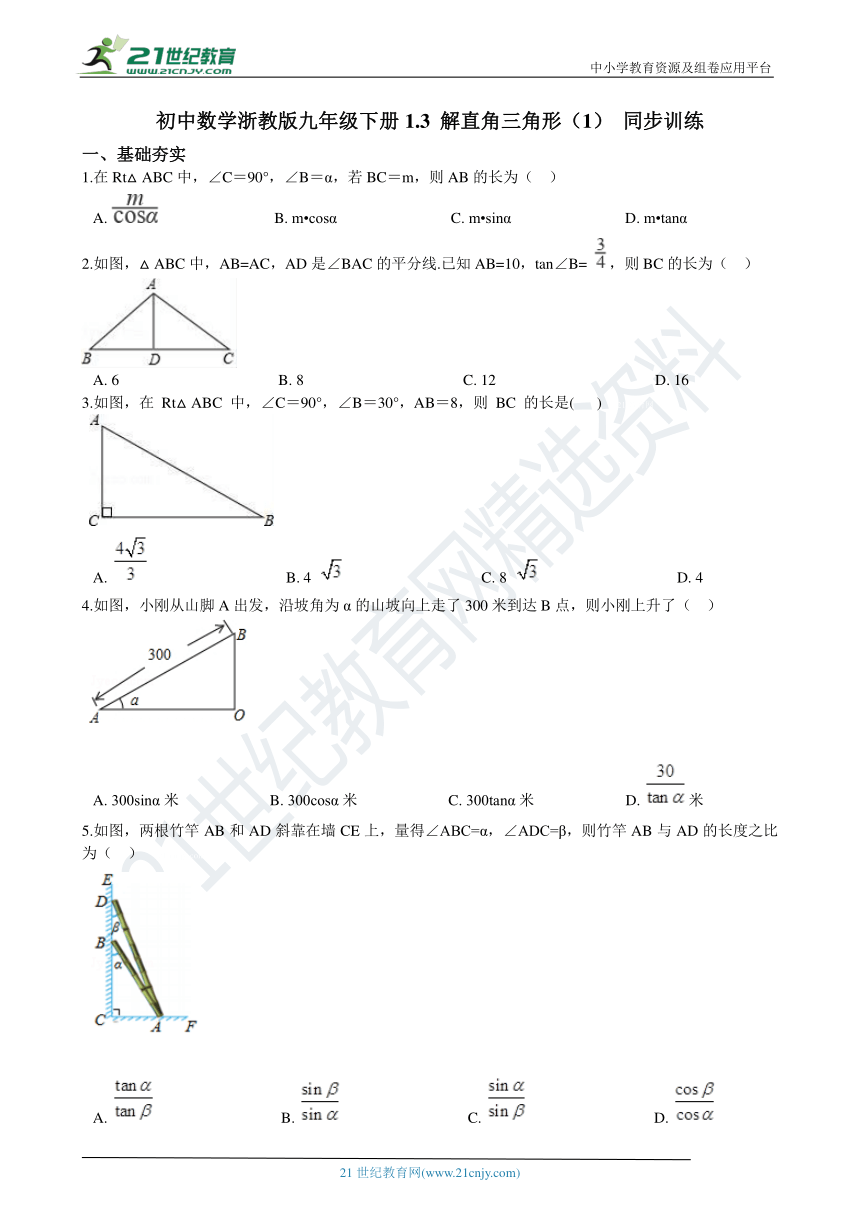
1.在Rt△ABC中,∠C=90°,∠B=α,若BC=m,则AB的长为(?? )
A.???????????????????????????????B.?m?cosα??????????????????????????????C.?m?sinα??????????????????????????????D.?m?tanα
2.如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=10,tan∠B= ,则BC的长为(?? )
A.?6??????????????????????????????????????????B.?8??????????????????????????????????????????C.?12??????????????????????????????????????????D.?16
3.如图,在 Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则 BC 的长是(???? ) 21教育网
A.?????????????????????????????????????B.?4 ????????????????????????????????????C.?8 ????????????????????????????????????D.?4
4.如图,小刚从山脚A出发,沿坡角为α的山坡向上走了300米到达B点,则小刚上升了(?? )
A.?300sinα米????????????????????????B.?300cosα米????????????????????????C.?300tanα米????????????????????????D.?米
5.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为(?? ) 21·cn·jy·com
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
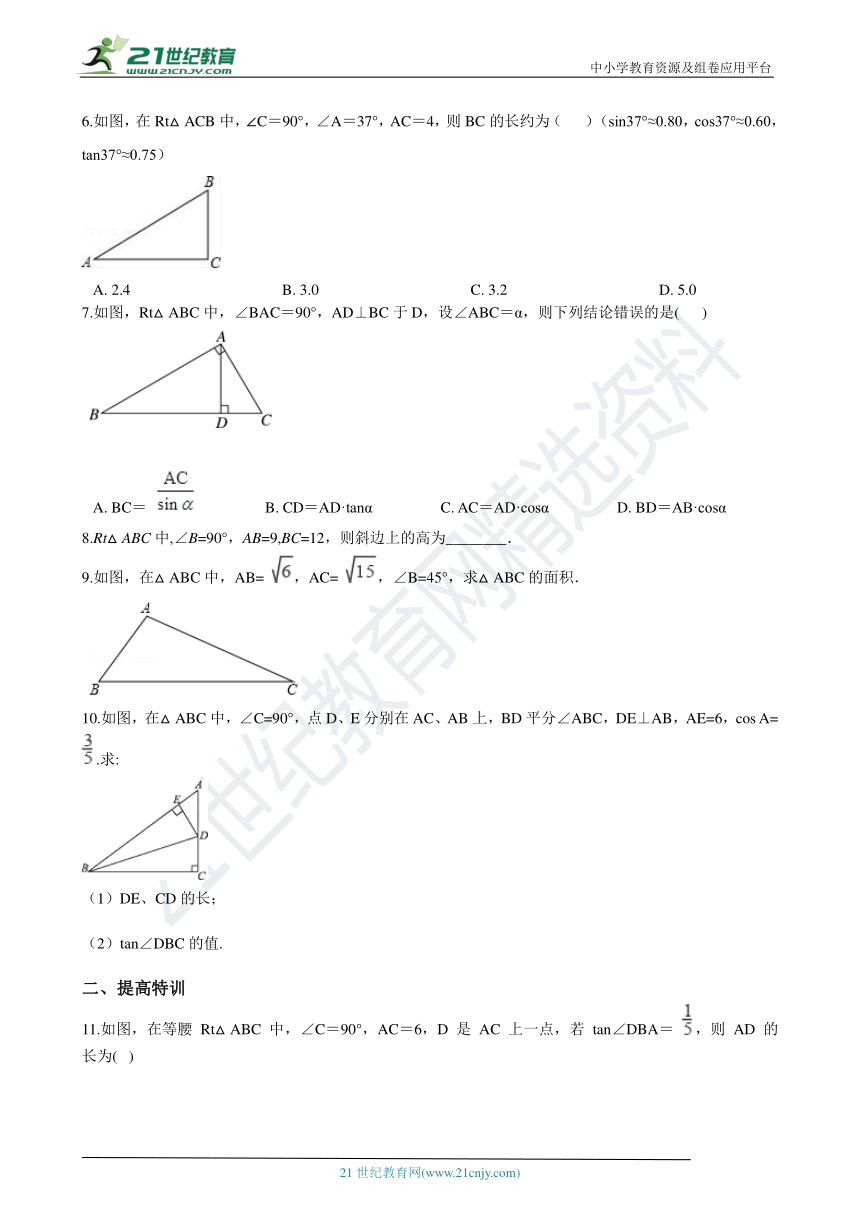
6.如图,在Rt△ACB中,∠C=90°,∠A=37°,AC=4,则BC的长约为(???? )(sin37°≈0.80,cos37°≈0.60,tan37°≈0.75) www.21-cn-jy.com
A.?2.4????????????????????????????????????????B.?3.0????????????????????????????????????????C.?3.2????????????????????????????????????????D.?5.0
7.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( ????)
A.?BC= ??????????????????B.?CD=AD·tanα??????????????????C.?AC=AD·cosα??????????????????D.?BD=AB·cosα
8.Rt△ABC中,∠B=90°,AB=9,BC=12,则斜边上的高为________.
9.如图,在△ABC中,AB= ,AC= ,∠B=45°,求△ABC的面积.
10.如图,在△ABC中,∠C=90°,点D、E分别在AC、AB上,BD平分∠ABC,DE⊥AB,AE=6,cos A= .求:2·1·c·n·j·y
(1)DE、CD的长;
(2)tan∠DBC的值.
二、提高特训
11.如图,在等腰 Rt△ABC 中,∠C=90°,AC=6,D 是 AC 上一点,若 tan∠DBA= ,则 AD 的长为(? ) 21·世纪*教育网
A.?2?????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?1
12.如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC﹣CB运动,到点B停止,过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5秒时,PD的长是(?? ) 2-1-c-n-j-y
A.?2cm??????????????????????????????????B.?1.8cm??????????????????????????????????C.?1.5cm??????????????????????????????????D.?1.2cm
13.如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为(?? ) 【出处:21教育名师】
A.?50m?????????????????????B.?25m?????????????????????C.?(50﹣ )m?????????????????????D.?(50﹣25 )m
14.如图1,含30°和45°角的两块三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm,点P为边BC(EF)的中点,现将三角板ABC绕点P按逆时针方向旋转角度α(如图2),设边AB与EF相交于点Q,则当a从0°到90°的变化过程中,点Q移动的路径长为________(结果保留根号)
15.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2 米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为________米(结果保留根号). 【来源:21cnj*y.co*m】
16.在△ABC中,AB=6,AC=8,S△ABC=12 ,则∠A=________.
17.共享单车被誉为“新四大发明”之一,如图1所示是某公司2017年向信阳市场提供一种共享自行车的实物图,车架档AC与CD的长分别为45cm,60cm,AC⊥CD,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.(结果精确到1cm,参考数据:sin75°=0.9659,cos75°=0.2588,tan75°=3.7321)
18.如图1是某品牌订书机,其截面示意图如图2所示.订书钉放置在轨槽CD内的MD处,由连接弹簧的推动器MN推紧,连杆EP一端固定在压柄CF上的点E处,另一端P在DM上移动.当点P与点M重合后,拉动压柄CF会带动推动器MN向点C移动.使用时,压柄CF的端点F与出钉口D重合,纸张放置在底座AB的合适位置下压完成装订(即点D与点H重合).已知CA⊥AB,CA=2cm,AH=12cm,CE=5cm,EP=6cm,MN=2cm.
(1)求轨槽CD的长(结果精确到0.1);
(2)装入订书钉需打开压柄FC,拉动推动器MN向点C移动,当∠FCD=53°时,能否在ND处装入一段长为2.5cm的订书钉?(参考数据: ≈2.24, ≈6.08,sin53°≈0.80,cos53°≈0.60)
答案解析部分
一、基础夯实
1. A
解:如图所示:
∵ ,
∴AB= ,
故答案为:A.
【分析】由题意可知,△ABC为直角三角形,再由锐角三角函数的定义可知,角α的余弦=, 即cosα=, 整理即可求得AB的长。21cnjy.com
2. D
∵AB=AC,
∴BD=CD,
∵tan∠B= ,
∴AD= ,
∵AD2+BD2=AB2 ,
∴( )2+BD2=102 ,
∴BD=8,
∴BC=16;
故答案为:D.
【分析】在直角三角形ABD中,根据tan∠B=可将AD用含BD的代数式表示,再由勾股定理可得AD2+BD2=AB2可得关于BD的方程,解方程可求得BD的值,由题意得BC=2BD可求解。
3. B
解:在Rt△ABC中,cosB=
则BC = AB cosB = 8 cos30 =8 ? = .
故答案为:B.
【分析】根据cosB=即可求解。?
4. A
解: 在Rt△AOB中,∠AOB=90°,AB=300米,
BO=AB?sinα=300sinα米.
故答案为:A.
【分析】在Rt△AOB中,根据sinα=即可求解。
5. B
解: 在Rt△ABC中,AB= ,
在Rt△ACD中,AD= ,
∴AB:AD= : = ,
故答案为:B.
【分析】由图知,sinα=, 则AB=;在Rt△ACD中,sinβ=? ,则AD= ,所以AB:AD可求解。www-2-1-cnjy-com
6. B
解:在Rt△ACB中,tanA= ,
则BC=AC?tanA≈4×0.75=3.0,
故答案为:B.
【分析】在Rt△ACB中,根据tanA= 变形得,BC=AC?tanA,把AC和tanA的值代入计算即可求解。
7. C
解:在直角三角形ABC中,sinα==, 即BC=, 所以A选项正确; 在三角形ABC中,因为∠B+∠BAD=∠CAD+∠BAD,所以∠B=∠CAD=α,所以tan∠CAD=tanα=, 即CD=AD·?tanα,所以B选项正确; 在三角形ACD中,cosα=, 即AC=, 所以C选项错误,符合题意; 在三角形ABD中,cosα=, 即BD=AB·cosα,所以D选项正确。 故答案为:C。 21教育名师原创作品
【分析】在三角形中,根据每个选项的要求,求出对应角的正弦、余弦或正切,进行适当的变形即可证明选项的对错。21*cnjy*com
8.
Rt△ABC中,∠B=90°,AB=9,BC=12,所以斜边AC=15,
SRt△ABC= AB·BC=54
所以斜边上的高为
故填
【分析】根据三角形的面积表达方法,可解出斜边上的高。
9.解: 作AD⊥BC,垂足为D,
在Rt△ABD中,∠B=45°,
∴BD=AD=AB?sin45°= × = ,
在Rt△ACD中,AD= ,AC= ,
∴CD= =2 ,
∴BC=BD+CD=3 ,
∴S△ABC= BC?AD= ×3 × = .
【分析】由题意,作AD⊥BC,垂足为D,则 △ABD 是等腰直角三角形,所以根据 sin45°= 可求得BD=AD的值, 在Rt△ACD中 ,用勾股定理可求得CD的值,所以BC=BD+CD, S△ABC=??BC?AD 可求解。21*cnjy*com
10. (1)解:∵DE⊥AB,∴∠DEA=90°.在Rt△AED中,cos A=? ,即 =.∴AD=10.
根据勾股定理得DE=? =? =8.
又∵DE⊥AB,DC⊥BC,BD平分∠ABC,∴DC=DE=8.
(2)解:由(1)可得AC=AD+DC=10+8=18,在Rt△ABC中,cos A=,即? =? ,∴AB=30.根据勾股定理得BC=? =? =24.
∴在Rt△BCD中,tan ∠DBC===? .
【分析】(1)在Rt△AED中,cos A=,可求出AD,再由勾股定理求出DE,根据角平分线的性质可得CD=DE; (2)根据(1)可得AC=AD+DC,求出AC,而在Rt△ABC中,cos A=求出AB,再由勾股定理求出BC,而在Rt△BCD中,tan ∠DBC=?, 代入DC,BC的值即可求出。
二、提高特训
11. A
如图,作DE⊥AB于E.
∵tan∠DBA= = ,∴BE=5DE.∵△ABC为等腰直角三角形,∴∠A=45°,∴AE=DE.∴BE=5AE,又∵AC=6,∴AB=6 ,∴AE+BE=AE+5AE=6 ,∴AE= ,∴在等腰直角△ADE中,由勾股定理,得AD= ,AE=2.【版权所有:21教育】
故答案为:A. 【分析】作DE⊥AB于E.用勾股定理可求得AB的长;解直角三角形BDE可得tan∠DBA= = , 则BE=5DE;而AB=AE+BE可求出AE的值,而三角形ADE是等腰直角三角形,解这个等腰直角三角形即可求得AD的值。
12. D
由图2可得,AC=3,BC=4,当t=5时,如图所示:
,
此时AC+CP=5,故BP=AC+BC﹣AC﹣CP=2,∵sin∠B= ,∴PD=BPsin∠B= cm.故答案为:D.
【分析】有线段的构成得BP=AC+BC﹣AC﹣CP可求得BP的值,然后根据sin∠B==可求解.
13. C
解:过点A作AM⊥DC于点M,过点B作BN⊥DC于点N ∴AB=MN,AM=BN 在直角三角形ACM中,即可得到CD=AM=50 在直角三角形BCN中 ∵∠BCN=∠ACB+∠ACD=60°,BN=50 ∴CN== ∴MN=CM-CN=50- ∴AB=MN=50-。 故答案为:C。 【分析】过点A作AM⊥DC于点M,过点B作BN⊥DC于点N,通过解直角三角形分别求出CM和CN的长度,求出MN=AB。
14. (6﹣2 )cm
解:当a从0°到90°的变化过程中,Q点从E运动到Q,(如图)
∵EF=12cm,
∴BP=6cm,
∵∠B=30°,
在Rt△BPQ中,QP=2 cm,
∴EQ=(6﹣2 )cm,
∴Q点移动的路径为(6﹣2 )cm,
故答案为(6﹣2 )cm;
【分析】由题意知:当a从0°到90°的变化过程中,Q点从E运动到Q,即只需求出EQ的值即可。在Rt△BPQ中,解直角三角形可求得QP的长,再结合线段的构成得EQ=EP-PQ=EF-PQ可求解.
15.
解:如图所示:
AB=2 米,∠ACB=60°,∠DCE=45°,AC=CE.
则在直角三角形ABC中,
=tan∠ACB=tan60°= ,
=sin∠ACB=sin60°= ,
∴BC= = =2,AC= = =4,
∴直角三角形DCE中,CE=AC=4,
∴ =cos45°= ,
∴CD=CE× =4× =2 ,
∴BD=2+2 ,
故答案为:2+2 .
【分析】AB=2 米,∠ACB=60°,∠DCE=45°,AC=CE,利用解直角三角形分别求出BC,AC的长;再在Rt△DCE中,利用解直角三角形求出CD,然后求出BD的长。【来源:21·世纪·教育·网】
16. 60°或120°
解:过点C作CD⊥AB于点D,
如图1,当△ABC为锐角三角形时,
∵S△ABC= AB?CD,且AB=6、S△ABC=12 ,
∴CD= = =4 ,
在Rt△ACD中,∵sinA= = = ,
∴∠A=60°;
如图2,当△ABC为钝角三角形时,
由①知,CD=4 ,
∵sin∠DAC= = = ,
∴∠DAC=60°,
则∠BAC=120°,
故答案为:60°或120°.
【分析】此题没有告诉我们三角形的形状,故要分情况讨论。 ①若∠A为90°,则S△ABC=, 与题意不符,故∠A只能是锐角或钝角。 ②当∠A为锐角时,如图1,根据S△ABC的计算公式反求出CD,在Rt△ACD中,解直角三角形可得∠A=60°。 ③当∠A为钝角时,如图2,同理②可得∠DAC=60°,根据补角的定义可得∠BAC=180°-∠DAC=120°。
17.(1)解:∵AC⊥CD,AC=45cm,CD=60cm,
∴AD= (cm),
即车架档AD的长是75cm
(2)解:作EF⊥AB于点F,如图所示,
∵AC=45cm,EC=20cm,∠EAB=75°,
∴EF=AE?sin75°=(45+20)×0.9659≈63cm,
即车座点E到车架档AB的距离是63cm
【分析】(1)用勾股定理即可求解; (2)解直角三角形AEF即可求解。
18. (1)解:由题意CD=CH,
在Rt△ACH中,CH= =2 ≈12.2(cm).
∴CD=CH=12.6(cm)
(2)解:如图2中,作EK⊥PC于K.
在Rt△ECK中,EK=EC?sin53°≈4(cm),CK=EC?cos53°≈3(cm),
在Rt△EPK中,PK= = =2 ≈4.48(cm),
∴DP=CD﹣CK﹣PK﹣MN=12.6﹣3﹣4.48﹣2=3.12>2.5,
∴能在ND处装入一段长为2.5cm的订书钉.
【分析】(1)由题意CD=CH,要求出CD的长,只需求出CH即可。 在Rt△ACH中,由勾股定理即可求解; (2)作EK⊥PC于K, 在Rt△ECK中,解直角三角形可求得EK和CK的长; 解直角三角形EPK可求得PK的长,由线段的构成得DP=CD-CK-PK-MN可求得PD的值,与订书钉的长度比较大小即可判断求解。21世纪教育网版权所有
一、基础夯实
1.在Rt△ABC中,∠C=90°,∠B=α,若BC=m,则AB的长为(?? )
A.???????????????????????????????B.?m?cosα??????????????????????????????C.?m?sinα??????????????????????????????D.?m?tanα
2.如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=10,tan∠B= ,则BC的长为(?? )
A.?6??????????????????????????????????????????B.?8??????????????????????????????????????????C.?12??????????????????????????????????????????D.?16
3.如图,在 Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则 BC 的长是(???? ) 21教育网
A.?????????????????????????????????????B.?4 ????????????????????????????????????C.?8 ????????????????????????????????????D.?4
4.如图,小刚从山脚A出发,沿坡角为α的山坡向上走了300米到达B点,则小刚上升了(?? )
A.?300sinα米????????????????????????B.?300cosα米????????????????????????C.?300tanα米????????????????????????D.?米
5.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为(?? ) 21·cn·jy·com
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
6.如图,在Rt△ACB中,∠C=90°,∠A=37°,AC=4,则BC的长约为(???? )(sin37°≈0.80,cos37°≈0.60,tan37°≈0.75) www.21-cn-jy.com
A.?2.4????????????????????????????????????????B.?3.0????????????????????????????????????????C.?3.2????????????????????????????????????????D.?5.0
7.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( ????)
A.?BC= ??????????????????B.?CD=AD·tanα??????????????????C.?AC=AD·cosα??????????????????D.?BD=AB·cosα
8.Rt△ABC中,∠B=90°,AB=9,BC=12,则斜边上的高为________.
9.如图,在△ABC中,AB= ,AC= ,∠B=45°,求△ABC的面积.
10.如图,在△ABC中,∠C=90°,点D、E分别在AC、AB上,BD平分∠ABC,DE⊥AB,AE=6,cos A= .求:2·1·c·n·j·y
(1)DE、CD的长;
(2)tan∠DBC的值.
二、提高特训
11.如图,在等腰 Rt△ABC 中,∠C=90°,AC=6,D 是 AC 上一点,若 tan∠DBA= ,则 AD 的长为(? ) 21·世纪*教育网
A.?2?????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?1
12.如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC﹣CB运动,到点B停止,过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5秒时,PD的长是(?? ) 2-1-c-n-j-y
A.?2cm??????????????????????????????????B.?1.8cm??????????????????????????????????C.?1.5cm??????????????????????????????????D.?1.2cm
13.如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为(?? ) 【出处:21教育名师】
A.?50m?????????????????????B.?25m?????????????????????C.?(50﹣ )m?????????????????????D.?(50﹣25 )m
14.如图1,含30°和45°角的两块三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm,点P为边BC(EF)的中点,现将三角板ABC绕点P按逆时针方向旋转角度α(如图2),设边AB与EF相交于点Q,则当a从0°到90°的变化过程中,点Q移动的路径长为________(结果保留根号)
15.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2 米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为________米(结果保留根号). 【来源:21cnj*y.co*m】
16.在△ABC中,AB=6,AC=8,S△ABC=12 ,则∠A=________.
17.共享单车被誉为“新四大发明”之一,如图1所示是某公司2017年向信阳市场提供一种共享自行车的实物图,车架档AC与CD的长分别为45cm,60cm,AC⊥CD,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.(结果精确到1cm,参考数据:sin75°=0.9659,cos75°=0.2588,tan75°=3.7321)
18.如图1是某品牌订书机,其截面示意图如图2所示.订书钉放置在轨槽CD内的MD处,由连接弹簧的推动器MN推紧,连杆EP一端固定在压柄CF上的点E处,另一端P在DM上移动.当点P与点M重合后,拉动压柄CF会带动推动器MN向点C移动.使用时,压柄CF的端点F与出钉口D重合,纸张放置在底座AB的合适位置下压完成装订(即点D与点H重合).已知CA⊥AB,CA=2cm,AH=12cm,CE=5cm,EP=6cm,MN=2cm.
(1)求轨槽CD的长(结果精确到0.1);
(2)装入订书钉需打开压柄FC,拉动推动器MN向点C移动,当∠FCD=53°时,能否在ND处装入一段长为2.5cm的订书钉?(参考数据: ≈2.24, ≈6.08,sin53°≈0.80,cos53°≈0.60)
答案解析部分
一、基础夯实
1. A
解:如图所示:
∵ ,
∴AB= ,
故答案为:A.
【分析】由题意可知,△ABC为直角三角形,再由锐角三角函数的定义可知,角α的余弦=, 即cosα=, 整理即可求得AB的长。21cnjy.com
2. D
∵AB=AC,
∴BD=CD,
∵tan∠B= ,
∴AD= ,
∵AD2+BD2=AB2 ,
∴( )2+BD2=102 ,
∴BD=8,
∴BC=16;
故答案为:D.
【分析】在直角三角形ABD中,根据tan∠B=可将AD用含BD的代数式表示,再由勾股定理可得AD2+BD2=AB2可得关于BD的方程,解方程可求得BD的值,由题意得BC=2BD可求解。
3. B
解:在Rt△ABC中,cosB=
则BC = AB cosB = 8 cos30 =8 ? = .
故答案为:B.
【分析】根据cosB=即可求解。?
4. A
解: 在Rt△AOB中,∠AOB=90°,AB=300米,
BO=AB?sinα=300sinα米.
故答案为:A.
【分析】在Rt△AOB中,根据sinα=即可求解。
5. B
解: 在Rt△ABC中,AB= ,
在Rt△ACD中,AD= ,
∴AB:AD= : = ,
故答案为:B.
【分析】由图知,sinα=, 则AB=;在Rt△ACD中,sinβ=? ,则AD= ,所以AB:AD可求解。www-2-1-cnjy-com
6. B
解:在Rt△ACB中,tanA= ,
则BC=AC?tanA≈4×0.75=3.0,
故答案为:B.
【分析】在Rt△ACB中,根据tanA= 变形得,BC=AC?tanA,把AC和tanA的值代入计算即可求解。
7. C
解:在直角三角形ABC中,sinα==, 即BC=, 所以A选项正确; 在三角形ABC中,因为∠B+∠BAD=∠CAD+∠BAD,所以∠B=∠CAD=α,所以tan∠CAD=tanα=, 即CD=AD·?tanα,所以B选项正确; 在三角形ACD中,cosα=, 即AC=, 所以C选项错误,符合题意; 在三角形ABD中,cosα=, 即BD=AB·cosα,所以D选项正确。 故答案为:C。 21教育名师原创作品
【分析】在三角形中,根据每个选项的要求,求出对应角的正弦、余弦或正切,进行适当的变形即可证明选项的对错。21*cnjy*com
8.
Rt△ABC中,∠B=90°,AB=9,BC=12,所以斜边AC=15,
SRt△ABC= AB·BC=54
所以斜边上的高为
故填
【分析】根据三角形的面积表达方法,可解出斜边上的高。
9.解: 作AD⊥BC,垂足为D,
在Rt△ABD中,∠B=45°,
∴BD=AD=AB?sin45°= × = ,
在Rt△ACD中,AD= ,AC= ,
∴CD= =2 ,
∴BC=BD+CD=3 ,
∴S△ABC= BC?AD= ×3 × = .
【分析】由题意,作AD⊥BC,垂足为D,则 △ABD 是等腰直角三角形,所以根据 sin45°= 可求得BD=AD的值, 在Rt△ACD中 ,用勾股定理可求得CD的值,所以BC=BD+CD, S△ABC=??BC?AD 可求解。21*cnjy*com
10. (1)解:∵DE⊥AB,∴∠DEA=90°.在Rt△AED中,cos A=? ,即 =.∴AD=10.
根据勾股定理得DE=? =? =8.
又∵DE⊥AB,DC⊥BC,BD平分∠ABC,∴DC=DE=8.
(2)解:由(1)可得AC=AD+DC=10+8=18,在Rt△ABC中,cos A=,即? =? ,∴AB=30.根据勾股定理得BC=? =? =24.
∴在Rt△BCD中,tan ∠DBC===? .
【分析】(1)在Rt△AED中,cos A=,可求出AD,再由勾股定理求出DE,根据角平分线的性质可得CD=DE; (2)根据(1)可得AC=AD+DC,求出AC,而在Rt△ABC中,cos A=求出AB,再由勾股定理求出BC,而在Rt△BCD中,tan ∠DBC=?, 代入DC,BC的值即可求出。
二、提高特训
11. A
如图,作DE⊥AB于E.
∵tan∠DBA= = ,∴BE=5DE.∵△ABC为等腰直角三角形,∴∠A=45°,∴AE=DE.∴BE=5AE,又∵AC=6,∴AB=6 ,∴AE+BE=AE+5AE=6 ,∴AE= ,∴在等腰直角△ADE中,由勾股定理,得AD= ,AE=2.【版权所有:21教育】
故答案为:A. 【分析】作DE⊥AB于E.用勾股定理可求得AB的长;解直角三角形BDE可得tan∠DBA= = , 则BE=5DE;而AB=AE+BE可求出AE的值,而三角形ADE是等腰直角三角形,解这个等腰直角三角形即可求得AD的值。
12. D
由图2可得,AC=3,BC=4,当t=5时,如图所示:
,
此时AC+CP=5,故BP=AC+BC﹣AC﹣CP=2,∵sin∠B= ,∴PD=BPsin∠B= cm.故答案为:D.
【分析】有线段的构成得BP=AC+BC﹣AC﹣CP可求得BP的值,然后根据sin∠B==可求解.
13. C
解:过点A作AM⊥DC于点M,过点B作BN⊥DC于点N ∴AB=MN,AM=BN 在直角三角形ACM中,即可得到CD=AM=50 在直角三角形BCN中 ∵∠BCN=∠ACB+∠ACD=60°,BN=50 ∴CN== ∴MN=CM-CN=50- ∴AB=MN=50-。 故答案为:C。 【分析】过点A作AM⊥DC于点M,过点B作BN⊥DC于点N,通过解直角三角形分别求出CM和CN的长度,求出MN=AB。
14. (6﹣2 )cm
解:当a从0°到90°的变化过程中,Q点从E运动到Q,(如图)
∵EF=12cm,
∴BP=6cm,
∵∠B=30°,
在Rt△BPQ中,QP=2 cm,
∴EQ=(6﹣2 )cm,
∴Q点移动的路径为(6﹣2 )cm,
故答案为(6﹣2 )cm;
【分析】由题意知:当a从0°到90°的变化过程中,Q点从E运动到Q,即只需求出EQ的值即可。在Rt△BPQ中,解直角三角形可求得QP的长,再结合线段的构成得EQ=EP-PQ=EF-PQ可求解.
15.
解:如图所示:
AB=2 米,∠ACB=60°,∠DCE=45°,AC=CE.
则在直角三角形ABC中,
=tan∠ACB=tan60°= ,
=sin∠ACB=sin60°= ,
∴BC= = =2,AC= = =4,
∴直角三角形DCE中,CE=AC=4,
∴ =cos45°= ,
∴CD=CE× =4× =2 ,
∴BD=2+2 ,
故答案为:2+2 .
【分析】AB=2 米,∠ACB=60°,∠DCE=45°,AC=CE,利用解直角三角形分别求出BC,AC的长;再在Rt△DCE中,利用解直角三角形求出CD,然后求出BD的长。【来源:21·世纪·教育·网】
16. 60°或120°
解:过点C作CD⊥AB于点D,
如图1,当△ABC为锐角三角形时,
∵S△ABC= AB?CD,且AB=6、S△ABC=12 ,
∴CD= = =4 ,
在Rt△ACD中,∵sinA= = = ,
∴∠A=60°;
如图2,当△ABC为钝角三角形时,
由①知,CD=4 ,
∵sin∠DAC= = = ,
∴∠DAC=60°,
则∠BAC=120°,
故答案为:60°或120°.
【分析】此题没有告诉我们三角形的形状,故要分情况讨论。 ①若∠A为90°,则S△ABC=, 与题意不符,故∠A只能是锐角或钝角。 ②当∠A为锐角时,如图1,根据S△ABC的计算公式反求出CD,在Rt△ACD中,解直角三角形可得∠A=60°。 ③当∠A为钝角时,如图2,同理②可得∠DAC=60°,根据补角的定义可得∠BAC=180°-∠DAC=120°。
17.(1)解:∵AC⊥CD,AC=45cm,CD=60cm,
∴AD= (cm),
即车架档AD的长是75cm
(2)解:作EF⊥AB于点F,如图所示,
∵AC=45cm,EC=20cm,∠EAB=75°,
∴EF=AE?sin75°=(45+20)×0.9659≈63cm,
即车座点E到车架档AB的距离是63cm
【分析】(1)用勾股定理即可求解; (2)解直角三角形AEF即可求解。
18. (1)解:由题意CD=CH,
在Rt△ACH中,CH= =2 ≈12.2(cm).
∴CD=CH=12.6(cm)
(2)解:如图2中,作EK⊥PC于K.
在Rt△ECK中,EK=EC?sin53°≈4(cm),CK=EC?cos53°≈3(cm),
在Rt△EPK中,PK= = =2 ≈4.48(cm),
∴DP=CD﹣CK﹣PK﹣MN=12.6﹣3﹣4.48﹣2=3.12>2.5,
∴能在ND处装入一段长为2.5cm的订书钉.
【分析】(1)由题意CD=CH,要求出CD的长,只需求出CH即可。 在Rt△ACH中,由勾股定理即可求解; (2)作EK⊥PC于K, 在Rt△ECK中,解直角三角形可求得EK和CK的长; 解直角三角形EPK可求得PK的长,由线段的构成得DP=CD-CK-PK-MN可求得PD的值,与订书钉的长度比较大小即可判断求解。21世纪教育网版权所有
