1.3 解直角三角形(3) 同步训练
图片预览

文档简介
初中数学浙教版九年级下册1.3 解直角三角形(3) 同步训练
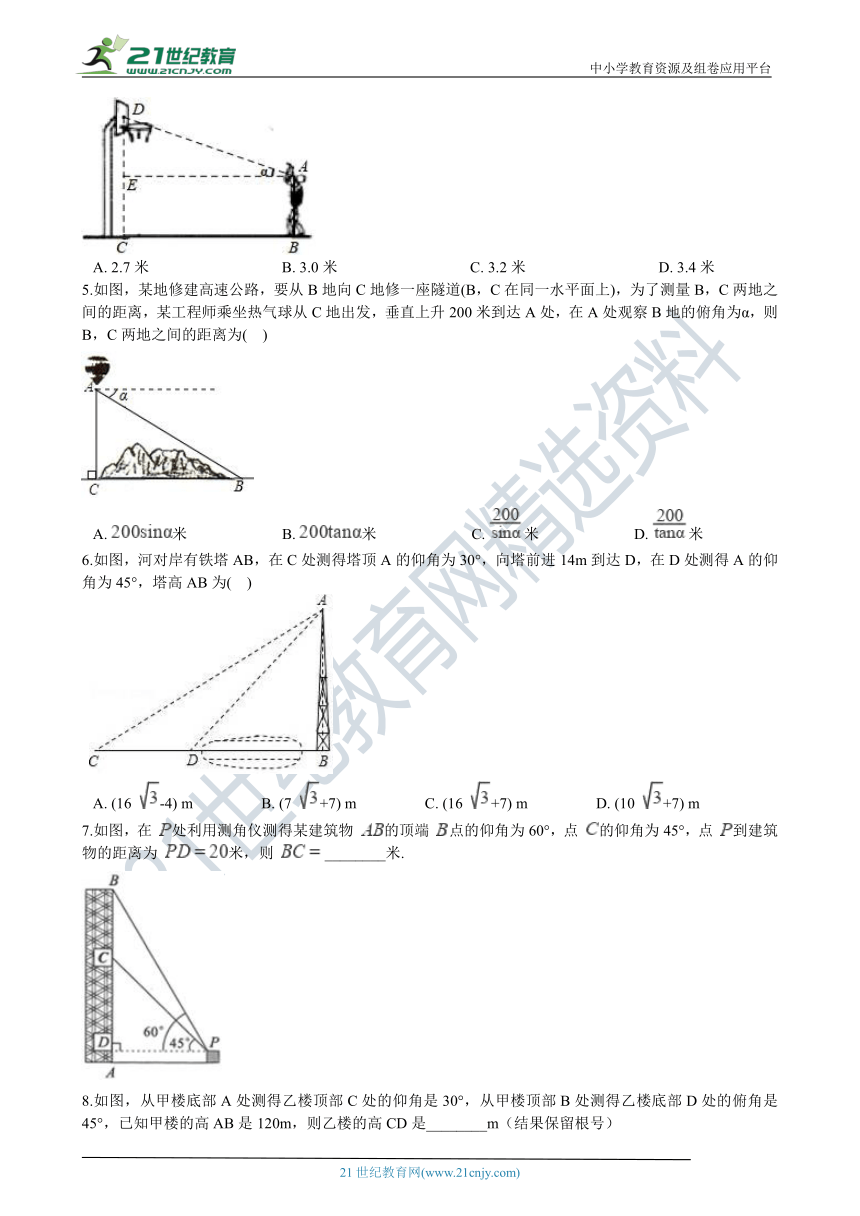
一、基础夯实
1.如图,护林员在离树8m的A处测得树顶B的仰角为45°,已知护林员的眼睛离地面的距离AC为1.6m,则树的高度BD为(?? ) 21教育网
A.?8m???????????????????????????B.?9.6m???????????????????????????C.?(4 +1.6)m???????????????????????????D.?(8 +1.6)m
2.南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为(???? ) 2·1·c·n·j·y
A.?asinα+asinβ??????????????????B.?acosα+acosβ??????????????????C.?atanα+atanβ??????????????????D.?
3.如图,某同学在距离建筑中心B点m米的点A处,测得旗杆底部点C的仰角为α,旗杆顶部点D的仰角为β,则旗杆CD的长为( ??) 21·世纪*教育网
A.?????????????????B.?mtanβ﹣mtanα????????????????C.?????????????????D.?msinβ﹣msinα
4.小明在某次投篮中刚好把球打到篮板的点D处后进球,已知小明与篮框底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为∠α,已知tanα= ,则点D到地面的距离CD是(?? )
A.?2.7米???????????????????????????????????B.?3.0米???????????????????????????????????C.?3.2米???????????????????????????????????D.?3.4米
5.如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升200米到达A处,在A处观察B地的俯角为α,则B,C两地之间的距离为(?? ) 【版权所有:21教育】
A.?米?????????????????????????B.?米?????????????????????????C.?米?????????????????????????D.?米
6.如图,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14m到达D,在D处测得A的仰角为45°,塔高AB为(?? )
A.?(16 -4) m??????????????????B.?(7 +7) m??????????????????C.?(16 +7) m??????????????????D.?(10 +7) m
7.如图,在 处利用测角仪测得某建筑物 的顶端 点的仰角为60°,点 的仰角为45°,点 到建筑物的距离为 米,则 ________米.
8.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是________m(结果保留根号)
9.如图,在某街道路边有相距10m、高度相同的两盏路灯(灯杆垂直地面),小明为了测量路灯的高度,在地面A处测得路灯PQ的顶端仰角为14°,向前行走25m到达B处,在地面测得路灯MN的顶端仰角为24.3°,已知点A,B,Q,N在同一条直线上,请你利用所学知识帮助小明求出路灯的高度.(结果精确到0.1m.参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,sin24.3°≈0.41,cos24.3°≈0.91,tan24.3°≈0.45)
10.某居民小区物业要在广场树立一个“扫黑除恶,共创和谐”的矩形电子灯牌,如图所示,施工人员在两侧加固合金框架,已知合金框架底端G距广告牌立柱FD的距离GD=4米,从G点测得广告牌顶端F点和底端E点的仰角分别是60°和45°.
(1)若AF长为5米,求灯牌的面积;
(2)求两侧加固的铝合金框架总共用料多少米?(本题中的计算过程和结果均保留根号)
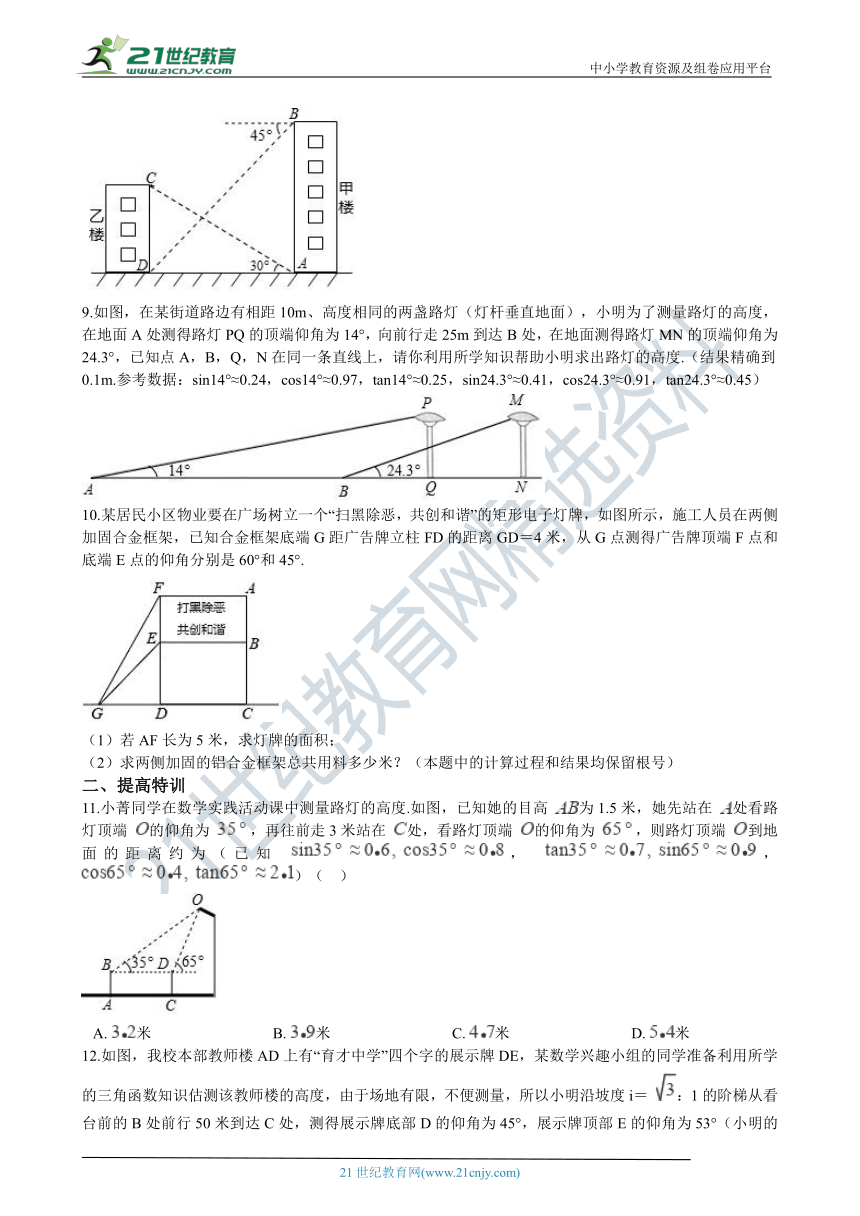
二、提高特训
11.小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高 为1.5米,她先站在 处看路灯顶端 的仰角为 ,再往前走3米站在 处,看路灯顶端 的仰角为 ,则路灯顶端 到地面的距离约为(已知 , , )(?? )
A.?米????????????????????????????????B.?米????????????????????????????????C.?米????????????????????????????????D.?米
12.如图,我校本部教师楼AD上有“育才中学”四个字的展示牌DE,某数学兴趣小组的同学准备利用所学的三角函数知识估测该教师楼的高度,由于场地有限,不便测量,所以小明沿坡度i= :1的阶梯从看台前的B处前行50米到达C处,测得展示牌底部D的仰角为45°,展示牌顶部E的仰角为53°(小明的身高忽略不计),已知展示牌高DE=15米,则该教师楼AD的高度约为(?? )米.(参考数据:Sin37°≈0,6,cos 37°≈0,8,tan37°≈0.75, ≈1.7) 21·cn·jy·com
A.?102.5??????????????????????????????????????B.?87.5??????????????????????????????????????C.?85??????????????????????????????????????D.?70
13.为了方便学生在上下学期间安全过马路,南岸区政府决定在南开(融侨)中学校门口修建人行天桥(如图1),其平面图如图2所示,初三(8)班的学生小刘想利用所学知识测量天桥顶棚距地面的高度.天桥入口A点有一台阶AB=2m,其坡角为30°,在AB上方有两段平层BC=DE=1.5m,且BC,DE与地面平行,BC,DE上方又紧接台阶CD,EF,其长度相等且坡度均为i=4:3,顶棚距天桥距离FG=2m,且小刘从入口A点测得顶棚顶端G的仰角为37°,请根据以上数据,帮小刘计算出顶端G点距地面高度为(?? )m.(结果保留一位小数,参考数据: ≈1.73,sin37°≈ ,cos37°≈ ,tan37°≈ )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
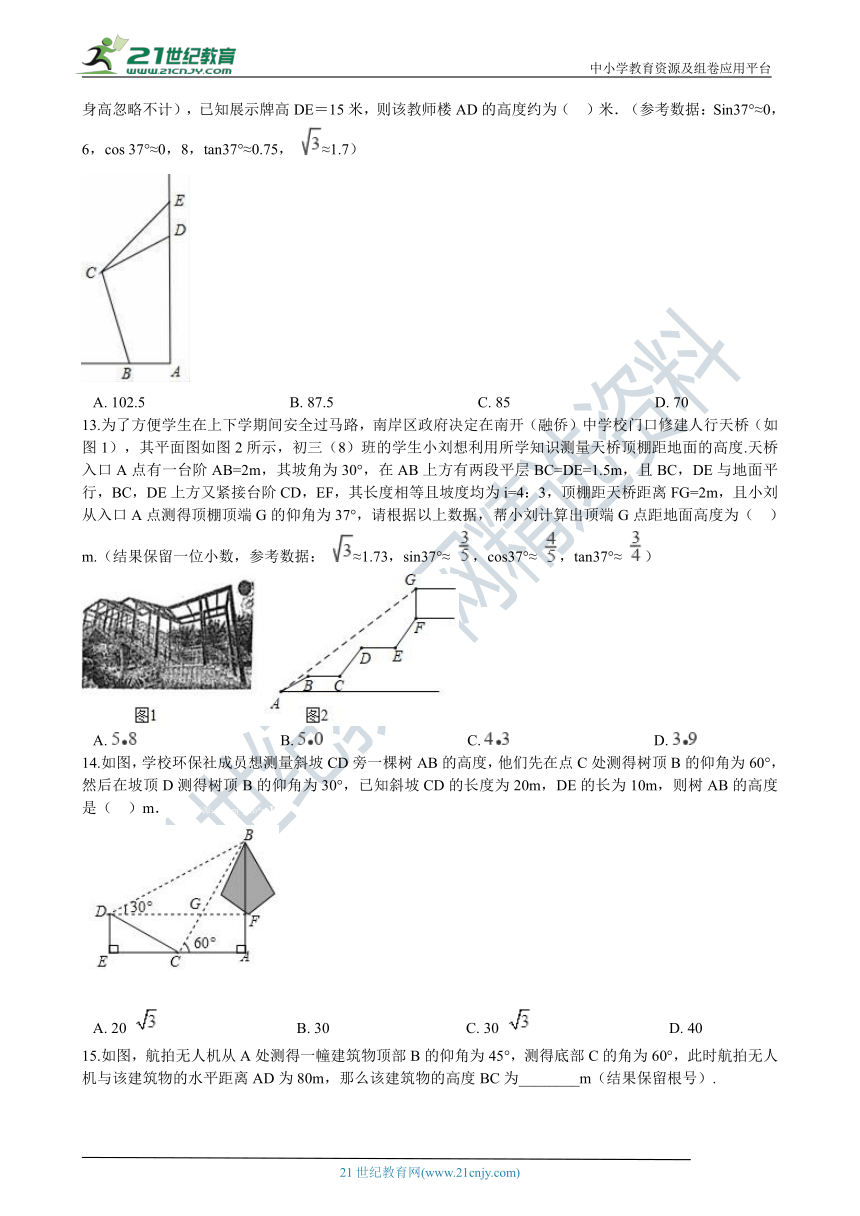
14.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是(?? )m. 【来源:21cnj*y.co*m】
A.?20 ????????????????????????????????????B.?30????????????????????????????????????C.?30 ????????????????????????????????????D.?40
15.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的角为60°,此时航拍无人机与该建筑物的水平距离AD为80m,那么该建筑物的高度BC为________m(结果保留根号).
16.如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为________米(结果保留根号).www.21-cn-jy.com
17.清泉阁是南宁园博园中的最高建筑.某数学兴趣小组利用周末到清泉阁进行室外测量实践活动.如图,在清泉阁最大的观景台上,选取测量点D,测得点D到清泉阁最高点A的仰角∠ADE=58°,点D到目标点C的俯角∠FDC=32°,DE=20m.已知清泉阁的高AB=75m,请计算测量点D到目标点C的距离(结果取整数).(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
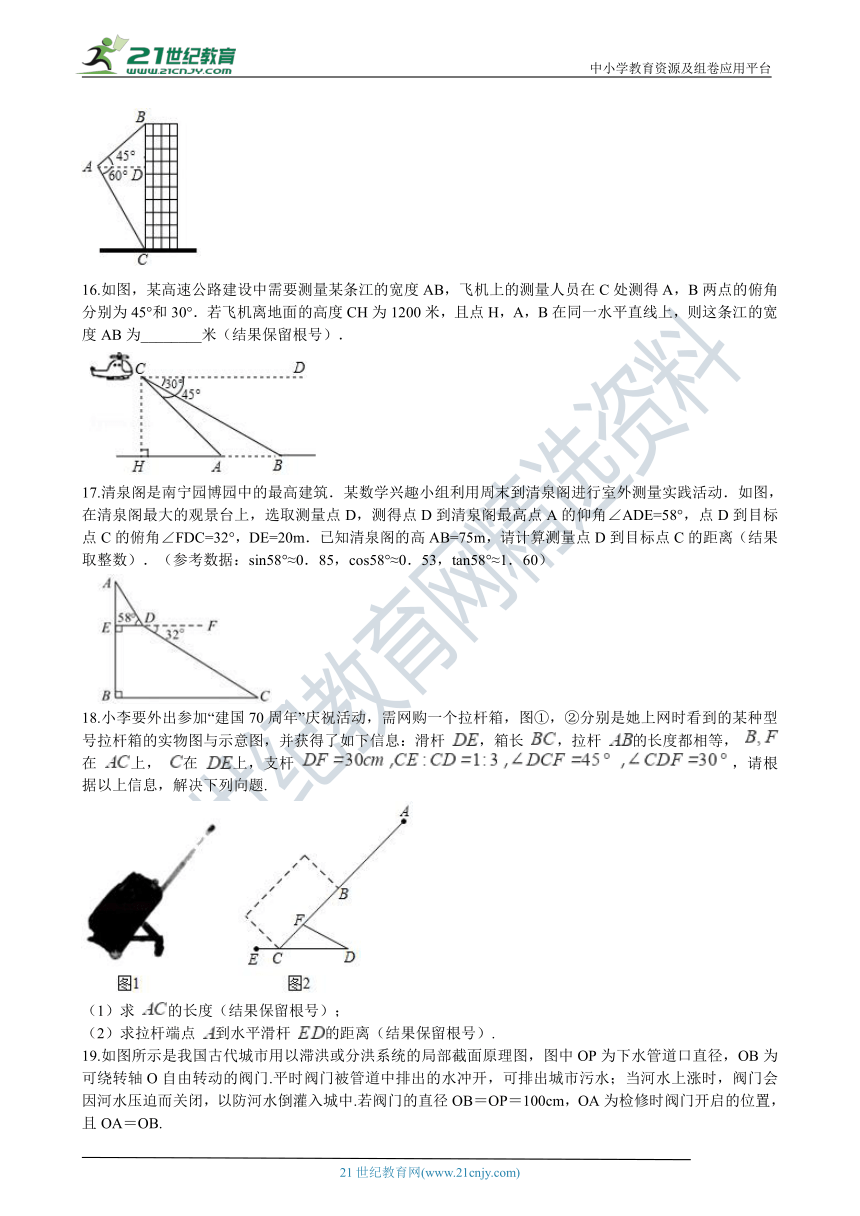
18.小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等, 在 上, 在 上,支杆 ,请根据以上信息,解决下列向题.
(1)求 的长度(结果保留根号);
(2)求拉杆端点 到水平滑杆 的距离(结果保留根号).
19.如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中OP为下水管道口直径,OB为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径OB=OP=100cm,OA为检修时阀门开启的位置,且OA=OB.
( =1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达OB位置时,在点A处测得俯角∠CAB=67.5°,若此时点B恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
答案解析部分
一、基础夯实
1. B
解:过点C作CE⊥BD于E,
∵∠BCE=45°,
∴△CEB是等腰直角三角形,
∴CE=BE=8,
四边形ACED是矩形,
∴AC=DE=1.6,
∴BD=8+1.6=9.6米,
故答案为:B.
【分析】过点C作CE⊥BD于E,很容易得出△CEB是等腰直角三角形,根据等腰直角三角形的性质得出CE=BE=8,也很容易判断出四边形ACED是矩形,根据矩形的性质得出AC=DE=1.6,从而根据线段的和差,由BD=DE+BE即可算出答案.
2. C
在Rt△ABD和Rt△ABC中,AB=a,tanα= ,tanβ= ,
∴BC=atanα,BD=atanβ,
∴CD=BC+BD=atanα+atanβ,
故答案为:C.
【分析】根据解直角三角形可求出BC、BD的长,由CD=BC+BD计算即得.
3. B
在Rt△ABD中,∵AB=m,∠BAD=β,
∴BD=AB?tanβ=mtanβ,
在Rt△ABC中,∵AB=m,∠BAC=α,
∴BC=AB?tanα=mtanα,
∴CD=BD﹣BC=mtanβ﹣mtanα,
故答案为:B。
【分析】在Rt△ABD中,根据正切函数的定义,由BD=AB?tanβ=mtanβ表示出BD,在Rt△ABC中,利用正切函数的定义,由BC=AB?tanα=mtanα,表示出BC,最后根据CD=BD﹣BC算出CD。
4. C
在Rt△ADE中,∵ tana= = =
∴DE=1.5,CD=CE+DE=1.7+1.5=3.2(米).
故答案为:C.
【分析】根据矩形的性质得出AE=BC,根据正切函数的定义由 tana= 即可求出ED的长,进而根据线段的和差即可算出答案。【来源:21·世纪·教育·网】
5. D
由题意得,∠B= ,
在Rt△ACB中,tanB= ,
则BC= 米,
故答案为:D.
【分析】根据两直线平行内错角相等,可得∠B= .在Rt△ACB中,由tanB= , 即可求出BC的值.
6. B
解:在Rt△ABD中,
∵∠ADB=45°,
∴BD=AB.
在Rt△ABC中,
∵∠ACB=30°,
∴BC= AB.
设AB=x(米),
∵CD=14,
∴BC=x+14.
∴x+14= x
∴x=7 +7.
即铁塔AB的高为(7 + 7)米.
故答案为:B.
【分析】根据等角对等边可得BD=AB,利用解直角三角形,可求出BC= AB,设AB=x(米),可得BC=x+14,即得等量x+14= x,解出x值即可.21*cnjy*com
7.
在 中, ,
则 ,
在 中, ,
∴ ,
∴ ,
故答案为: .
【分析】利用锐角三角函数的定义,在Rt△PBD中,求出BD的长,再在Rt△PBD中,去证明CD=PD,可得CD的长,然后由BC=BD-CD,从而可求出BC的长。www-2-1-cnjy-com
8.
解: 由题意可得:∠BDA=45°,
则AB=AD=120m,
又∵∠CAD=30°,
∴在Rt△ADC中,
tan∠CDA=tan30°= = ,
解得:CD=40 (m),
故答案为:40 .
【分析】在等腰直角三角形ABD中,AB=AD;在Rt△ADC中,根据tan∠CDA=tan30°= 计算即可求解。21教育名师原创作品
9. 解:设PQ=MN=xm,
在Rt△APQ中,tanA= ,
则AQ= ≈ =4x,
在Rt△MBN中,tan∠MBN= ,
则BN= ≈ = ,
∵AQ+QN=AB+BN,
∴4x+10=25+ ,
解得,x≈8.4,
答:路灯的高度约为8.4m。
【分析】 设PQ=MN=xm, 根据正切函数的定义,由 tanA= , tan∠MBN= , 分别表示出AQ,BN,进而根据 AQ+QN=AB+BN建立方程,求解即可.
10. (1)解:在Rt△GDF中,∵∠FGD=60°、GD=4,
∴DF=GDtan∠FGD=4 ,
在Rt△DEG中,∵∠EGD=45°,
∴GD=ED=4,
∴EF=DF﹣DE=4 ﹣4,
∴S矩形=5(4 ﹣4)=20 ﹣20(平方米),
答:灯牌的面积为(20 ﹣20)平方米。
(2)解:在Rt△GDF中,FG= =8,
在Rt△DEG中,GE= =4 ,
因此两侧加固的铝合金框架总共用料2(8+4 )=(16+8 )米.
【分析】(1) 在Rt△GDF中 ,利用解直角三角形求出DF的长.在Rt△DEG中,利用等角对等边可得 GD=ED=4,由EF=DF﹣DE求出EF的长,利用矩形的面积=长×宽计算即可. (2) 在Rt△GDF中,利用解直角三角形求出FG的长,在Rt△DEG中,利用解直角三角形求出GE的长,从而求出结论.
二、提高特训
11. C
解:过点 作 于点 ,延长 交 于点 ,
设 ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
故答案为:C.
【分析】过点 作 于点 ,延长 交 于点 ,设 ,根据正切函数的定义得出 ,, 根据用两个不同的式子表示同一个量,则这两个式子应该相等列出方程,求解算出x的值,从而即可根据OE=OF+EF即可算出答案.21*cnjy*com
12. B
解:作CF⊥AE于F,CG⊥AB于G,则四边形AFCG是矩形.
∵在Rt△BCG中,BC=50,斜坡BC的坡度i= :1
∴tan∠CBG= :1,
∴∠CBG=60°,∴∠BCG=30°,
∴BG= BC=25,CG=25 .
设DF=x.
∵在Rt△DCF中,∠DCF=45°,
∴CF=DF=x.
∵在Rt△ECF中,∠ECF=53°,
∴∠CEF=37°,
∵tan∠CEF= = ≈0.75,
∴x=45,∴DF=45
∴AD=AF+DF=25 +45≈87.5(米),
故答案为:B.
【分析】作CF⊥AE于F,CG⊥AB于G,则四边形AFCG是矩形,根据坡度的定义及锐角三角函数的定义,可求出BG、CG的长,设DF=x,则CF=x,利用解直角三角形求出DF的长,然后根据AD=DF+AF,就可求出AD的长。
13. C
如图,延长GF交过点A的水平线于J,作BH⊥AJ于H,CK⊥GJ于K,EM⊥GJ于M,DN⊥CK于K.
设CD=EF=5k,则FM=DN=4k,EM=CN=3k,BH= AB=1,AH= BH= ,
∴AJ= +1.5+1.5+6k= +3+6k,GJ=2+8k+1=3+8k,
∵tan37°= ,
∴ ,
∴k≈0.156,
∴GJ=3+8×0.156≈4.3(m),
故答案为:C.
【分析】如图,延长GF交过点A的水平线于J,作BH⊥AJ于H,CK⊥GJ于K,EM⊥GJ于M,DN⊥CK于K.设CD=EF=5k,则FM=DN=4k,EM=CN=3k,从而求出AJ= +3+6k,GJ=3+8k,根据30°角的直角三角形的性质求出BH、AH的长,由tan37°= ,即可求出k值,从而求出GJ的长.
14. B
解: 在Rt△CDE中,
∵CD=20m,DE=10m,
∴sin∠DCE= = ,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC= = =20 m,
∴AB=BC?sin60°=20 × =30m.
故答案为:B.
方法二:可以证明△DGC≌△BGF,所以BF=DC=20,所以AB=20+10=30,
故答案为:B.
【分析】在Rt△CDE中,sin∠DCE=, 由特殊角的三角函数值可得∠DCE的度数,结合已知条件易证∠ABC=30°,∠DCB=90°.在直角三角形BDC中,由锐角三角函数可得BC= , 则AB=BC?sin60°可求解。2-1-c-n-j-y
15. (80+80 )
解:∵在Rt△ABD中,AD=80,∠BAD=45°,
∴BD=AD=80(m),
∵在Rt△ACD中,∠CAD=60°,
∴CD=AD?tan60°=80× =80 (m),
∴BC=BD+CD=(80+80 )(m)
答:该建筑物的高度BC约为=(80+80 )米.
故答案为:(80+80 ).
【分析】在Rt△ABD中,根据等腰直角三角形的性质得出BD=AD=80(m),在Rt△ACD中,根据正切函数的定义及特殊锐角三角函数值,由CD=AD?tan60°算出CD,最后根据BC=BD+CD算出答案。
16.1200( ﹣1)
解: 由于CD∥HB,
∴∠CAH=∠ACD=45°,∠B=∠BCD=30°
在Rt△ACH中,∵∴∠CAH=45°
∴AH=CH=1200米,
在Rt△HCB,∵tan∠B=
∴HB= =
= =1200 (米).
∴AB=HB﹣HA
=1200 ﹣1200
=1200( ﹣1)米
故答案为:1200( ﹣1)
【分析】在等腰Rt△ACH中,AH=CH;在Rt△HCB,根据tan∠B= 可求得BH的值,则AB=HB﹣HA可求解。21世纪教育网版权所有
17. 解:过点D作DH⊥BC,垂足为H,
?∵在Rt△AED中,tan∠ADE=
∴AE=DE·tan58°≈20×1.60=32 m
∴EB=AB-AE=75-32=43 m
∵DH⊥BC,DE⊥AB,AB⊥BC
∴∠DEB=∠B=∠DHB=90°,
∴四边形BHDE是矩形,
∵DH=EB=43 m.
∵∠FDC=32°
∴∠CDH=90°-32=58°
∵在Rt△DCH中,cos∠CDH=
∴DC≈ ≈81m
答:测量点D到目标点C的距离约为81m
【分析】 过点D作DH⊥BC,垂足为H,在Rt△AED中,由 tan∠ADE=? , 可求出 AE =32 m , ?即得 EB=AB-AE=43 m.根据三个角是直角的四边形是矩形,可证四边形BHDE是矩形,利用矩形的性质可得DH=EB=43 m.利用角的和差可求出∠CDH=90°-∠FDC=58°, 在Rt△DCH中,由cos∠CDH=? , 可求出DC的长. 【出处:21教育名师】
18. (1)解:过 作 于 ,
(2)解:过 作 交 的延长线于 ,
答:拉杆端点 到水平滑杆 的距离为
【分析】(1) 过 作 于 , 根据含30°的直角三角形的边之间的关系得出
根据等腰直角三角形的性质得出CH=FH=15,进而根据线段的和差算出CD,又CE∶CD=1∶3,从而算出DE的长,然后根据AB=BC=DE,且AC=BC+AB即可算出答案; (2) 过 作 交 的延长线于 , 根据等腰直角三角形的性质即可得出
19. (1)解:阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围为:0°≤∠POB≤90° (2)解:如图, 21cnjy.com
∵∠CAB=67.5°,
∴∠BAO=22.5°,
∵OA=OB,
∴∠BAO=∠ABO=22.5°,
∴∠BOP=45°,
∵OB=100,
∴OE= OB=50 ,
∴PE=OP﹣OE=100﹣50 ≈29.5cm,
答:此时下水道内水的深度约为29.5cm.
【分析】(1)根据题意 阀门被下水道的水冲开 的最大位置是OB⊥OA, 被河水关闭过程中最大位置就是AOB三点在同一直线上,从而即可得出答案; (2)根据角的和差及等边对等角得出 ∠BAO=∠ABO=22.5°, 根据三角形的外角定理得出 ∠BOP=45°, 根据等腰直角三角形的性质得出 OE= OB=50 , 进而根据 PE=OP﹣OE 即可算出答案。
一、基础夯实
1.如图,护林员在离树8m的A处测得树顶B的仰角为45°,已知护林员的眼睛离地面的距离AC为1.6m,则树的高度BD为(?? ) 21教育网
A.?8m???????????????????????????B.?9.6m???????????????????????????C.?(4 +1.6)m???????????????????????????D.?(8 +1.6)m
2.南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为(???? ) 2·1·c·n·j·y
A.?asinα+asinβ??????????????????B.?acosα+acosβ??????????????????C.?atanα+atanβ??????????????????D.?
3.如图,某同学在距离建筑中心B点m米的点A处,测得旗杆底部点C的仰角为α,旗杆顶部点D的仰角为β,则旗杆CD的长为( ??) 21·世纪*教育网
A.?????????????????B.?mtanβ﹣mtanα????????????????C.?????????????????D.?msinβ﹣msinα
4.小明在某次投篮中刚好把球打到篮板的点D处后进球,已知小明与篮框底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为∠α,已知tanα= ,则点D到地面的距离CD是(?? )
A.?2.7米???????????????????????????????????B.?3.0米???????????????????????????????????C.?3.2米???????????????????????????????????D.?3.4米
5.如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升200米到达A处,在A处观察B地的俯角为α,则B,C两地之间的距离为(?? ) 【版权所有:21教育】
A.?米?????????????????????????B.?米?????????????????????????C.?米?????????????????????????D.?米
6.如图,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14m到达D,在D处测得A的仰角为45°,塔高AB为(?? )
A.?(16 -4) m??????????????????B.?(7 +7) m??????????????????C.?(16 +7) m??????????????????D.?(10 +7) m
7.如图,在 处利用测角仪测得某建筑物 的顶端 点的仰角为60°,点 的仰角为45°,点 到建筑物的距离为 米,则 ________米.
8.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是________m(结果保留根号)
9.如图,在某街道路边有相距10m、高度相同的两盏路灯(灯杆垂直地面),小明为了测量路灯的高度,在地面A处测得路灯PQ的顶端仰角为14°,向前行走25m到达B处,在地面测得路灯MN的顶端仰角为24.3°,已知点A,B,Q,N在同一条直线上,请你利用所学知识帮助小明求出路灯的高度.(结果精确到0.1m.参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,sin24.3°≈0.41,cos24.3°≈0.91,tan24.3°≈0.45)
10.某居民小区物业要在广场树立一个“扫黑除恶,共创和谐”的矩形电子灯牌,如图所示,施工人员在两侧加固合金框架,已知合金框架底端G距广告牌立柱FD的距离GD=4米,从G点测得广告牌顶端F点和底端E点的仰角分别是60°和45°.
(1)若AF长为5米,求灯牌的面积;
(2)求两侧加固的铝合金框架总共用料多少米?(本题中的计算过程和结果均保留根号)
二、提高特训
11.小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高 为1.5米,她先站在 处看路灯顶端 的仰角为 ,再往前走3米站在 处,看路灯顶端 的仰角为 ,则路灯顶端 到地面的距离约为(已知 , , )(?? )
A.?米????????????????????????????????B.?米????????????????????????????????C.?米????????????????????????????????D.?米
12.如图,我校本部教师楼AD上有“育才中学”四个字的展示牌DE,某数学兴趣小组的同学准备利用所学的三角函数知识估测该教师楼的高度,由于场地有限,不便测量,所以小明沿坡度i= :1的阶梯从看台前的B处前行50米到达C处,测得展示牌底部D的仰角为45°,展示牌顶部E的仰角为53°(小明的身高忽略不计),已知展示牌高DE=15米,则该教师楼AD的高度约为(?? )米.(参考数据:Sin37°≈0,6,cos 37°≈0,8,tan37°≈0.75, ≈1.7) 21·cn·jy·com
A.?102.5??????????????????????????????????????B.?87.5??????????????????????????????????????C.?85??????????????????????????????????????D.?70
13.为了方便学生在上下学期间安全过马路,南岸区政府决定在南开(融侨)中学校门口修建人行天桥(如图1),其平面图如图2所示,初三(8)班的学生小刘想利用所学知识测量天桥顶棚距地面的高度.天桥入口A点有一台阶AB=2m,其坡角为30°,在AB上方有两段平层BC=DE=1.5m,且BC,DE与地面平行,BC,DE上方又紧接台阶CD,EF,其长度相等且坡度均为i=4:3,顶棚距天桥距离FG=2m,且小刘从入口A点测得顶棚顶端G的仰角为37°,请根据以上数据,帮小刘计算出顶端G点距地面高度为(?? )m.(结果保留一位小数,参考数据: ≈1.73,sin37°≈ ,cos37°≈ ,tan37°≈ )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
14.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是(?? )m. 【来源:21cnj*y.co*m】
A.?20 ????????????????????????????????????B.?30????????????????????????????????????C.?30 ????????????????????????????????????D.?40
15.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的角为60°,此时航拍无人机与该建筑物的水平距离AD为80m,那么该建筑物的高度BC为________m(结果保留根号).
16.如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为________米(结果保留根号).www.21-cn-jy.com
17.清泉阁是南宁园博园中的最高建筑.某数学兴趣小组利用周末到清泉阁进行室外测量实践活动.如图,在清泉阁最大的观景台上,选取测量点D,测得点D到清泉阁最高点A的仰角∠ADE=58°,点D到目标点C的俯角∠FDC=32°,DE=20m.已知清泉阁的高AB=75m,请计算测量点D到目标点C的距离(结果取整数).(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
18.小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等, 在 上, 在 上,支杆 ,请根据以上信息,解决下列向题.
(1)求 的长度(结果保留根号);
(2)求拉杆端点 到水平滑杆 的距离(结果保留根号).
19.如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中OP为下水管道口直径,OB为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径OB=OP=100cm,OA为检修时阀门开启的位置,且OA=OB.
( =1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达OB位置时,在点A处测得俯角∠CAB=67.5°,若此时点B恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
答案解析部分
一、基础夯实
1. B
解:过点C作CE⊥BD于E,
∵∠BCE=45°,
∴△CEB是等腰直角三角形,
∴CE=BE=8,
四边形ACED是矩形,
∴AC=DE=1.6,
∴BD=8+1.6=9.6米,
故答案为:B.
【分析】过点C作CE⊥BD于E,很容易得出△CEB是等腰直角三角形,根据等腰直角三角形的性质得出CE=BE=8,也很容易判断出四边形ACED是矩形,根据矩形的性质得出AC=DE=1.6,从而根据线段的和差,由BD=DE+BE即可算出答案.
2. C
在Rt△ABD和Rt△ABC中,AB=a,tanα= ,tanβ= ,
∴BC=atanα,BD=atanβ,
∴CD=BC+BD=atanα+atanβ,
故答案为:C.
【分析】根据解直角三角形可求出BC、BD的长,由CD=BC+BD计算即得.
3. B
在Rt△ABD中,∵AB=m,∠BAD=β,
∴BD=AB?tanβ=mtanβ,
在Rt△ABC中,∵AB=m,∠BAC=α,
∴BC=AB?tanα=mtanα,
∴CD=BD﹣BC=mtanβ﹣mtanα,
故答案为:B。
【分析】在Rt△ABD中,根据正切函数的定义,由BD=AB?tanβ=mtanβ表示出BD,在Rt△ABC中,利用正切函数的定义,由BC=AB?tanα=mtanα,表示出BC,最后根据CD=BD﹣BC算出CD。
4. C
在Rt△ADE中,∵ tana= = =
∴DE=1.5,CD=CE+DE=1.7+1.5=3.2(米).
故答案为:C.
【分析】根据矩形的性质得出AE=BC,根据正切函数的定义由 tana= 即可求出ED的长,进而根据线段的和差即可算出答案。【来源:21·世纪·教育·网】
5. D
由题意得,∠B= ,
在Rt△ACB中,tanB= ,
则BC= 米,
故答案为:D.
【分析】根据两直线平行内错角相等,可得∠B= .在Rt△ACB中,由tanB= , 即可求出BC的值.
6. B
解:在Rt△ABD中,
∵∠ADB=45°,
∴BD=AB.
在Rt△ABC中,
∵∠ACB=30°,
∴BC= AB.
设AB=x(米),
∵CD=14,
∴BC=x+14.
∴x+14= x
∴x=7 +7.
即铁塔AB的高为(7 + 7)米.
故答案为:B.
【分析】根据等角对等边可得BD=AB,利用解直角三角形,可求出BC= AB,设AB=x(米),可得BC=x+14,即得等量x+14= x,解出x值即可.21*cnjy*com
7.
在 中, ,
则 ,
在 中, ,
∴ ,
∴ ,
故答案为: .
【分析】利用锐角三角函数的定义,在Rt△PBD中,求出BD的长,再在Rt△PBD中,去证明CD=PD,可得CD的长,然后由BC=BD-CD,从而可求出BC的长。www-2-1-cnjy-com
8.
解: 由题意可得:∠BDA=45°,
则AB=AD=120m,
又∵∠CAD=30°,
∴在Rt△ADC中,
tan∠CDA=tan30°= = ,
解得:CD=40 (m),
故答案为:40 .
【分析】在等腰直角三角形ABD中,AB=AD;在Rt△ADC中,根据tan∠CDA=tan30°= 计算即可求解。21教育名师原创作品
9. 解:设PQ=MN=xm,
在Rt△APQ中,tanA= ,
则AQ= ≈ =4x,
在Rt△MBN中,tan∠MBN= ,
则BN= ≈ = ,
∵AQ+QN=AB+BN,
∴4x+10=25+ ,
解得,x≈8.4,
答:路灯的高度约为8.4m。
【分析】 设PQ=MN=xm, 根据正切函数的定义,由 tanA= , tan∠MBN= , 分别表示出AQ,BN,进而根据 AQ+QN=AB+BN建立方程,求解即可.
10. (1)解:在Rt△GDF中,∵∠FGD=60°、GD=4,
∴DF=GDtan∠FGD=4 ,
在Rt△DEG中,∵∠EGD=45°,
∴GD=ED=4,
∴EF=DF﹣DE=4 ﹣4,
∴S矩形=5(4 ﹣4)=20 ﹣20(平方米),
答:灯牌的面积为(20 ﹣20)平方米。
(2)解:在Rt△GDF中,FG= =8,
在Rt△DEG中,GE= =4 ,
因此两侧加固的铝合金框架总共用料2(8+4 )=(16+8 )米.
【分析】(1) 在Rt△GDF中 ,利用解直角三角形求出DF的长.在Rt△DEG中,利用等角对等边可得 GD=ED=4,由EF=DF﹣DE求出EF的长,利用矩形的面积=长×宽计算即可. (2) 在Rt△GDF中,利用解直角三角形求出FG的长,在Rt△DEG中,利用解直角三角形求出GE的长,从而求出结论.
二、提高特训
11. C
解:过点 作 于点 ,延长 交 于点 ,
设 ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
故答案为:C.
【分析】过点 作 于点 ,延长 交 于点 ,设 ,根据正切函数的定义得出 ,, 根据用两个不同的式子表示同一个量,则这两个式子应该相等列出方程,求解算出x的值,从而即可根据OE=OF+EF即可算出答案.21*cnjy*com
12. B
解:作CF⊥AE于F,CG⊥AB于G,则四边形AFCG是矩形.
∵在Rt△BCG中,BC=50,斜坡BC的坡度i= :1
∴tan∠CBG= :1,
∴∠CBG=60°,∴∠BCG=30°,
∴BG= BC=25,CG=25 .
设DF=x.
∵在Rt△DCF中,∠DCF=45°,
∴CF=DF=x.
∵在Rt△ECF中,∠ECF=53°,
∴∠CEF=37°,
∵tan∠CEF= = ≈0.75,
∴x=45,∴DF=45
∴AD=AF+DF=25 +45≈87.5(米),
故答案为:B.
【分析】作CF⊥AE于F,CG⊥AB于G,则四边形AFCG是矩形,根据坡度的定义及锐角三角函数的定义,可求出BG、CG的长,设DF=x,则CF=x,利用解直角三角形求出DF的长,然后根据AD=DF+AF,就可求出AD的长。
13. C
如图,延长GF交过点A的水平线于J,作BH⊥AJ于H,CK⊥GJ于K,EM⊥GJ于M,DN⊥CK于K.
设CD=EF=5k,则FM=DN=4k,EM=CN=3k,BH= AB=1,AH= BH= ,
∴AJ= +1.5+1.5+6k= +3+6k,GJ=2+8k+1=3+8k,
∵tan37°= ,
∴ ,
∴k≈0.156,
∴GJ=3+8×0.156≈4.3(m),
故答案为:C.
【分析】如图,延长GF交过点A的水平线于J,作BH⊥AJ于H,CK⊥GJ于K,EM⊥GJ于M,DN⊥CK于K.设CD=EF=5k,则FM=DN=4k,EM=CN=3k,从而求出AJ= +3+6k,GJ=3+8k,根据30°角的直角三角形的性质求出BH、AH的长,由tan37°= ,即可求出k值,从而求出GJ的长.
14. B
解: 在Rt△CDE中,
∵CD=20m,DE=10m,
∴sin∠DCE= = ,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC= = =20 m,
∴AB=BC?sin60°=20 × =30m.
故答案为:B.
方法二:可以证明△DGC≌△BGF,所以BF=DC=20,所以AB=20+10=30,
故答案为:B.
【分析】在Rt△CDE中,sin∠DCE=, 由特殊角的三角函数值可得∠DCE的度数,结合已知条件易证∠ABC=30°,∠DCB=90°.在直角三角形BDC中,由锐角三角函数可得BC= , 则AB=BC?sin60°可求解。2-1-c-n-j-y
15. (80+80 )
解:∵在Rt△ABD中,AD=80,∠BAD=45°,
∴BD=AD=80(m),
∵在Rt△ACD中,∠CAD=60°,
∴CD=AD?tan60°=80× =80 (m),
∴BC=BD+CD=(80+80 )(m)
答:该建筑物的高度BC约为=(80+80 )米.
故答案为:(80+80 ).
【分析】在Rt△ABD中,根据等腰直角三角形的性质得出BD=AD=80(m),在Rt△ACD中,根据正切函数的定义及特殊锐角三角函数值,由CD=AD?tan60°算出CD,最后根据BC=BD+CD算出答案。
16.1200( ﹣1)
解: 由于CD∥HB,
∴∠CAH=∠ACD=45°,∠B=∠BCD=30°
在Rt△ACH中,∵∴∠CAH=45°
∴AH=CH=1200米,
在Rt△HCB,∵tan∠B=
∴HB= =
= =1200 (米).
∴AB=HB﹣HA
=1200 ﹣1200
=1200( ﹣1)米
故答案为:1200( ﹣1)
【分析】在等腰Rt△ACH中,AH=CH;在Rt△HCB,根据tan∠B= 可求得BH的值,则AB=HB﹣HA可求解。21世纪教育网版权所有
17. 解:过点D作DH⊥BC,垂足为H,
?∵在Rt△AED中,tan∠ADE=
∴AE=DE·tan58°≈20×1.60=32 m
∴EB=AB-AE=75-32=43 m
∵DH⊥BC,DE⊥AB,AB⊥BC
∴∠DEB=∠B=∠DHB=90°,
∴四边形BHDE是矩形,
∵DH=EB=43 m.
∵∠FDC=32°
∴∠CDH=90°-32=58°
∵在Rt△DCH中,cos∠CDH=
∴DC≈ ≈81m
答:测量点D到目标点C的距离约为81m
【分析】 过点D作DH⊥BC,垂足为H,在Rt△AED中,由 tan∠ADE=? , 可求出 AE =32 m , ?即得 EB=AB-AE=43 m.根据三个角是直角的四边形是矩形,可证四边形BHDE是矩形,利用矩形的性质可得DH=EB=43 m.利用角的和差可求出∠CDH=90°-∠FDC=58°, 在Rt△DCH中,由cos∠CDH=? , 可求出DC的长. 【出处:21教育名师】
18. (1)解:过 作 于 ,
(2)解:过 作 交 的延长线于 ,
答:拉杆端点 到水平滑杆 的距离为
【分析】(1) 过 作 于 , 根据含30°的直角三角形的边之间的关系得出
根据等腰直角三角形的性质得出CH=FH=15,进而根据线段的和差算出CD,又CE∶CD=1∶3,从而算出DE的长,然后根据AB=BC=DE,且AC=BC+AB即可算出答案; (2) 过 作 交 的延长线于 , 根据等腰直角三角形的性质即可得出
19. (1)解:阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围为:0°≤∠POB≤90° (2)解:如图, 21cnjy.com
∵∠CAB=67.5°,
∴∠BAO=22.5°,
∵OA=OB,
∴∠BAO=∠ABO=22.5°,
∴∠BOP=45°,
∵OB=100,
∴OE= OB=50 ,
∴PE=OP﹣OE=100﹣50 ≈29.5cm,
答:此时下水道内水的深度约为29.5cm.
【分析】(1)根据题意 阀门被下水道的水冲开 的最大位置是OB⊥OA, 被河水关闭过程中最大位置就是AOB三点在同一直线上,从而即可得出答案; (2)根据角的和差及等边对等角得出 ∠BAO=∠ABO=22.5°, 根据三角形的外角定理得出 ∠BOP=45°, 根据等腰直角三角形的性质得出 OE= OB=50 , 进而根据 PE=OP﹣OE 即可算出答案。
