浙教版九年级数学上册第3章 圆的基本性质3.1 圆 确定圆的条件——外接圆(含答案)
文档属性
| 名称 | 浙教版九年级数学上册第3章 圆的基本性质3.1 圆 确定圆的条件——外接圆(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 259.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 23:02:58 | ||
图片预览

文档简介
确定圆的条件——外接圆
1.如图△ABC中外接圆的圆心坐标是______.
2.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是______.
3.如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为______.
4.某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)
5.已知:如图,在四边形ABCD中,∠B=∠D=90°.求证:四边形ABCD有外接圆.
6.如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上.
(1)在图上标出△ABC的外接圆的圆心O.
(2)△ABC的外接圆的面积是______.
7.如图,点A、B、C是⊙0上的三点,B0平分∠ABC.求证:BA=BC.
8.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
9.如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB.
10.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
11.已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
12.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是______.
13.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为______cm.
14.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是______.
答案解析
1.如图△ABC中外接圆的圆心坐标是 (6,2) .
【考点】确定圆的条件;坐标与图形性质.菁优网版权所有
【分析】本题可借助网格在网格中根据三角形三边的位置作出它们的垂直平分线,垂直平分线相交于一点,该点就是圆心,根据网格中的单位长度即可求解.
【解答】解:分别做三角形的三边的垂直平分线,可知相交于点(6,2),
即△ABC中外接圆的圆心坐标是(6,2).
故答案为:(6,2).
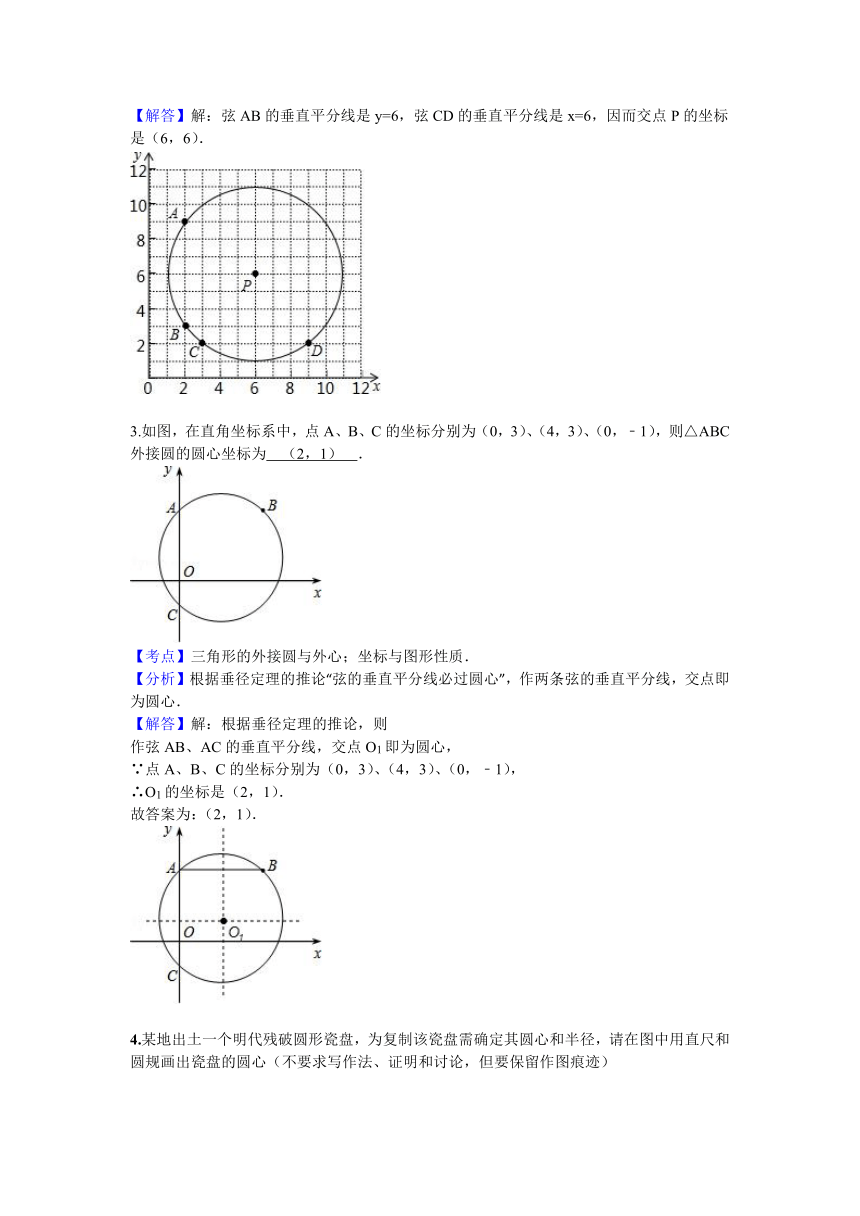
2.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是 (6,6) .
【考点】确定圆的条件;坐标与图形性质.菁优网版权所有
【分析】点P的坐标是弦AB,CD的垂直平分线的交点.
【解答】解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,因而交点P的坐标是(6,6).
3.如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为 (2,1) .
【考点】三角形的外接圆与外心;坐标与图形性质.菁优网版权所有
【分析】根据垂径定理的推论“弦的垂直平分线必过圆心”,作两条弦的垂直平分线,交点即为圆心.
【解答】解:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点O1即为圆心,
∵点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),
∴O1的坐标是(2,1).
故答案为:(2,1).
4.某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)
【考点】确定圆的条件.菁优网版权所有
【分析】根据垂径定理,在残破的圆形瓷盘上任取两个弦,分别作弦的垂直平分线即可.
【解答】解:在圆上取两个弦,根据垂径定理,
垂直平分弦的直线一定过圆心,
所以作出两弦的垂直平分线即可.
5.已知:如图,在四边形ABCD中,∠B=∠D=90°.求证:四边形ABCD有外接圆.
【考点】三角形的外接圆与外心.菁优网版权所有
【分析】根据直角三角形的斜边是其外接圆的直径,可得A,B,C,D都在以AC为直径的圆上.
【解答】证明:∵∠ABC=90°,
∴AC是△ABC的外接圆⊙O的直径,
而∠ADC=90°,
∴点D在⊙O上,
即四边形ABCD有外接圆.
6.如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上.
(1)在图上标出△ABC的外接圆的圆心O.
(2)△ABC的外接圆的面积是 10π .
【考点】三角形的外接圆与外心.菁优网版权所有
【分析】(1)根据三角形外心的确定方法得出O点位置即可;
(2)利用勾股定理得出AO的长,再利用圆的面积公式得出即可.
【解答】 解:(1)在图上标出 的外接圆的圆心O;
(2)∵AO==,
∴外接圆的面积是10π.
故答案为:10π.
7.如图,点A、B、C是⊙0上的三点,B0平分∠ABC.求证:BA=BC.
【考点】圆的认识;全等三角形的判定与性质.菁优网版权所有
【分析】连OA、OC,利用半径都相等得到OA=OB,OB=OC,根据等腰三角形的性质有∠ABO=∠BAO,∠CBO=∠BCO,而B0平分∠ABC,则∠ABO=∠CBO,根据三角形全等的判定得到△OAB≌△OCB,即可得到结论.
【解答】证明:连OA、OC,如图,
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO,
∵B0平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO,
∴△OAB≌△OCB,
∴AB=BC.
8.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
【考点】圆的认识;全等三角形的判定与性质.菁优网版权所有
【分析】根据AB、CD为⊙O中两条直径,得出OA=OB,OC=OD,再根据CE=DF,得出OE=OF,从而证出△AOF和△BOE全等,即可得出答案.
【解答】解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
9.如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB.
【考点】三角形的外接圆与外心.菁优网版权所有
【分析】利用三角形中线的性质以及等边三角形的判定方法得出△BDC是等边三角形,进而得出∠ACB=90°,求出BC=AB,即可得出答案.
【解答】证明:∵CD是△ABC的中线,AB=2CD,
∴AD=BD=CD,
∵∠B=60°,
∴△CDB是等边三角形,
∴∠BDC=∠DCB=60°,
∴∠A=∠ACD=30°,
∴∠ACB=90°,
∴AB是△ABC的外接圆的直径,
∵∠A=30°,∠ACB=90°,
∴BC=AB,
∴△ABC的外接圆的半径为CB.
10.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
【考点】圆的认识;等腰三角形的性质.菁优网版权所有
【分析】连接OD,如图,由AB=2DE,AB=2OD得到OD=DE,根据等腰三角形的性质得∠DOE=∠E=20°,再利用三角形外角性质得到∠CDO=40°,加上∠C=∠ODC=40°,然后再利用三角形外角性质即可计算出∠AOC.
【解答】解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
11.已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
【考点】点与圆的位置关系.菁优网版权所有
【分析】点P应分为位于圆的内部位于外部两种情况讨论.当点P在圆内时,点到圆的最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
【解答】解:如图,分为两种情况:
①当点P在圆内时,最近点的距离为7,最大距离为11,则直径是18,因而半径是9;
②当点P在圆外时,最近点的距离为7,最大距离为11,则直径是4,因而半径是2.
故此圆的半径为2或9.
12.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是 10 .
【考点】圆的认识;勾股定理.菁优网版权所有
【分析】先连接OC,在Rt△ODC中,根据勾股定理得出OC的长,即可求出AB的长.
【解答】解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC===5,
∴AB=2OC=10,
故答案为:10.
13.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为 4 cm.
【考点】圆的认识;等边三角形的判定与性质.菁优网版权所有
【分析】利用半径相等可判断△OAB为等边三角形,然后根据等边三角形的性质易得AB=4cm.
【解答】解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
14.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 3<r<5 .
【考点】点与圆的位置关系.菁优网版权所有
【分析】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
由图可知3<r<5.
1.如图△ABC中外接圆的圆心坐标是______.
2.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是______.
3.如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为______.
4.某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)
5.已知:如图,在四边形ABCD中,∠B=∠D=90°.求证:四边形ABCD有外接圆.
6.如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上.
(1)在图上标出△ABC的外接圆的圆心O.
(2)△ABC的外接圆的面积是______.
7.如图,点A、B、C是⊙0上的三点,B0平分∠ABC.求证:BA=BC.
8.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
9.如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB.
10.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
11.已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
12.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是______.
13.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为______cm.
14.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是______.
答案解析
1.如图△ABC中外接圆的圆心坐标是 (6,2) .
【考点】确定圆的条件;坐标与图形性质.菁优网版权所有
【分析】本题可借助网格在网格中根据三角形三边的位置作出它们的垂直平分线,垂直平分线相交于一点,该点就是圆心,根据网格中的单位长度即可求解.
【解答】解:分别做三角形的三边的垂直平分线,可知相交于点(6,2),
即△ABC中外接圆的圆心坐标是(6,2).
故答案为:(6,2).
2.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是 (6,6) .
【考点】确定圆的条件;坐标与图形性质.菁优网版权所有
【分析】点P的坐标是弦AB,CD的垂直平分线的交点.
【解答】解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,因而交点P的坐标是(6,6).
3.如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为 (2,1) .
【考点】三角形的外接圆与外心;坐标与图形性质.菁优网版权所有
【分析】根据垂径定理的推论“弦的垂直平分线必过圆心”,作两条弦的垂直平分线,交点即为圆心.
【解答】解:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点O1即为圆心,
∵点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),
∴O1的坐标是(2,1).
故答案为:(2,1).
4.某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)
【考点】确定圆的条件.菁优网版权所有
【分析】根据垂径定理,在残破的圆形瓷盘上任取两个弦,分别作弦的垂直平分线即可.
【解答】解:在圆上取两个弦,根据垂径定理,
垂直平分弦的直线一定过圆心,
所以作出两弦的垂直平分线即可.
5.已知:如图,在四边形ABCD中,∠B=∠D=90°.求证:四边形ABCD有外接圆.
【考点】三角形的外接圆与外心.菁优网版权所有
【分析】根据直角三角形的斜边是其外接圆的直径,可得A,B,C,D都在以AC为直径的圆上.
【解答】证明:∵∠ABC=90°,
∴AC是△ABC的外接圆⊙O的直径,
而∠ADC=90°,
∴点D在⊙O上,
即四边形ABCD有外接圆.
6.如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上.
(1)在图上标出△ABC的外接圆的圆心O.
(2)△ABC的外接圆的面积是 10π .
【考点】三角形的外接圆与外心.菁优网版权所有
【分析】(1)根据三角形外心的确定方法得出O点位置即可;
(2)利用勾股定理得出AO的长,再利用圆的面积公式得出即可.
【解答】 解:(1)在图上标出 的外接圆的圆心O;
(2)∵AO==,
∴外接圆的面积是10π.
故答案为:10π.
7.如图,点A、B、C是⊙0上的三点,B0平分∠ABC.求证:BA=BC.
【考点】圆的认识;全等三角形的判定与性质.菁优网版权所有
【分析】连OA、OC,利用半径都相等得到OA=OB,OB=OC,根据等腰三角形的性质有∠ABO=∠BAO,∠CBO=∠BCO,而B0平分∠ABC,则∠ABO=∠CBO,根据三角形全等的判定得到△OAB≌△OCB,即可得到结论.
【解答】证明:连OA、OC,如图,
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO,
∵B0平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO,
∴△OAB≌△OCB,
∴AB=BC.
8.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
【考点】圆的认识;全等三角形的判定与性质.菁优网版权所有
【分析】根据AB、CD为⊙O中两条直径,得出OA=OB,OC=OD,再根据CE=DF,得出OE=OF,从而证出△AOF和△BOE全等,即可得出答案.
【解答】解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
9.如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB.
【考点】三角形的外接圆与外心.菁优网版权所有
【分析】利用三角形中线的性质以及等边三角形的判定方法得出△BDC是等边三角形,进而得出∠ACB=90°,求出BC=AB,即可得出答案.
【解答】证明:∵CD是△ABC的中线,AB=2CD,
∴AD=BD=CD,
∵∠B=60°,
∴△CDB是等边三角形,
∴∠BDC=∠DCB=60°,
∴∠A=∠ACD=30°,
∴∠ACB=90°,
∴AB是△ABC的外接圆的直径,
∵∠A=30°,∠ACB=90°,
∴BC=AB,
∴△ABC的外接圆的半径为CB.
10.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
【考点】圆的认识;等腰三角形的性质.菁优网版权所有
【分析】连接OD,如图,由AB=2DE,AB=2OD得到OD=DE,根据等腰三角形的性质得∠DOE=∠E=20°,再利用三角形外角性质得到∠CDO=40°,加上∠C=∠ODC=40°,然后再利用三角形外角性质即可计算出∠AOC.
【解答】解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
11.已知点P到圆的最大距离为11,最小距离为7,则此圆的半径为多少?(要求作图解答)
【考点】点与圆的位置关系.菁优网版权所有
【分析】点P应分为位于圆的内部位于外部两种情况讨论.当点P在圆内时,点到圆的最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
【解答】解:如图,分为两种情况:
①当点P在圆内时,最近点的距离为7,最大距离为11,则直径是18,因而半径是9;
②当点P在圆外时,最近点的距离为7,最大距离为11,则直径是4,因而半径是2.
故此圆的半径为2或9.
12.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是 10 .
【考点】圆的认识;勾股定理.菁优网版权所有
【分析】先连接OC,在Rt△ODC中,根据勾股定理得出OC的长,即可求出AB的长.
【解答】解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC===5,
∴AB=2OC=10,
故答案为:10.
13.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为 4 cm.
【考点】圆的认识;等边三角形的判定与性质.菁优网版权所有
【分析】利用半径相等可判断△OAB为等边三角形,然后根据等边三角形的性质易得AB=4cm.
【解答】解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
14.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 3<r<5 .
【考点】点与圆的位置关系.菁优网版权所有
【分析】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
由图可知3<r<5.
同课章节目录
