浙教版九年级数学下册 第二章 直线与圆的位置关系 期末专题复习检测试卷(有答案)
文档属性
| 名称 | 浙教版九年级数学下册 第二章 直线与圆的位置关系 期末专题复习检测试卷(有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 189.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 00:00:00 | ||
图片预览


文档简介
期末专题复习:浙教版九年级数学下册 第二章 直线与圆的位置关系 单元检测试卷
一、单选题(共10题;共30分)
1.到三角形三边距离都相等的点是三角形(???)的交点
A.?三边中垂线????????????????????????B.?三条中线????????????????????????C.?三条高????????????????????????D.?三条内角平分线
2.已知直线l与半径为r的☉O相交,且点O到直线l的距离为6,则r的取值范围是(?? )
A.?r<6??????????????????????????????????????B.?r=6??????????????????????????????????????C.?r>6??????????????????????????????????????D.?r≥6
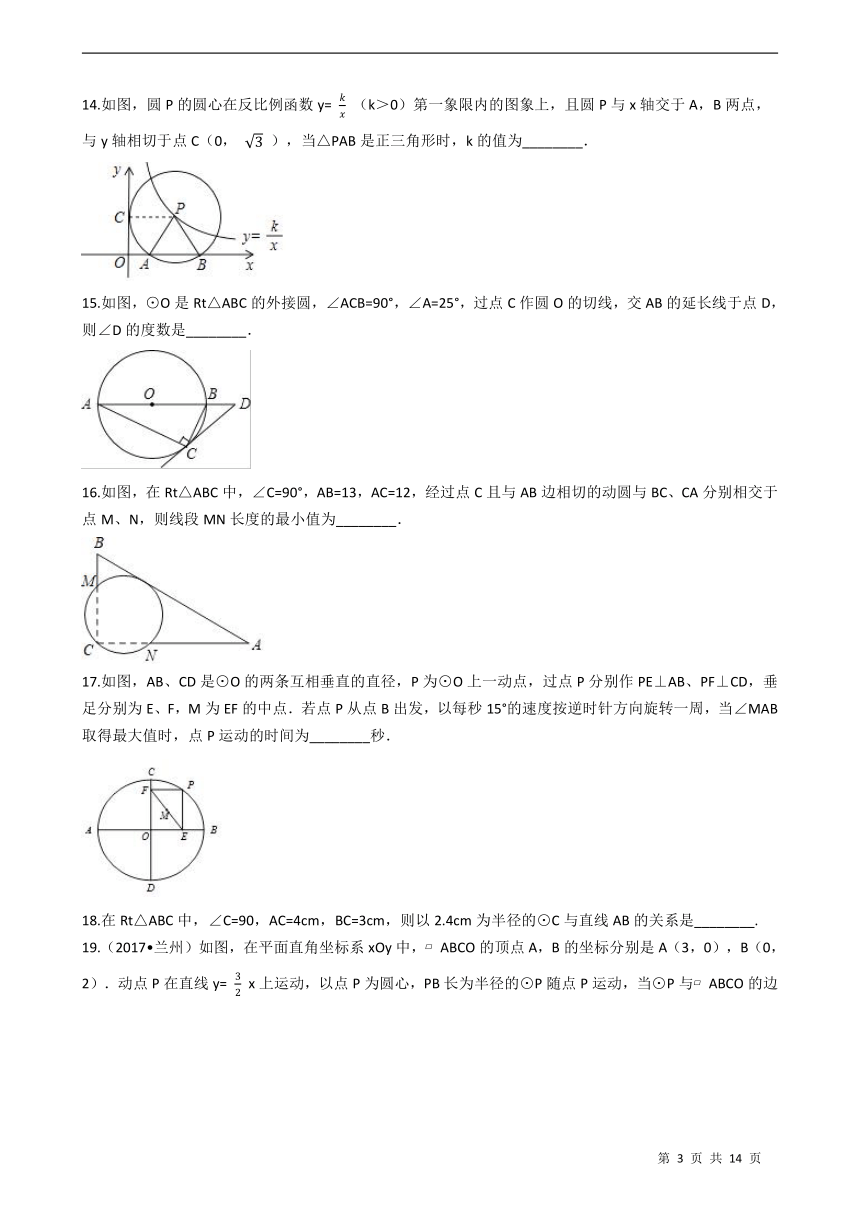
3.如图,⊙O是△ABC的内切圆,则点O是△ABC的(?? )
A.?三条边的垂直平分线的交点??????B.?三条角平分线的交点??????C.?三条中线的交点??????D.?三条高的交点
4.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A = 70°,则∠BOC的度数为(?? )
A.?100°????????????????????????????????????B.?110°????????????????????????????????????C.?120°????????????????????????????????????D.?130°
5.如图,点A,B,D在☉O上,∠A=25°,OD的延长线交直线BC于点C,当∠OCB=(?? )时,直线BC与☉O相切.
A.?25°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
6.如图,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,则AB的长为( )
A.?4cm?????????????????????????????????????B.?5cm?????????????????????????????????????C.?6cm?????????????????????????????????????D.?8cm
7.如图,PA、PB是⊙O的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于( )
?
A.?60°?????????????????????????????????????B.?90°?????????????????????????????????????C.?120°?????????????????????????????????????D.?150°
8.在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定(??)
A.?与x轴相离、与y轴相切???????????????????????????????????????B.?与x轴、y轴都相离
C.?与x轴相切、与y轴相离???????????????????????????????????????D.?与x轴、y轴都相切
9.如图,已知AB是⊙O的直径,AD切⊙O于点A,=. 则下列结论中不一定正确的是(?? )
A.?
BA⊥DA
?????????????????????????B.?OC//AE?????????????????????????C.?∠COE=2∠CAE?????????????????????????D.?OD⊥AC
10.已知OA平分∠BOC,P是OA上任意一点,如果以P为圆心的圆与OC相离,那么⊙P与OB的位置关系是(?????)
A.?相离??????????????????????????????????B.?相切??????????????????????????????????C.?相交??????????????????????????????????D.?不能确定
二、填空题(共10题;共30分)
11.如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为________.
12.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=________°.
13.如图, 是 的直径, 是 上的点,过点 作 的切线交 的延长线于点 .若∠A=32°,则 ________度.
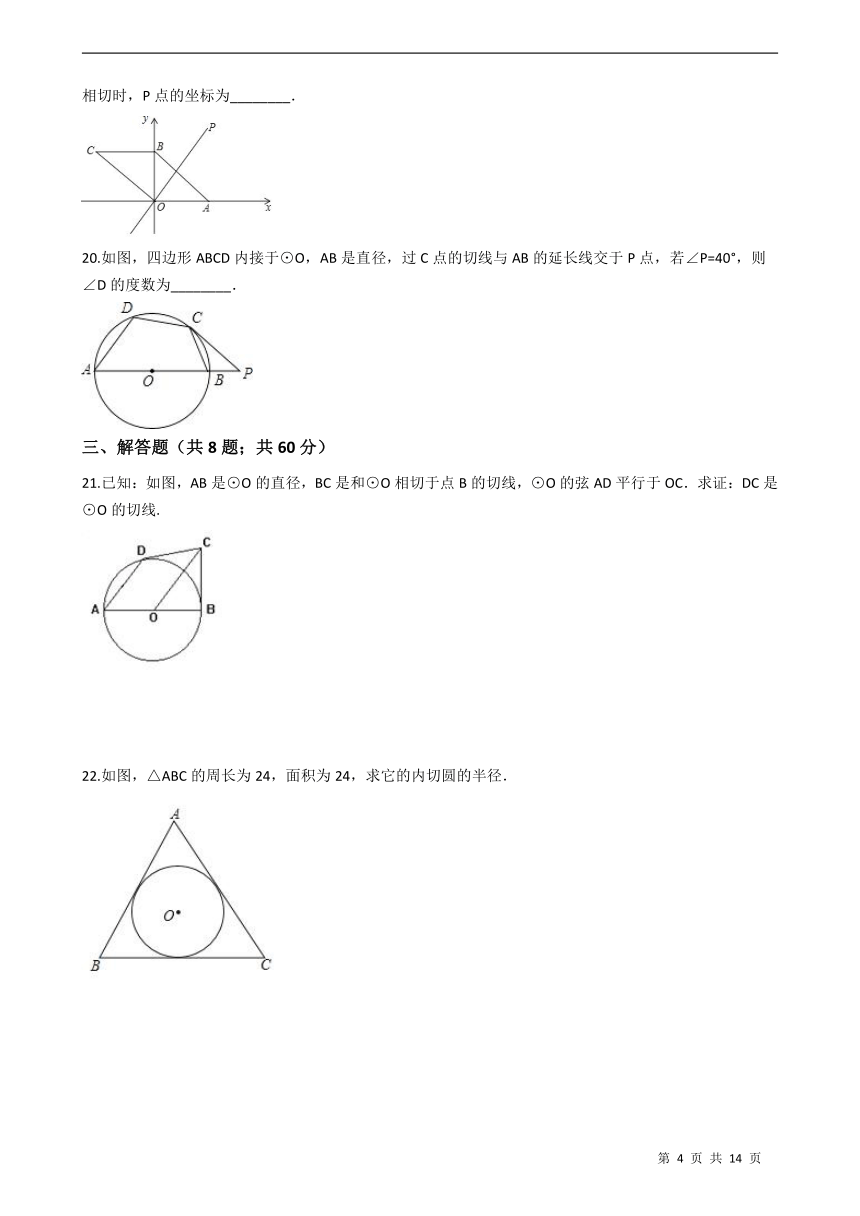
14.如图,圆P的圆心在反比例函数y= (k>0)第一象限内的图象上,且圆P与x轴交于A,B两点,与y轴相切于点C(0, ),当△PAB是正三角形时,k的值为________.
15.如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是________.
16.如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为________.
17.如图,AB、CD是⊙O的两条互相垂直的直径,P为⊙O上一动点,过点P分别作PE⊥AB、PF⊥CD,垂足分别为E、F,M为EF的中点.若点P从点B出发,以每秒15°的速度按逆时针方向旋转一周,当∠MAB 取得最大值时,点P运动的时间为________秒.
18.在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,则以2.4cm为半径的⊙C与直线AB的关系是________.
19.(2017?兰州)如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y= x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为________.
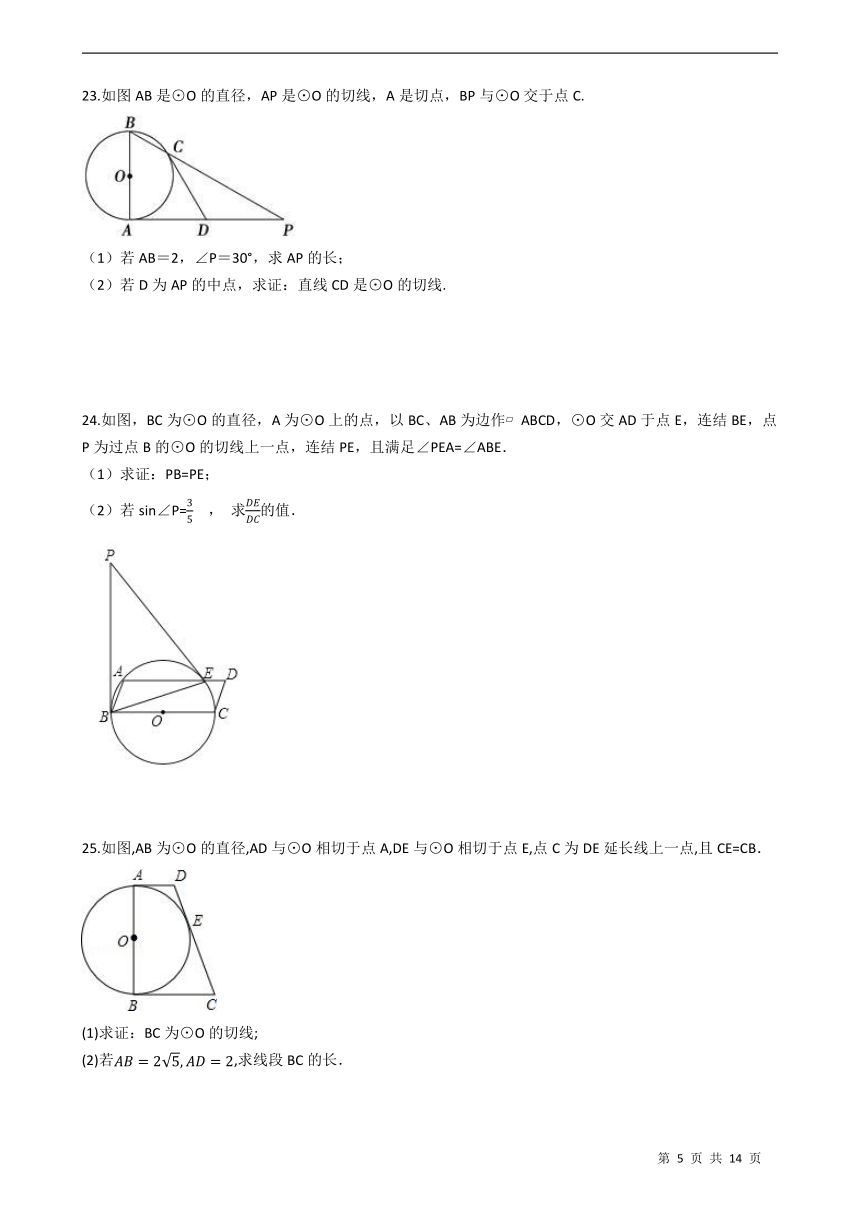
20.如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为________.
三、解答题(共8题;共60分)
21.已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线.
22.如图,△ABC的周长为24,面积为24,求它的内切圆的半径.
23.如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)若AB=2,∠P=30°,求AP的长;
(2)若D为AP的中点,求证:直线CD是⊙O的切线.
24.如图,BC为⊙O的直径,A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交AD于点E,连结BE,点P为过点B的⊙O的切线上一点,连结PE,且满足∠PEA=∠ABE.
(1)求证:PB=PE;
(2)若sin∠P= , 求的值.
25.如图,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若,求线段BC的长.
26.如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=70°,求∠APB的度数.
27.如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC.
(1)猜想:线段OD与BC有何数量和位置关系,并证明你的结论.
(2)求证:PC是⊙O的切线.
28.如图,在平面直角坐标系xOy中,点A、B坐标分别为(4,2)、(0,2),线段CD在于x轴上,CD= , 点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
(1)求线段CE的长;
(2)记S为RtΔCDE与ΔABO的重叠部分面积,试写出S关于t的函数关系式及t的取值范围;
(3)连结DF,
①当t取何值时,有DF=CD?
②直接写出ΔCDF的外接圆与OA相切时t的值.
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】C
8.【答案】A
9.【答案】D
10.【答案】A
二、填空题
11.【答案】115°
12.【答案】44
13.【答案】26
14.【答案】2
15.【答案】40°
16.【答案】
17.【答案】8或16
18.【答案】相切
19.【答案】(0,0)或( ,1)或(3﹣ , )
20.【答案】115°
三、解答题
21.【答案】证明:连接OD;
∵AD平行于OC,
∴∠COD=∠ODA,∠COB=∠A;
∵∠ODA=∠A,
∴∠COD=∠COB,OC=OC,OD=OB,
∴△OCD≌△OCB,
∴∠CDO=∠CBO=90°.
∴DC是⊙O的切线.
22.【答案】解:连结OA、OB、OC,作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,
设它的内切圆的半径为r,则OD=OE=OF=r,
∵S△ABC=S△AOB+S△OBC+S△OAC ,
∴?r?AB+?r?BC+?r?AC=24,
∴r(AB+BC+AC)=24,
∴r?24=24,
∴r=2.
即它的内切圆的半径为2.
23.【答案】解:(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,∴∠BAP=90°;
又∵AB=2,∠P=30°,
∴AP===2,
即AP=2.
(2)证明:如图,连接OC,OD、AC.
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD(直角三角形斜边上的中线等于斜边的一半);
在△OAD和△OCD中,
,
∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD(全等三角形的对应角相等);
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,即直线CD是⊙O的切线.
24.【答案】解:(1)证明:∵PB是⊙O的切线,
∴∠ABP=∠AEB,
∵∠PEA=∠ABE.
∴∠PBE=∠PEB,
∴PB=PE;
(2)连接EC,延长DA交PB于F,
∵PB是⊙O的切线,
∴BC⊥PB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴EF⊥PB,
∵sin∠P=,
设PE=5a,EF=3a,则PF=4a,
∵PB=PE=5a,
∴BF=a,
∴BE==a,
∴=,
∵AD∥BC,
∴=,
∴AB=CE,
∵AB=CD,
∴CE=CD,
∴∠D=∠CED,
∵AD∥BC,
∴∠AEB=∠EBC,
∵∠ABP=∠AEB,
∴∠ABP=∠EBC,
∴∠PBE=∠ABC,
∴∠PBE=∠D,
∵∠PBE=∠PEB,
∴△CDE∽△PBE,
∴==;
25.【答案】解:(1)连接OE、OC.
∵CB=CE,OB=OE,OC=OC,
∴△OBC≌△OEC.
∴∠OBC=∠OEC.
又∵DE与⊙O相切于点E,
∴∠OEC=90°.
∴∠OBC=90°.
∴BC为⊙O的切线.
(2)过点D作DF⊥BC于点F,则四边形ABFD是矩形,BF=AD=2,DF=AB=2.
∵AD、DC、BC分别切⊙O于点A、E、B,
∴DA=DE,CE=CB.
设BC为x,则CF=x﹣2,DC=x+2.
在Rt△DFC中,(x+2)2﹣(x﹣2)2=(2)2,解得x=.
∴BC=.
26.【答案】解:如图,连接AB;
∵PA、PB是⊙O的切线,
∴∠PAB=∠PBA=∠ACB=70°,
∴∠P=180°-2×70°=40°,
即∠P的度数为40°.
27.【答案】解:(1)猜想:OD∥BC,OD=BC.
证明:∵OD⊥AC,
∴AD=DC
∵AB是⊙O的直径,
∴OA=OB
∴OD是△ABC的中位线,
∴OD∥BC,OD=BC
(2)证明:连接OC,设OP与⊙O交于点E.如图:
∵OD⊥AC,OD经过圆心O,
∴弧AE=弧CE,即∠AOE=∠COE
在△OAP和△OCP中,
,
∴△OAP≌△OCP,
∴∠OCP=∠OAP
∵PA是⊙O的切线,
∴∠OAP=90°.
∴∠OCP=90°,即OC⊥PC
∴PC是⊙O的切线.
28.【答案】解:(1)∵在Rt△CDE中,CD=,DE=2,
∴CE==;
(2)如图1,作FH⊥CD于H.
∵AB∥OD,DE⊥OD,OB⊥OD,
∴四边形ODEB是矩形,
∴BE=OD,
∵OC=t,
∴BE=OD=OC+CD=t+,
∴AE=AB﹣BE=4﹣(t+)=﹣t,
∵AB∥OD,
∴△OCF∽△AEF,△ODG∽△AEG,
∴,,
又∵CF+EF=5,DG+EG=4,
∴,,
∴CF=t,EG=,
∴EF=CE﹣CF=5﹣t,
∵FH∥ED,
∴,即HD=?CD=(﹣t),
∴S=EG?HD=××(﹣t)=(﹣t)2 ,
t的取值范围为:0≤t≤;
(3)①由(2)知CF=t,
如图2,当DF=CD时,如图作DK⊥CF于K,
则CK=CF=t,
∵CK=CDcos∠DCE,
∴t=3×,
解得:t=;
∴当t=时,DF=CD;
②∵点A,B坐标分别为(8,4),(0,4),
∴AB=8,OB=4,
∴OA=,
∵由(2)知HD=(5﹣t),
∴OH=t+3﹣(5﹣t)=,
∵∠A+∠AOB=∠AOD+∠AOB=90°,
∴∠A=∠AOD,
∴Rt△AOB∽Rt△OFH,
∴,
解得OF=,
∵当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,
∴OF2=OC?OD,即()2=t(t+3),得t=.
一、单选题(共10题;共30分)
1.到三角形三边距离都相等的点是三角形(???)的交点
A.?三边中垂线????????????????????????B.?三条中线????????????????????????C.?三条高????????????????????????D.?三条内角平分线
2.已知直线l与半径为r的☉O相交,且点O到直线l的距离为6,则r的取值范围是(?? )
A.?r<6??????????????????????????????????????B.?r=6??????????????????????????????????????C.?r>6??????????????????????????????????????D.?r≥6
3.如图,⊙O是△ABC的内切圆,则点O是△ABC的(?? )
A.?三条边的垂直平分线的交点??????B.?三条角平分线的交点??????C.?三条中线的交点??????D.?三条高的交点
4.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A = 70°,则∠BOC的度数为(?? )
A.?100°????????????????????????????????????B.?110°????????????????????????????????????C.?120°????????????????????????????????????D.?130°
5.如图,点A,B,D在☉O上,∠A=25°,OD的延长线交直线BC于点C,当∠OCB=(?? )时,直线BC与☉O相切.
A.?25°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
6.如图,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,则AB的长为( )
A.?4cm?????????????????????????????????????B.?5cm?????????????????????????????????????C.?6cm?????????????????????????????????????D.?8cm
7.如图,PA、PB是⊙O的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于( )
?
A.?60°?????????????????????????????????????B.?90°?????????????????????????????????????C.?120°?????????????????????????????????????D.?150°
8.在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定(??)
A.?与x轴相离、与y轴相切???????????????????????????????????????B.?与x轴、y轴都相离
C.?与x轴相切、与y轴相离???????????????????????????????????????D.?与x轴、y轴都相切
9.如图,已知AB是⊙O的直径,AD切⊙O于点A,=. 则下列结论中不一定正确的是(?? )
A.?
BA⊥DA
?????????????????????????B.?OC//AE?????????????????????????C.?∠COE=2∠CAE?????????????????????????D.?OD⊥AC
10.已知OA平分∠BOC,P是OA上任意一点,如果以P为圆心的圆与OC相离,那么⊙P与OB的位置关系是(?????)
A.?相离??????????????????????????????????B.?相切??????????????????????????????????C.?相交??????????????????????????????????D.?不能确定
二、填空题(共10题;共30分)
11.如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为________.
12.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=________°.
13.如图, 是 的直径, 是 上的点,过点 作 的切线交 的延长线于点 .若∠A=32°,则 ________度.
14.如图,圆P的圆心在反比例函数y= (k>0)第一象限内的图象上,且圆P与x轴交于A,B两点,与y轴相切于点C(0, ),当△PAB是正三角形时,k的值为________.
15.如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是________.
16.如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为________.
17.如图,AB、CD是⊙O的两条互相垂直的直径,P为⊙O上一动点,过点P分别作PE⊥AB、PF⊥CD,垂足分别为E、F,M为EF的中点.若点P从点B出发,以每秒15°的速度按逆时针方向旋转一周,当∠MAB 取得最大值时,点P运动的时间为________秒.
18.在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,则以2.4cm为半径的⊙C与直线AB的关系是________.
19.(2017?兰州)如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y= x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为________.
20.如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为________.
三、解答题(共8题;共60分)
21.已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线.
22.如图,△ABC的周长为24,面积为24,求它的内切圆的半径.
23.如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)若AB=2,∠P=30°,求AP的长;
(2)若D为AP的中点,求证:直线CD是⊙O的切线.
24.如图,BC为⊙O的直径,A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交AD于点E,连结BE,点P为过点B的⊙O的切线上一点,连结PE,且满足∠PEA=∠ABE.
(1)求证:PB=PE;
(2)若sin∠P= , 求的值.
25.如图,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若,求线段BC的长.
26.如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=70°,求∠APB的度数.
27.如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC.
(1)猜想:线段OD与BC有何数量和位置关系,并证明你的结论.
(2)求证:PC是⊙O的切线.
28.如图,在平面直角坐标系xOy中,点A、B坐标分别为(4,2)、(0,2),线段CD在于x轴上,CD= , 点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
(1)求线段CE的长;
(2)记S为RtΔCDE与ΔABO的重叠部分面积,试写出S关于t的函数关系式及t的取值范围;
(3)连结DF,
①当t取何值时,有DF=CD?
②直接写出ΔCDF的外接圆与OA相切时t的值.
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】C
8.【答案】A
9.【答案】D
10.【答案】A
二、填空题
11.【答案】115°
12.【答案】44
13.【答案】26
14.【答案】2
15.【答案】40°
16.【答案】
17.【答案】8或16
18.【答案】相切
19.【答案】(0,0)或( ,1)或(3﹣ , )
20.【答案】115°
三、解答题
21.【答案】证明:连接OD;
∵AD平行于OC,
∴∠COD=∠ODA,∠COB=∠A;
∵∠ODA=∠A,
∴∠COD=∠COB,OC=OC,OD=OB,
∴△OCD≌△OCB,
∴∠CDO=∠CBO=90°.
∴DC是⊙O的切线.
22.【答案】解:连结OA、OB、OC,作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,
设它的内切圆的半径为r,则OD=OE=OF=r,
∵S△ABC=S△AOB+S△OBC+S△OAC ,
∴?r?AB+?r?BC+?r?AC=24,
∴r(AB+BC+AC)=24,
∴r?24=24,
∴r=2.
即它的内切圆的半径为2.
23.【答案】解:(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,∴∠BAP=90°;
又∵AB=2,∠P=30°,
∴AP===2,
即AP=2.
(2)证明:如图,连接OC,OD、AC.
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD(直角三角形斜边上的中线等于斜边的一半);
在△OAD和△OCD中,
,
∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD(全等三角形的对应角相等);
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,即直线CD是⊙O的切线.
24.【答案】解:(1)证明:∵PB是⊙O的切线,
∴∠ABP=∠AEB,
∵∠PEA=∠ABE.
∴∠PBE=∠PEB,
∴PB=PE;
(2)连接EC,延长DA交PB于F,
∵PB是⊙O的切线,
∴BC⊥PB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴EF⊥PB,
∵sin∠P=,
设PE=5a,EF=3a,则PF=4a,
∵PB=PE=5a,
∴BF=a,
∴BE==a,
∴=,
∵AD∥BC,
∴=,
∴AB=CE,
∵AB=CD,
∴CE=CD,
∴∠D=∠CED,
∵AD∥BC,
∴∠AEB=∠EBC,
∵∠ABP=∠AEB,
∴∠ABP=∠EBC,
∴∠PBE=∠ABC,
∴∠PBE=∠D,
∵∠PBE=∠PEB,
∴△CDE∽△PBE,
∴==;
25.【答案】解:(1)连接OE、OC.
∵CB=CE,OB=OE,OC=OC,
∴△OBC≌△OEC.
∴∠OBC=∠OEC.
又∵DE与⊙O相切于点E,
∴∠OEC=90°.
∴∠OBC=90°.
∴BC为⊙O的切线.
(2)过点D作DF⊥BC于点F,则四边形ABFD是矩形,BF=AD=2,DF=AB=2.
∵AD、DC、BC分别切⊙O于点A、E、B,
∴DA=DE,CE=CB.
设BC为x,则CF=x﹣2,DC=x+2.
在Rt△DFC中,(x+2)2﹣(x﹣2)2=(2)2,解得x=.
∴BC=.
26.【答案】解:如图,连接AB;
∵PA、PB是⊙O的切线,
∴∠PAB=∠PBA=∠ACB=70°,
∴∠P=180°-2×70°=40°,
即∠P的度数为40°.
27.【答案】解:(1)猜想:OD∥BC,OD=BC.
证明:∵OD⊥AC,
∴AD=DC
∵AB是⊙O的直径,
∴OA=OB
∴OD是△ABC的中位线,
∴OD∥BC,OD=BC
(2)证明:连接OC,设OP与⊙O交于点E.如图:
∵OD⊥AC,OD经过圆心O,
∴弧AE=弧CE,即∠AOE=∠COE
在△OAP和△OCP中,
,
∴△OAP≌△OCP,
∴∠OCP=∠OAP
∵PA是⊙O的切线,
∴∠OAP=90°.
∴∠OCP=90°,即OC⊥PC
∴PC是⊙O的切线.
28.【答案】解:(1)∵在Rt△CDE中,CD=,DE=2,
∴CE==;
(2)如图1,作FH⊥CD于H.
∵AB∥OD,DE⊥OD,OB⊥OD,
∴四边形ODEB是矩形,
∴BE=OD,
∵OC=t,
∴BE=OD=OC+CD=t+,
∴AE=AB﹣BE=4﹣(t+)=﹣t,
∵AB∥OD,
∴△OCF∽△AEF,△ODG∽△AEG,
∴,,
又∵CF+EF=5,DG+EG=4,
∴,,
∴CF=t,EG=,
∴EF=CE﹣CF=5﹣t,
∵FH∥ED,
∴,即HD=?CD=(﹣t),
∴S=EG?HD=××(﹣t)=(﹣t)2 ,
t的取值范围为:0≤t≤;
(3)①由(2)知CF=t,
如图2,当DF=CD时,如图作DK⊥CF于K,
则CK=CF=t,
∵CK=CDcos∠DCE,
∴t=3×,
解得:t=;
∴当t=时,DF=CD;
②∵点A,B坐标分别为(8,4),(0,4),
∴AB=8,OB=4,
∴OA=,
∵由(2)知HD=(5﹣t),
∴OH=t+3﹣(5﹣t)=,
∵∠A+∠AOB=∠AOD+∠AOB=90°,
∴∠A=∠AOD,
∴Rt△AOB∽Rt△OFH,
∴,
解得OF=,
∵当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,
∴OF2=OC?OD,即()2=t(t+3),得t=.
