第4章 相似三角形单元综合训练题(含答案)
文档属性
| 名称 | 第4章 相似三角形单元综合训练题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-30 08:52:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教九年级数学《相似三角形》综合训练题
(难度系数0.4左右)
选择题(每小题3分,共30分)
1.若点C是线段AB的黄金分割点,且AB=2(AC>BC),则AC等于( )
A. B. C. D.或
2.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使△ABC∽△CAD,只要CD等于(?? )
A.?? ???B. ????? C.????????? D.?
3.如图,在ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF∶FC等于(????)
A.3∶2????????? B.3∶1????????? C.1∶ D.1∶2
4.如图,P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是(????)
A.∠ABP=∠C??? B.∠APB=∠ABC??? C.?? ?? D.?
5.如图,△ABC?中,D?为?AC?边上一点,∠DBC=∠A,BC=,AC=3,则?CD?长为(?? )
A.1????????????? ? B.?????????????????????????????C.2????? D.
6.如图,在ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S?AEPH=( )
A.3 B.4 C.5 D.6
7.如图,△ABC中有一正方形DEFG,其中D在AC上,E、F在AB 上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=8,BC=6,EF=2,则BN的长度为( )
A. B. C. D.
8.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点C,连接DG,BF,给出以下结论:①△DAG≌△DFG;②EG=10;③BG=2AG;④△EBF∽△DEG,其中所有正确结论的个数是( )
A.1 B.2 C.3 D.4
9.如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB延长线于E,则图中一定相似的三角形是( )
A.△AED与△ACB B.△AEB与△ACD C.△BAE与△ACE D.△AEC与△DAC
10.如图,在正方形ABCD中,以BC为边作等边△BPC,延长BP,CP分别交AD于点E,F,连接BD,DP,BD与CF相较于点H,给出下列结论:①AE=CF;②ED2=EP?EB;③△PFD∽△PDB;④∠BPD=135°,其中正确的是( )
①②③④ B.②③
C.①②④ D.①③④
填空题(每小题3分,共18分)
11.如图,DE是△ABC的中位线,CD、BE交于点F,若△DEF面积是1,则△BCF的面积是 ??? .
12.如图,在平行四边形ABCD中,E为边BC上一点,AC与DE相交于点F,若CE=2EB,S△AFD=9,则S△EFC等于 .
13.如图1,△ABC是一张等腰直角三角形彩色纸,AC=BC,将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.若用这4张纸条刚好可以为一幅正方形美术作品镶边(纸条不重叠),如图2,则正方形美术作品与镶边后的作品的面积之比为 .
14.如图,在平面直角坐标系中,点P的坐标为(2,0),直线与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM的最小值为 .
如图,正方形ABCD的边长为12,其内部有一个小正方形EFGH,其中E、F、H分别在BC,CD,AE上.若BE=9,则小正方形EFGH的边长 .
16.如图,点B1在直线l:上,点B1的横坐标为2,过B1作B1A1⊥1,交x轴于点A1,以A1B1为边,向右作正方形A1B1B2C1,延长B2C1交x轴于点A2;以A2B2为边,向右作正方形A2B2B3C2,延长B3C2交x轴于点A3;以A3B3为边,向右作正方形A3B3B4C3延长B4C3交x轴于点A4;…;按照这个规律进行下去,点Cn的横坐标为 ??? (结果用含正整数n的代数式表示).
解答题:(7小题,共52分)
17.(6分)如图,在平行四边形ABCD中,E是BC上的一点,且BE:CE=1:2,AE交BD于点F,求:
(1)求的值;
(2)△BEF与△DAF的周长比、面积的比.
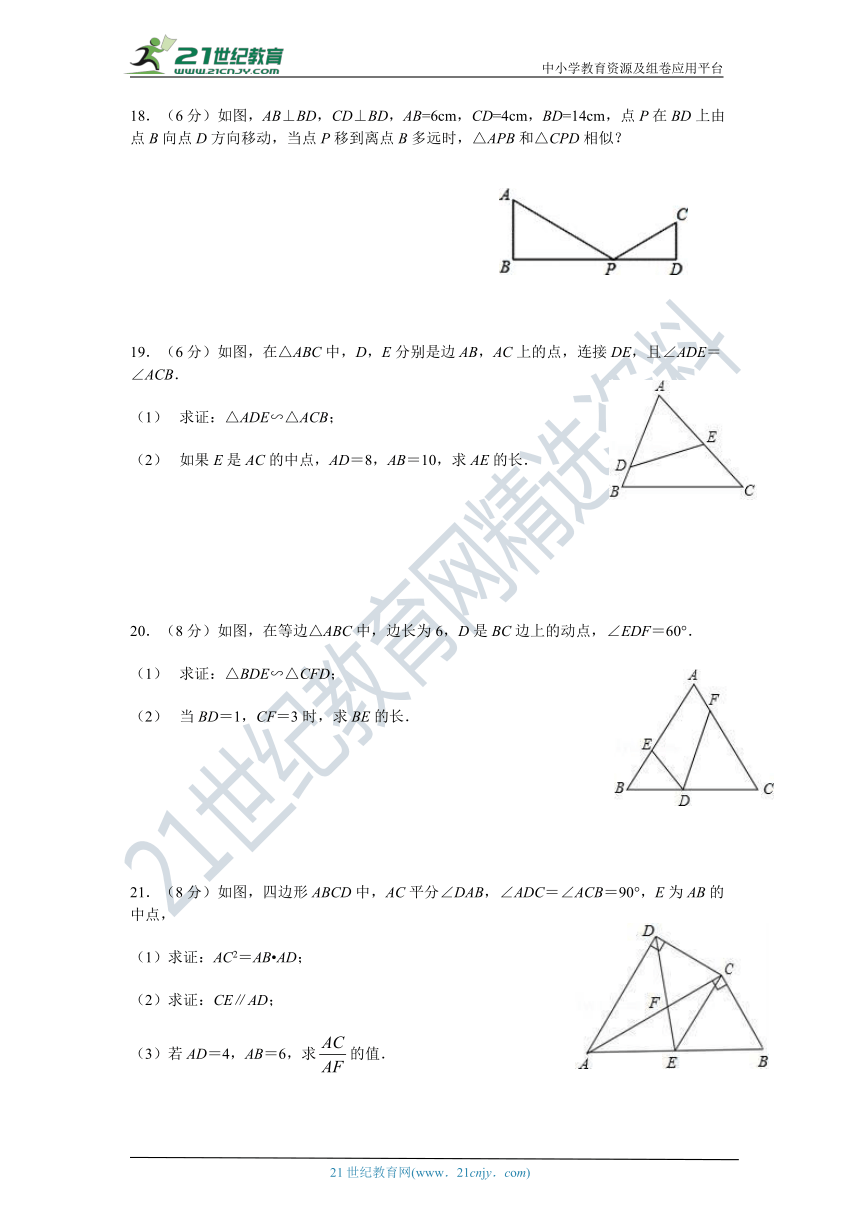
18.(6分)如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
19.(6分)如图,在△ABC?中,D,E?分别是边?AB,AC?上的点,连接?DE,且∠ADE=∠ACB.
(1)???求证:△ADE∽△ACB;
(2)???如果?E?是?AC?的中点,AD=8,AB=10,求?AE?的长.
20.(8分)如图,在等边△ABC?中,边长为?6,D?是?BC?边上的动点,∠EDF=60°.
(1)???求证:△BDE∽△CFD;
(2)???当?BD=1,CF=3?时,求?BE?的长.
21.(8分)如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB?AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求的值.
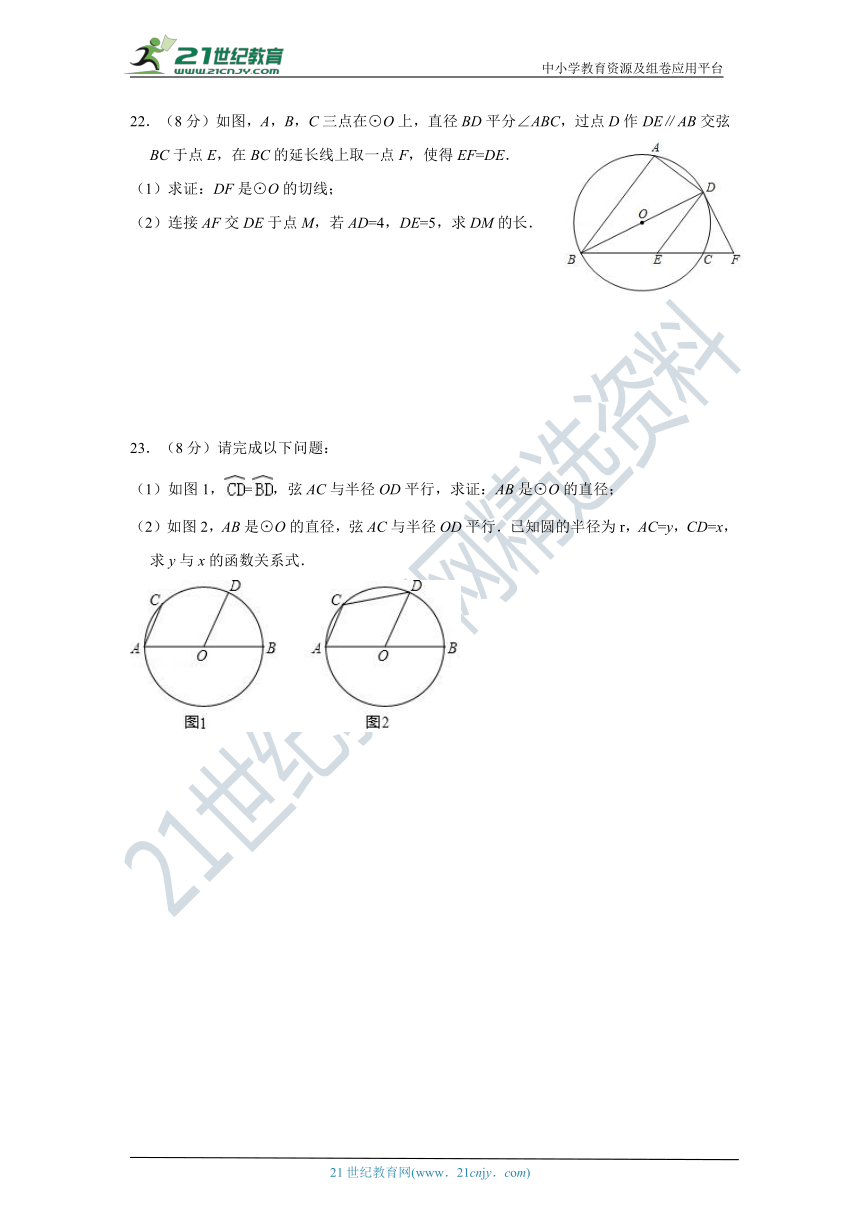
22.(8分)如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,在BC的延长线上取一点F,使得EF=DE.
(1)求证:DF是⊙O的切线;
(2)连接AF交DE于点M,若AD=4,DE=5,求DM的长.
23.(8分)请完成以下问题:
(1)如图1,=,弦AC与半径OD平行,求证:AB是⊙O的直径;
(2)如图2,AB是⊙O的直径,弦AC与半径OD平行.已知圆的半径为r,AC=y,CD=x,求y与x的函数关系式.
答案:
选择题
ADDDC BCCCC
填空题:
11.4 12.4 13. 14.4 15. 16.
三、解答题
17.(1)在平行四边形ABCD中
AD=BC,AD∥BC
∴△BEF∽△ADF,
∴,
又∵BE:CE=1:2
∴.
(2)∵△BEF∽△DAF
∴周长之比为,
∴面积之比为
18.解:∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴当或时,△PAB与△PCD是相似三角形,
∵AB=6cm,CD=4cm,BD=14cm,
∴或,
解得:BP=2或12或,
即BP=2或12或时,△PAB与△PCD是相似三角形.
19.(1)∵∠ADE=∠ACB,∠A=∠A,
∴△ADE∽△ACB;
(2)由(1)可知:△ADE∽△ACB,
∵点?E?是?AC?的中点,设?AE=x,
∴AC=2AE=2x,
∵AD=8,AB=10,
∴?,
解得:
20.(1)证明:∵△ABC?为等边三角形,
∴∠B=∠C=60°,
∵∠EDF=60°,
∴∠BED+∠EDB=∠EDB+∠FDC=120°,
∴∠BED=∠FDC,
∴△BDE∽△CFD;
(2)解:由(1)知△BDE∽△CFD,
∵BC=6,BD=1,
∴CD=BC﹣BD=5,
∴?,?解 得?BE=?.
21.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB?AD;
(2)证明:∵E为AB的中点,
∴CE=AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=AB,
∴CE=3,
∵AD=4,
∴
22.(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD.
∵DE∥AB,
∴∠ABD=∠BDE.
∴∠CBD=∠BDE.
∵ED=EF,
∴∠EDF=∠EFD.
∵∠EDF+∠EFD+∠EDB+∠EBD=180°,
∴∠BDF=∠BDE+∠EDF=90°.
∴OD⊥DF.
∵OD是半径,
∴DF是⊙O的切线.
(2)解:连接DC,
∵BD是⊙O的直径,
∴∠BAD=∠BCD=90°.
∵∠ABD=∠CBD,BD=BD,
∴△ABD≌△CBD.
∴CD=AD=4,AB=BC.
∵DE=5,
∴CE=3,EF=DE=5.
∵∠CBD=∠BDE,
∴BE=DE=5.
∴BF=BE+EF=10,BC=BE+EC=8.
∴AB=8.
∵DE∥AB,
∴△ABF∽△MEF.
∴ME=4.
∴DM=DE﹣EM=1.
23.解:
(1)证明:连结BC,交OD于点H,(如图1)
∵,
∴OD⊥BC,
即∠OHB=90°,
∵弦AC与半径OD平行,
∴∠ACB=∠OHB=90°,
∴弦AB是圆的直径(90°的圆周角所对的弦是直径);
(2)如图2,连结AD,BD,连结BC交OD于点H,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵弦AC与半径OD平行,
∴∠ACB=∠OHB=90°,
∴OD⊥BC,
∴,
∴CD=BD=x,
∴∠DBC=∠DAB,
∴△DBH∽△DAB,
∵O是AB的中点,
∴OH是△ABC的中位线,
∴OH=AC=y,
∴DH=OD﹣OH=r﹣y,
即,
化简得:.
第2题图 第3题图 第4题图 第5题图
第6题图 第7题图 第8题图 第9题图
第11题图 第11题图 第13题图
第14题图 第15题图 第16题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
