2019年浙教新版八年级上册数学《第4章 图形与坐标》单元测试卷(解析版)
文档属性
| 名称 | 2019年浙教新版八年级上册数学《第4章 图形与坐标》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 418.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-29 21:55:16 | ||
图片预览

文档简介
2019年浙教新版八年级上册数学《第4章 图形与坐标》单元测试卷
一.选择题(共10小题)
1.若x轴上的点P到y轴的距离是3,则点P的坐标为( )
A.(3,0) B.(3,0)或 (﹣3,0)
C.(3,0) D.(0,3)或 (0,﹣3)
2.如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第80秒时质点所在位置的坐标是( )
A.(0,9) B.(9,0) C.(0,8) D.( 8,0)
3.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(﹣3,3) B.(0,3) C.(3,2) D.(1,3)
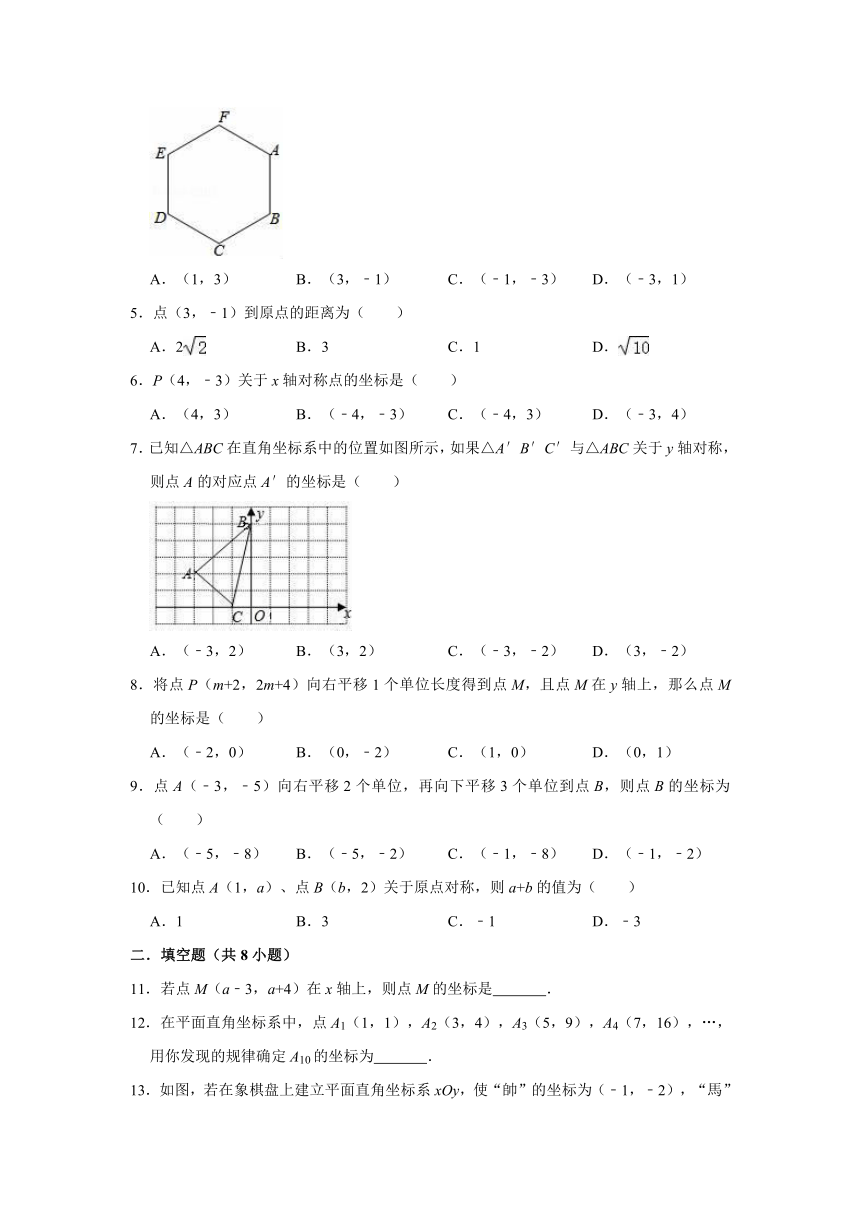
4.如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(﹣a,b),则点D的坐标为( )
A.(1,3) B.(3,﹣1) C.(﹣1,﹣3) D.(﹣3,1)
5.点(3,﹣1)到原点的距离为( )
A.2 B.3 C.1 D.
6.P(4,﹣3)关于x轴对称点的坐标是( )
A.(4,3) B.(﹣4,﹣3) C.(﹣4,3) D.(﹣3,4)
7.已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,则点A的对应点A′的坐标是( )
A.(﹣3,2) B.(3,2) C.(﹣3,﹣2) D.(3,﹣2)
8.将点P(m+2,2m+4)向右平移1个单位长度得到点M,且点M在y轴上,那么点M的坐标是( )
A.(﹣2,0) B.(0,﹣2) C.(1,0) D.(0,1)
9.点A(﹣3,﹣5)向右平移2个单位,再向下平移3个单位到点B,则点B的坐标为( )
A.(﹣5,﹣8) B.(﹣5,﹣2) C.(﹣1,﹣8) D.(﹣1,﹣2)
10.已知点A(1,a)、点B(b,2)关于原点对称,则a+b的值为( )
A.1 B.3 C.﹣1 D.﹣3
二.填空题(共8小题)
11.若点M(a﹣3,a+4)在x轴上,则点M的坐标是 .
12.在平面直角坐标系中,点A1(1,1),A2(3,4),A3(5,9),A4(7,16),…,用你发现的规律确定A10的坐标为 .
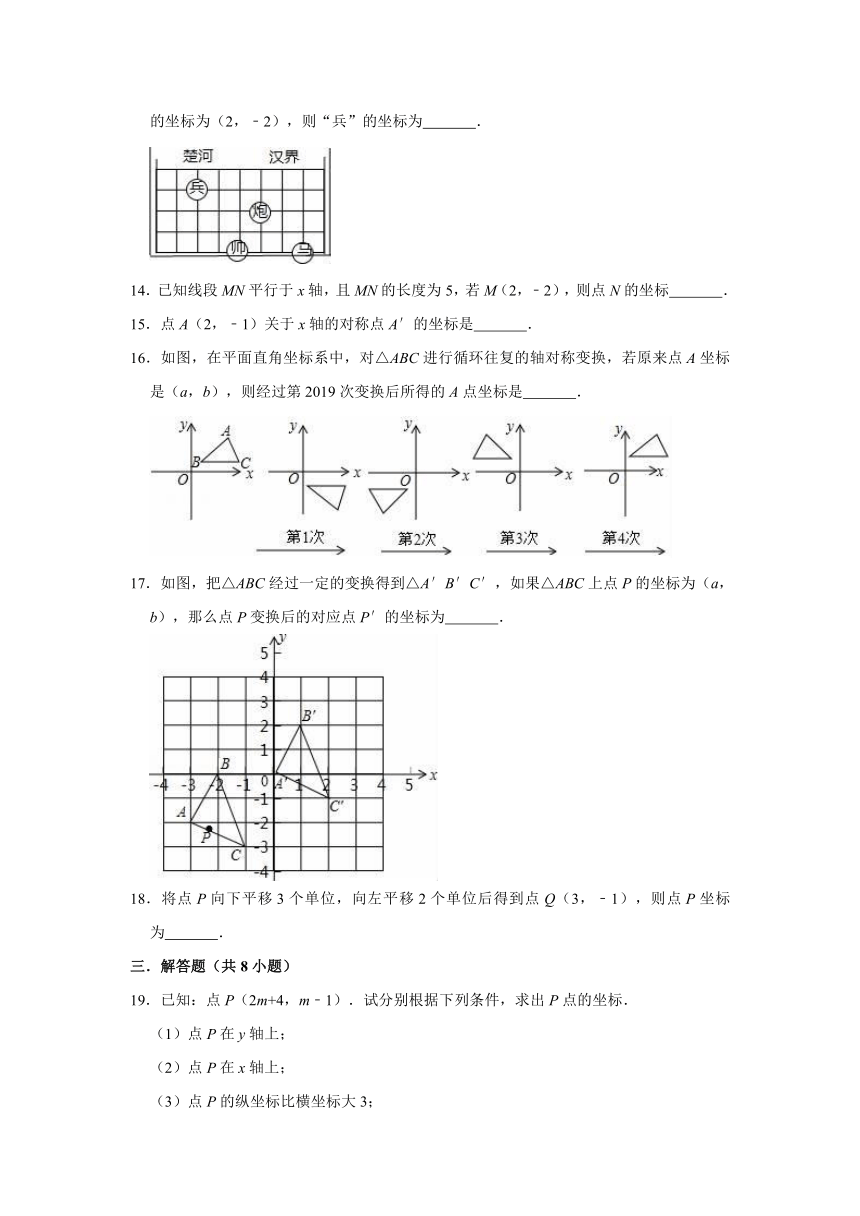
13.如图,若在象棋盘上建立平面直角坐标系xOy,使“帥”的坐标为(﹣1,﹣2),“馬”的坐标为(2,﹣2),则“兵”的坐标为 .
14.已知线段MN平行于x轴,且MN的长度为5,若M(2,﹣2),则点N的坐标 .
15.点A(2,﹣1)关于x轴的对称点A′的坐标是 .
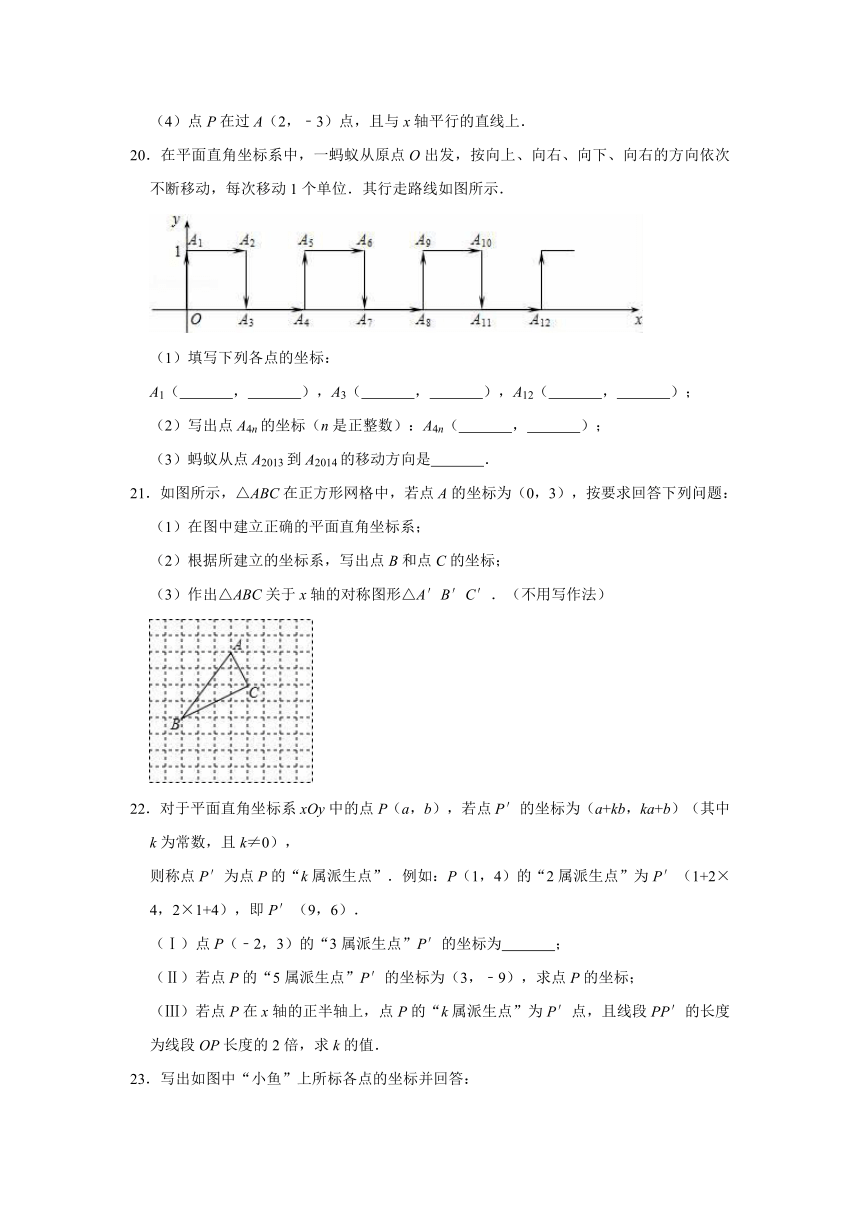
16.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2019次变换后所得的A点坐标是 .
17.如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为 .
18.将点P向下平移3个单位,向左平移2个单位后得到点Q(3,﹣1),则点P坐标为 .
三.解答题(共8小题)
19.已知:点P(2m+4,m﹣1).试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过A(2,﹣3)点,且与x轴平行的直线上.
20.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.
(1)填写下列各点的坐标:
A1( , ),A3( , ),A12( , );
(2)写出点A4n的坐标(n是正整数):A4n( , );
(3)蚂蚁从点A2013到A2014的移动方向是 .
21.如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
22.对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
23.写出如图中“小鱼”上所标各点的坐标并回答:
(1)点B、E的位置有什么特点;
(2)从点B与点E,点C与点D的位置看,它们的坐标有什么特点?
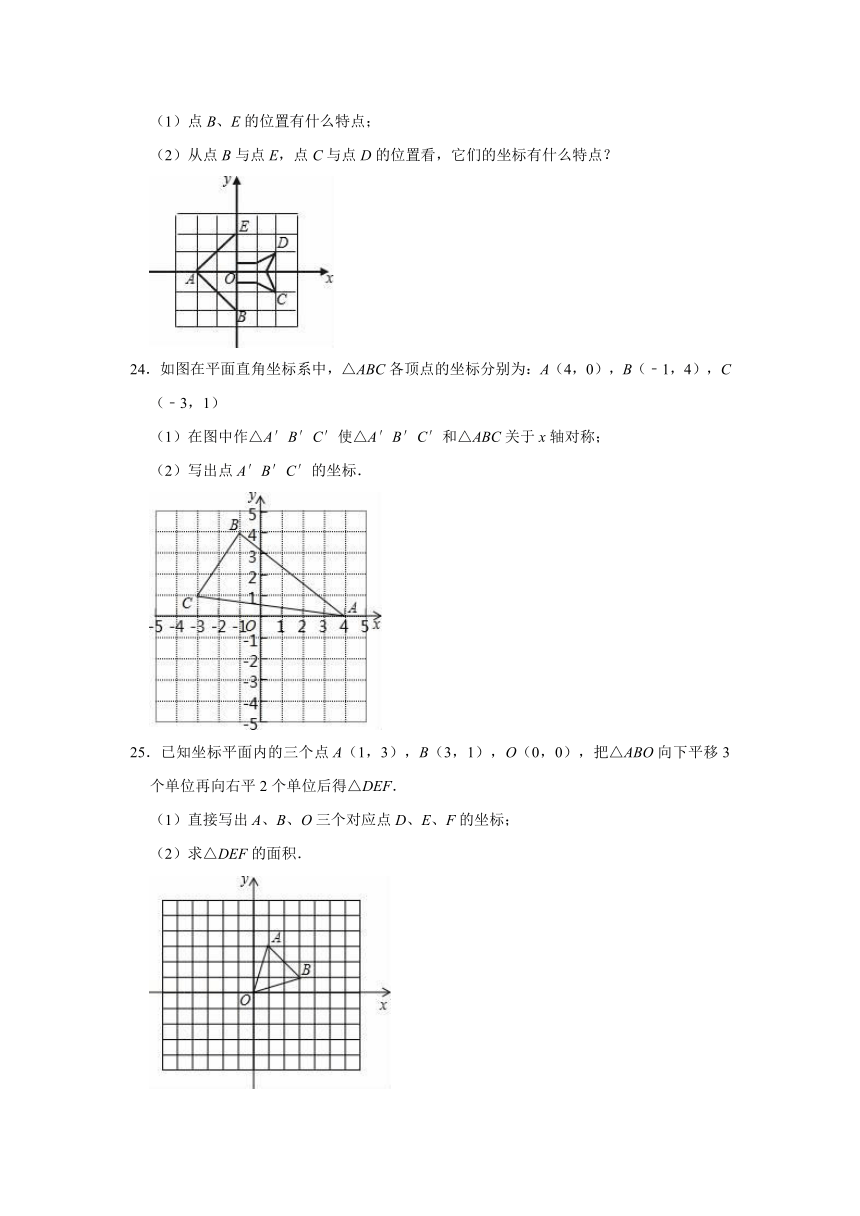
24.如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标.
25.已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),把△ABO向下平移3个单位再向右平2个单位后得△DEF.
(1)直接写出A、B、O三个对应点D、E、F的坐标;
(2)求△DEF的面积.
26.如图,已知单位长度为1的方格中有个△ABC.
(1)请画出△ABC向上平移3格再向右平移2格所得△A′B′C′.
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),
然后写出点B、点B′的坐标:B( , );B′( , )
2019年浙教新版八年级上册数学《第4章 图形与坐标》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.若x轴上的点P到y轴的距离是3,则点P的坐标为( )
A.(3,0) B.(3,0)或 (﹣3,0)
C.(3,0) D.(0,3)或 (0,﹣3)
【分析】根据x轴上点的纵坐标为0,点到y轴的距离等于横坐标的长度解答.
【解答】解:∵x轴上的点P到y轴的距离是3,
∴点P的横坐标为3或﹣3,纵坐标为0,
∴点P的坐标为(3,0)或 (﹣3,0).
故选:B.
【点评】本题考查了点的坐标,主要利用了x轴上点的坐标特征,要注意点的横坐标有两种情况.
2.如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第80秒时质点所在位置的坐标是( )
A.(0,9) B.(9,0) C.(0,8) D.( 8,0)
【分析】应先判断出走到坐标轴上的点所用的时间以及相对应的坐标,可发现走完一个正方形所用的时间分别为3,5,7,9…,此时点在坐标轴上,进而得到规律.
【解答】解:3秒时到了(1,0);
8秒时到了(0,2);
15秒时到了(3,0);
24秒到了(0,4);
35秒到了(5,0);
48秒到了(0,6);
63秒到了(7,0);
80秒到了(0,8).
∴第80秒时质点所在位置的坐标是(0,8).
故选:C.
【点评】本题是一个阅读理解,猜想规律的题目,解决问题的关键找到各点相对应的规律.
3.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(﹣3,3) B.(0,3) C.(3,2) D.(1,3)
【分析】根据棋子“馬”和“車”的点的坐标可得出原点的位置,进而得出答案.
【解答】解:如图所示:棋子“炮”的点的坐标为:(1,3).
故选:D.
【点评】此题主要考查了坐标确定位置,正确得出原点的位置是解题关键.
4.如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(﹣a,b),则点D的坐标为( )
A.(1,3) B.(3,﹣1) C.(﹣1,﹣3) D.(﹣3,1)
【分析】由A、E两点的纵坐标相等而横坐标互为相反数知A、E两点关于y轴对称,结合图形知B、D两点也关于y轴对称,据此可得答案.
【解答】解:如图,由点A、E的坐标分别为(a,b)、(﹣a,b)知A、E两点关于y轴对称,
则B、D两点也关于y轴对称,
∵B(3,1),
∴D(﹣3,1),
故选:D.
【点评】本题主要考查坐标与图形的性质,熟练掌握关于坐标轴对称的点的坐标特点是解题的关键.
5.点(3,﹣1)到原点的距离为( )
A.2 B.3 C.1 D.
【分析】直接利用两点间的距离公式计算即可.
【解答】解:点(3,﹣1)到原点的距离==.
故选:D.
【点评】本题考查了两点间的距离公式:设有两点A(x1,y1),B(x2,y2),则这两点间的距离为AB=.
6.P(4,﹣3)关于x轴对称点的坐标是( )
A.(4,3) B.(﹣4,﹣3) C.(﹣4,3) D.(﹣3,4)
【分析】根据关于x轴对称的点,横坐标相同,纵坐标互为相反数解答.
【解答】解:P(4,﹣3)关于x轴对称点的坐标是(4,3).
故选:A.
【点评】本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
7.已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,则点A的对应点A′的坐标是( )
A.(﹣3,2) B.(3,2) C.(﹣3,﹣2) D.(3,﹣2)
【分析】让点A的横坐标为原来横坐标的相反数,纵坐标不变可得所求点的坐标.
【解答】解:∵A的坐标为(﹣3,2),
∴A关于y轴的对应点的坐标为(3,2).
故选:B.
【点评】考查图形的对称变换;用到的知识点为:两点关于y轴对称,纵坐标不变,横坐标互为相反数.
8.将点P(m+2,2m+4)向右平移1个单位长度得到点M,且点M在y轴上,那么点M的坐标是( )
A.(﹣2,0) B.(0,﹣2) C.(1,0) D.(0,1)
【分析】根据横坐标,右移加,左移减得到点M(m+2+1,2m+4),再根据y轴上的点横坐标为0可得m+3=0,算出m的值,可得点M的坐标.
【解答】解:∵将点P(m+2,2m+4)向右平移1个单位长度得到点M,
∴M(m+2+1,2m+4),即(m+3,2m+4),
∵点M在y轴上,
∴m+3=0,
解得:m=﹣3,
∴点M的坐标为(0,﹣2),
故选:B.
【点评】此题主要考查了坐标与图形变化﹣平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.掌握点的坐标的变化规律是解题的关键.同时考查了y轴上的点横坐标为0的特征.
9.点A(﹣3,﹣5)向右平移2个单位,再向下平移3个单位到点B,则点B的坐标为( )
A.(﹣5,﹣8) B.(﹣5,﹣2) C.(﹣1,﹣8) D.(﹣1,﹣2)
【分析】直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
【解答】解:原来点的横坐标是﹣3,纵坐标是﹣5,
向右平移2个单位,再向下平移3个单位得到点B,
则点B的横坐标是﹣3+2=﹣1,纵坐标为﹣5﹣3=﹣8.
即点B的坐标为(﹣1,﹣8).
故选:C.
【点评】本题主要考查了平移中点的变化规律:左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
10.已知点A(1,a)、点B(b,2)关于原点对称,则a+b的值为( )
A.1 B.3 C.﹣1 D.﹣3
【分析】根据关于原点对称的点的坐标特点可得a、b的值,进而得到答案.
【解答】解:∵点A(1,a)、点B(b,2)关于原点对称,
∴b=﹣1,a=﹣2,
a+b=﹣3,
故选:D.
【点评】此题主要考查了关于原点对称的点的坐标特点,关键是掌握两个点关于原点对称时,它们的坐标符号相反.
二.填空题(共8小题)
11.若点M(a﹣3,a+4)在x轴上,则点M的坐标是 (﹣7,0) .
【分析】根据x轴上的点纵坐标为0,列式求出a的值,然后计算求出横坐标,从而点M的坐标可得.
【解答】解:∵M(a﹣3,a+4)在x轴上,
∴a+4=0,
解得a=﹣4,
∴a﹣3=﹣4﹣3=﹣7,
∴M点的坐标为(﹣7,0).
故答案为(﹣7,0).
【点评】本题主要考查了点的坐标,利用x轴上的点纵坐标等于0列式求出a的值是解题的关键.
12.在平面直角坐标系中,点A1(1,1),A2(3,4),A3(5,9),A4(7,16),…,用你发现的规律确定A10的坐标为 (19,100) .
【分析】观察不难发现,横坐标是从1开始的连续奇数,纵坐标是相应序数的平方,根据此规律计算即可得解.
【解答】解:∵点A1(1,1),A2(3,4),A3(5,9),A4(7,16),…,
∴点A10的横坐标是2×10﹣1=19,
纵坐标是102=100,
∴A10的坐标(19,100).
故答案为:(19,100).
【点评】本题考查了点的坐标的变化规律问题,从横坐标与纵坐标两个方面考虑变化规律是解题的关键.
13.如图,若在象棋盘上建立平面直角坐标系xOy,使“帥”的坐标为(﹣1,﹣2),“馬”的坐标为(2,﹣2),则“兵”的坐标为 (﹣3,1) .
【分析】直接利用已知点坐标得出原点的位置进而得出答案.
【解答】解:如图所示:“兵”的坐标为:(﹣3,1).
故答案为:(﹣3,1).
【点评】此题主要考查了坐标确定位置,正确得出原点位置是解题关键.
14.已知线段MN平行于x轴,且MN的长度为5,若M(2,﹣2),则点N的坐标 (7,﹣2)或(﹣3,﹣2) .
【分析】根据平行于x轴的直线上点的纵坐标相同,再分点N在点M的坐左边和右边两种情况讨论求解.
【解答】解:MN平行于x轴,故N的纵坐标不变,是﹣2,
点N在点M的左边时,横坐标为2﹣5=﹣3,
点N在点M的右边时,横坐标为2+5=7,
所以,点N的坐标为(7,﹣2)或(﹣3,﹣2).
故答案为:(7,﹣2)或(﹣3,﹣2).
【点评】本题考查了坐标与图形性质,主要利用了平行于x轴的直线上点的纵坐标相同,难点在于要分情况讨论.
15.点A(2,﹣1)关于x轴的对称点A′的坐标是 (2,1) .
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得答案.
【解答】解:点A(2,﹣1)关于x轴的对称点A′的坐标是(2,1),
故答案为:(2,1).
【点评】此题主要考查了关于x轴对称的点的坐标,关键是掌握点的坐标的变化规律.
16.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2019次变换后所得的A点坐标是 (﹣a,b) .
【分析】观察图形可知每四次对称为一个循环组依次循环,用2019除以4,然后根据商和余数的情况确定出变换后的点A所在的象限,然后解答即可.
【解答】解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2019÷4=504余3,
∴经过第2019次变换后所得的A点与第三次变换的位置相同,在第二象限,坐标为(﹣a,b).
故答案为:(﹣a,b)
【点评】本题考查了轴对称的性质,点的坐标变换规律,读懂题目信息,观察出每四次对称为一个循环组依次循环是解题的关键,也是本题的难点.
17.如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为 (a+3,b+2) .
【分析】找到一对对应点的平移规律,让点P的坐标也做相应变化即可.
【解答】解:点B的坐标为(﹣2,0),点B′的坐标为(1,2);
横坐标增加了1﹣(﹣2)=3;纵坐标增加了2﹣0=2;
∵△ABC上点P的坐标为(a,b),
∴点P的横坐标为a+3,纵坐标为b+2,
∴点P变换后的对应点P′的坐标为(a+3,b+2).
【点评】解决本题的关键是根据已知对应点找到各对应点之间的变化规律.
18.将点P向下平移3个单位,向左平移2个单位后得到点Q(3,﹣1),则点P坐标为 (5,2) .
【分析】设点P的坐标为(x,y),然后根据向左平移,横坐标减,向下平移,纵坐标减,列式进行计算即可得解.
【解答】解:设点P的坐标为(x,y),
根据题意,x﹣2=3,y﹣3=﹣1,
解得x=5,y=2,
则点P的坐标为(5,2).
故答案为:(5,2).
【点评】本题考查了平移与坐标与图形的变化,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
三.解答题(共8小题)
19.已知:点P(2m+4,m﹣1).试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过A(2,﹣3)点,且与x轴平行的直线上.
【分析】(1)让横坐标为0求得m的值,代入点P的坐标即可求解;
(2)让纵坐标为0求得m的值,代入点P的坐标即可求解;
(3)让纵坐标﹣横坐标=3得m的值,代入点P的坐标即可求解;
(4)让纵坐标为﹣3求得m的值,代入点P的坐标即可求解;
【解答】解:(1)令2m+4=0,解得m=﹣2,所以P点的坐标为(0,﹣3);
(2)令m﹣1=0,解得m=1,所以P点的坐标为(6,0);
(3)令m﹣1=(2m+4)+3,解得m=﹣8,所以P点的坐标为(﹣12,﹣9);
(4)令m﹣1=﹣3,解得m=﹣2.所以P点的坐标为(0,﹣3).
【点评】用到的知识点为:y轴上的点的横坐标为0;x轴上的点的纵坐标为0;平行于x轴的直线上的点的纵坐标相等.
20.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.
(1)填写下列各点的坐标:
A1( 0 , 1 ),A3( 1 , 0 ),A12( 6 , 0 );
(2)写出点A4n的坐标(n是正整数):A4n( 2n , 0 );
(3)蚂蚁从点A2013到A2014的移动方向是 向右 .
【分析】(1)观察图形可知,在平面直角坐标系中可以直接找出答案;
(2)根据图中规律写出点A4n的坐标即可;
(3)根据2013÷4=503…1,可知从点A2013到点A2014的移动方向与从点A1到A2的方向一致.
【解答】解:(1)由图可知,
∴A1(0,1),A3(1,0),A12(6,0);
故答案为:0,1;1,0;6,0;
(2)由图可知:A4(2,0),A8(4,0),A12(6,0),
∴OA4n=4n÷2=2n,
∴点A4n的坐标(2n,0);
故答案为:2n,0;
(3)∵2013÷4=503…1,
∴从点A2013到点A2014的移动方向与从点A1到A2的方向一致为向右.
【点评】此题主要考查了点的变化规律,比较简单,仔细观察图形,确定出A4n都在x轴上是解题的关键.
21.如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
【分析】(1)根据点A的坐标为(0,3),即可建立正确的平面直角坐标系;
(2)观察建立的直角坐标系即可得出答案;
(3)分别作点A,B,C关于x轴的对称点A′,B′,C′,连接A′B′,B′C′,C′A′则△A′B′C′即为所求.
【解答】解:(1)所建立的平面直角坐标系如下所示:
(2)点B和点C的坐标分别为:B(﹣3,﹣1)C(1,1);
(3)所作△A'B'C'如下图所示.
【点评】本题考查了轴对称变换作图,作轴对称后的图形的依据是轴对称的性质,基本作法是:①先确定图形的关键点;②利用轴对称性质作出关键点的对称点;③按原图形中的方式顺次连接对称点.
22.对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 (7,﹣3) ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
【分析】(Ⅰ)根据“k属派生点”计算可得;
(Ⅱ)设点P的坐标为(x、y),根据“k属派生点”定义及P′的坐标列出关于x、y的方程组,解之可得;
(Ⅲ)先得出点P′的坐标为(a,ka),由线段PP′的长度为线段OP长度的2倍列出方程,解之可得.
【解答】解:(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为(﹣2+3×3,﹣2×3+3),即(7,﹣3),
故答案为:(7,﹣3);
(Ⅱ)设P(x,y),
依题意,得方程组:,
解得,
∴点P(﹣2,1).
(Ⅲ)∵点P(a,b)在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka),
∴线段PP′的长为点P′到x轴距离为|ka|,
∵P在x轴正半轴,线段OP的长为a,
根据题意,有|PP'|=2|OP|,
∴|ka|=2a,
∵a>0,
∴|k|=2.
从而k=±2.
【点评】本题主要考查坐标与图形的性质,熟练掌握新定义并列出相关的方程和方程组是解题的关键.
23.写出如图中“小鱼”上所标各点的坐标并回答:
(1)点B、E的位置有什么特点;
(2)从点B与点E,点C与点D的位置看,它们的坐标有什么特点?
【分析】根据图象可直观看出点B和点E在y轴上,且到x轴的距离都是2个单位长度所以它们关于x轴对称;点C与点D也是关于x轴对称,所以它们的横坐标相同纵坐标互为相反数.
【解答】解:(1)点B(0,﹣2)和点E(0,2)关于x轴对称;
(2)点B(0,﹣2)与点E(0,2),点C(2,﹣1)与点D(2,1),它们的横坐标相同纵坐标互为相反数.
【点评】主要考查了平面直角坐标系中对称点的规律.解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
24.如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标.
【分析】(1)根据关于x轴对称的点的坐标特征得到点A′的坐标为(4,0),点B′的坐标为(﹣1,﹣4),点C′的坐标为(﹣3,﹣1),然后描点;
(2)由(1)可得到三个对应点的坐标.
【解答】解:(1)如图,
(2)点A′的坐标为(4,0),点B′的坐标为(﹣1,﹣4),点C′的坐标为(﹣3,﹣1).
【点评】本题考查了关坐标与图形﹣对称:关于x轴对称:横坐标相等,纵坐标互为相反数;关于y轴对称:纵坐标相等,横坐标互为相反数.
25.已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),把△ABO向下平移3个单位再向右平2个单位后得△DEF.
(1)直接写出A、B、O三个对应点D、E、F的坐标;
(2)求△DEF的面积.
【分析】(1)根据点的平移规律:横坐标,右移加,左移减;纵坐标,上移加,下移减可以直接算出A、B、O三个对应点D、E、F的坐标;
(2)把△DEF放在一个矩形中,利用矩形的面积减去周围多余三角形的面积即可.
【解答】解:(1)∵点A(1,3),B(3,1),O(0,0),
∴把△ABO向下平移3个单位再向右平移2个单位后A、B、O三个对应点D(1+2,3﹣3)、E(3+2,1﹣3)、F(0+2,0﹣3),
即D(3,0)、E(5,﹣2)、F(2,﹣3);
(2)△DEF的面积:3×3﹣×1×3﹣×1×3﹣×2×2=4.
【点评】此题主要考查了坐标与图形的变化,关键是掌握平移后点的变化规律.
26.如图,已知单位长度为1的方格中有个△ABC.
(1)请画出△ABC向上平移3格再向右平移2格所得△A′B′C′.
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),
然后写出点B、点B′的坐标:B( 1 , 2 );B′( 3 , 5 )
【分析】(1)把3个顶点向上平移3个单位,再向右平移2个单位,顺次连接个顶点即可;
(2)以点A为坐标原点,建立平面直角坐标系,找到所求点的坐标即可.
【解答】解:(1)如图可得△A′B′C′.
(2)如上图,以点A为坐标原点建立平面直角坐标系,则B(1,2);B′(3,5).
【点评】在平面直角坐标系中,图形的平移与图形上某点的平移相同,注意上下移动改变点的纵坐标,下减,上加.
一.选择题(共10小题)
1.若x轴上的点P到y轴的距离是3,则点P的坐标为( )
A.(3,0) B.(3,0)或 (﹣3,0)
C.(3,0) D.(0,3)或 (0,﹣3)
2.如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第80秒时质点所在位置的坐标是( )
A.(0,9) B.(9,0) C.(0,8) D.( 8,0)
3.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(﹣3,3) B.(0,3) C.(3,2) D.(1,3)
4.如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(﹣a,b),则点D的坐标为( )
A.(1,3) B.(3,﹣1) C.(﹣1,﹣3) D.(﹣3,1)
5.点(3,﹣1)到原点的距离为( )
A.2 B.3 C.1 D.
6.P(4,﹣3)关于x轴对称点的坐标是( )
A.(4,3) B.(﹣4,﹣3) C.(﹣4,3) D.(﹣3,4)
7.已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,则点A的对应点A′的坐标是( )
A.(﹣3,2) B.(3,2) C.(﹣3,﹣2) D.(3,﹣2)
8.将点P(m+2,2m+4)向右平移1个单位长度得到点M,且点M在y轴上,那么点M的坐标是( )
A.(﹣2,0) B.(0,﹣2) C.(1,0) D.(0,1)
9.点A(﹣3,﹣5)向右平移2个单位,再向下平移3个单位到点B,则点B的坐标为( )
A.(﹣5,﹣8) B.(﹣5,﹣2) C.(﹣1,﹣8) D.(﹣1,﹣2)
10.已知点A(1,a)、点B(b,2)关于原点对称,则a+b的值为( )
A.1 B.3 C.﹣1 D.﹣3
二.填空题(共8小题)
11.若点M(a﹣3,a+4)在x轴上,则点M的坐标是 .
12.在平面直角坐标系中,点A1(1,1),A2(3,4),A3(5,9),A4(7,16),…,用你发现的规律确定A10的坐标为 .
13.如图,若在象棋盘上建立平面直角坐标系xOy,使“帥”的坐标为(﹣1,﹣2),“馬”的坐标为(2,﹣2),则“兵”的坐标为 .
14.已知线段MN平行于x轴,且MN的长度为5,若M(2,﹣2),则点N的坐标 .
15.点A(2,﹣1)关于x轴的对称点A′的坐标是 .
16.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2019次变换后所得的A点坐标是 .
17.如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为 .
18.将点P向下平移3个单位,向左平移2个单位后得到点Q(3,﹣1),则点P坐标为 .
三.解答题(共8小题)
19.已知:点P(2m+4,m﹣1).试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过A(2,﹣3)点,且与x轴平行的直线上.
20.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.
(1)填写下列各点的坐标:
A1( , ),A3( , ),A12( , );
(2)写出点A4n的坐标(n是正整数):A4n( , );
(3)蚂蚁从点A2013到A2014的移动方向是 .
21.如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
22.对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
23.写出如图中“小鱼”上所标各点的坐标并回答:
(1)点B、E的位置有什么特点;
(2)从点B与点E,点C与点D的位置看,它们的坐标有什么特点?
24.如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标.
25.已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),把△ABO向下平移3个单位再向右平2个单位后得△DEF.
(1)直接写出A、B、O三个对应点D、E、F的坐标;
(2)求△DEF的面积.
26.如图,已知单位长度为1的方格中有个△ABC.
(1)请画出△ABC向上平移3格再向右平移2格所得△A′B′C′.
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),
然后写出点B、点B′的坐标:B( , );B′( , )
2019年浙教新版八年级上册数学《第4章 图形与坐标》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.若x轴上的点P到y轴的距离是3,则点P的坐标为( )
A.(3,0) B.(3,0)或 (﹣3,0)
C.(3,0) D.(0,3)或 (0,﹣3)
【分析】根据x轴上点的纵坐标为0,点到y轴的距离等于横坐标的长度解答.
【解答】解:∵x轴上的点P到y轴的距离是3,
∴点P的横坐标为3或﹣3,纵坐标为0,
∴点P的坐标为(3,0)或 (﹣3,0).
故选:B.
【点评】本题考查了点的坐标,主要利用了x轴上点的坐标特征,要注意点的横坐标有两种情况.
2.如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第80秒时质点所在位置的坐标是( )
A.(0,9) B.(9,0) C.(0,8) D.( 8,0)
【分析】应先判断出走到坐标轴上的点所用的时间以及相对应的坐标,可发现走完一个正方形所用的时间分别为3,5,7,9…,此时点在坐标轴上,进而得到规律.
【解答】解:3秒时到了(1,0);
8秒时到了(0,2);
15秒时到了(3,0);
24秒到了(0,4);
35秒到了(5,0);
48秒到了(0,6);
63秒到了(7,0);
80秒到了(0,8).
∴第80秒时质点所在位置的坐标是(0,8).
故选:C.
【点评】本题是一个阅读理解,猜想规律的题目,解决问题的关键找到各点相对应的规律.
3.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(﹣3,3) B.(0,3) C.(3,2) D.(1,3)
【分析】根据棋子“馬”和“車”的点的坐标可得出原点的位置,进而得出答案.
【解答】解:如图所示:棋子“炮”的点的坐标为:(1,3).
故选:D.
【点评】此题主要考查了坐标确定位置,正确得出原点的位置是解题关键.
4.如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(﹣a,b),则点D的坐标为( )
A.(1,3) B.(3,﹣1) C.(﹣1,﹣3) D.(﹣3,1)
【分析】由A、E两点的纵坐标相等而横坐标互为相反数知A、E两点关于y轴对称,结合图形知B、D两点也关于y轴对称,据此可得答案.
【解答】解:如图,由点A、E的坐标分别为(a,b)、(﹣a,b)知A、E两点关于y轴对称,
则B、D两点也关于y轴对称,
∵B(3,1),
∴D(﹣3,1),
故选:D.
【点评】本题主要考查坐标与图形的性质,熟练掌握关于坐标轴对称的点的坐标特点是解题的关键.
5.点(3,﹣1)到原点的距离为( )
A.2 B.3 C.1 D.
【分析】直接利用两点间的距离公式计算即可.
【解答】解:点(3,﹣1)到原点的距离==.
故选:D.
【点评】本题考查了两点间的距离公式:设有两点A(x1,y1),B(x2,y2),则这两点间的距离为AB=.
6.P(4,﹣3)关于x轴对称点的坐标是( )
A.(4,3) B.(﹣4,﹣3) C.(﹣4,3) D.(﹣3,4)
【分析】根据关于x轴对称的点,横坐标相同,纵坐标互为相反数解答.
【解答】解:P(4,﹣3)关于x轴对称点的坐标是(4,3).
故选:A.
【点评】本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
7.已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,则点A的对应点A′的坐标是( )
A.(﹣3,2) B.(3,2) C.(﹣3,﹣2) D.(3,﹣2)
【分析】让点A的横坐标为原来横坐标的相反数,纵坐标不变可得所求点的坐标.
【解答】解:∵A的坐标为(﹣3,2),
∴A关于y轴的对应点的坐标为(3,2).
故选:B.
【点评】考查图形的对称变换;用到的知识点为:两点关于y轴对称,纵坐标不变,横坐标互为相反数.
8.将点P(m+2,2m+4)向右平移1个单位长度得到点M,且点M在y轴上,那么点M的坐标是( )
A.(﹣2,0) B.(0,﹣2) C.(1,0) D.(0,1)
【分析】根据横坐标,右移加,左移减得到点M(m+2+1,2m+4),再根据y轴上的点横坐标为0可得m+3=0,算出m的值,可得点M的坐标.
【解答】解:∵将点P(m+2,2m+4)向右平移1个单位长度得到点M,
∴M(m+2+1,2m+4),即(m+3,2m+4),
∵点M在y轴上,
∴m+3=0,
解得:m=﹣3,
∴点M的坐标为(0,﹣2),
故选:B.
【点评】此题主要考查了坐标与图形变化﹣平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.掌握点的坐标的变化规律是解题的关键.同时考查了y轴上的点横坐标为0的特征.
9.点A(﹣3,﹣5)向右平移2个单位,再向下平移3个单位到点B,则点B的坐标为( )
A.(﹣5,﹣8) B.(﹣5,﹣2) C.(﹣1,﹣8) D.(﹣1,﹣2)
【分析】直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
【解答】解:原来点的横坐标是﹣3,纵坐标是﹣5,
向右平移2个单位,再向下平移3个单位得到点B,
则点B的横坐标是﹣3+2=﹣1,纵坐标为﹣5﹣3=﹣8.
即点B的坐标为(﹣1,﹣8).
故选:C.
【点评】本题主要考查了平移中点的变化规律:左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
10.已知点A(1,a)、点B(b,2)关于原点对称,则a+b的值为( )
A.1 B.3 C.﹣1 D.﹣3
【分析】根据关于原点对称的点的坐标特点可得a、b的值,进而得到答案.
【解答】解:∵点A(1,a)、点B(b,2)关于原点对称,
∴b=﹣1,a=﹣2,
a+b=﹣3,
故选:D.
【点评】此题主要考查了关于原点对称的点的坐标特点,关键是掌握两个点关于原点对称时,它们的坐标符号相反.
二.填空题(共8小题)
11.若点M(a﹣3,a+4)在x轴上,则点M的坐标是 (﹣7,0) .
【分析】根据x轴上的点纵坐标为0,列式求出a的值,然后计算求出横坐标,从而点M的坐标可得.
【解答】解:∵M(a﹣3,a+4)在x轴上,
∴a+4=0,
解得a=﹣4,
∴a﹣3=﹣4﹣3=﹣7,
∴M点的坐标为(﹣7,0).
故答案为(﹣7,0).
【点评】本题主要考查了点的坐标,利用x轴上的点纵坐标等于0列式求出a的值是解题的关键.
12.在平面直角坐标系中,点A1(1,1),A2(3,4),A3(5,9),A4(7,16),…,用你发现的规律确定A10的坐标为 (19,100) .
【分析】观察不难发现,横坐标是从1开始的连续奇数,纵坐标是相应序数的平方,根据此规律计算即可得解.
【解答】解:∵点A1(1,1),A2(3,4),A3(5,9),A4(7,16),…,
∴点A10的横坐标是2×10﹣1=19,
纵坐标是102=100,
∴A10的坐标(19,100).
故答案为:(19,100).
【点评】本题考查了点的坐标的变化规律问题,从横坐标与纵坐标两个方面考虑变化规律是解题的关键.
13.如图,若在象棋盘上建立平面直角坐标系xOy,使“帥”的坐标为(﹣1,﹣2),“馬”的坐标为(2,﹣2),则“兵”的坐标为 (﹣3,1) .
【分析】直接利用已知点坐标得出原点的位置进而得出答案.
【解答】解:如图所示:“兵”的坐标为:(﹣3,1).
故答案为:(﹣3,1).
【点评】此题主要考查了坐标确定位置,正确得出原点位置是解题关键.
14.已知线段MN平行于x轴,且MN的长度为5,若M(2,﹣2),则点N的坐标 (7,﹣2)或(﹣3,﹣2) .
【分析】根据平行于x轴的直线上点的纵坐标相同,再分点N在点M的坐左边和右边两种情况讨论求解.
【解答】解:MN平行于x轴,故N的纵坐标不变,是﹣2,
点N在点M的左边时,横坐标为2﹣5=﹣3,
点N在点M的右边时,横坐标为2+5=7,
所以,点N的坐标为(7,﹣2)或(﹣3,﹣2).
故答案为:(7,﹣2)或(﹣3,﹣2).
【点评】本题考查了坐标与图形性质,主要利用了平行于x轴的直线上点的纵坐标相同,难点在于要分情况讨论.
15.点A(2,﹣1)关于x轴的对称点A′的坐标是 (2,1) .
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得答案.
【解答】解:点A(2,﹣1)关于x轴的对称点A′的坐标是(2,1),
故答案为:(2,1).
【点评】此题主要考查了关于x轴对称的点的坐标,关键是掌握点的坐标的变化规律.
16.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2019次变换后所得的A点坐标是 (﹣a,b) .
【分析】观察图形可知每四次对称为一个循环组依次循环,用2019除以4,然后根据商和余数的情况确定出变换后的点A所在的象限,然后解答即可.
【解答】解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2019÷4=504余3,
∴经过第2019次变换后所得的A点与第三次变换的位置相同,在第二象限,坐标为(﹣a,b).
故答案为:(﹣a,b)
【点评】本题考查了轴对称的性质,点的坐标变换规律,读懂题目信息,观察出每四次对称为一个循环组依次循环是解题的关键,也是本题的难点.
17.如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为 (a+3,b+2) .
【分析】找到一对对应点的平移规律,让点P的坐标也做相应变化即可.
【解答】解:点B的坐标为(﹣2,0),点B′的坐标为(1,2);
横坐标增加了1﹣(﹣2)=3;纵坐标增加了2﹣0=2;
∵△ABC上点P的坐标为(a,b),
∴点P的横坐标为a+3,纵坐标为b+2,
∴点P变换后的对应点P′的坐标为(a+3,b+2).
【点评】解决本题的关键是根据已知对应点找到各对应点之间的变化规律.
18.将点P向下平移3个单位,向左平移2个单位后得到点Q(3,﹣1),则点P坐标为 (5,2) .
【分析】设点P的坐标为(x,y),然后根据向左平移,横坐标减,向下平移,纵坐标减,列式进行计算即可得解.
【解答】解:设点P的坐标为(x,y),
根据题意,x﹣2=3,y﹣3=﹣1,
解得x=5,y=2,
则点P的坐标为(5,2).
故答案为:(5,2).
【点评】本题考查了平移与坐标与图形的变化,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
三.解答题(共8小题)
19.已知:点P(2m+4,m﹣1).试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过A(2,﹣3)点,且与x轴平行的直线上.
【分析】(1)让横坐标为0求得m的值,代入点P的坐标即可求解;
(2)让纵坐标为0求得m的值,代入点P的坐标即可求解;
(3)让纵坐标﹣横坐标=3得m的值,代入点P的坐标即可求解;
(4)让纵坐标为﹣3求得m的值,代入点P的坐标即可求解;
【解答】解:(1)令2m+4=0,解得m=﹣2,所以P点的坐标为(0,﹣3);
(2)令m﹣1=0,解得m=1,所以P点的坐标为(6,0);
(3)令m﹣1=(2m+4)+3,解得m=﹣8,所以P点的坐标为(﹣12,﹣9);
(4)令m﹣1=﹣3,解得m=﹣2.所以P点的坐标为(0,﹣3).
【点评】用到的知识点为:y轴上的点的横坐标为0;x轴上的点的纵坐标为0;平行于x轴的直线上的点的纵坐标相等.
20.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.
(1)填写下列各点的坐标:
A1( 0 , 1 ),A3( 1 , 0 ),A12( 6 , 0 );
(2)写出点A4n的坐标(n是正整数):A4n( 2n , 0 );
(3)蚂蚁从点A2013到A2014的移动方向是 向右 .
【分析】(1)观察图形可知,在平面直角坐标系中可以直接找出答案;
(2)根据图中规律写出点A4n的坐标即可;
(3)根据2013÷4=503…1,可知从点A2013到点A2014的移动方向与从点A1到A2的方向一致.
【解答】解:(1)由图可知,
∴A1(0,1),A3(1,0),A12(6,0);
故答案为:0,1;1,0;6,0;
(2)由图可知:A4(2,0),A8(4,0),A12(6,0),
∴OA4n=4n÷2=2n,
∴点A4n的坐标(2n,0);
故答案为:2n,0;
(3)∵2013÷4=503…1,
∴从点A2013到点A2014的移动方向与从点A1到A2的方向一致为向右.
【点评】此题主要考查了点的变化规律,比较简单,仔细观察图形,确定出A4n都在x轴上是解题的关键.
21.如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
【分析】(1)根据点A的坐标为(0,3),即可建立正确的平面直角坐标系;
(2)观察建立的直角坐标系即可得出答案;
(3)分别作点A,B,C关于x轴的对称点A′,B′,C′,连接A′B′,B′C′,C′A′则△A′B′C′即为所求.
【解答】解:(1)所建立的平面直角坐标系如下所示:
(2)点B和点C的坐标分别为:B(﹣3,﹣1)C(1,1);
(3)所作△A'B'C'如下图所示.
【点评】本题考查了轴对称变换作图,作轴对称后的图形的依据是轴对称的性质,基本作法是:①先确定图形的关键点;②利用轴对称性质作出关键点的对称点;③按原图形中的方式顺次连接对称点.
22.对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 (7,﹣3) ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
【分析】(Ⅰ)根据“k属派生点”计算可得;
(Ⅱ)设点P的坐标为(x、y),根据“k属派生点”定义及P′的坐标列出关于x、y的方程组,解之可得;
(Ⅲ)先得出点P′的坐标为(a,ka),由线段PP′的长度为线段OP长度的2倍列出方程,解之可得.
【解答】解:(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为(﹣2+3×3,﹣2×3+3),即(7,﹣3),
故答案为:(7,﹣3);
(Ⅱ)设P(x,y),
依题意,得方程组:,
解得,
∴点P(﹣2,1).
(Ⅲ)∵点P(a,b)在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka),
∴线段PP′的长为点P′到x轴距离为|ka|,
∵P在x轴正半轴,线段OP的长为a,
根据题意,有|PP'|=2|OP|,
∴|ka|=2a,
∵a>0,
∴|k|=2.
从而k=±2.
【点评】本题主要考查坐标与图形的性质,熟练掌握新定义并列出相关的方程和方程组是解题的关键.
23.写出如图中“小鱼”上所标各点的坐标并回答:
(1)点B、E的位置有什么特点;
(2)从点B与点E,点C与点D的位置看,它们的坐标有什么特点?
【分析】根据图象可直观看出点B和点E在y轴上,且到x轴的距离都是2个单位长度所以它们关于x轴对称;点C与点D也是关于x轴对称,所以它们的横坐标相同纵坐标互为相反数.
【解答】解:(1)点B(0,﹣2)和点E(0,2)关于x轴对称;
(2)点B(0,﹣2)与点E(0,2),点C(2,﹣1)与点D(2,1),它们的横坐标相同纵坐标互为相反数.
【点评】主要考查了平面直角坐标系中对称点的规律.解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
24.如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标.
【分析】(1)根据关于x轴对称的点的坐标特征得到点A′的坐标为(4,0),点B′的坐标为(﹣1,﹣4),点C′的坐标为(﹣3,﹣1),然后描点;
(2)由(1)可得到三个对应点的坐标.
【解答】解:(1)如图,
(2)点A′的坐标为(4,0),点B′的坐标为(﹣1,﹣4),点C′的坐标为(﹣3,﹣1).
【点评】本题考查了关坐标与图形﹣对称:关于x轴对称:横坐标相等,纵坐标互为相反数;关于y轴对称:纵坐标相等,横坐标互为相反数.
25.已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),把△ABO向下平移3个单位再向右平2个单位后得△DEF.
(1)直接写出A、B、O三个对应点D、E、F的坐标;
(2)求△DEF的面积.
【分析】(1)根据点的平移规律:横坐标,右移加,左移减;纵坐标,上移加,下移减可以直接算出A、B、O三个对应点D、E、F的坐标;
(2)把△DEF放在一个矩形中,利用矩形的面积减去周围多余三角形的面积即可.
【解答】解:(1)∵点A(1,3),B(3,1),O(0,0),
∴把△ABO向下平移3个单位再向右平移2个单位后A、B、O三个对应点D(1+2,3﹣3)、E(3+2,1﹣3)、F(0+2,0﹣3),
即D(3,0)、E(5,﹣2)、F(2,﹣3);
(2)△DEF的面积:3×3﹣×1×3﹣×1×3﹣×2×2=4.
【点评】此题主要考查了坐标与图形的变化,关键是掌握平移后点的变化规律.
26.如图,已知单位长度为1的方格中有个△ABC.
(1)请画出△ABC向上平移3格再向右平移2格所得△A′B′C′.
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),
然后写出点B、点B′的坐标:B( 1 , 2 );B′( 3 , 5 )
【分析】(1)把3个顶点向上平移3个单位,再向右平移2个单位,顺次连接个顶点即可;
(2)以点A为坐标原点,建立平面直角坐标系,找到所求点的坐标即可.
【解答】解:(1)如图可得△A′B′C′.
(2)如上图,以点A为坐标原点建立平面直角坐标系,则B(1,2);B′(3,5).
【点评】在平面直角坐标系中,图形的平移与图形上某点的平移相同,注意上下移动改变点的纵坐标,下减,上加.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
