浙教版八年级数学上册教案1.4全等三角形(一)
文档属性
| 名称 | 浙教版八年级数学上册教案1.4全等三角形(一) |

|
|
| 格式 | zip | ||
| 文件大小 | 265.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-30 14:11:26 | ||
图片预览



文档简介
全等三角形(一)
教学目标
1.了解全等图形的概念,会用定义判定两个图形全等。
2.了解全等三角形的概念,理解全等三角形的对应边相等,对应角相等。
3.掌握SSS及SAS判定两个三角形全等
知识点一、全等图形及全等三角形
仔细观察下列各组图形,你发现了什么?
全等图形:能够重合的两个图形称为全等图形。
全等三角形:能够重合的两个三角形叫做全等三角形。
表示:△ABC≌△DEF
对应顶点:能互相重合的顶点叫全等三角形的对应顶点。
对应边:能互相重合的边叫全等三角形的对应边。
对应角:能互相重合的角叫做全等三角形的对应角。
面积相等的三角形是否是全等三角形?
【例题】
1、如图所示的图形是全等图形的是( )
A.B.C.D.
2、下列各组的两个图形属于全等图形的是?( )
A.B.C.D.
【课堂练习】
1、下列四个图形中,属于全等图形的是( )
A.①和② B.②和③ C.①和③ D.②和④
2、下列各图形中,不是全等形的是( )
A.B.C.D.
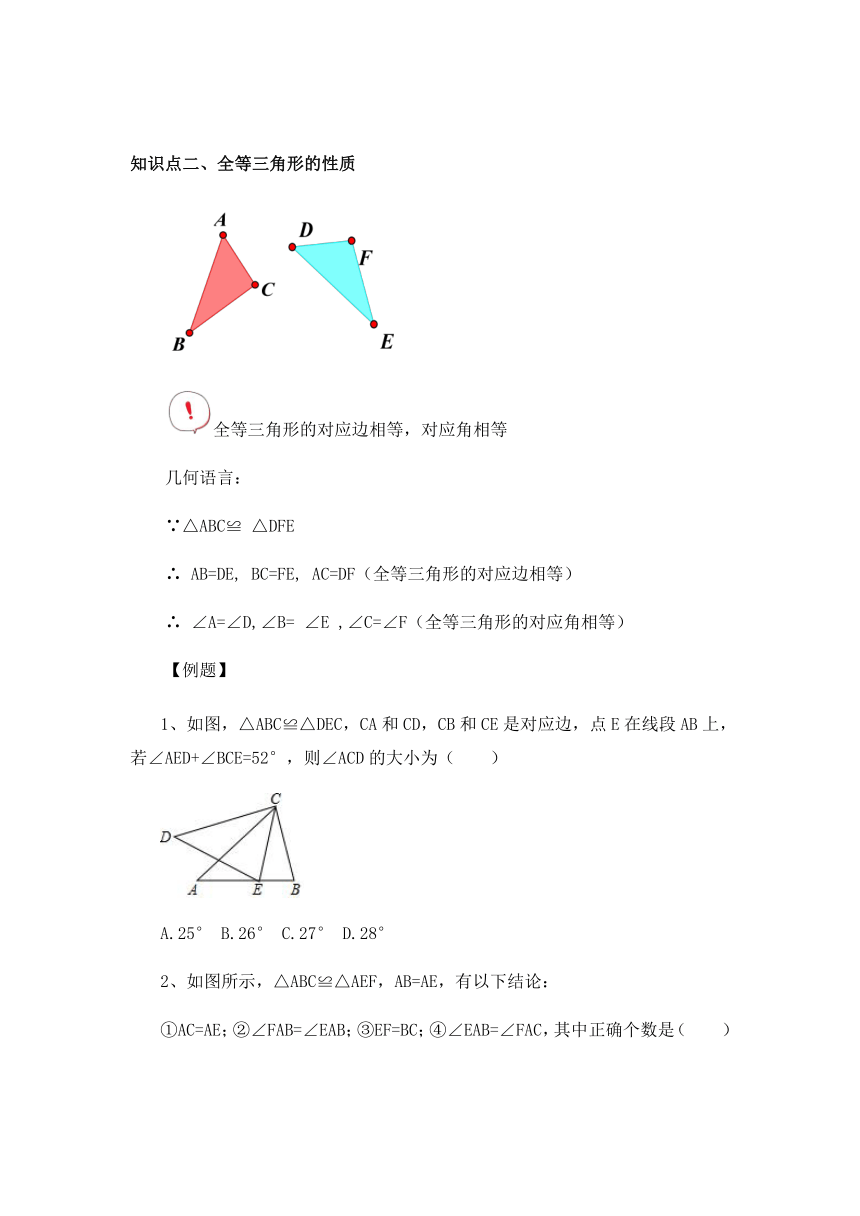
知识点二、全等三角形的性质
全等三角形的对应边相等,对应角相等
几何语言:
∵△ABC≌ △DFE
∴ AB=DE, BC=FE, AC=DF(全等三角形的对应边相等)
∴ ∠A=∠D,∠B= ∠E ,∠C=∠F(全等三角形的对应角相等)
【例题】
1、如图,△ABC≌△DEC,CA和CD,CB和CE是对应边,点E在线段AB上,若∠AED+∠BCE=52°,则∠ACD的大小为( )
A.25° B.26° C.27° D.28°
2、如图所示,△ABC≌△AEF,AB=AE,有以下结论:
①AC=AE;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确个数是( )
A.1 B.2 C.3 D.4
3、已知:△ABC≌△DCB,若BC=10cm,AB=5cm,AC=7cm,则CD为( )
A.10cm B.7cm C.5cm D.5cm或7cm
【课堂练习】
1、如图,△ABC≌△ADE,点A,B,E在同一直线上,∠B=20°,∠BAD=50°,则∠C的度数为( )
A.20° B.30° C.40° D.50°
2、若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
A.5 B.8 C.7 D.5或8
3、若△ABC≌△DEF,若BE=2,则CF的长为( )
A.2 B.3 C.4 D.5
知识点三、全等三角形判定
1、SSS
知一个三角形的三条边分别为4cm,5cm,7cm,你能画出这个三角形吗?
画法:画线段AB=5cm;
分别以A、B为圆心,4cm和7cm长为半径画两条圆弧,交于点C;
连结AC、BC;
△ABC就是所求的三角形。
三条边分别为4cm,5cm,7cm只有这一种吗,还能不能画出其他三角形?
有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
几何语言(五行法):
在△ABC和△DEF中
AB=DE(已知)
BC=DF(已知)
AC=DF(已知)
∴△ABC≌ △DFE(SSS)
【例题】
1、如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
【课堂练习】
1、如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACEC.△BDE≌△CDE D.以上答案都不对
2、SAS
让我们动手做一做:用量角器和刻度尺画ΔABC,使 AB=4cm,BC=6cm,
∠ABC=60°,将你画出的三角形和其他同学画的三角形进行比较,它们互相
重合吗?
有两边及两边的夹角对应相等的两个三角形全等(简写成“边角边”
或“SAS”)
几何语言(五行法):
在△ABC和△DEF中
AC=DF(已知)
∠ACB=∠DFE(已知)
BC=DF(已知)
∴△ABC≌ △DFE(SAS)
【例题】
1、如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
A.AC=DF B.BE=CF C.∠A=∠D D.∠ACB=∠DFE
2、已知,如图,AB=CD,AB∥CD,BE=FD,问△ABF与△CDE全等吗?
【课堂练习】
1、如图,AC与BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )
A.AB=DC B.OB=OC C.∠A=∠D D.∠AOB=∠DOC
2、如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )
A.AD=BC B.BD=AC C.∠D=∠C D.OA=AB
3、如图,已知AC平分∠BAD,AB=AD.求证:△ABC≌△ADC.
4、如图,D、E分别是AB、AC上的点,且AB=AC,AD=AE.
求证:∠B=∠C.
课堂总结
1.全等三角形的对应边相等,对应角相等
2.有三边对应相等的两个三角形全等
3.有两边及两边的夹角对应相等的两个三角形全等
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
