第四章 平行四边形单元测试卷（含解析）

中小学教育资源及组卷应用平台
浙教版2019-2020八年级数学下册第四章平行四边形单元测试卷解析版
一、选择题（每小题3分，共30分）
1.我国传统文化中的“福禄寿喜”图(如图)由四个图案构成，这四个图案中是中心对称图形的是(
)
A. B. C. D.
2.从九边形的一个顶点出发可以引出的对角线条数为（
）
A. 3 B. 4 C. 6 D. 9
3.一个四边形，截一刀后得到新多边形的内角和将（
）
A. 增加180° B. 减少180° C. 不变 D. 以上三种情况都有可能
4.已知一个多边形的内角和为540°,则这个多边形为（
）
A. 三角形 B. 四边形 C. 五边形 D. 六边形
5.一个多边形的内角和等于它的外角和，则它的内角和等于（
）
A. 360° B. 540° C. 720° D. 1080°
6.如图，在 ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于
（
）
A. 1cm B. 2cm C. 3cm D. 4cm
7.如图，七边形
中，
、
的延长线相交于点
，若图中
、
、
、
的外角和为
，则
的度数为(
)
A. B. C. D.
8.用反证法证明命题“在同一平面内，如果两条直线都和第三条直线平行，那么这两条直线互相平行”，第一步应假设(
)
A. 这两条直线互相垂直 B. 这两条直线互相平行 C. 这两条直线不平行 D. 这两条直线不垂直
9.如图，△ABC中，点D、E分别在AB、AC边上，AD=BD，AE=EC，BC=6，则DE=（
）
A. 4 B. 3 C. 2 D. 5
10.如图①，在△ABC中，D，E分别是AB，AC的中点把△ADE沿线段DE向下折叠，使点A落在BC上的点A'处，得到图②，则下列四个结论中，不一定成立的是(
)
A. DB=DA B. ∠B+∠C+∠1=180° C. △ADE≌△A'DE D. BA=CA
二、填空题（每小题3分，共18分）
11.八边形从其中的任何一个顶点最多可画________条对角线，这些对角线可将八边形分成________三角形.
12.如图,在四边形ABCD中,已知AB∥CD,再添加一个条件________,则四边形ABCD是平行四边形(图中不再添加辅助线)
13.如图，在△ABC中，已知AB=8，
BC=5，点D，E分别为BC、AC的中点，BF平分∠ABC交DE于点F，则EF的长为________ 。
14.如图，A、B两处被池塘隔开，为了测量A、B两处的距离，在AB外选适当的点C，连结AC、BC，并分别取线段AC、BC的中点E、F，测得EF=22m，则AB=________m．
15.如图，已知在
中，
，点
是
延长线上的一点，
，点
是
上一点，
，连接
，
、
分别是
、
的中点，则
________.
16.如图，在平行四边形ABCD中，AB＝2AD
，
BE平分∠ABC交CD于点E
，
作BF⊥AD
，
垂足为F
，
连接EF
，
小明得到三个结论：①∠FBC＝90°；②ED＝EB；③S△EBF＝S△EDF+S△EBC；则三个结论中一定成立的是________．
三、解答题（共8题；共52分）
17.如图，在平行四边形ABCD中，点E，F分别在AB，CD上，AE=CF.
求证：DE=BF.
18.如图，五边形
ABCDE中，AE∥CD，∠A=107°，∠B=121°，求∠C的度数。
19.如图，在平行四边形ABCD
中，
于
，
于
，连接
，
.求证：四边形
是平行四边形.
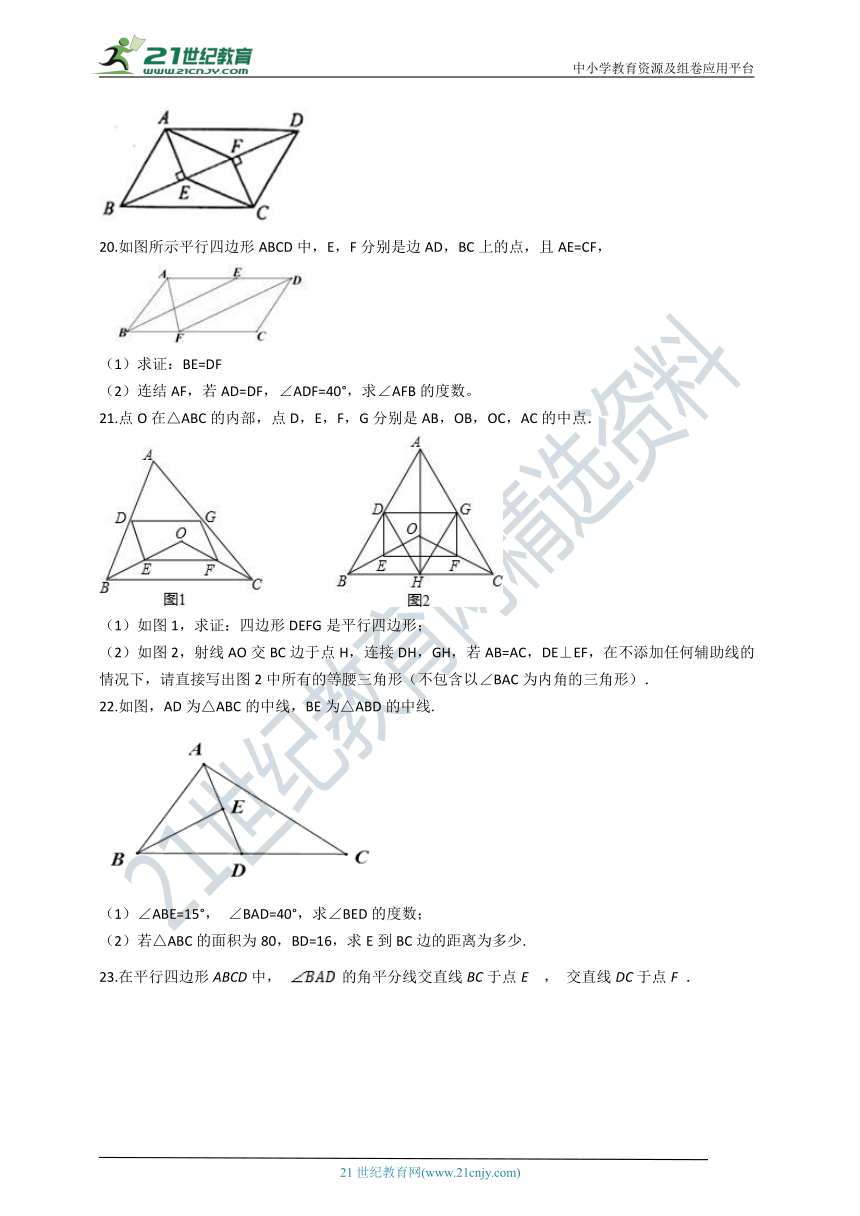
20.如图所示平行四边形ABCD中，E，F分别是边AD，BC上的点，且AE=CF，
（1）求证：BE=DF
（2）连结AF，若AD=DF，∠ADF=40°，求∠AFB的度数。
21.点O在△ABC的内部，点D，E，F，G分别是AB，OB，OC，AC的中点．
（1）如图1，求证：四边形DEFG是平行四边形；
（2）如图2，射线AO交BC边于点H，连接DH，GH，若AB=AC，DE⊥EF，在不添加任何辅助线的情况下，请直接写出图2中所有的等腰三角形（不包含以∠BAC为内角的三角形）．
22.如图，AD为△ABC的中线，BE为△ABD的中线.
（1）∠ABE=15°，
∠BAD=40°，求∠BED的度数；
（2）若△ABC的面积为80，BD=16，求E到BC边的距离为多少.
23.在平行四边形ABCD中，
的角平分线交直线BC于点E
，
交直线DC于点F
．
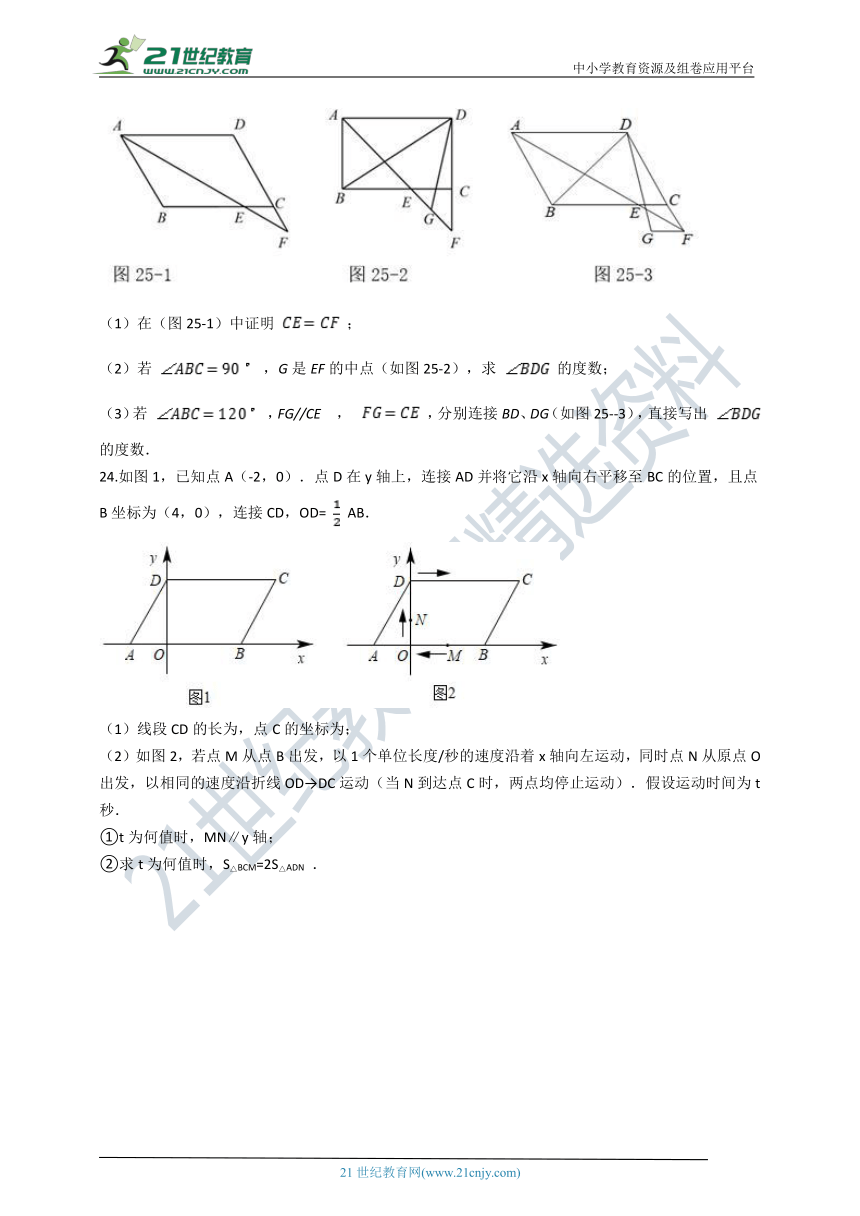
（1）在（图25-1）中证明
；
（2）若
，G是EF的中点（如图25-2），求
的度数；
（3）若
，FG//CE
，
，分别连接BD、DG（如图25--3），直接写出
的度数．
24.如图1，已知点A（-2，0）．点D在y轴上，连接AD并将它沿x轴向右平移至BC的位置，且点B坐标为（4，0），连接CD，OD=
AB．
（1）线段CD的长为，点C的坐标为；
（2）如图2，若点M从点B出发，以1个单位长度/秒的速度沿着x轴向左运动，同时点N从原点O出发，以相同的速度沿折线OD→DC运动（当N到达点C时，两点均停止运动）．假设运动时间为t秒．
①t为何值时，MN∥y轴；
②求t为何值时，S△BCM=2S△ADN
．
浙教版2019-2020八年级数学下册第四章平行四边形单元测试卷解析版
一、选择题（30分）
1.解：A．不是中心对称图形，不符合题意；
B．是中心对称图形，符合题意；
C．不是中心对称图形，不符合题意；
D．不是中心对称图形，不符合题意.
故答案为：B.
2.从九边形的一个顶点出发，可以向与这个顶点不相邻的6个顶点引对角线，即能引出6条对角线.
3.解：∵一个四边形截一刀后得到的多边形可能是三角形，可能是四边形，也可能是五边形，
∴内角和可能减少180°，可能不变，可能增加180°.
故答案为：D.
4.解：根据多边形的内角和可得：（n-2）180°=540°，
解得：n=5，则这个多边形是五边形.
故答案为：C.
5.解：∵任一多边形的外角和都为360，
∴此多边形的内角和为360°，
故答案为：A.
6.解：如图，
∵AE平分∠BAD交BC边于点E，
∴∠BAE=∠EAD，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC=5，
∴∠DAE=∠AEB，
∴∠BAE=∠AEB，
∴AB=BE=3，
∴EC=BC-BE=5-3=2.
故答案为：B.
7.在DO延长线上找一点M，如图所示.

∵多边形的外角和为360°，
∴∠BOM＝360° 240°＝120°.
∵∠BOD＋∠BOM＝180°，
∴∠BOD＝180° ∠BOM＝180° 120°＝60°.
故答案为：D.
8. 解：两条直线互相平行的反面应是两条直线不平行，同一平面内不平行有重合和
相交两种情况，其中相交包含垂直。
故答案为：C
9.∵AD=BD，AE=EC，
∴DE是△ABC的中位线，
∴BC=2DE，
∴DE=3，
故答案为：B．
10.解：如图，
A、∵
D，E分别是AB，AC的中点 ，∴DE是三角形ABC的中位线,
∴DE∥BC，∵DE⊥AA'，∴AA'⊥BC，
∴AD=BD=AD，正确，符合题意
;
B、∵∠A+∠B+∠C=180°，∠B+∠1+∠C=180
，
正确，不符合题意；
C、
△A'DE是由△ADE折叠而来，∴
△ADE≌△A'DE ，正确，不符合题意；
D、
△ABC是任意三角形，
由题意无法推出BA=CA，∴BA不一定等于CA，错误，符合题意.
故答案为：D.
二、填空题（18分）
11.解：八边形从其中的任何一个顶点最多可画8-3＝5条对角线；这些对角线可将八边形分成8-2＝6个三角形，
故答案为：5，6.
12.解：已知AB∥CD，
∵一组对边平行且相等的四边形是平行四边形；两组对边分别平行的四边形是平行四边形，
∴可添加AB=CD或AD∥BC，
故答案为：AB=CD（或AD∥BC）.
13.解：∵
D，E分别为BC、AC的中点，
∴DE=AB=×8=4，DE∥AB，
∵BF平分
∠ABC
，
∴
∠ABF=
∠CBF，
∵DE∥AB，
∴
∠ABF=
∠BFD，
∴DF=BD=2.5，
∴EF=DE-DF=4-2.5=1.5，
故答案为：1.5.
14.解：∵在△ABC中，E、F分别为CA、CB的中点，
∴EF是△ABC的中位线，
∴AB=2EF=44m
.
故答案为：
44
15.连接
，取
的中点
，连接
，
，
∵
、
分别是
、
的中点，
∴OM=
BE,ON=
AD,
∴
，
，
∵
、
分别是
、
的中点，
的中点
，
∴OM∥EB,ON∥AD,且
，
∴∠MON=90°，
由勾股定理，
.
故答案为：13.
16.解：∵BF⊥AD
，
∴∠AFB＝90°，
∵在平行四边形ABCD中，AD∥BC
，
∴∠AFB＝∠CBF＝90°，故①正确；
延长FE交BC的延长线与M
，
∴∠DFE＝∠M
，
在△DFE与△CME中，
，
∴△DFE≌△CME（AAS），
∴EF＝EM＝
FM
，
∵∠FBM＝90°，
∴BE＝
FM
，
∴EF＝BE
，
∵EF≠DE
，
故②错误；
∵EF＝EM
，
∴S△BEF＝S△BME
，
∵△DFE≌△CME
，
∴S△DFE＝S△CME
，
∴S△EBF＝S△BME＝S△EDF+S△EBC
．
故③正确．
故答案为：①③．
三、解答题（52分）
17.
证明：∵四边形ABCD是平行四边形，
∴AD=BC，∠A=∠C，
在△ADE和△CBF中，
，
∴△ADE≌△CBF（SAS），
∴DE=BF.
18.
解：五边形ABCDE的内角和为
即∠A+∠B+∠C+∠D+∠E=540°
∵AE∥CD，∴∠D+∠E=180°
∵∠A=107°，∠B=121°
∴∠C=132°
19.
证明：如图，
∵四边形
是平行四边形，
∴
，
∴
.
又∵
，
，
∴
，
.
∴
（AAS）.
∴
.
又
∴四边形
是平行四边形.
20.
（1）证明：∵平行四边形ABCD，
∴AD∥BC，AD=BC，
∵AE=CF
∴DE=BF，
∴四边形DEBF是平行四边形，
∴BE=DF.
（2）解：∵AD=DF
∴∠DAF=∠AFD
∵∠ADF=40°，
∴∠DAF=（180°-40°）÷2=70°，
∵AD∥BC，
∴∠AFB=∠DAF=70°.
21.
（1）证明：如图1中，
∵AD=DB，AG=GC，
∴DG∥BC，DG=
BC，
∵OE=EB，OF=FC，
∴EF∥BC，EF=
BC，
∴DG∥EF，EF=DG，
∴四边形DEFG是平行四边形．
（2）解：如图2中，
∵BD=DA，BE=EO，
∴DE∥AO，
∵EF∥BC，DE⊥EF，
∴DE⊥BC，
∴AH⊥BC，
∵AB=AC，
∴BH=HC，
∴OB=OC，OE=OF，
∴△OBC，△OEF是等腰三角形，
∵DH是Rt△ABH斜边中线，
∴DH=BD=AD，
∴△BDH，△DHA是等腰三角形，同理△HGC，△HGA都是等腰三角形．
综上所述等腰三角形有△OBC，△OEF，△HGC，△HGA，△BDH，△DHA．
22.
（1）解：∵∠BED是△ABE的外角，
∴∠BED=∠ABE+∠BAD=15°+40°=55°
（2）解：过E作BC边的垂线，F为垂足，则EF为所求的E到BC边的距离，过A作BC边的垂线AG，垂足为点G，
∴AD为△ABC的中线，BD=16，
∴BC=2BD=2×16=32，
∵△ABC的面积为80，
∴
BC AG=80，即
×32 AG=80，解得AG=5，
∵EF⊥BC于F，
∴EF∥AG，
∵E为AD的中点，
∴EF是△AGD的中位线，
∴EF=
AG=
×5=2.5.
∴E到BC边的距离为2.5
23.（1）证明：在平行四边形ABCD中，AB∥CD，AD∥BC
∴∠BAF=∠F，∠DAF=∠CEF
又∵AE平分∠BAD
∴∠BAF=∠DAF
∴∠F=∠CEF
∴CE=CF
（2）如图，连接CG、BG.
∵ABCD是平行四边形，∠ABC＝90°
∴平行四边形ABCD是矩形
∴AB=DC，AB∥DC，AD∥BC，∠BAD＝∠ADC=∠BCD＝∠ECF＝90°
∴∠F=∠BAE，∠DBC=∠ADB
∵∠BAD＝90°
，
∠BAE＝∠BAD=45°
∴AB=BE，∠F=∠BAE=45°
∴CE=CF
∴BC=BE+EC=AB+CF=CD+CF=DF
又∵G是EF的中点，∠ECF＝90°
,CE=CF
∴CG=FG=EF,∠ECG=∠ECF=45°
∴∠ECG=∠F
∴△DFG≌△BCG
∴∠FDG＝∠CBG，DG=BG
∴∠DBG=∠BDG
∵∠DBC=∠ADB,∠FDG＝∠CBG
∴∠DBC+∠CBG=∠ADB+∠FDG
即∠DBG=∠ADB+∠FDG
∴∠BDG=∠ADB+∠FDG
又∵∠BDG+（∠ADB+∠FDG）=90°
∴∠BDG=∠ADC=45°
（3）如图，连接GB、GE、GC。
∵AB//DC，∠ABC=120°
∴∠ECF=∠ABC=120°
∵FG//CE，FG=CE
∴四边形CEGF是平行四边形
由（1）得CE=CF
∴四边形CEGF是菱形，
∴EG=EC，∠GCF=∠GCE=∠ECF=60°
∴△ECG是等边三角形
∴EG=CG，∠GEC=∠EGC=60°
∴∠GEC=∠GCF
∴∠BEG=∠DCG
∵AD//BC
∴∠DAE=∠AEB
又∵∠DAE=∠BAE=∠DAB
∴∠BAE=∠AEB
∴AB=BE
在□ABCD中，AB=DC
∴BE=DC
∴△BEG
≌△DCG，
∴BG=DG，∠BGE=∠DGC
∴∠BGD=∠BGE+∠AGD=∠DGC+∠AGD=∠EGC=60°
∵BG=DG
∴∠BDG=∠DBG=（180°-∠BGD）=60°。
24.
（1）解：∵点A（-2，0），点B坐标为（4，0），
∴AB=6
∵将AD沿x轴向右平移至BC的位置，
∴AD∥BC，AD=BC
∴四边形ABCD是平行四边形
∴CD=AB=6，CD∥AB
∵OD=
AB．
∴OD=3，且CD∥AB
∴点C（6，3）
故答案为：6，（6，3）
（2）解：∵MN∥y轴，
∴点N在CD上，
∴4-t=t-3
∴t=
∴当t=
s时，MN∥y轴；②当点N在OD上时，
∵S△BCM=2S△ADN
．
∴
×3×t=2×
×2×（3-t）
解得：t=
当点N在CD上时，
∵S△BCM=2S△ADN
．
∴
×3×t=2×
×3×（t-3）
解得：t=6
综上所述：t=6或
时，S△BCM=2S△ADN
．
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)