第五章 特殊四边形单元测试卷（含解析）

中小学教育资源及组卷应用平台
浙教版2019-2020八年级数学下册第五章特殊四边形单元测试卷解析版
一、选择题（每小题3分，共30分）
1.下列命题中正确的是（
）
A. 一组对边平行的四边形是平行四边形 B. 有一个角是直角的四边形是矩形
C. 有一组邻边相等的平行四边形是菱形 D. 对角线互相垂直平分的四边形是正方形
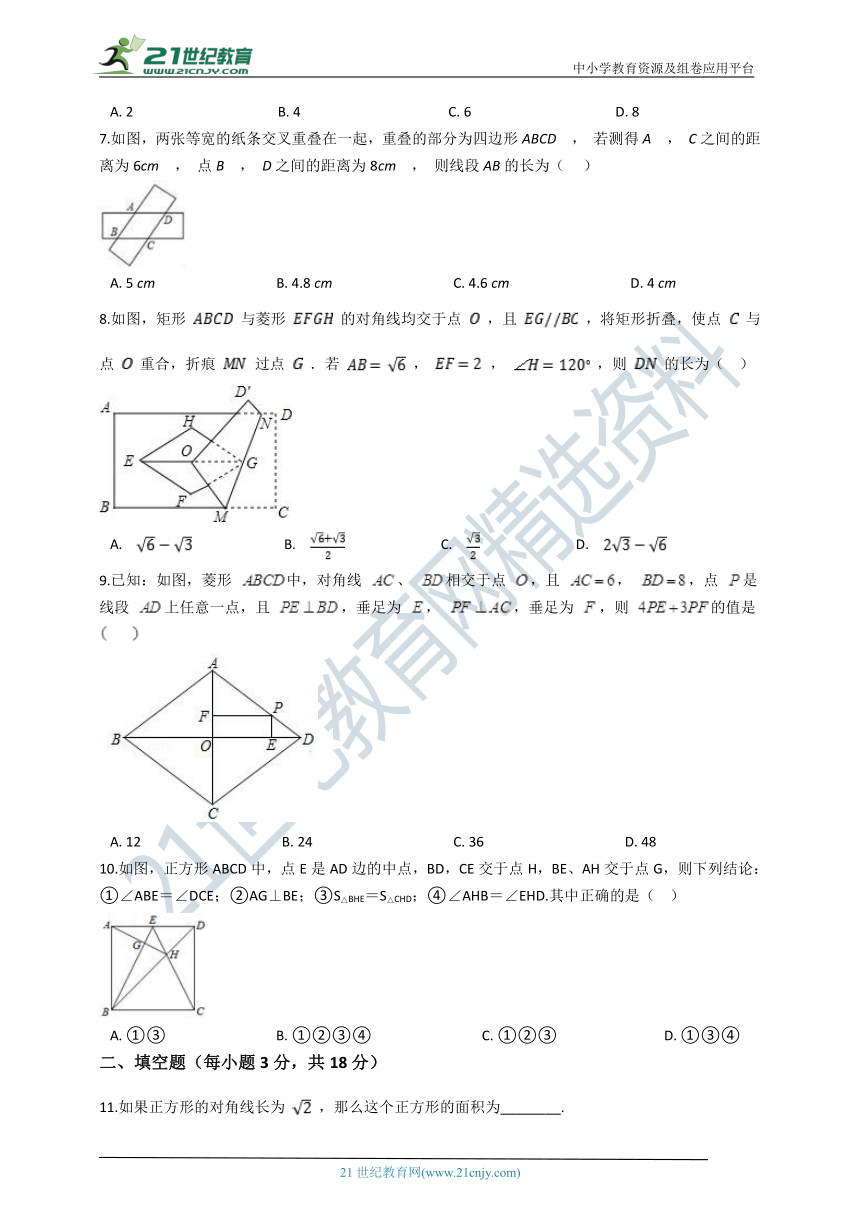
2.如图，在菱形ABCD中，E是AB的中点，F点是AC的中点，交AC于点F，如果EF＝4，那么菱形ABCD的周长为（　　）
A. 9 B. 12 C. 32 D. 24
3.如图，矩形ABCD的对角线交于点O，若∠BAO=55°，则∠AOD等于(
)
A. 105° B. 110° C. 115° D. 120°
4.如图，在正方形ABCD中，CE=MN，∠MCE=35°，那么∠ANM等于（
）
A. 45° B. 50° C. 55° D. 60°
5.如图，矩形内有两个相邻的正方形，其面积分别为2和8，则图中阴影部分的面积为（
）
A. B. 2 C. D. 6
6.如图.在矩形ABCD中，AB=6，BC=8.E是边AD的一个动点，将△BAE沿BE对折至△BFE的位置，则线段DF的最小值为（
）
A. 2 B. 4 C. 6 D. 8
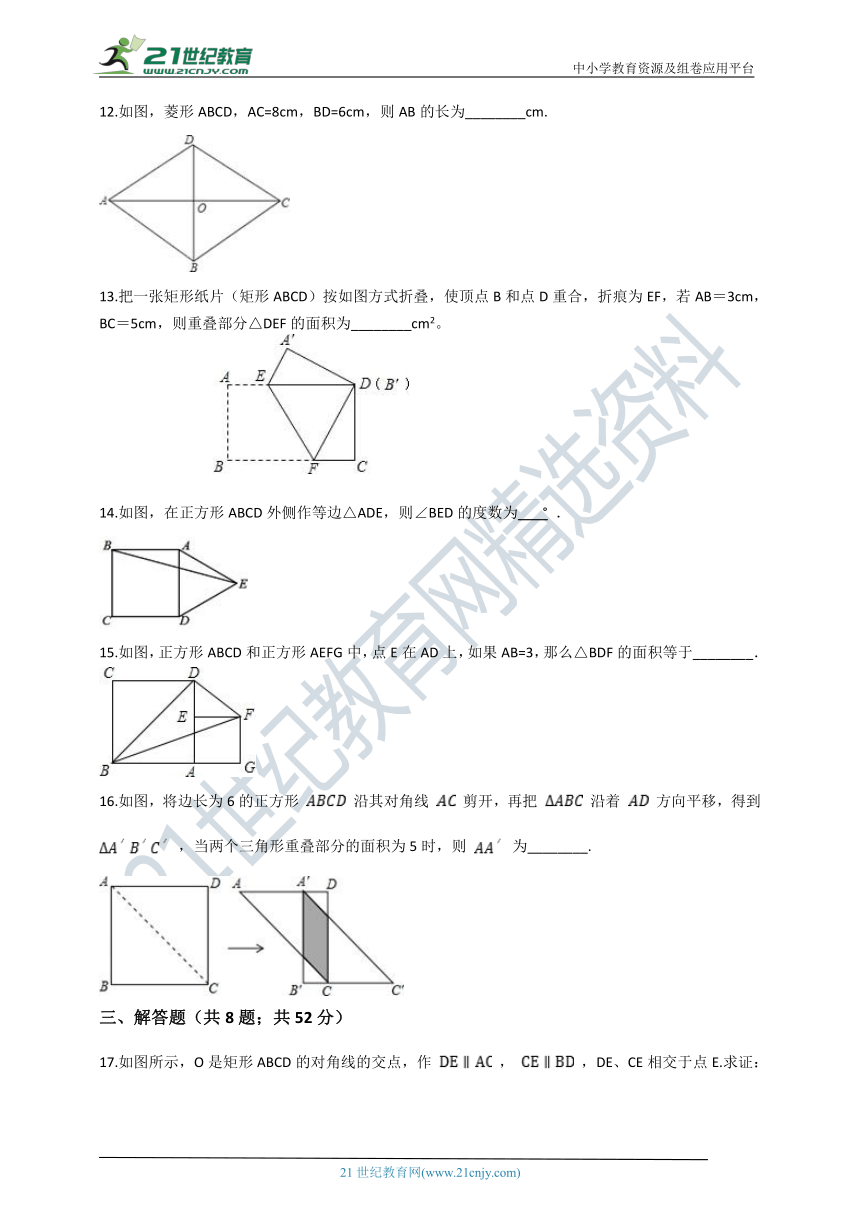
7.如图，两张等宽的纸条交叉重叠在一起，重叠的部分为四边形ABCD
，
若测得A
，
C之间的距离为6cm
，
点B
，
D之间的距离为8cm
，
则线段AB的长为（
）
A. 5
cm
B. 4.8
cm
C. 4.6
cm
D. 4
cm
8.如图，矩形
与菱形
的对角线均交于点
，且
，将矩形折叠，使点
与点
重合，折痕
过点
．若
，
，
，则
的长为（
）
A. B. C. D.
9.已知：如图，菱形
中，对角线
、
相交于点
，且
，
，点
是线段
上任意一点，且
，垂足为
，
，垂足为
，则
的值是

A. 12 B. 24 C. 36 D. 48
10.如图，正方形ABCD中，点E是AD边的中点，BD，CE交于点H，BE、AH交于点G，则下列结论：①∠ABE＝∠DCE；②AG⊥BE；③S△BHE＝S△CHD；④∠AHB＝∠EHD.其中正确的是（
）
A. ①③ B. ①②③④ C. ①②③ D. ①③④
二、填空题（每小题3分，共18分）
11.如果正方形的对角线长为
，那么这个正方形的面积为________.
12.如图，菱形ABCD，AC=8cm，BD=6cm，则AB的长为________cm.
13.把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF，若AB＝3cm，BC＝5cm，则重叠部分△DEF的面积为________cm2。
14.如图，在正方形ABCD外侧作等边△ADE，则∠BED的度数为
°
．
15.如图，正方形ABCD和正方形AEFG中，点E在AD上，如果AB=3，那么△BDF的面积等于________．
16.如图，将边长为6的正方形
沿其对角线
剪开，再把
沿着
方向平移，得到
，当两个三角形重叠部分的面积为5时，则
为________.
三、解答题（共8题；共52分）
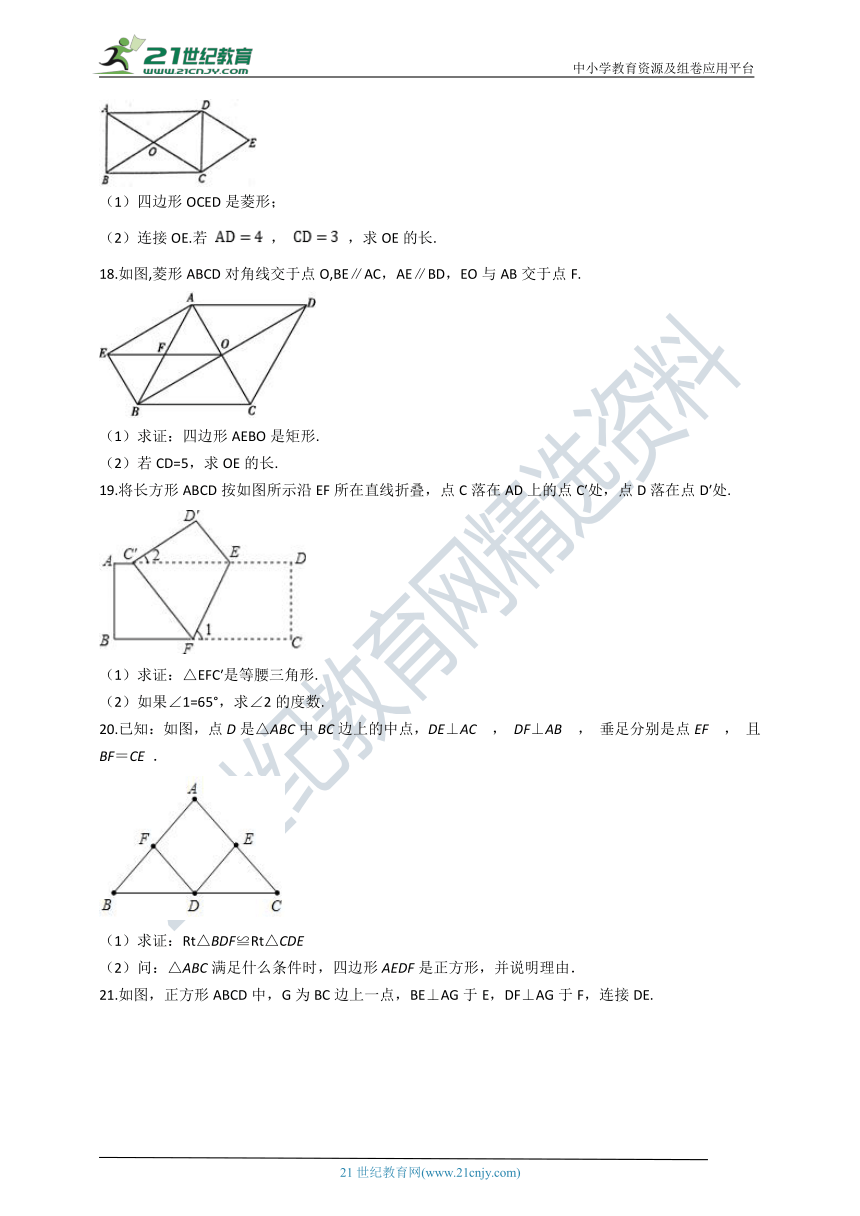
17.如图所示，O是矩形ABCD的对角线的交点，作
，
，DE、CE相交于点E.求证：
（1）四边形OCED是菱形；
（2）连接OE.若
，
，求OE的长.
18.如图,菱形ABCD对角线交于点O,BE∥AC，AE∥BD，EO与AB交于点F.
（1）求证：四边形AEBO是矩形.
（2）若CD=5，求OE的长.
19.将长方形ABCD按如图所示沿EF所在直线折叠，点C落在AD上的点C′处，点D落在点D′处.
（1）求证：△EFC′是等腰三角形.
（2）如果∠1=65°，求∠2的度数.
20.已知：如图，点D是△ABC中BC边上的中点，DE⊥AC
，
DF⊥AB
，
垂足分别是点EF
，
且BF＝CE
．
（1）求证：Rt△BDF≌Rt△CDE
（2）问：△ABC满足什么条件时，四边形AEDF是正方形，并说明理由．
21.如图，正方形ABCD中，G为BC边上一点，BE⊥AG于E，DF⊥AG于F，连接DE.
（1）求证：△ABE≌△DAF；
（2）若AF＝1，四边形ABED的面积为6，求EF的长．
22.在菱形
中，
，
是对角线
上任意一点，
是线段
延长线上一点，且
，连接
．
（1）如图1，当
是线段
的中点，且
=2时，求
的面积；
（2）如图2，当点
不是线段
的中点时，求证：
；
（3）如图3，当点
是线段
延长线上的任意一点时，（2）中的结论是否成立？若成立，请给予证明；若不成立，请说明理由．
23.如图，在四边形纸片ABCD中，∠B=∠D=90°，点E，F分别在边BC，CD上，将AB，AD分别沿AE，AF折叠，点B，D恰好都和点G重合，∠EAF=45°．
（1）求证：四边形ABCD是正方形；
（2）求证：三角形ECF的周长是四边形ABCD周长的一半；
（3）若EC=FC=1，求AB的长度．
24.已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O.
（1）如图1，连接AF、CE.求证四边形AFCE为菱形，并求AF的长；
（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止，点Q自C→D→E→C停止.在运动过程中，
①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值.
②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式.
浙教版2019-2020八年级数学下册第五章特殊四边形单元测试卷解析版
一、选择题（30分）
1.A.
应为两组对边平行的四边形是平行四边形；
B.
有一个角是直角的四边形是矩形、直角梯形、总之，只要有一个角是直角即可；
C.
符合菱形定义；
D.
应为对角线互相垂直平分且相等的四边形是正方形.
故答案为：C.
2.∵E是AB的中点，F点是AC的中点，
∴EF是△ABC的中位线，又EF=4，
∴BC=2EF=8，
∴菱形ABCD的周长为4×8=32，
故答案为：C
3.解：∵四边形ABCD是矩形，
∴OA=OB.
∴∠BAO=∠ABO=55°.
∴∠AOD=∠BAO+∠ABO=55°+55°=110°.
故答案为：B.
4.解：
过B作BF∥MN交AD于F，
则∠AFB＝∠ANM，
∵四边形ABCD是正方形，
∴∠A＝∠EBC＝90°，AB＝BC，AD∥BC，
∴FN∥BM，BF∥MN，
∴四边形BFNM是平行四边形，
∴BF＝MN，
∵CE＝MN，
∴CE＝BF，
在Rt△ABF和Rt△BCE中
∴Rt△ABF≌Rt△BCE（HL），
∴∠ABF＝∠MCE＝35°，
∴∠ANM＝∠AFB＝55°，
故答案为：C.
5.由题意可得，大正方形的边长为
，小正方形的边长为
，
∴图中阴影部分的面积为：
，
故答案为：B．
6.如图，连接DF、BD，
由图可知，DF＞BD-BF，
当点F落在BD上时，DF取得最小值，且最小值为BD-BF的长，
∵四边形ABCD是矩形，
∴AB=CD=6、BC=8，
∴BD=
，
由折叠性质知AB=BF=6，
∴线段DF长度的最小值为BD-BF=10-6=4，
故答案为：B.
7.解：作AR⊥BC于R，AS⊥CD于S，连接AC、BD交于点O．
由题意知：AD∥BC，AB∥CD，
∴四边形ABCD是平行四边形，
∵两个矩形等宽，
∴AR=AS，
∵AR BC=AS CD，
∴BC=CD，
∴平行四边形ABCD是菱形，
∴AC⊥BD，
在Rt△AOB中，∵OA=3，OB=4，
∴AB=
=5，
故答案为：A．
8.延长
交
于
点，连接
、
；如图所示：
则
，
为直角三角形，
∵四边形
是菱形，
，
∴
，
，
，
∴
，
由折叠的性质得：
，
，
，
∴
，
∵
，
∴
，
∴
，
∴
，
∴四边形
为平行四边形，
∵
，
∴四边形
为菱形，
∴
，
根据题意得：
是梯形
的中位线，
∴
，
∴
；
故答案为：A．
9.如图，连接PO，
∵四边形ABCD为菱形，
∴AC⊥BD，AO=AC=3，OD=BD=4，
S△AOD=S△APO+S△POD，
，
，
12=3PF+4PE，
即4PE+3PF=12，
故答案为：A.
10.解：∵四边形ABCD是正方形，E是AD边上的中点，
∴AE＝DE，AB＝CD，∠BAD＝∠CDA＝90°，
∴△BAE≌△CDE（SAS），
∴∠ABE＝∠DCE，
故①正确；
∵四边形ABCD是正方形，
∴AD＝DC，∠ADB＝∠CDB＝45°，DH＝DH，
∴△ADH≌△CDH（SAS），
∴∠HAD＝∠HCD，
∵∠ABE＝∠DCE
∴∠ABE＝∠HAD，
∵∠BAD＝∠BAH＋∠DAH＝90°，
∴∠ABE＋∠BAH＝90°，
∴∠AGB＝180° 90°＝90°，
∴AG⊥BE，
故②正确；
∵AD∥BC，
∴S△BDE＝S△CDE
，
∴S△BDE S△DEH＝S△CDE S△DEH
，
即：S△BHE＝S△CHD
，
故③正确；
∵△ADH≌△CDH，
∴∠AHD＝∠CHD，
∴∠AHB＝∠CHB，
∵∠BHC＝∠DHE，
∴∠AHB＝∠EHD，
故④正确；
故答案为：B.
二、填空题（18分）
11.正方形的面积=
.
故答案为：1.
12∵四边形ABCD为菱形，
∴AC⊥BD，OA=
AC=4cm，OB=
BD=3cm
在Rt△AOB中，由勾股定理得：
AB=
cm
故答案为：5.
13.解：设ED=x，则根据折叠和矩形的性质，得A′E=AE=5－x，A′D=AB=3，
根据勾股定理，得
，即
，解得
.
∴
（cm2）.
故答案为：.
14.∵正方形
，等边△
∴∠BAD=90°，∠DAE=∠ADE=60°，AB=AE
∴∠BAE=150°
∴∠BEA=15°
∴
.
15.设正方形AGEF边长为a，
∵AB=3，
∴S△BDF=S正方形ABCD+S正方形AEFG+S△DEF-S△BCD-S△BGF
=9+a2+
a（3-a）-
×3×3-
a（a+3）
=9+a2+
a-
a2-
×3×3-
a2-
a
=9-
=4.5．
故答案为：4.5．
16.解：设AA′=x，AC与A′B′相交于点E，
∵△ACD是正方形ABCD剪开得到的，
∴△ACD是等腰直角三角形，
∴∠A=45°，
∴△AA′E是等腰直角三角形，
∴A′E=AA′=x，
A′D=AD-AA′=6-x，
∵两个三角形重叠部分的面积为5，
∴x（6-x）=5，
整理得，x2-6x+5=0，
解得x1=1，x2=5，
即移动的距离AA′等于1或5.
故答案是：1或5.
三、解答题（52分）
17.
（1）证明：∵
，
，
∴四边形OCED是平行四边形.
∴
，
∵四边形ABCD是矩形，
∴
.
∴
.
∴四边形OCED是菱形；
（2）解：如图，连接OE.
∵四边形OCED是菱形；
∴
，
又∵
，
∴
.
∵
，
，
∴四边形AOED是平行四边形，
∴
.
18.
（1）证明:∵BE
AC，AE
BD,
∴四边形AEBO是平行四边形.
又∵菱形ABCD对角线交于点O,
∴AC⊥BD,即∠AOB=90°,
∴四边形AEBO是矩形.
（2）解：∵四边形AEBO是矩形,
∴EO=AB,
在菱形ABCD中,AB=DC.
∴EO=DC=5
19.
（1）证明：四边形EFC′D′是将长方形ABCD中的四边形CDEF沿EF所在直线折叠得到的，
∴∠EFC′=∠1，
∵AD∥BC，
∴∠1=∠FBC′，
∴∠EFC′=′FEC′，
∴FC′=EC′，
∴△EFC′是等腰三角形
（2）解：∵∠1=∠FEC′=∠EFC′，∠1=65°，
∴∠EC′F=180°﹣∠FEC′﹣∠EFC′=180°﹣65°=65°=50°，
∵∠D′C′F=∠2+∠EC′F=∠C=90°，
∴∠2=90°﹣∠EC′F=40°，
∴∠2=40°.
20.
（1）解：∵DE⊥AC，DF⊥AB，
∴∠BDF=∠CED=90°
∵点D是△ABC中BC边上的中点，
∴BD=CD，在
中，
，
（2）解：当△ABC满足∠A=90°（答案不唯一）时，四边形AEDF是正方形；理由如下：
∵∠BDF=∠CED=90°，∠A=90°，
∴四边形AEDF是矩形，
∴DE=DF，
∴四边形AEDF是正方形．
21.
（1）证明：在正方形ABCD中
AD=AB
∠BAD=90°
∴∠DAF+∠BAE=90°
又∵BE⊥AG，DF⊥AG
∴∠AFD=∠BEA=90°
∴∠DAF+∠ADF=90°
∴∠BAE=∠ADF
∴△ABE≌△DAF（AAS）
（2）∵△ABE≌△DAF
∴BE=AF=1，DF=AE=AF+EF=1+EF
∵
S四边形ABED的面积=S△ABE+S△ADE=6
∴
即
解得
EF=2（EF=-5舍去）
22.
（1）解：
∵四边形ABCD是菱形，
∴AB=AC，
∵∠ABC=60°，
∴△ABC是等边三角形，
∴AC=AB=2,
∴S△ABC=AC×BE=×2×=.
（2）证明：如图，连接ED、FD，
∵四边形ABCD是菱形，∠ABC=60°
∴AB=CD=AD，∠BAE=∠EAD=∠DCF=60°，AE=CF，
∴△ABE≌△ADE≌△DCF，
∴BE=ED=DF,
∠ADE=∠CDF，
∴∠EDF=∠EDC+∠CDF=∠CDE+∠EDA=60°，
∴△EDF为等边三角形，
∴EF=FD=ED，
∴BE=EF；
（3）证明：如图，连接DE、DF，
∵四边形ABCD是菱形，∠ABC=60°
∴AB=CD=AD，∠BAE=∠EAD=∠DCF=60°，AE=CF，
∴△ABE≌△ADE≌△DCF，
∴BE=ED=DF,
∠ADE=∠CDF，
∴∠ACD+∠CDE=∠FDE+∠EDC，
∴∠EDF=∠ADC=60°，
∴△EDF为等边三角形，
∴EF=DE=BE，
∴BE=EF.
23.
（1）证明：由题意得，∠BAE=∠EAG，∠DAF=∠FAG，
∴∠BAD=2∠EAF=90°，
∴四边形ABCD是矩形，
∵AB=AG，AD=AG，
∴AB=AD，
∴四边形ABCD是正方形
（2）证明：∵EG=BE，FG=DF，
∴EF=BE+DF，
∴△ECF的周长=EF+CE+CF=BE+DF+CE+CF=BC+CD，
∴三角形ECF的周长是四边形ABCD周长的一半
（3）解：∵EC=FC=1，
∴BE=DF，
∴EF=
，
∵EF=BE+DF，
∴BE=DF=
EF=
，
∴AB=BC=BE+EC=
+1．
24.
（1）证明：①∵四边形ABCD是矩形，
∴AD∥BC，
∴∠CAD=∠ACB，∠AEF=∠CFE，
∵EF垂直平分AC，垂足为O，
∴OA=OC，
∴△AOE≌△COF，
∴OE=OF，
∴四边形AFCE为平行四边形，
又∵EF⊥AC，
∴四边形AFCE为菱形，
②设菱形的边长AF=CF=xcm，则BF=（8﹣x）cm，
在Rt△ABF中，AB=4cm，
由勾股定理得42+（8﹣x）2=x2
，
解得x=5，
∴AF=5cm.
（2）解：①显然当P点在AF上时，Q点在CD上，此时A、C、P、Q四点不可能构成平行四边形；
同理P点在AB上时，Q点在DE或CE上，也不能构成平行四边形.
因此只有当P点在BF上、Q点在ED上时，才能构成平行四边形，
∴以A、C、P、Q四点为顶点的四边形是平行四边形时，PC=QA，
∵点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，
∴PC=5t，QA=12﹣4t，
∴5t=12﹣4t，
解得
，
∴以A、C、P、Q四点为顶点的四边形是平行四边形时，
秒.
②由题意得，以A、C、P、Q四点为顶点的四边形是平行四边形时，点P、Q在互相平行的对应边上.
分三种情况：
i）如图1，当P点在AF上、Q点在CE上时，AP=CQ，即a=12﹣b，得a+b=12；
ii）如图2，当P点在BF上、Q点在DE上时，AQ=CP，即12﹣b=a，得a+b=12；
iii）如图3，当P点在AB上、Q点在CD上时，AP=CQ，即12﹣a=b，得a+b=12.
综上所述，a与b满足的数量关系式是a+b=12（ab≠0）.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)