4.4~4.6 平行四边形同步测试题(含答案)
文档属性
| 名称 | 4.4~4.6 平行四边形同步测试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-28 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教数学八下单元检测
平行四边形4.4~4.6
选择题(每小题3分,共30分)
1.如图,在△ABC中,D、E分别是AB、AC边上的中点,若BC=6,则DE等于( )
A.5 B.4 C.3 D.2
2. 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD?? B.AB=CD,AO=CO
C.AD∥BC,AD=BC? D.AD∥BC,AB∥CD
3.如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是( )
A.DC>EF B.DC<EF C.DC=EF D.无法比较
4.下列说法正确的是( )
A.每个命题都有逆命题 B.每个定理都有逆定理
C.只有真命题才有逆命题 D.命题与逆命题同真假
5.如图,在平行四边形ABCD中,AC与BD交于点O,E是BC边的中点,AB=4,则OE的长为( )
A.1 B.2 C.3 D.5
6.如果等边三角形的边长为3,那么连结各边中点所成的三角形的周长为( )
A.9 B.6 C.3 D.
7. 点P(a, 1)与Q(-2, b)关于坐标原点对称,则a, b的值分别是( )
A.2,-1 B.-2,1 C.2,1 D.
8.已知平面直角坐标系内,O(0,0), A(2,6), C(6,0)若以O,A,C,B为顶点的四边形是平行四边形,则点B不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.如图,设P为平行四边形ABCD内的一点,△PAB、△PBC、△PDC、△PDA的面积分别记为S1、S2、S3、S4,则有( )
A.S1=S4 B.S1+S2=S3+S4 C.S1+S3=S2+S4 D.以上都不对
10.如图,将一个边长分别为4、8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )
A. B. C. D.
填空题(每小题3分,共24分)
11. 点A(5,-1)关于直角坐标原点对称的点的坐标是( ).
12. 定理“对角线互相平分的四边形是平行四边形”的逆定理是 .
13. 如图,A、B两地间有一池塘阻隔,为测量A、B两地的距离,在地面上选一点C,连接CA、CB的中点D、E.若DE的长度为30m,则A、B两地的距离为 m.
14. 平行四边形两邻角的平分线相交所成的角的大小为 .
15. 依次连接四边形各边中点所形成的四边形一定是 .
16.如图所示,EF是△ABC的中位线,BD平分∠ABC,交EF于D,若EF=3,DF=1,则EB= .
17.如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,
AH⊥BC于H,FD=8 , 则HE= .
如图,ABCD中,用直尺和圆规作∠BAD的平分线
AG交BC于点E,若BF=6,AB=5,则AE的长为 .
解答题(共46分)
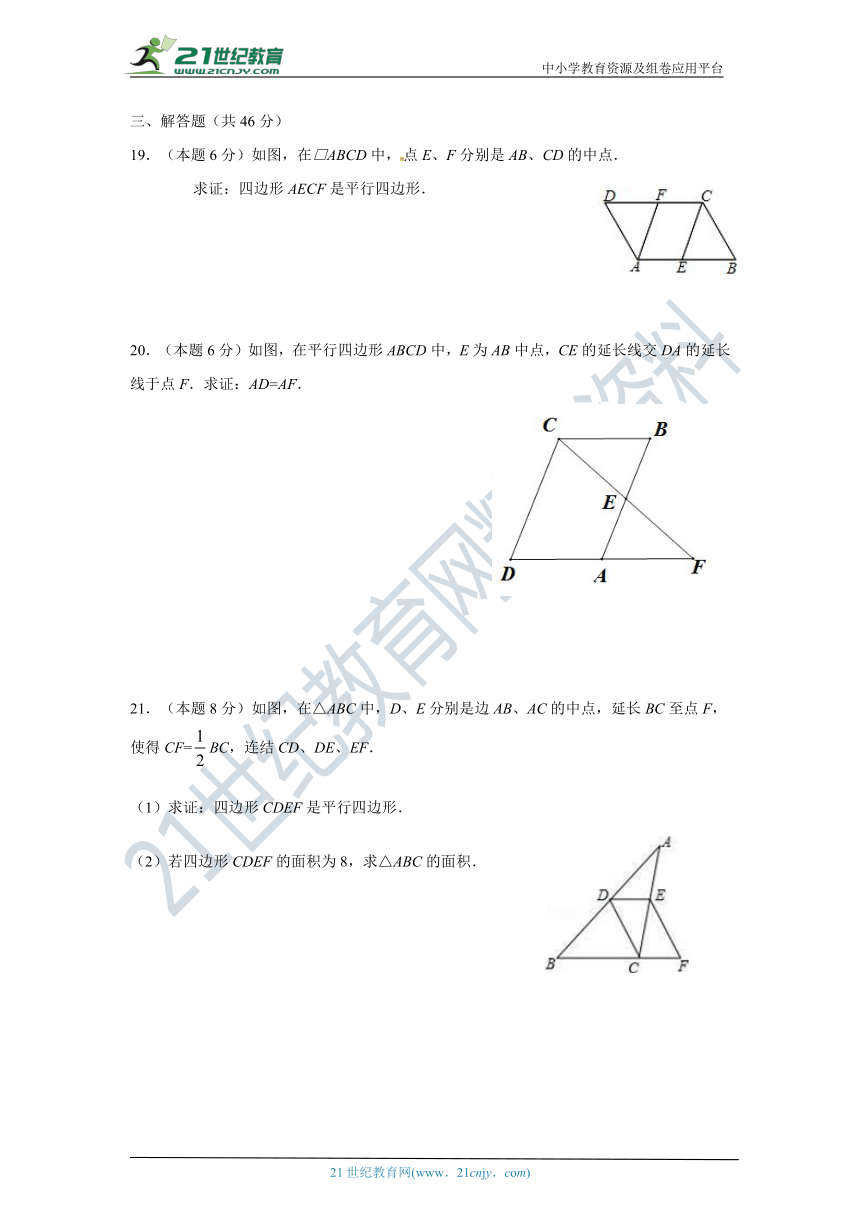
19.(本题6分)如图,在□ABCD中,点E、F分别是AB、CD的中点.
求证:四边形AECF是平行四边形.
20.(本题6分)如图,在平行四边形ABCD中,E为AB中点,CE的延长线交DA的延长线于点F.求证:AD=AF.
21.(本题8分)如图,在△ABC中,D、E分别是边AB、AC的中点,延长BC至点F,使得CF=BC,连结CD、DE、EF.
(1)求证:四边形CDEF是平行四边形.
(2)若四边形CDEF的面积为8,求△ABC的面积.
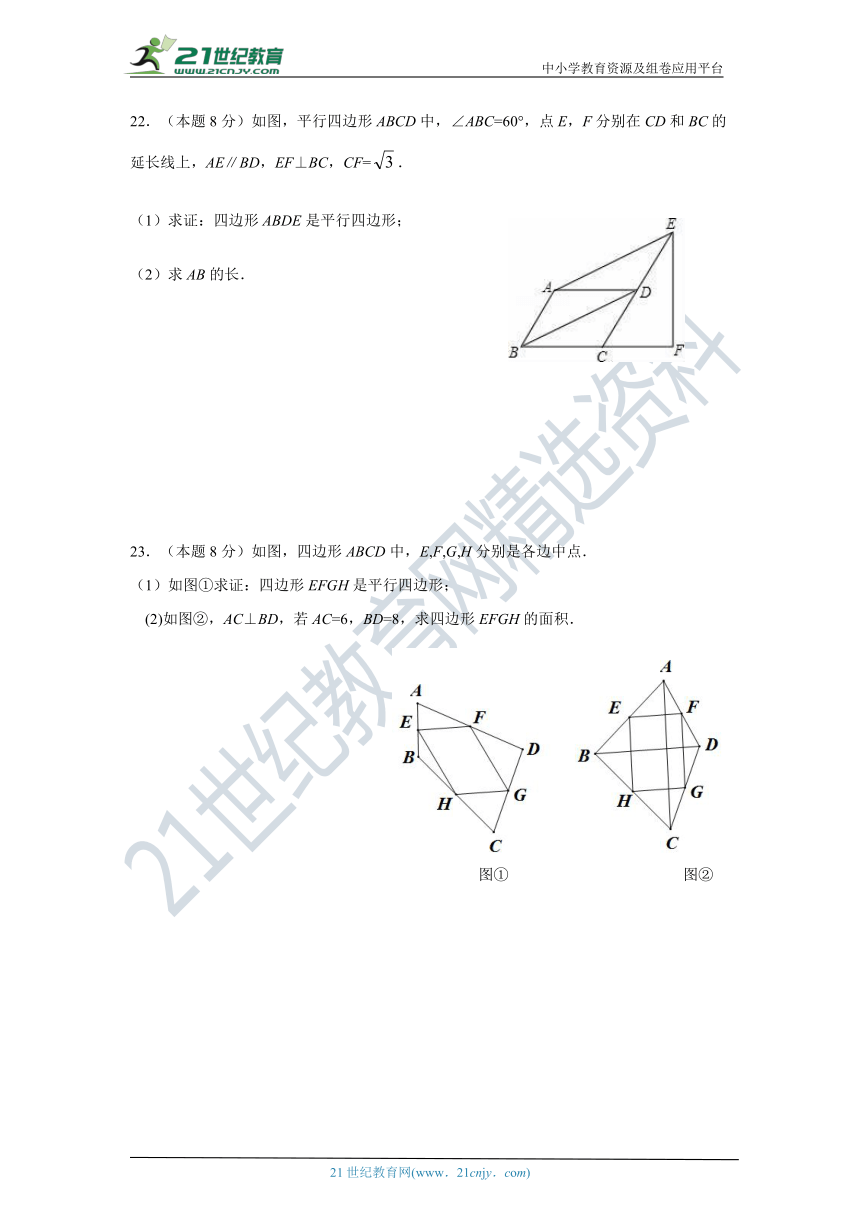
22.(本题8分)如图,平行四边形ABCD中,∠ABC=60°,点E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=.
(1)求证:四边形ABDE是平行四边形;
(2)求AB的长.
23.(本题8分)如图,四边形ABCD中,E,F,G,H分别是各边中点.
(1)如图①求证:四边形EFGH是平行四边形;
(2)如图②,AC⊥BD,若AC=6,BD=8,求四边形EFGH的面积.
24.(本题10分)如图,四边形ABCD,CD∥AB,AD=BC,对角线AC、BD交于点O,∠ACD=60°,点P、Q、S分别为OA、BC、OD的中点,求证:△SPQ是等边三角形.
(?http:?/??/?www.czsx.com.cn?/??)
附加题25. 如图,在平行四边形ABCD中,AD=4 cm,∠A=60°,BD⊥AD. 一动点P从A出发,以每秒1 cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD .
(1) 当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2) 当点P运动2秒时,另一动点Q也从A出发沿A→B→C的路线运动,且在AB上以每秒1 cm的速度匀速运动,在BC上以每秒2 cm的速度匀速运动. 过Q作直线QN,使QN∥PM. 设点Q运动的时间为t秒(0≤t≤10),直线PM与QN截平行四边形ABCD所得图形的面积为S cm2 .
① 求S关于t的函数关系式;② 求S的最大值.
答案
一、选择题:CBCAB DACCD
二、填空题:
11.(-5,1)
12.平行四边形的对角线互相平分
13.15
14.90
15.平行四边形
16.2
17.8
18.8
解答题
19.证明CF=AE,又CF∥AE,∴四边形AECF是平行四边形
20. 可连结AC,证四边形ACBF是平行四边形,得AF=BC,又AD=BC,∴AD=AF
21. ∵在△ABC中,D、E分别是边AB、AC的中点,∴DE∥BC且DE=BC.
又∵CF=BC,∴DE=CF,∴四边形CDEF是平行四边形.
(2∵DE∥BC,∴四边形CDEF与△ABC的高相等,设为h,又∵CF=BC,
∴S△ABC=BC?h=CF?h=8,
22. ∵四边形ABCD是平行四边形,∴AB∥DC,AB=CD,∵AE∥BD,
∴四边形ABDE是平行四边形;(2)由(1)知,AB=DE=CD,即D为CE中点,
∵EF⊥BC,∴∠EFC=90°,∵AB∥CD,∴∠DCF=∠ABC=60°,∴∠CEF=30°,
∴AB=CD=.
23. (1)连接AC,利用中位线定理得:EH=AC,EH∥AC,FG=AC,FG∥AC,∴EH∥FG
且EH=FG,∴四边形EFGH是平行四边形
(2)可得四边形ABCD的面积是24,而四边形EFGH的面积是四边形ABCD的面积的一半,可得四边形EFGH的面积是12
24. 连CS,PB,CD‖AB,AD=BC,∠ACD=60°,△OCD为等边三角形,又S为OD中点
∴CS垂直于SB,Rt△CSB中,Q为斜边中点 ∴ SQ=BQ=CQ=CB
同理PQ=BQ=CQ=CB P,S分别为OA,OD的中点,所以SP=AD
又AD=BC ∴ SQ=SP=PQ ∴ △SPQ是等边三角形
25.(1) AP=2 cm,由∠A=60°,知AE=1,PE=∴ SΔAPE=
(2) ① 当0≤t≤6时,点P与点Q都在AB上运动,
设PM与AD交于点G,QN与AD交于点F,
则AQ=t,AF=,QF=,AP=t+2,AG=1+,PG=.
∴ 此时两平行线截平行四边形ABCD是一个直角梯形,[来&源:中^国%教育出*版网#]
其面积为(PG + QF)×AG÷2 S=.
当6≤t≤8时,点P在BC上运动,点Q仍在AB上运动.
设PM与DC交于点G,QN与AD交于点F,
则AQ=t,AF=,DF=4-,
QF=,AP=t+2,BP=t-6,[来&#源:%中国^教育~出版网]
CP=AC- AP=12-(t+2)=10-t,
PG=,而BD=,
故此时两平行线截平行四边形ABCD的面积为平行四边形的面积减去两个三角形面积 S=.
当8≤t≤10时,点P和点Q都在BC上运动.
设PM与DC交于点G,QN与DC交于点F,
则AQ=2t-8,CQ= AC- AQ= 12-(2t-8)=20-2t, ~p.c@om]
QF=(20-2t),CP=10-t,PG=.
∴ 此时两平行线截平行四边形ABCD的面积为.
②(附加题)当0≤t≤6时,S的最大值为;
当6≤t≤8时,S的最大值为;
当8≤t≤10时,S的最大值为;[来源:@中%#&教网^]
所以当t=8时,S有最大值为 .
第1题图 第2题图 第3题图 第4题图
第9题图 第10题图 第13题图 第14题图
第17题图
第18题图
图① 图②
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
