第四章 平行四边形单元检测试题（含答案）

中小学教育资源及组卷应用平台


浙教数学八下单元检测
平行四边形综合
一、选择题（每小题3分，共30分）
1． 平行四边形的一个内角为40°，它的对角等于（　　）
A．?40°????????????????? B．?140°????????????????????? C．?150°?????????? D．?50°
2．平行四边形不一定具有的特征是 ( )
A． 两组对边分别平行 B． 两组对角分别相等 C．对角线相等 D．内角和为
3．下列多边形中，内角和与外角和相等的是（ ）
A．四边形 B．五边形 C．六边形 D．八边形
4． 如图，在△ABC中，点D、E、F分别是AB、AC、BC的中点，若△ABC的周长为12，则△DEF的周长为（ ）
A．12 B．16 C．20 D．24




5． 如图，在?ABCD中，BM是∠ABC的平分线交CD于点M，且MC=2，则AD等于（　　）
A．1?? ? B．2??? C．3??? D．4
6． 如图，在平行四边形ABCD中，AC、BD相交于点O，则下列结论不一定成立的是（　　）
A．BO=DO?? ? B．S△COD=S△AOD? C．∠BAD=∠BCD?????? D．AC=BD
7．平行四边形的一边为10cm,则两条对角线的长可以是 ( )
A． 12和8 B．26和4 C．24和4 D．24和12
8． 如图，一块平行四边形的土地被分成4块，其中过点O的两小路分别与邻边平行．其中种植不同的花卉的三块的面积分别为20m2、30m2、36m2，则第四块的面积为（???）
A．46m2?????????????? B．50m2????????????????????? C．54m2????????????????????? D．60m2
9． 某广场上一个形状是平行四边形的花坛（如图），分别种有红、黄、蓝、绿、橙、紫6种颜色的花．如果有，，那么下列说法中错误的是（ ）
A．红花、绿花种植面积一定相等
B．紫花、橙花种植面积一定相等
C．红花、蓝花种植面积一定相等
D．蓝花、黄花种植面积一定相等
如图，已知O是四边形ABCD内一点，OA=OB=OC，
∠ABC=∠ADC=70°，则∠DAO+∠DCO的大小是(　　)
A．70°　　　　B．110°　　　C．140°　　　　D．150?

二、填空题（每小题3分，共24分）
11． 在四边形ABCD中，若∠A＝∠C＝90°，∠B＝60°,则∠D＝______°．
12．在平面直角坐标系中，点关于原点对称点的坐标是 ．
13．如图，在□ABCD中，DB=CD，∠C=70°，AE⊥BD于点E．则∠DAE= °．






14．如图，BC为固定的木条，AB，AC为可伸缩的橡皮筋．当点A在与BC平行的轨道上滑动时，△ABC的面积将如何变化 ．(变大、变小、不变、不一定)
15如图，在□ABCD中，Ｅ是BC上一点，且AB=BE， AE 的延长线交DC的延长线于点F，若∠F=50°，则∠D= °．
16．如图，□ABCD中，AB=4，BC=6，BC边上的高AE=2，则DC边上的高AF的长为_　_．
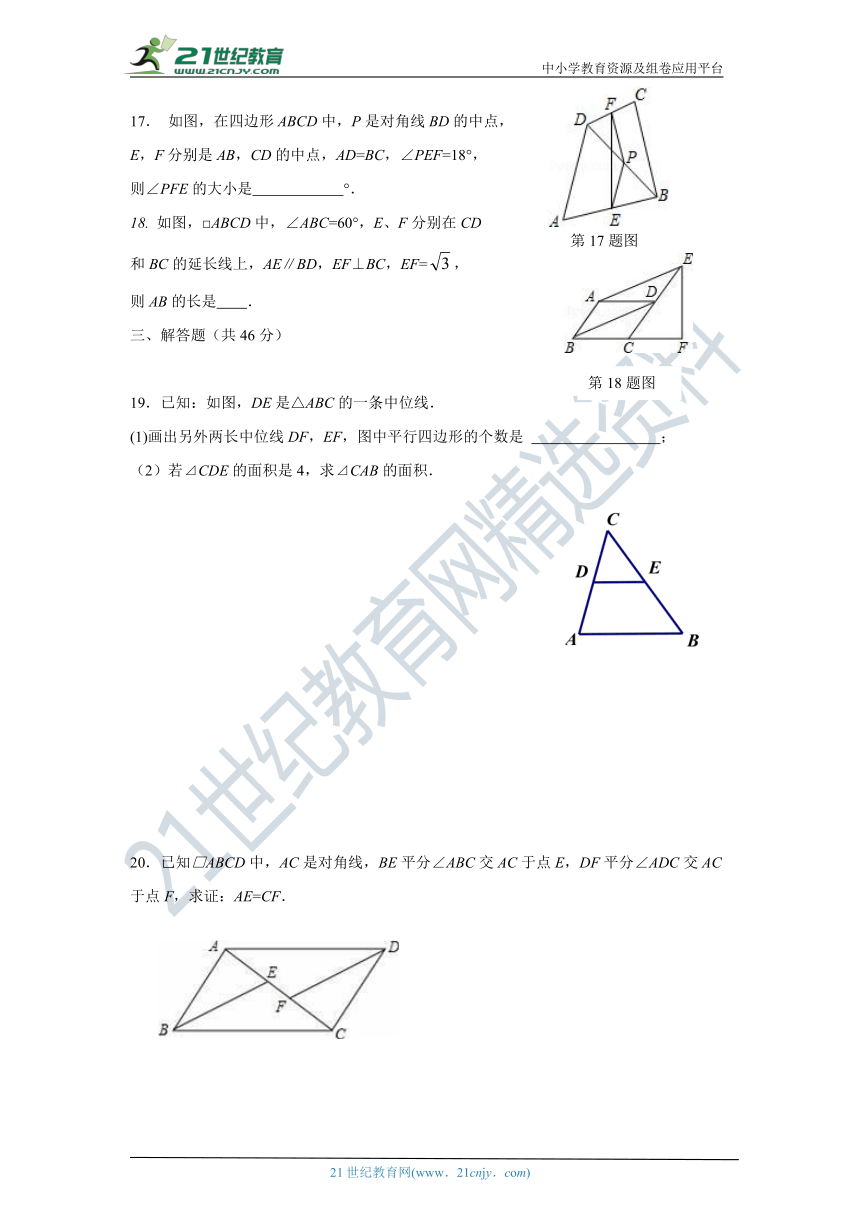
17． 如图，在四边形ABCD中，P是对角线BD的中点，
E，F分别是AB，CD的中点，AD=BC，∠PEF=18°，
则∠PFE的大小是　　　　　　°．
如图，□ABCD中，∠ABC=60°，E、F分别在CD
和BC的延长线上，AE∥BD，EF⊥BC，EF=，
则AB的长是　　．
三、解答题（共46分）

19．已知：如图，DE是△ABC的一条中位线．
(1)画出另外两长中位线DF，EF，图中平行四边形的个数是 ；
（2）若⊿CDE的面积是4，求⊿CAB的面积．










20．已知□ABCD中，AC是对角线，BE平分∠ABC交AC于点E，DF平分∠ADC交AC于点F，求证：AE=CF．


21． 在四边形ABCD中，∠A=135°，∠B=∠D=90°，BC=，AD=2，
求四边形ABCD的面积．







22．已知：如图，在△ABC中，中线BE，CD交于点O，F，G分别是OB，OC的中点．求证：四边形DFGE是平行四边形．


23．（本题8分） 如图，已知ABCD中, ，点B在轴正半轴上且，．
(1)用含的代数式表示点的坐标；
(2)若有一条直线能把ABCD的面积分成相等的两部分,求的值．







24． （本题10分）如图，四边形ABCD中，BD垂直平分AC，垂足为点F，E为四边形ABCD外一点，且∠ADE=∠BAD，AE⊥AC．
（1）求证：四边形ABDE是平行四边形；
（2）如果DA平分∠BDE，AB=5，AD=6，求AC的长．




附加题：
25．在△ABC中，AB=AC，点D在边BC所在的直线上，过点D作DF∥AC交直线AB于点F，DE∥AB交直线AC于点E．
（1）当点D在边BC上时，如图①，求证：DE+DF=AC；
（2）当点D在边BC的延长线上时，如图②；当点D在边BC的反向延长线上时，如图③，请分别写出图②、图③中DE，DF，AC之间的数量关系，不需要证明；
（3）若AC=6，DE=4，则DF=　　　　　　．

答案
一、选择题
ACCDB DDCCD
二、填空题:
11．120°
12．
13．20°
14．不变
15．65°
16．3
17．18°
18．1
三、解答题
19．（1） 画图略，3；（2）⊿CAB的面积是⊿CDE的面积的4倍，即面积为12
20． ∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∠ABC=∠CDA，∵BE平分∠ABC，DF平分∠ADC，∴∠ABE=∠CDF，∵AB∥CD，∴∠BAE=∠DCF∴△ABE≌△CDF（ASA）．∴AE=CF．
21． 发别延长CD，BA交于点E．∵∠DAB=135°，∴∠EAD=∠C=∠E=45°，∴BE=BC=，AD=ED=2，∴四边形ABCD的面积=
22． 在△ABC中，∵BE、CD为中线∴AD=BD，AE=CE，∴DE∥BC且DE=BC．
在△OBC中，∵OF=FB，OG=GC，∴FG∥BC且FG=BC．∴DE∥FG，DE=FG．∴四边形DFGE为平行四边形．

23． 点C在点B的正右方1个单位，∴；
对称中心的坐标是，直线经过，得
24．（1）∵AE⊥AC，BD垂直平分AC，∴AE∥BD，∵∠ADE=∠BAD，∴DE∥AB，∴四边形ABDE是平行四边形；
（2）解：∵DA平分∠BDE，∴∠BAD=∠ADB，∴AB=BD=5，设BF=x，则52﹣x2=62﹣（5﹣x）2，解得，，∴AF＝，∴AC=2AF=．
25． （1）∵DF∥AC，DE∥AB，
∴四边形AFDE是平行四边形．∴AF=DE，∵DF∥AC，∴∠FDB=∠C
又∵AB=AC，∴∠B=∠C，∴∠FDB=∠B∴DF=BF∴DE+DF=AB=AC；
?（2）图②中：AC+DE=DF．图③中：AC+DF=DE．
?（3）当如图①的情况，DF=AC﹣DE=6﹣4=2；当如图②的情况，DF=AC+DE=6+4=10．
答案是：2或10．






第4题图

第8题图

第5题图

第6题图

黄

蓝

紫

橙

红

绿

A

G

E

D

H

C

F

B

第9题图

第10题图

第13题图 第14题图 第15题图 第16题图




第17题图

第18题图






21世纪教育网 www．21cnjy．com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www．21cnjy．com)