5.3~5.4 特殊平行四边形及综合(含答案)
文档属性
| 名称 | 5.3~5.4 特殊平行四边形及综合(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-29 10:41:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版八下数学单元检测
特殊四边形5.3~5.4
一、选择题(每小题3分,共30分)
1.矩形ABCD的对角线AC的长为5,则对角线BD的长为( ??)
?? ????A.5 ?????? B. C. D.
2.□ABCD中,AC,BD是两条对角线,如果添加一个条件,即可识别□ABCD是矩形,那么这个条件是(?????)?????????
A.AB=BC??? ?????????? B.AC=BD????????????????? C.AC⊥BD??????? ???? D.AB⊥BD
3.如图,矩形两条对角线所成的钝角为120°,若一条对角线AD的长是2,则AC的长为(???)
A. 1 B.2 C.3 D.
4.如图,菱形ABCD 中,对角线AC、BD交于点O,菱形ABCD周长为32,点P是边CD的中点,则线段OP的长为(???)
A.3???? B.5 ???? ??C.8??? D.4
5.以不在同一直线上的三个点为顶点作平行四边形,最多能作的个数是(????)
A.1??? B.2????? C.3? ? D.4
6.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长( )
A.4????? B.6????? ?? C.8??????? D.10
7.下列性质中,菱形具有但平行四边形不一定具有的是( )
A.对边相等? B.对角线相等 C.对角线互相垂直? D.对角线互相平行
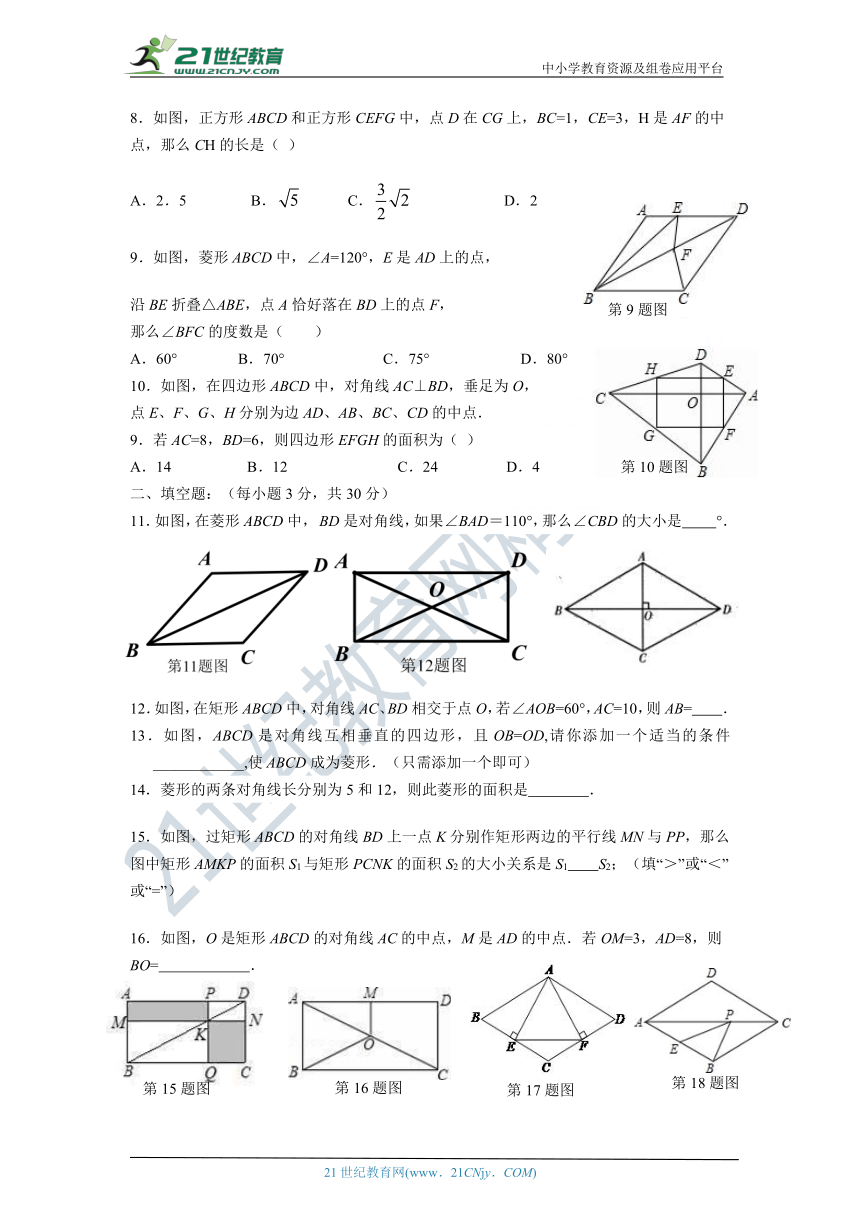
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是(??)
A.2.5 ?????? ?B.???? ????C.???? ????D.2
9.如图,菱形ABCD中,∠A=120°,E是AD上的点,
沿BE折叠△ABE,点A恰好落在BD上的点F,
那么∠BFC的度数是( )
A.60° B.70° C.75° D.80°
10.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,
点E、F、G、H分别为边AD、AB、BC、CD的中点.
若AC=8,BD=6,则四边形EFGH的面积为(??)
A.14????? ?B.12???? ???C.24?????? D.4
二、填空题:(每小题3分,共30分)
11.如图,在菱形ABCD中, BD是对角线,如果∠BAD=110°,那么∠CBD的大小是?????????°.
12.如图,在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= .
13.如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 ____________,使ABCD成为菱形.(只需添加一个即可)
14.菱形的两条对角线长分别为5和12,则此菱形的面积是 .
15.如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PP,那么图中矩形AMKP的面积S1与矩形PCNK的面积S2的大小关系是S1 S2;(填“>”或“<”或“=”)
16.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若OM=3,AD=8,则BO= .
17.如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是_________________.
18.如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是??? ???.
三、解答 题(共46分)
19.(本题6分)如图,点E、F、G、H分别为矩形ABCD四条边的中点,证明:四边形EFGH是菱形.
20. (本题6分) 如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
(1)请你判断所画四边形的性状,并说明理由;
(2)连接EF,若AE=8CM,∠A=60°,求线段EF的长.
21. (本题8分)如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3CM,BC=5CM,∠B=60°,当AE= CM时,四边形CEDF是菱形.
22.(本题8分) 如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
23.(本题8分)如图,在菱形ABCD中,AC,BD相交于点O,已知E为AB的中点且?DE┴AB.
(1)求∠ABC的度数;
(2)若AC=,求DE的长.
24.(本题10分)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
附加题
25. 如图,在Rt△ABC中,∠B=90°,AC=60 ,∠A=60°,点D从点C出发沿CA方向以4 CM/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 单位/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
???????
????????????????????????????????????????????????????
答案
一、选择题:CBADC CCBCB
二、填空题:
11.35
12.5
13.如AO=CO
14.30
15.=
16.5
17.
18.
三、解答题
19. 可证⊿AEH与⊿BEF全等,同理可得四个三角形均全等,可得EH=EF=GH=GF,得四边形EFGH是菱形.
20. (1)菱形,理由是四条边都相等;(2)⊿AEF是等边三角形,EF=AE=8
21.四边形ABCD是平行四边形,∴CF∥ED,∴∠FCD=∠GCD,∵G是CD的中点,
∴CG=DG,,∴△CFG≌△EDG(ASA),∴FG=EG,∴四边形CEDF是平行四边形;
?(2)∵四边形ABCD是平行四边形,∴AD=BC=5,CD=AB=3,∠ADC=∠B=60°,∵当DE=CE时,四边形CEDF是菱形,∴当△CED是等边三角形时,四边形CEDF是菱形,
∴DE=CD=3,∴AE=AD﹣DE=2,
22. ∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴AF∥EC,
∵BE=DF,∴AF=EC,∴四边形AECF是平行四边形;
(2)∵四边形AECF是菱形,∴AE=CE,∴∠1=∠2,∵∠BAC=90°,
∴∠3=∠90°-∠2,∠4=∠90°-∠1,∴∠3=∠4,∴AE=BE,∴BE=AE=CE=?BC=5。
23. ∵四边形ABCD是菱形,?AB=AD,AD║BC???∴∠DAB+∠ABC=180°.
?????∵E为AB的中点,DE┴AB,?∴AD=BD.???∴AD=BD=AB.
?????∴?△ABD为等边三角形.∴∠DAB=60?°.∴∠ABC=120°?.
(2)∵四边形ABCD是菱形,?∴BD┴AC于O,AO=AC=
?????∵DE┴AB于E,∴∠AOB=∠DEB=90°.
?????∵DB=AB,∠ABO=∠DBE????????
?????∴⊿ABO≌⊿DBE.??∴DE=AO=
24. (1)OE=OF.可证得∴OE=CO,OC=OF.
∴OE=OF.
(2)四边形BCFE不可能是菱形,若四边形BCFE为菱形,则BF⊥EC,
而由(1)可知FC⊥EC,在平面内过同一点F不可能有两条直线同垂直于一条直线.当
(3)点O运动到AC中点时,且△ABC是直角三角形(∠ACB=90°)时,四边形AECF是正方形.
点O运动到AC中点时,AECF为矩形,
又∵AC⊥EF.
∴?AECF是正方形.
∴当点O为AC中点且△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.
25. 在△DFC中,∠DFC=90°,∠C=30°,DC=4t,∴DF=2t.?∵AE=2t,∴AE=DF.????????????????????
(2)能.理由如下:
∵AB⊥BC,DF⊥BC,∴AE∥DF.
∵AE=DF,
∴四边形AEFD为平行四边形,AE=AD=AC-DC=60-4t=2t.解得t=10,
∴当t=10秒时,四边形AEFD为菱形.???????
(3)①当∠DEF=90°时,由(2)知EF∥AD,??∴∠ADE=∠DEF=90°.
???∵∠A=60°,∴AD=AE=t.又AD=60-4t,即60-4t=t.?
?解得t=12.?????????????????????????????????
②当∠EDF=90°时,四边形EBFD为矩形,在Rt△AED中,∠A=60°,则∠ADE=30°,
∴AD=2AE,即60-4t=4t,解得t=.???????????
③若∠EFD=90°,则E与B重合,D与A重合,此种情况不存在.
∴当t=秒或12秒时,△DEF为直角三角形.?
第3题图 第4题图 第6题图 第8题图
第9题图
第10题图
第15题图
第16题图
第18题图
第17题图
第20题图
第21题图
21世纪教育网 www.21CNjy.COM 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21CNjy.COM)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
