浙教版八年级数学下册第5章特殊平行四边形单元测试题含答案
文档属性
| 名称 | 浙教版八年级数学下册第5章特殊平行四边形单元测试题含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-29 00:00:00 | ||
图片预览




文档简介
第5章特殊平行四边形
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷30分,第Ⅱ卷70分, 共100分,考试时间90分钟.
第Ⅰ卷 (选择题 共30分)
一、选择题(本题有10小题,每小题3分,共30分)
1.矩形具有而一般平行四边形不具有的性质是 ( )
A. 对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.已知菱形两条对角线的长分别为6和8,则这个菱形的周长为 ( )
A. 18 B.20
C.22 D.24
3.四边形ABCD的对角线AC,BD相交于点O,不能判定它是矩形的条件是 ( )
A. AO=CO,BO=DO,AC=BD
B.AB∥CD,AB=CD,∠BAD=90°
C.∠BAD=∠ABC=90°,∠BCD+∠ADC=180°
D.∠BCD=∠ABC=∠ADC=90°
4.若矩形的一条对角线与一边的夹角是40°,则两条对角线所夹的锐角的度数为 ( )
A.80° B.60°
C.45° D.40°
5.如图1,在菱形ABCD中,∠B=60°,AB=4,则以AC为一边的正方形ACEF的周长为 ( )
图1
A. 14 B.15
C.16 D.17
6.如图2,矩形ABCD的周长为20 cm,两条对角线相交于点O,过点O作AC的垂线EF,与AD和BC分别交于点E,F,连结CE,则△CDE的周长为 ( )
图2
A. 5 cm B.8 cm C.9 cm D.10 cm
7.如图3,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是 ( )
图3
A. 48 B.60 C.76 D.80
8.若顺次连结四边形ABCD各边中点所得的四边形是矩形,则四边形ABCD一定是 ( )
A. 矩形 B.菱形
C.对角线互相垂直的四边形 D.对角线相等的四边形
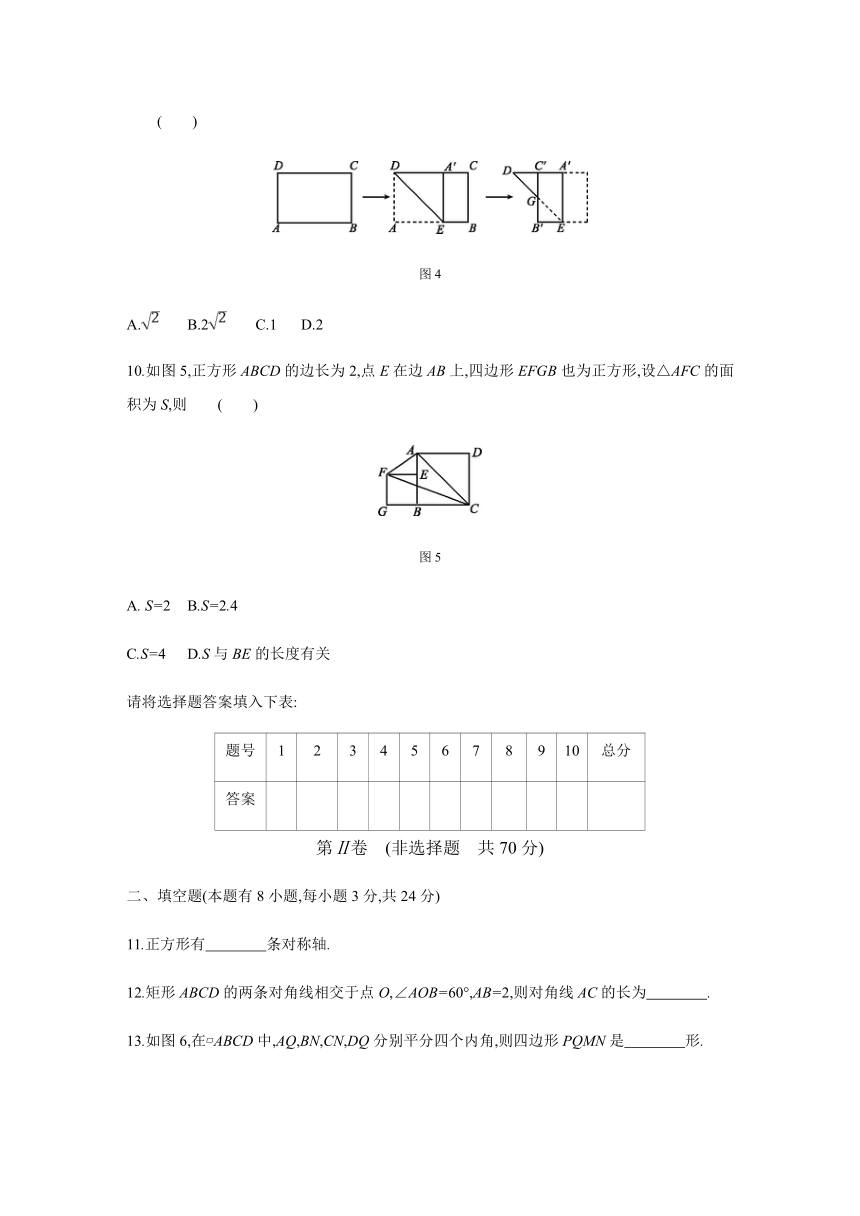
9.一张矩形纸片ABCD,已知AB=3,AD=2,小明按图4的步骤折叠纸片,则线段DG的长为 ( )
图4
A. B.2 C.1 D.2
10.如图5,正方形ABCD的边长为2,点E在边AB上,四边形EFGB也为正方形,设△AFC的面积为S,则 ( )
图5
A. S=2 B.S=2.4
C.S=4 D.S与BE的长度有关
请将选择题答案填入下表:
题号 1 2 3 4 5 6 7 8 9 10 总分
答案
第Ⅱ卷 (非选择题 共70分)
二、填空题(本题有8小题,每小题3分,共24分)
11.正方形有 条对称轴.?
12.矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则对角线AC的长为 .?
13.如图6,在?ABCD中,AQ,BN,CN,DQ分别平分四个内角,则四边形PQMN是 形.?
图6
14.如果菱形的两条对角线的长分别为a和b,且a,b满足(a-1)2+=0,那么菱形的面积等于 .?
15.如图7,延长正方形ABCD的边AB到点E,使BE=AC,则∠E= °.?
图7
16.如图8,在△ABC中,D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC.从中选择一个条件,使四边形BECF是菱形,你认为这个条件是 .(只填写序号)?
图8
17.如图9,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜边AB上的中线,将△BCD沿直线CD翻折至△ECD的位置,连结AE.若DE∥AC,则AE的长为 .?
图9
18.如图10①,有一张菱形纸片ABCD,BC=6,∠ABC=120°.先将其沿较短的对角线BD剪开,固定△DBC,并把△ABD沿着BC方向平移,得到△A'B'D'(点B在边BC上)如图②.当两个三角形重叠部分的面积为4时,它移动的距离BB'= .?
图10
三、解答题(本题有6小题,共46分)
19.(6分)已知:如图11,E是正方形ABCD的边CD上一点,F是CB的延长线上一点,且EA⊥AF.
求证:DE=BF.
图11
20.(6分)如图12,E,F分别为△ABC的边BC,AB的中点,延长EF到点D,使得DF=EF,连结DA,DB,AE.
(1)求证:四边形AEBD是平行四边形;
(2)若AB=AC,求证:四边形AEBD是矩形.
图12
21.(8分)如图13,将矩形ABCD沿BD对折,点A落在点E处,BE与CD相交于点F.若AD=3,BD=6.
(1)求证:△DEF≌△BCF;
(2)求∠EBC的度数.
图13
22.(8分)如图14,已知△ABC,按如下步骤作图:①分别以点A,C为圆心,以大于AC的长为半径在AC两侧作弧,交于两点M,N;②连结MN,与AB,AC分别交于点D,O;③过点C作CE∥AB交MN于点E,连结AE,CD.
求证:四边形ADCE是菱形.
图14
23.(8分)如图15,在菱形ABCD中,AB=2,∠DAB=60°,E是边AD的中点,M是边AB上一动点(不与点A重合),延长ME交射线CD于点N,连结MD,AN.
(1)求证:四边形AMDN是平行四边形.
(2)填空:①当AM的值为 时,四边形AMDN是矩形;?
②当AM的值为 时,四边形AMDN是菱形.?
图15
24.(10分)课本中,把长与宽之比为的矩形纸片称为标准纸.请思考并解决下列问题:
(1)将一张标准纸ABCD(AB
图16
(2)在一堂综合实践课上,小明尝试着将矩形纸片ABCD(AB
第二步:沿过点D的直线折叠,使点C落在边AD上的点N处,折痕为DG(如图17乙所示),此时点E恰好落在边AG上的点M处;
第三步:沿直线DM折叠(如图17丙所示),此时点G恰好与点N重合.
请你探究:矩形纸片ABCD是不是一张标准纸,请说明理由.
图17
(3)不难发现:将一张标准纸按图18所示一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=,第5次对开后所得标准纸的周长是多少?探索并直接写出第2019次对开后所得标准纸的周长.
图18
答案
1 A
2 B
3 C
4 A
5 C
6 D
7 C
8 C
9 A
10 A
11 4
12 4
13 矩
14 2
15 22.5
16 ③
17 2
18 2或4
19.证明:在正方形ABCD中,AB=AD,∠BAD=∠ABC=∠D=90°,∴∠ABF=∠D=90°.
∵EA⊥AF,∴∠FAB+∠BAE=90°.
∵∠BAE+∠EAD=90°,
∴∠FAB=∠EAD,∴△ABF≌△ADE,
∴DE=BF.
20.证明:(1)∵F为AB的中点,∴AF=BF.
∵DF=EF,
∴四边形AEBD是平行四边形.
(2)∵AB=AC,E是BC的中点,
∴AE⊥BC,∴∠AEB=90°.
由(1)知四边形AEBD为平行四边形,
∴四边形AEBD是矩形.
21.解:(1)证明:由折叠的性质和矩形的性质可得
DE=AD=BC,∠E=∠A=∠C=90°.
在△DEF和△BCF中,
∴△DEF≌△BCF(AAS).
(2)在Rt△ABD中,∵AD=3,BD=6,
∴∠ABD=30°.
由折叠的性质可得∠DBE=∠ABD=30°,
∴∠EBC=90°-30°-30°=30°.
22.证明:由题意可知直线DE是线段AC的垂直平分线,
∴AC⊥DE,AD=CD,AE=CE,AO=CO.
∴∠AOD=∠COE=90°.
又∵CE∥AB,∴∠ADO=∠CEO,
∴△AOD≌△COE,∴AD=CE,
∴AD=AE=CE=CD,
∴四边形ADCE是菱形.
23.解:(1)证明:∵四边形ABCD为菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME.
又∵E是边AD的中点,∴DE=AE,
∴△NDE≌△MAE,∴ND=AM,
∴四边形AMDN是平行四边形.
(2)①1 ②2
24.解:(1)证明:∵矩形纸片ABCD是标准纸,∴=.
由对开的含义知AF=AD,
∴==2·==,
∴矩形纸片ABEF也是标准纸.
(2)矩形纸片ABCD是一张标准纸.
理由如下:设AB=CD=a,由图形折叠的性质可知DN=CD=DG=a,DG⊥EM,∠DAG=∠ADG=45°,
∴△ADG是等腰直角三角形.
在Rt△ADG中,AD==a,
∴==,
∴矩形纸片ABCD是一张标准纸.
(3)
对开次数 第1次 第2次 第3次 第4次 第5次 …
周长 21+ 2+ 2+ 2+ 2+ …
∴第5次对开后所得标准纸的周长为,
第2019次对开后所得标准纸的周长为.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
