5.1~5.2 特殊平行四边形同步测试题(含答案)
文档属性
| 名称 | 5.1~5.2 特殊平行四边形同步测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-29 15:58:41 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版八下数学单元检测
特殊平行四边形5.1-5.2
选择题(每小题3分,共30分)
如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A. ∠ABC=90° B. AC=BD C. OA=OB D. OA=AD
2.如图,菱形花坛ABCD的对 角线BD=6,∠BAD=60°,则对角线AC的长为( )
A. B. 6 C. D. 3
3.下列说法中,错误的是( )
A.平行四边形的对角线互相平分 B.菱形的对角线互相垂直
C.矩形的对角线相等 D.矩形的对角线不可能垂直
4.如图,菱形ABCD的对角线AC、BD交于点O,E为AD边中点,若AB=7,则OE的长为( )
A. 3.5 B. 4 C. 7 D. 14
5.已知四边形ABCD是平行四边形,AC,BD是对角线,下列结论中不正确的是 ( )
A.当AB=BC时,它是菱形 B.当∠ABC=90°时,它是矩形
C.当∠ABD=∠CBD时,它是矩形 D.当AC⊥BD时,它是菱形
6.矩形的两条对角线所成的钝角为120°,若一条对角线的长是2,那么它的周长是(???)
A.6 B. C. D.
7.如图,已知E是菱形ABCD的边BC上一点,
且∠DAE=∠B=80°,那么∠CDE的大小为( )
A.20° B.25° C.30° D.35°
如图,菱形ABCD中,点M,N在AC上,ME⊥AD, NF⊥AB.
若NF = NM = 2,ME = 3,则AN 的长为( )
A.3 B.4 C.5 D.6
9.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
A.矩形 B.菱形 C.对角线相等的四边形 D.对角线互相垂直的四边形
10. 如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
A.甲正确,乙错误 B.乙正确,甲错误
C.甲、乙均正确 D.甲、乙均错误
二、填空题(每小题3分,共24分)
11.如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长是 .
12.如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 ,使ABCD成为菱形(只需添加一个即可)
13.如12题图,AC和BD是菱形ABCD的对角线,若∠BAC=70°,则 ∠DBC= °
14. 如图,矩形ABCD中,AD=2,对角线AC=,则BD=_______,∠AOB= °.
15. 如图,矩形一个角的平分线BE分矩形的边AD为2cm和3cm两部分,则这个矩形的面积是________.
16.如图,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AE平分∠BAD,AE交BC于E,则∠AEO的大小是_______________°.
17. 如图,在菱形ABCD中,对角线AC=6,BD=8,若过点A作AE⊥BC,垂足为E,则AE的长为?????????????????.
18.如图,在RtΔABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=?????? ???时,平行四边形CDEB为菱形.
?
解答题(共46分)
19.(本题6分)如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
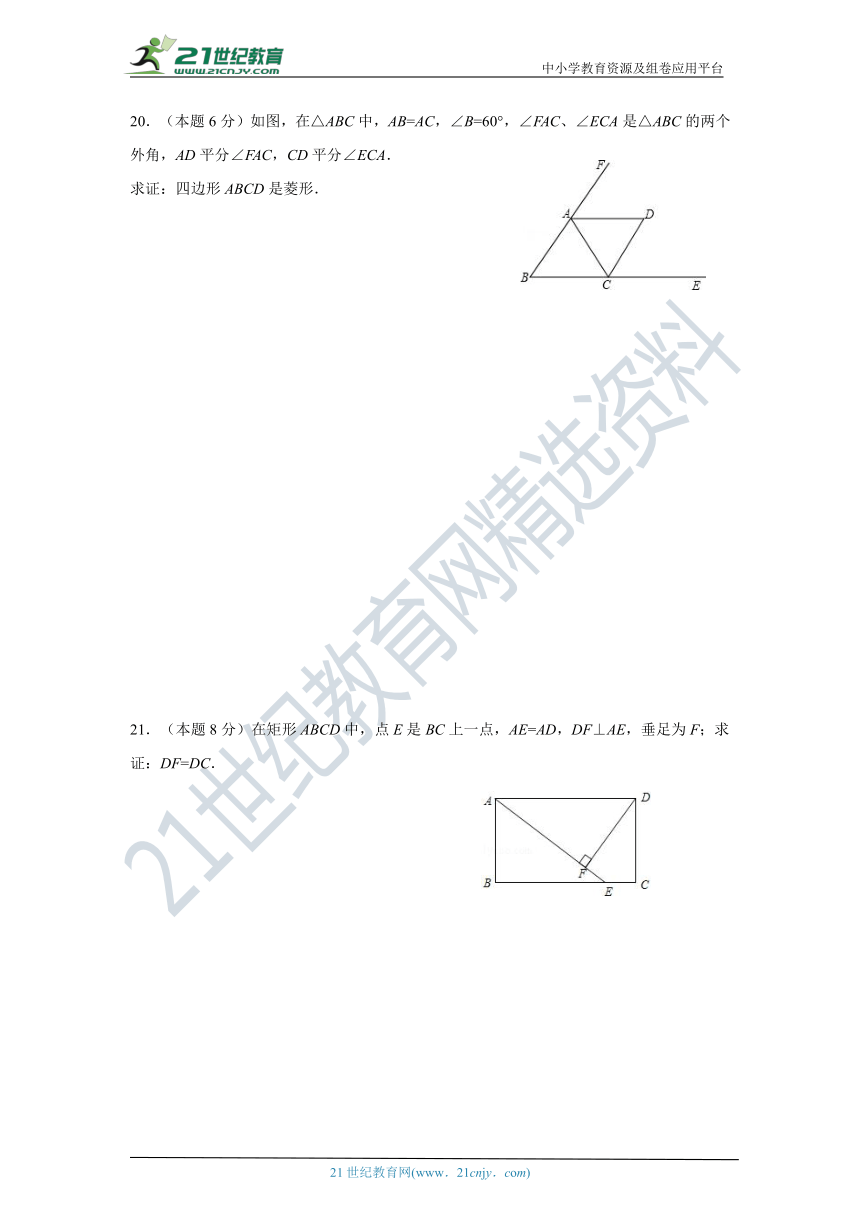
20.(本题6分)如图,在△ABC中,AB=AC,∠B=60°,∠FAC、∠ECA是△ABC的两个外角,AD平分∠FAC,CD平分∠ECA.
求证:四边形ABCD是菱形.
21.(本题8分)在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F;求证:DF=DC.
22.(本题8分)如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
23. (本题8分)已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
24. (本题10分)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
附加题:
25. (1)如图1,纸片□ABCD中,AD=5,S□ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′ 的位置,拼成四边形AEE′D,则四边形AEE′D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′ 的位置,拼成四边形AFF′D.
① 求证四边形AFF′D是菱形;
② 求四边形AFF′D两条对角线的长.
答案
一、选择题DADAC CCBDC
二、填空题:
11.6
12.如OA=OC
13.20°
14.,60°
15.15
16.30°
17.4.8
18.
三、解答题:
19. ∵四边形ABCD是矩形,∴∠A=∠B=90°,AD=BC,∵∠AOC=∠BOD,∴∠AOC﹣∠DOC=∠BOD﹣∠DOC,∴∠AOD=∠BOC,
∴△AOD≌△BOC,∴AO=OB.
20. ∵∠B=60°,AB=AC,∴△ABC为等边三角形,∴AB=BC,∴∠ACB=60°,∠FAC=∠ACE=
120°,∴∠BAD=∠BCD=120°,∴∠B=∠D=60°,∴四边形ABCD是平行四边形,
∵AB=BC,∴平行四边形ABCD是菱形.
21. 连接DE.∵AD=AE,∴∠AED=∠ADE.∵矩形ABCD,
∴AD∥BC,∠C=90°.∴∠ADE=∠DEC,∴∠DEC=∠AED.又∵DF⊥AE,∴∠DFE=∠C=90°.∵DE=DE,∴△DFE≌△DCE.∴DF=DC.
22. ∵四边形ABCD是矩形,∴∠MDO=∠NBO,∠DMO=∠BNO
???∵????MN是BD的垂直平分线????∴?DO=BO
∴?⊿DOM≌⊿BOM(AAS)∴?DM=BN,?∴四边形BMDN是平行四边形.?????????
又??????????所以,四边形是平行菱形.????
解:设MD=x, 则BM=MD=x,?????????
在Rt⊿AMB中,,,
23. 证明:∵DE∥AC,AE∥BD,∴四边形AODE是平行四边形,∵在菱形ABCD中,AC⊥BD,∴平行四边形AODE是菱形; (2)解:∵∠BCD=120°,AB∥CD,∴∠ABC=180°﹣120°=60°,∵AB=BC,∴△ABC是等边三角形,
∴OD=OB=,∴四边形AODE的面积=OA?OD=3×=
24. BD=CD.理由如下:依题意得AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,
∴AE=DE,∴△AEF≌△DEC(AAS),∴AF=CD,∵AF=BD,∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,∵AB=AC,BD=CD(三线合一),∴∠ADB=90°,
∴四边形AFBD是矩形.
25. (1) 由平移知:AEDE′, ∴四边形AEE′D是平行四边形,又AE⊥BC, ∴∠AEE′=90°,
∴四边形AEE′D是矩形,∴C选项正确. (2) ① ∵AFDF′, ∴四边形AFF′D是平行四边形,∵AE=3, EF=4 ,∠E=90°, ∴AF=5, ∵S□ABCD=AD·AE=15, ∴AD=5 , ∴AD=AF , ∴四边形AFF′D是菱形. ② 如下图, 连接AF′, DF ,在Rt△AEF′中, AE=3, EF′=9, ∴AF′=
在Rt△DFE′中, FE′=1, DE′=AE=3, ∴DF= ∴四边形AFF′D两条对角线的长分别是和.
第1题图 第2题图 第4题图 第6题图
第7题图
第8题图
第11题图 第12题图 第13题图 第14题图
第16题图 第17题图 第18题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
