浙教版数学八下2.4 一元二次方程根与系数的关系课件(20张PPT)
文档属性
| 名称 | 浙教版数学八下2.4 一元二次方程根与系数的关系课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 538.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-15 00:00:00 | ||
图片预览








文档简介
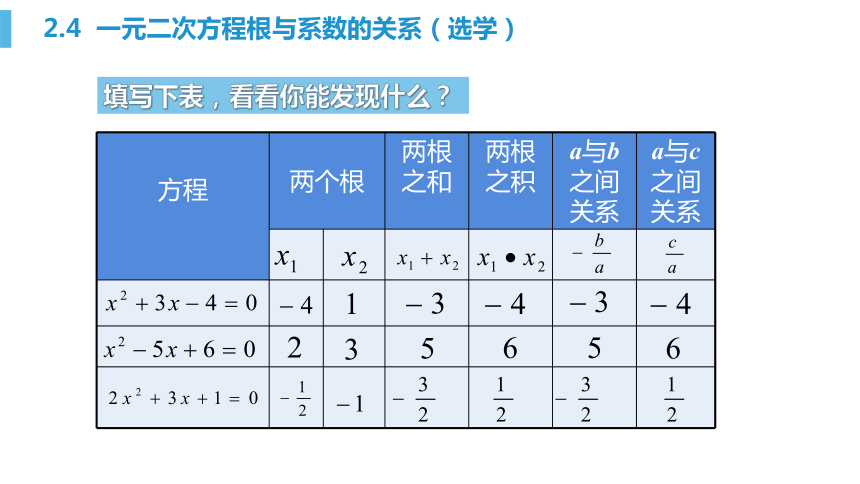
课件20张PPT。x(x-1)= 380第2章 一元二次方程2.4 一元二次方程根与系数的关系(选学)填写下表,看看你能发现什么?2.4 一元二次方程根与系数的关系(选学)这种关系是这几个方程所特有的还是对于任意的一元二次方程都适合的呢?我们来证明一下如果一元二次方程
的两个根分别是 , ,那么:能用这个结论的前提为△≥02.4 一元二次方程根与系数的关系(选学)证明:在2.4 一元二次方程根与系数的关系(选学)2.4 一元二次方程根与系数的关系(选学)韦达(1540-1603) 韦达是法国十六世纪最有影响的数学家之一。第一个引进系统的代数符号,并对方程论做了改进。 他生于法国的普瓦图。年青时学习法律当过律师,后从事政治活动,当过议会的议员,在对西班牙的战争中曾为政府破译敌军的密码。韦达还致力于数学研究,第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步。韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”)。 韦达在欧洲被尊称为“代数学之父”。 2.4 一元二次方程根与系数的关系(选学)利用根与系数的关系求方程的两根的和与积A2.4 一元二次方程根与系数的关系(选学)解 析2.4 一元二次方程根与系数的关系(选学)说出下列各方程的两根之和与两根之积:(1) x2 - 2x - 1=0(2) 2x2 - 6x =0x1+x2=2x1x2=-1x1+x2=3x1x2=02.4 一元二次方程根与系数的关系(选学)求:(1) (2)分析:求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.2.4 一元二次方程根与系数的关系(选学)解 答:总 结几种常见的求值:2.4 一元二次方程根与系数的关系(选学)例2:已知一个一元二次方程的二次项系数是3,它的两个根分别是 请写出这个方程。解:设这个方程为 ,由一元二次方程根与系数的关系,得2.4 一元二次方程根与系数的关系(选学)设x1,x2是方程2x2-9x+6=0的两个根,求下列各式的值:2.4 一元二次方程根与系数的关系(选学)2.4 一元二次方程根与系数的关系(选学)2.4 一元二次方程根与系数的关系(选学)周长是24,面积是92.4 一元二次方程根与系数的关系(选学)已知方程x2-(k+1)x+3k=0的一个根是2 ,求它的另一个根及k的值.(用两种方法解答)解法一:设方程的另一个根为x2.由根与系数的关系,得2+x2=k+1,2x2 = 3k解得x2 =-3 ,k =-2答:方程的另一个根是-3, k的值是-2.2.4 一元二次方程根与系数的关系(选学)已知方程x2-(k+1)x+3k=0的一个根是2 ,求它的另一个根及k的值。(用两种方法解答)解法二:设方程的另一个根为x2.把 x=2代入方程,得 4-2(k+1)+3k=0解这方程,得 k=-2由根与系数的关系,得2x2=3k即2x2=-6∴ x2=-3答:方程的另一个根是-3,k的值是-2.
谢 谢 观 看!
的两个根分别是 , ,那么:能用这个结论的前提为△≥02.4 一元二次方程根与系数的关系(选学)证明:在2.4 一元二次方程根与系数的关系(选学)2.4 一元二次方程根与系数的关系(选学)韦达(1540-1603) 韦达是法国十六世纪最有影响的数学家之一。第一个引进系统的代数符号,并对方程论做了改进。 他生于法国的普瓦图。年青时学习法律当过律师,后从事政治活动,当过议会的议员,在对西班牙的战争中曾为政府破译敌军的密码。韦达还致力于数学研究,第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步。韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”)。 韦达在欧洲被尊称为“代数学之父”。 2.4 一元二次方程根与系数的关系(选学)利用根与系数的关系求方程的两根的和与积A2.4 一元二次方程根与系数的关系(选学)解 析2.4 一元二次方程根与系数的关系(选学)说出下列各方程的两根之和与两根之积:(1) x2 - 2x - 1=0(2) 2x2 - 6x =0x1+x2=2x1x2=-1x1+x2=3x1x2=02.4 一元二次方程根与系数的关系(选学)求:(1) (2)分析:求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.2.4 一元二次方程根与系数的关系(选学)解 答:总 结几种常见的求值:2.4 一元二次方程根与系数的关系(选学)例2:已知一个一元二次方程的二次项系数是3,它的两个根分别是 请写出这个方程。解:设这个方程为 ,由一元二次方程根与系数的关系,得2.4 一元二次方程根与系数的关系(选学)设x1,x2是方程2x2-9x+6=0的两个根,求下列各式的值:2.4 一元二次方程根与系数的关系(选学)2.4 一元二次方程根与系数的关系(选学)2.4 一元二次方程根与系数的关系(选学)周长是24,面积是92.4 一元二次方程根与系数的关系(选学)已知方程x2-(k+1)x+3k=0的一个根是2 ,求它的另一个根及k的值.(用两种方法解答)解法一:设方程的另一个根为x2.由根与系数的关系,得2+x2=k+1,2x2 = 3k解得x2 =-3 ,k =-2答:方程的另一个根是-3, k的值是-2.2.4 一元二次方程根与系数的关系(选学)已知方程x2-(k+1)x+3k=0的一个根是2 ,求它的另一个根及k的值。(用两种方法解答)解法二:设方程的另一个根为x2.把 x=2代入方程,得 4-2(k+1)+3k=0解这方程,得 k=-2由根与系数的关系,得2x2=3k即2x2=-6∴ x2=-3答:方程的另一个根是-3,k的值是-2.
谢 谢 观 看!
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
