2020年浙教新版九年级下学期《2.2 切线长定理》同步练习卷解析版
文档属性
| 名称 | 2020年浙教新版九年级下学期《2.2 切线长定理》同步练习卷解析版 |
|
|
| 格式 | zip | ||
| 文件大小 | 539.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-21 00:00:00 | ||
图片预览

文档简介
2020年浙教新版九年级下学期《2.2 切线长定理》同步练习卷
一.选择题(共16小题)
1.如图,PA、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为( )
A.40° B.140° C.70° D.80°
2.如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为( )
A.120° B.60° C.30° D.45°
3.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( )
A.8 B.9 C.10 D.11
4.如图,PA、PB分别切⊙O于A、B,PA=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交PA、PB于点E、F.则△PEF的周长为( )
A.10cm B.15cm C.20cm D.25cm
5.如图,AD、AE、CB均为⊙O的切线,D、E、F分别为切点,AD=8,则△ABC的周长为( )
A.8 B.10 C.12 D.16
6.如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有( )个
①AF=BG②CG=CH③AB+CD=AD+BC④BG<CG.
A.1 B.2 C.3 D.4
7.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C,且在上的动点,则∠BPC的度数是( )
A.65° B.115° C.115°或65° D.130°或65°
8.如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C.4 D.8
9.如图所示,PA,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是( )
A.PA=PB B.∠APO=20° C.∠OBP=70° D.∠AOP=70°
10.如图,AE、AD和BC分别切⊙O于点E、D、F,如果AD=20,则△ABC的周长为( )
A.20 B.30 C.40 D.50
11.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C. D.
12.如图,圆O的圆心在梯形ABCD的底边AB上,并与其它三边均相切,若AB=10,AD=6,则CB长( )
A.4 B.5 C.6 D.无法确定
13.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为( )
A.50 B.52 C.54 D.56
14.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为( )
A.5 B.10 C.7.5 D.4
15.已知⊙O的半径是4,P是⊙O外的一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB=( )
A.4 B. C. D.
16.如图,PA、PB分别切⊙O于A、B两点,如果∠P=60°,PA=2,那么AB的长为( )
A.1 B.2 C.3 D.4
二.填空题(共4小题)
17.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为 .
18.如图,菱形ABCD,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径为 .
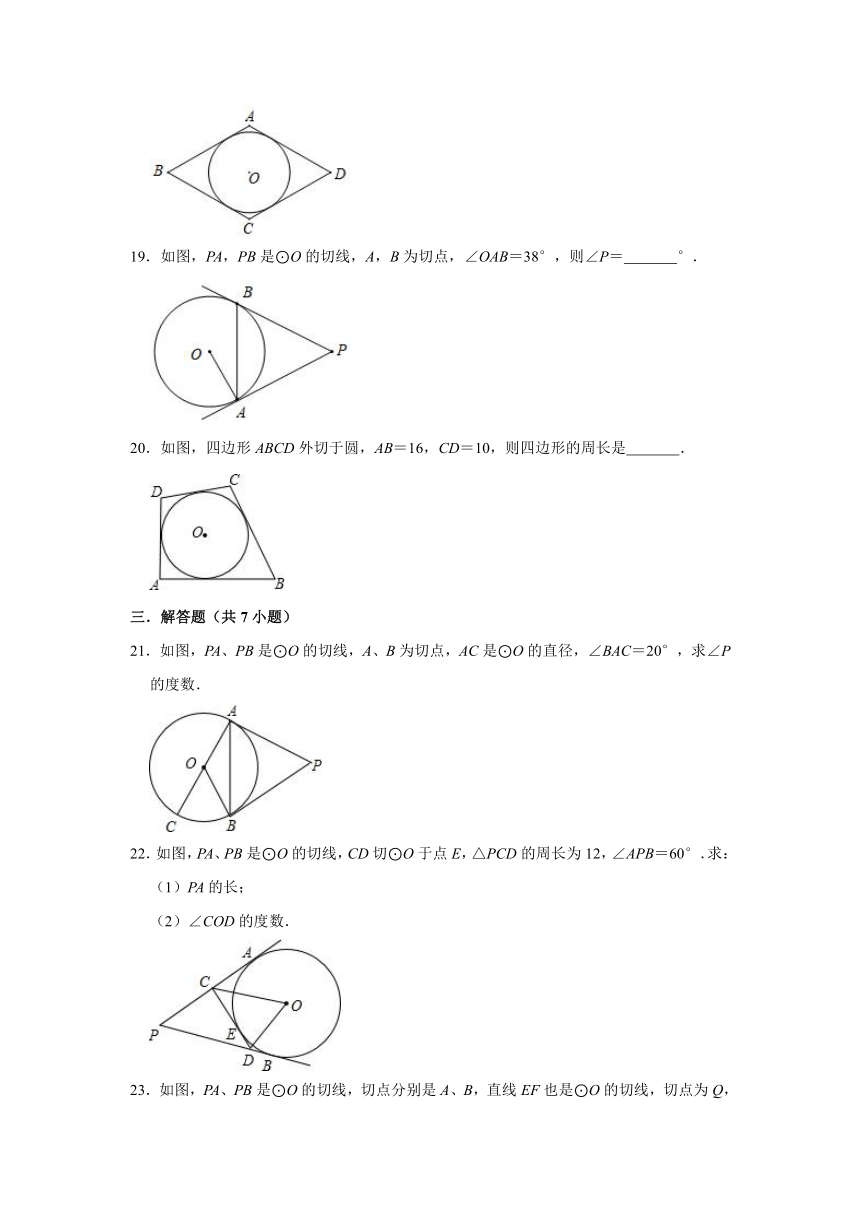
19.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P= °.
20.如图,四边形ABCD外切于圆,AB=16,CD=10,则四边形的周长是 .
三.解答题(共7小题)
21.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.
22.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
23.如图,PA、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交PA、PB于点E、F,已知PA=12cm,∠P=40°
①求△PEF的周长;
②求∠EOF的度数.
24.如图,PA、PB、DE切⊙O于点A、B、C、D在PA上,E在PB上,
(1)若PA=10,求△PDE的周长.
(2)若∠P=50°,求∠O度数.
25.如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
26.已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12cm,求△PEF的周长.
27.如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
(Ⅰ)求∠P的大小;
(Ⅱ)若AB=2,求PA的长(结果保留根号).
参考答案与试题解析
一.选择题(共16小题)
1.如图,PA、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为( )
A.40° B.140° C.70° D.80°
【分析】连接OA,OB根据切线的性质定理,切线垂直于过切点的半径,即可求得∠OAP,∠OBP的度数,根据四边形的内角和定理即可求的∠AOB的度数,然后根据圆周角定理即可求解.
【解答】解:∵PA是圆的切线.
∴∠OAP=90°,
同理∠OBP=90°,
根据四边形内角和定理可得:
∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣40°=140°,
∴∠ACB=∠AOB=70°.
故选:C.
2.如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为( )
A.120° B.60° C.30° D.45°
【分析】连接OA,BO,由圆周角定理知可知∠AOB=2∠E=120°,PA、PB分别切⊙O于点A、B,利用切线的性质可知∠OAP=∠OBP=90°,根据四边形内角和可求得∠P=180°﹣∠AOB=60°.
【解答】解:连接OA,BO;
∵∠AOB=2∠E=120°,
∴∠OAP=∠OBP=90°,
∴∠P=180°﹣∠AOB=60°.
故选:B.
3.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( )
A.8 B.9 C.10 D.11
【分析】根据圆外切四边形的性质对边和相等进而得出AD的长.
【解答】解:∵⊙O内切于四边形ABCD,
∴AD+BC=AB+CD,
∵AB=10,BC=7,CD=8,
∴AD+7=10+8,
解得:AD=11.
故选:D.
4.如图,PA、PB分别切⊙O于A、B,PA=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交PA、PB于点E、F.则△PEF的周长为( )
A.10cm B.15cm C.20cm D.25cm
【分析】根据切线长定理由PA、PB分别切⊙O于A、B得到PB=PA=10cm,由于过点C的切线分别交PA、PB于点E、F,再根据切线长定理得到EA=EC,FC=FB,然后三角形周长的定义得到△PEF的周长=PE+EF+PF=PE+EC+FC+PF,用等线段代换后得到三角形PEF的周长等于PA+PB.
【解答】解:∵PA、PB分别切⊙O于A、B,
∴PB=PA=10cm,
∵EA与EC为⊙的切线,
∴EA=EC,
同理得到FC=FB,
∴△PEF的周长=PE+EF+PF=PE+EC+FC+PF
=PE+EA+FB+PF
=PA+PB
=10+10
=20(cm).
故选:C.
5.如图,AD、AE、CB均为⊙O的切线,D、E、F分别为切点,AD=8,则△ABC的周长为( )
A.8 B.10 C.12 D.16
【分析】由AD、AE、CB均为⊙O的切线,D、E、F分别为切点,根据切线长定理,可得CE=CF,BD=BF,AE=AD=8,继而可求得△ABC的周长为AE+AD的和.
【解答】解:∵AD、AE、CB均为⊙O的切线,D、E、F分别为切点,
∴CE=CF,BD=BF,AE=AD=8,
∴△ABC的周长为:AC+BC+AB=AC+CF+BF+AB=AC+CE+BD+AB=AE+AD=16.
故选:D.
6.如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有( )个
①AF=BG②CG=CH③AB+CD=AD+BC④BG<CG.
A.1 B.2 C.3 D.4
【分析】根据切线长定理(从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角)对以下选项进行分析.
【解答】解:如图,连接OE、OF、OH、OG.
①∵⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,
∴BF=BG、AF=AE,
只有当点F是边AB的中点时,AF=BF=BG,否则,等式AF=BG不成立;
故本选项不一定正确;
②根据题意,知,CG、CH都是⊙O的切线,
∴CG=CH.
故本选项正确;
③根据题意,知
AF=AE,DH=DE,BF=BG,CG=CH,
则AF+BF+CH+DH=AE+BG+CG+DE,即AB+CD=AD+BC.
故本选项正确;
④当点G是边BC的中点时,BG=CG.
故本选项错误;
综上所述,正确的说法有2个;
故选:B.
7.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C,且在上的动点,则∠BPC的度数是( )
A.65° B.115° C.115°或65° D.130°或65°
【分析】连接OB、OC,根据四边形的内角和定理,求得∠BOC=130°,再由圆周角定理求得∠P的度数即可.
【解答】解:如图,连接OB、OC,
∵AB、AC是⊙O的切线,
∴∠OBA=∠OCA=90°,
∵∠A=50°,
∴∠BOC=130°,
∵∠BOC=2∠P,
∴∠BPC=65°;
故选:AC.
8.如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C.4 D.8
【分析】根据切线长定理和等边三角形的判定方法,发现等边三角形即可求解.
【解答】解:∵PA,PB分别切⊙O于点A、B,
∴PA=PB,
又∠P=60°,
∴△APB是等边三角形,
∴AB=PA=8.
故选:B.
9.如图所示,PA,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是( )
A.PA=PB B.∠APO=20° C.∠OBP=70° D.∠AOP=70°
【分析】根据切线长定理得A,B是正确的;再根据切线的性质定理以及直角三角形的两个锐角互余得D是正确的;根据切线的性质定理得C错误.
【解答】解:∵PA,PB是⊙O的切线,且∠APB=40°,
∴PA=PB,∠APO=∠BPO,∠A=∠B=90°,
∴∠OBP=∠OAP,
∴C是错误的.
故选:C.
10.如图,AE、AD和BC分别切⊙O于点E、D、F,如果AD=20,则△ABC的周长为( )
A.20 B.30 C.40 D.50
【分析】根据切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,将△ABC的周长转化为切线长求解.
【解答】解:据切线长定理有AD=AE,BE=BF,CD=CF;
则△ABC的周长=AB+BC+AC
=AB+BF+CF+AC
=AB+BE+AC+CD
=AD+AE=2AD
=40.
故选:C.
11.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C. D.
【分析】根据切线长定理知PA=PB,而∠P=60°,所以△PAB是等边三角形,由此求得弦AB的长.
【解答】解:∵PA、PB都是⊙O的切线,
∴PA=PB,
又∵∠P=60°,
∴△PAB是等边三角形,即AB=PA=8,
故选:B.
12.如图,圆O的圆心在梯形ABCD的底边AB上,并与其它三边均相切,若AB=10,AD=6,则CB长( )
A.4 B.5 C.6 D.无法确定
【分析】方法1、设圆O的半径是R,圆O与AD、DC、CB相切于点E、F、H,连接OE、OD、OF、OC、OH,则圆的半径R,可以看作△BOC,△COD,△AOD的高,根据S梯形ABCD=S△BOC+S△COD+S△DOA,以及梯形的面积公式即可求解.
方法2、利用切线的性质得出∠ADO=∠ODC,进而得出∠ADO=∠AOD,即可得出OA=6,即:OB=4,同理:BC=OB即可得出结论.
【解答】解:方法1、
设圆O的半径是R,圆O与AD、DC、CB相切于点E、F、H,连接OE、OD、OF、OC、OH.
设CD=y,CB=x.
设S梯形ABCD=S
则S=(CD+AB)R=(y+10)R﹣﹣﹣﹣(1)
S=S△BOC+S△COD+S△DOA
=xR+yR+×6R﹣﹣﹣﹣(2)
联立(1)(2)得x=4;
方法2、连接OD.OC
∵AD,CD是⊙O的切线,
∴∠ADO=∠ODC,
∵CD∥AB,
∴∠ODC=∠AOD,
∴∠ADO=∠AOD
∴AD=OA
∵AD=6,
∴OA=6,
∵AB=10,
∴OB=4,
同理可得
OB=BC=4,
故选:A.
13.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为( )
A.50 B.52 C.54 D.56
【分析】根据切线长定理,可以证明圆外切四边形的性质:圆外切四边形的两组对边和相等,从而可求得四边形的周长.
【解答】解:由题意可得圆外切四边形的两组对边和相等,
所以四边形的周长=2(16+10)=52.
故选:B.
14.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为( )
A.5 B.10 C.7.5 D.4
【分析】由切线长定理,可知:AF=AD,CF=CE,BE=BD,用未知数设AF的长,然后表示出BD、CF的长,即可表示出BE、CE的长,根据BE+CE=5,可求出AF的长.
【解答】解:设AF=x,根据切线长定理得AD=x,BD=BE=9﹣x,CE=CF=CA﹣AF=6﹣x,
则有9﹣x+6﹣x=5,解得x=5,即AF的长为5.
故选:A.
15.已知⊙O的半径是4,P是⊙O外的一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB=( )
A.4 B. C. D.
【分析】在Rt△POA中,用勾股定理,可求得PA的长,进而可根据∠APO的正弦值求出AC的长,即可求出AB的长.
【解答】解:如图所示,PA、PB切⊙O于A、B,
因为OA=4,PO=8,
则AP==4,∠APO=30°,
∵∠APB=2∠APO=60°
故△PAB是等边三角形,AB=AP=4
故选:C.
16.如图,PA、PB分别切⊙O于A、B两点,如果∠P=60°,PA=2,那么AB的长为( )
A.1 B.2 C.3 D.4
【分析】由切线长定理知PA=PB,根据已知条件即可判定△PAB是等边三角形,由此可求得AB的长.
【解答】解:∵PA、PB分别切⊙O于A、B,
∴PA=PB;
∵∠P=60°,
∴△PAB是等边三角形;
∴AB=PA=2,故选B.
二.填空题(共4小题)
17.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为 50 .
【分析】根据切线长定理得到AE=AH,BE=BF,CF=CG,DH=DG,得到AD+BC=AB+CD=25,根据四边形的周长公式计算,得到答案.
【解答】解:∵四边形ABCD是⊙O的外切四边形,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=25,
∴四边形ABCD的周长=AD+BC+AB+CD=25+25=50,
故答案为:50.
18.如图,菱形ABCD,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径为 .
【分析】作辅助线,构建直角△AOB,分别计算OA、OB的长,根据面积法可得OE的长.
【解答】解:设AB和BC上的切点分别为E、F,连接OA、OE、OB、OF,则OE⊥AB,OF⊥BC,
∵⊙O内切于菱形ABCD,
∴OE=OF,
∴OB平分∠ABC,
∵∠ABC=60°,
∴∠ABO=30°,
同理得∠BAO=60°,
∴∠AOB=90°,
∴AO=AB=2,OB=2,
∴S△AOB=AB?OE=AO?OB,
4OE=2×,
OE=,
故答案为:.
19.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P= 76 °.
【分析】由切线的性质得出PA=PB,PA⊥OA,得出∠PAB=∠PBA,∠OAP=90°,由已知得出∠PBA=∠PAB=90°﹣∠OAB=52°,再由三角形内角和定理即可得出结果.
【解答】解:∵PA,PB是⊙O的切线,
∴PA=PB,PA⊥OA,
∴∠PAB=∠PBA,∠OAP=90°,
∴∠PBA=∠PAB=90°﹣∠OAB=90°﹣38°=52°,
∴∠P=180°﹣52°﹣52°=76°;
故答案为:76.
20.如图,四边形ABCD外切于圆,AB=16,CD=10,则四边形的周长是 52 .
【分析】利用圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,即可得.
【解答】解:由题意可得圆外切四边形的两组对边和相等,
所以四边形的周长=2(16+10)=52.
故答案为:52.
三.解答题(共7小题)
21.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.
【分析】根据切线长定理得等腰△PAB,运用三角形内角和定理求解即可.
【解答】解:根据切线的性质得:∠PAC=90°,
所以∠PAB=90°﹣∠BAC=90°﹣20°=70°,
根据切线长定理得PA=PB,
所以∠PAB=∠PBA=70°,
所以∠P=180°﹣70°×2=40°.
22.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
【分析】(1)可通过切线长定理将相等的线段进行转换,得出三角形PDE的周长等于PA+PB的结论,即可求出PA的长;
(2)根据三角形的内角和求出∠ADC和∠BEC的度数和,然后根据切线长定理,得出∠EDO和∠DEO的度数和,再根据三角形的内角和求出∠DOE的度数.
【解答】解:(1)∵CA,CE都是圆O的切线,
∴CA=CE,
同理DE=DB,PA=PB,
∴三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°﹣120°=240°,
∵CA,CE是圆O的切线,
∴∠OCE=∠OCA=∠ACD;
同理:∠ODE=∠CDB,
∴∠OCE+∠ODE=(∠ACD+∠CDB)=120°,
∴∠COD=180﹣120°=60°.
23.如图,PA、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交PA、PB于点E、F,已知PA=12cm,∠P=40°
①求△PEF的周长;
②求∠EOF的度数.
【分析】①根据切线长定理得出PA=PB,EB=EQ,FQ=FA,由PE+EF+PF=PE+EQ+FQ+PF即可求出答案.
②连接OE,OF,求出∠OEF+∠OFE的度数,即可得出∠EOF的度数.
【解答】解:①∵PA、PB是⊙O的切线,
∴PA=PB,
又∵直线EF是⊙O的切线,
∴EB=EQ,FQ=FA,
∴△PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm;
②连接OE,OF,则OE平分∠BEF,OF平分∠AFE,
则∠OEF+∠OFE=(∠P+∠PFE)+∠(P+∠PEF)=(180°+40°)=110°,
∴∠EOF=180°﹣110°=70°.
24.如图,PA、PB、DE切⊙O于点A、B、C、D在PA上,E在PB上,
(1)若PA=10,求△PDE的周长.
(2)若∠P=50°,求∠O度数.
【分析】(1)于PA、PB、DE都是⊙O的切线,可根据切线长定理将切线PA、PB的长转化为△PDE的周长;
(2)连接OA、OC、0B,利用切线长定理即可得到∠O=∠AOB,根据四边形的内角和可得∠AOB+∠P=180°,进而求出∠O的度数.
【解答】解:(1)∵PA、PB、DE分别切⊙O于A、B、C,
∴PA=PB,DA=DC,EC=EB;
∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=10+10=20;
∴△PDE的周长为20;
(2)连接OA、OC、0B,
∵OA⊥PA,OB⊥PB,OC⊥DE,
∴∠DAO=∠EBO=90°,
∴∠P+∠AOB=180°,
∴∠AOB=180°﹣50°=130°
∵∠AOD=∠DOC,∠COE=∠BOE,
∴∠DOE=∠AOB=×130°=65°.
25.如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
【分析】(1)根据切线长定理推出AP=BP,根据等腰三角形性质和三角形的内角和定理求出∠PAB=60°,求出∠PAO=90°即可;
(2)根据直角三角形性质求出OP,根据勾股定理求出AP,根据等边三角形的判定和性质求出即可.
【解答】解:(1)∵PA,PB是⊙O的切线,
∴AP=BP,
∵∠P=60°,
∴∠PAB=60°,
∵AC是⊙O的直径,
∴∠PAC=90°,
∴∠BAC=90°﹣60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,
∴OP=4,
由勾股定理得:,
∵AP=BP,∠APB=60°,
∴△APB是等边三角形,
∴.
26.已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12cm,求△PEF的周长.
【分析】根据切线长定理得出PA=PB,EB=EQ,FQ=FA,代入PE+EF+PF=PE+EQ+FQ+PF即可求出答案.
【解答】解:∵PA、PB是⊙O的切线,切点分别是A、B,
∴PA=PB=12,
∵过Q点作⊙O的切线,交PA、PB于E、F点,
∴EB=EQ,FQ=FA,
∴△PEF的周长是:PE+EF+PF=PE+EQ+FQ+PF,
=PE+EB+PF+FA=PB+PA=12+12=24,
答:△PEF的周长是24.
27.如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
(Ⅰ)求∠P的大小;
(Ⅱ)若AB=2,求PA的长(结果保留根号).
【分析】(Ⅰ)根据切线的性质及切线长定理可证明△PAC为等边三角形,则∠P的大小可求;
(Ⅱ)由(Ⅰ)知PA=PC,在Rt△ACB中,利用30°的特殊角度可求得AC的长.
【解答】解:(Ⅰ)∵PA是⊙O的切线,AB为⊙O的直径,
∴PA⊥AB,
∴∠BAP=90°;
∵∠BAC=30°,
∴∠CAP=90°﹣∠BAC=60°.
又∵PA、PC切⊙O于点A、C,
∴PA=PC,
∴△PAC为等边三角形,
∴∠P=60°.
(Ⅱ)如图,连接BC,则∠ACB=90°.
在Rt△ACB中,AB=2,∠BAC=30°,
∵cos∠BAC=,
∴AC=AB?cos∠BAC=2cos30°=.
∵△PAC为等边三角形,
∴PA=AC,
∴PA=.
