第三章 投影与三视图单元测试卷A(含解析)
文档属性
| 名称 | 第三章 投影与三视图单元测试卷A(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-22 14:22:41 | ||
图片预览




文档简介
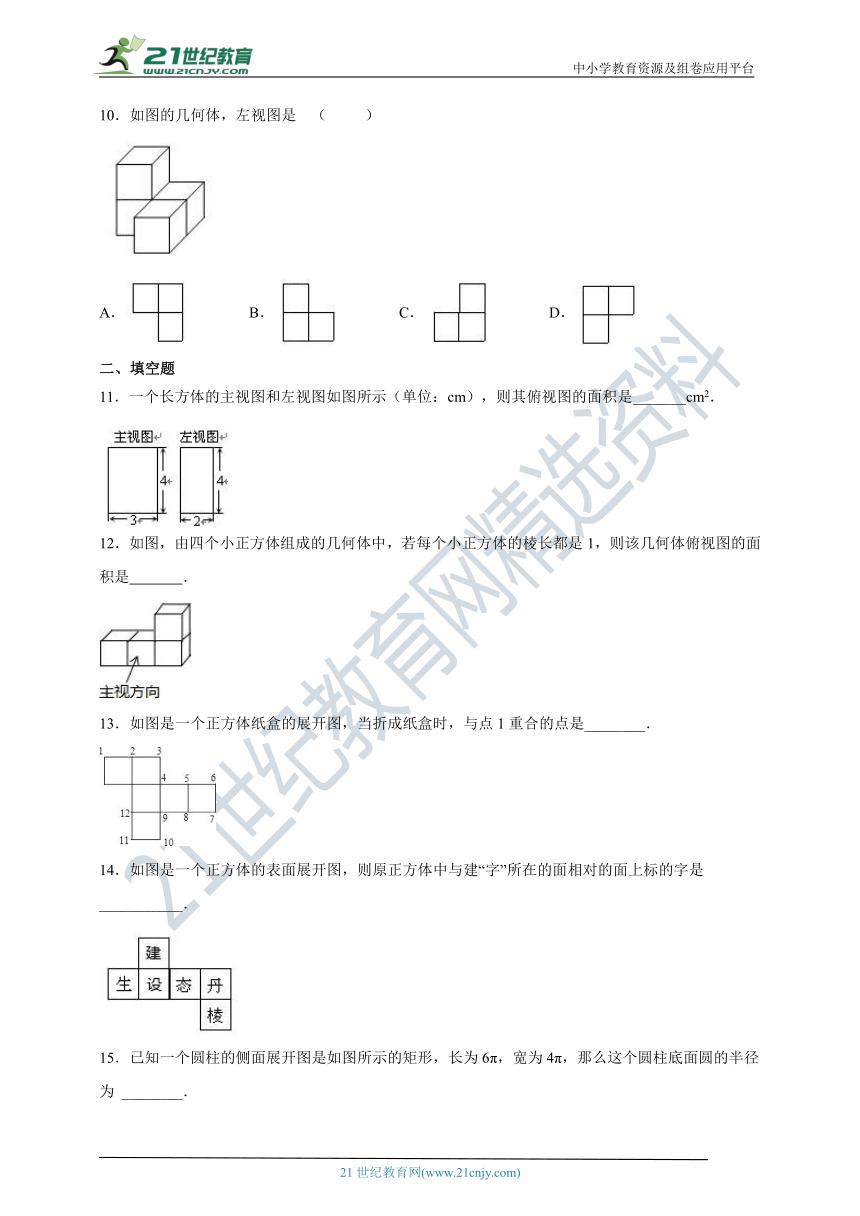
投影与三视图单元测试卷(A)
一、单选题
1.一物体及其正视图如下图所示,则它的左视图与俯视图分别是右侧图形中的( ).
A.①② B.③④ C.①④ D.③②
2.如图,从左面观察这个立体图形,能得到的平面图形是( ???)
A.B.C.D.
3.明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )
?
A.? B.? C.? D.?
4.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是(??? )
A.108cm3 B.100 cm3 C.92cm3 D.84cm3
5.长方体的主视图、俯视图如图所示,则长方体的表面积为( )
A.12 B.19 C.24 D.38
6.下面四个立体图形中,主视图是三角形的是( )
A. B. C. D.
7.下列四个几何体:
其中左视图与俯视图相同的几何体共有( )
A.1个 B.2个 C.3个 D.4个
8.如图是一个由4个相同的正方体组成的立体图形,它的主视图是(?? )
A. B. C. D.
9.如图,一个由6个大小相同、棱长为1的正方体搭成的几何体,下列关于这个几何体的说法正确的是( )
A.主视图的面积为6 B.左视图的面积为2
C.俯视图的面积为4 D.俯视图的面积为3
10.如图的几何体,左视图是 ( )
A. B. C. D.
二、填空题
11.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是_______cm2.
12.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .
13.如图是一个正方体纸盒的展开图,当折成纸盒时,与点1重合的点是________.
14.如图是一个正方体的表面展开图,则原正方体中与建“字”所在的面相对的面上标的字是___________.
15.已知一个圆柱的侧面展开图是如图所示的矩形,长为6π,宽为4π,那么这个圆柱底面圆的半径为 ________.
16.由两个长方体组合而成的一个立体图形,从两个不同的方向看得到的形状图如图所示,根据图中所标尺寸(单位:mm)可知这两个长方体的体积之和是____________mm3.
三、解答题
17.用相同的小立方体搭一个几何体,从正面、上面看到的形状图如图所示,从上面看到的形状图中小正方形的字母表示在该位置上小立方体的个数,请回答下列问题:
(1)a,b,c各表示的数字是几?
(2)这个几何体最多由几个小立方体搭成?最少呢?
(3)当,时,画出这个几何体从左面看得到的形状图.
18.如图是位于陕西省西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度,由于观测点与小雁塔底部间的距离不易测量,因此经过研究需要进行两次测量,于是在阳光下,他们首先利用影长进行测量,方法如下:小铭在小雁塔的影子顶端D处竖直立一根木棒CD,并测得此时木棒的影长DE=2.4米;然后,小希在BD的延长线上找出一点F,使得A、C、F三点在同一直线上,并测得DF=2.5米.已知图中所有点均在同一平面内,木棒高CD=1.72米,AB⊥BF,CD⊥BF,试根据以上测量数据,求小雁塔的高度AB.
19.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
20.如图,圆锥的底面半径为10 cm,高为10cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥侧面一周回到SA上的点M处,且SM=3AM,求它所走的最短距离.
21.已知图为一几何体从不同方向看的图形:
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若长方形的高为10厘米,三角形的边长为4厘米,求这个几何体的侧面积.
22.如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请画出添加小正方体后所得几何体可能的左视图.
23.如图,边长为acm的正方体其上下底面的对角线AC、A1C1与平面H垂直.
(1)指出正方体在平面H上的正投影图形;
(2)计算投影MNP的面积.
24.画出如图所示图形从正面、从左面和从上面看到的形状图.
参考答案
1.D【解析】先细心观察原立体图形和俯视图中两个长方体的位置关系,从几何体的左边看去是2个长方体叠在一起,所以左视图是③,从上面看下来是3个长方体并排,所以俯视图是②.
故选D.
2.A【解析】从左面看下面一个正方形,上面一个正方形,故选A.
3.B【解析】根据展开图中各种符号的特征和位置,可得墨水在B盒子里面.
故选B.
4.B
【解析】由题意得,该几何体的体积是:6×6×3-×42×3=100.故选B.
5.D【解析】由主视图可得长方体的长为4,高为1,
由俯视图可得长方体的宽为3,则这个长方体的表面积是(4×1+4×3+3×1)×2
=19×2=38.故这个长方体的表面积是38.故选D.
6.C【解析】
A、主视图为长方形,不符合题意;
B、主视图为圆,不符合题意;
C、主视图为三角形,符合题意;
D、主视图为长方形,不符合题意;
故选C.
7.B【解析】正方体左视图、俯视图都是正方形,左视图与俯视图相同;
球左视图、俯视图都是圆,左视图与俯视图相同;
圆锥左视图、俯视图分别是三角形、有圆心的圆,左视图与俯视图不相同;
圆柱左视图、俯视图分别是长方形、圆,左视图与俯视图不相同;
即同一个几何体的左视图与俯视图相同的几何体共有2个.
故选B.
8.A【解析】从正面看易得第一层有2个正方形,第二层左边有一个正方形,第三层左边有一个正方形.故选:A.
9.C【解析】
A. 从主视图看,可以看到5个面,故本选项错误;
B. 从左视图看,可以看到3个面,故本选项错误;
C. 从俯视图看,可以看到4个面,故本选项正确;
D. 由以上判断可知,故本选项错误;故选C.
10.B【解析】从左边看去,左边是两个正方形,右边是一个正方形.故选B.
11.6【解析】一个长方体的主视图和左视图如图所示,这个长方体的高是4,底面长是3,底面宽是2;长方体的俯视图就是其底面的图形,是长是3,宽是2的长方形,它的面积==6
12.3.【解析】试题分析:根据从上面看得到的图形是俯视图,可得俯视图,根据矩形的面积公式,可得答案:从上面看三个正方形组成的矩形,矩形的面积为1×3=3.
13.7和11
【解析】由正方体展开图的特征得出,折叠成正方体后,点1所在的正方形分别和点7、点11所在的两个正方形相交,
故点1与点7、点11重合.
故答案为7和11.
14.棱【解析】正方体的表面展开图中,相对的面一定隔着一个正方形.
“设”与“丹”是相对面,
“生”与“态”是相对面,
“建”与“棱”是相对面。
故答案为:棱.
15.2或3
【解析】(1)当底面圆的周长为6π时,底面圆的半径为6π÷π÷2=3;
(2)当底面圆的周长为4π时,底面圆的半径为4π÷π÷2=2.
故答案为2或3.
16.128
【解析】下面的长方体:2.
上面的长方体:432.
两个长方体的体积之和:96+32=128.
17.(1),,;(2)最多由11个小立方体搭成;最少由9个小立方体搭成;(3)见解析.
【解析】(1),,;
(2)(个),(个).
这个几何体最多由11个小立方体搭成;最少由9个小立方体搭成.
(3)如图所示.
18.43米.
【解析】由题意得:∠ABD=∠CDE=90°,∠ADB=∠CED,∴△CDE∽△ABD,∴=.
∵∠F=∠F,∴△CDF∽△ABF,∴=,∴=,即=,∴BD=60,∴=,∴AB=43.答:小雁塔的高度AB是43米.
19.(1)8;(2)答案见解析:(3)200000立方厘米
【解析】(1)小明共剪了8条棱,故答案为8.
(2)如图,四种情况.
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长高为acm,则长与宽相等为5acm,
∵长方体纸盒所有棱长的和是880cm,
∴4(a+5a+5a)=880,解得a=20cm,
∴这个长方体纸盒的体积为:20×100×100=200000cm3.
20.(1)500π;(2)50 cm.
【解析】(1)由题意,可得圆锥的母线SA===40(cm),
∴S侧=π×10×40=400π(cm2),S底=πAO2=100π(cm2),
∴S全=S侧+S底=(400+100)π=500π(cm2).
(2)沿母线SA将圆锥的侧面展开,如图,
则线段AM的长就是蚂蚁所走的最短距离.
由(1)知,SA=40 cm,=20π cm.
∵=20π(cm),
∴n==90,
∴∠S=90°.
∵SA′=SA=40 cm,SM=3A′M,
∴SM=30 cm,
∴在Rt△ASM中,由勾股定理得AM=50 cm,
∴蚂蚁所走的最短距离是50 cm.
21.三棱柱;(2)见解析;(3)
【解析】三棱柱;如图所示:
.
.
22.(1)作图见解析;(2)作图见解析.
【解析】解:(1)如图所示:
;
(2)添加后可得如图所示的几何体:
,
左视图分别是:
23.(1)矩形;(2)
【解析】(1)正方体在平面H上的正投影图形是矩形;
(2)∵正方体边长为acm,∴BD==(cm),∴投影MNPQ的面积为=(cm2).
24.如图所示见解析.
【解析】如图所示:
试卷第1页,总3页
试卷第1页,总3页
