第三章 投影与三视图单元测试卷B(含解析)
文档属性
| 名称 | 第三章 投影与三视图单元测试卷B(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-22 00:00:00 | ||
图片预览



文档简介
投影与三视图单元测试卷(B)
一、单选题
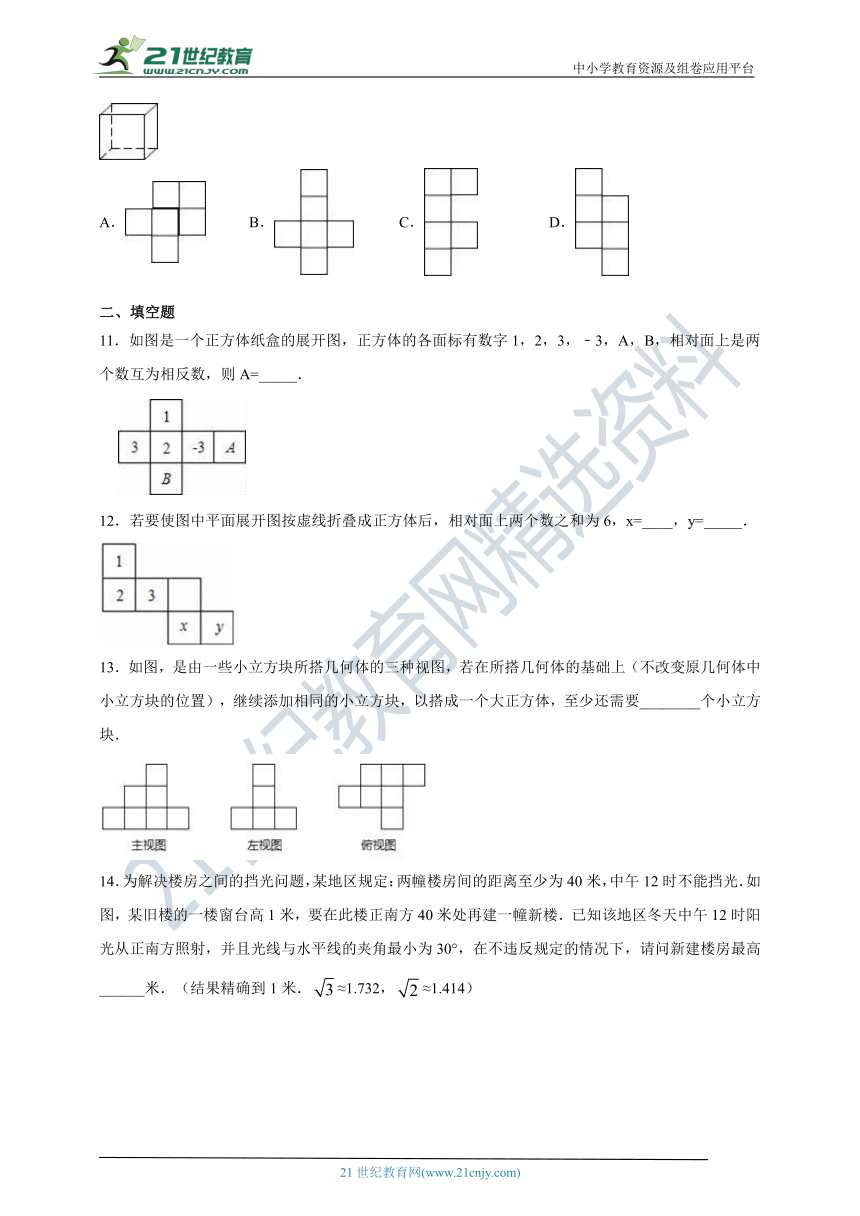
1.如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
A. B. C. D.
2.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
A.13cm B.2cm C. cm D.2cm
3.如图,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )
A. B. C. D.
4.如图所示的几何体是由4个相同的小正方体组成.其主视图为(? )
B. C. D.
5.如图是一个由4个相同的长方体组成的立体图形,它的主视图是( )
A. B. C. D.
6.将一个正方体沿某些棱展开后,能够得到的平面图形是( )
A. B. C. D.
7.如图,是一个用若干个相同的小立方块搭成的几何体的三视图,则组成这个几何体的小立方块的个数是(?? )
A.2 B.3 C.4 D.5
8.如图,是一个正方体的平面展开图,且相对两个面表示的整式的和都相等,如果 ,则E所代表的整式是(?? )
A. B. C. D.
9.若一个几何体的三视图如图所示,则这个几何体是( )
A.三棱柱 B.四棱柱 C.五棱柱 D.长方体
10.如图是一个正方体,则它的表面展开图可以是( )
A. B. C. D.
二、填空题
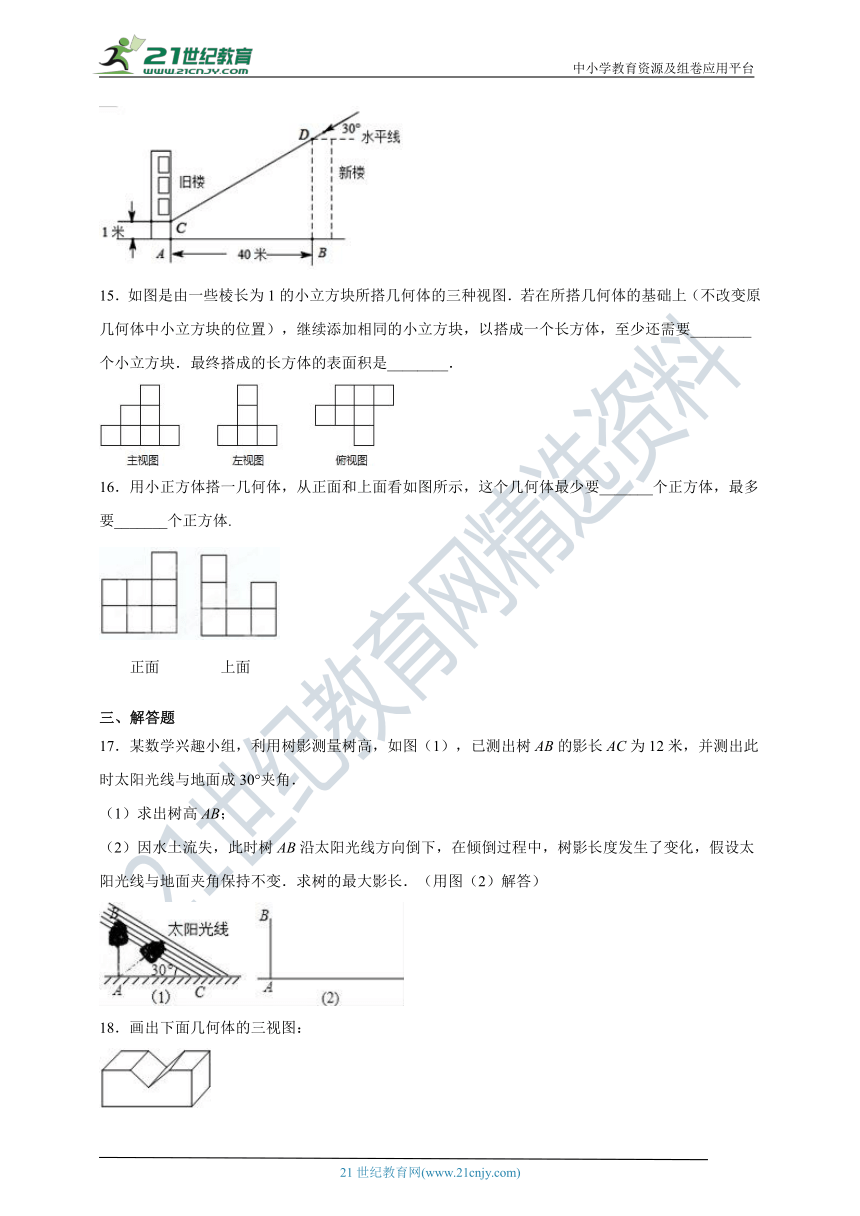
11.如图是一个正方体纸盒的展开图,正方体的各面标有数字1,2,3,﹣3,A,B,相对面上是两个数互为相反数,则A=_____.
12.若要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和为6,x=____,y=_____.
13.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块.
14.为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高______米.(结果精确到1米.≈1.732,≈1.414)
15.如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要________个小立方块.最终搭成的长方体的表面积是________.
16.用小正方体搭一几何体,从正面和上面看如图所示,这个几何体最少要_______个正方体,最多要_______个正方体.
正面 上面
三、解答题
17.某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
18.画出下面几何体的三视图:
19.如图是两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸单位(毫米),求这个几何体的表面积.
20.按要求完成问题:(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二),请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三),它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
21.如图,粗线表示嵌在玻璃正方体内的一根铁丝,请画出该正方体的三视图.
22.一个正方体的五个面的展开情况如图所示,请你在图中的适当位置补出第六个面来.(要求画出2种不同的情况)
23.小明和小彬观察同一个物体,从俯视图看都是一个等腰梯形,但小明所看到的主视图如图(1)所示,小彬看到的主视图如图(2)所示.你知道这是一个什么样的物体?小明和小彬分别是从哪个方向观察它的?
24.综合与实践:制作无盖盒子
任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4cm,容积为616cm3的无盖长方体盒子(纸板厚度忽略不计).
(1)请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
(2)请求出这块矩形纸板的长和宽.
任务二:图2是一个高为4cm的无盖的五棱柱盒子(直棱柱),图3是其底面,在五边形ABCDE中,BC=12cm,AB=DC=6cm,∠ABC=∠BCD=120°,∠EAB=∠EDC=90°.
(1)试判断图3中AE与DE的数量关系,并加以证明.
(2)图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果(图中实线表示剪切线,虚线表示折痕.纸板厚度及剪切接缝处损耗忽略不计).
参考答案
1.B【解析】从左面看易得第一层有2个正方形,第二层最左边有一个正方形.故选B.
2.A【解析】如图:
∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,
此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,
∴A′D=5cm,BD=12-3+AE=12cm,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B=(cm).故选A.
3.B【解析】观察由几何体可得主视图和俯视图分别为,故答案选B.
4.D【解析】从正面看得到2列正方形的个数依次为2,1,故选D.
【点睛】
此题主要考查了几何体的三视图;掌握主视图是从几何体正面看得到的平面图形是解决本题的关键.
5.A【解析】由三视图的定义可知,A是该几何体的三视图,B、C、D不是该几何体的三视图.
故选A.
6.C【解析】由四棱柱四个侧面和上下两个底面的特征可知,
A、B、上底面不可能有两个,故不是正方体的展开图;
D、出现了田字格,故不能;
C、可以拼成一个正方体.故选C.
7.C【解析】综合三视图可知,这个几何体的底层应该有3个小正方体,
第二层有1个小正方体,因此搭成这个几何体所用小正方体的个数是3+1=4个.
故选C.
8.B【解析】由图可得:面A和面E相对,面B和面D,相对面C和面F相对.由题意得:A+E=B+D,代入可得:a3+a2b+3+E=a2b﹣3+[﹣(a2b﹣6)],解得:E=-a3﹣a2b-3.故选B.
9.A
【解析】根据图中三视图的形状,符合条件的只有直三棱柱,因此这个几何体的名称是直三棱柱.
故选A.
10.B【解析】根据含有田字形和凹字形的图形不能折成正方体可判断A、C,D,故此可得到答案.
A、含有田字形,不能折成正方体,故A错误;B、能折成正方体,故B正确;C、凹字形,不能折成正方体,故C错误;D、含有田字形,不能折成正方体,故D错误
11.﹣2【解析】由图可知A=-2.
12.5, 3
【解析】这是一个正方体的平面展开图,共有六个面,其中面“1”与面“x”相对,面“3”与面“y”相对,
则1+x=6,3+y=6,解得:x=5,y=3.故答案是:5,3.
13.54
【解析】由主视图可知,搭成的几何体有三层,且有4列;由左视图可知,搭成的几何体共有3行;
第一层有7个正方体,第二层有2个正方体,第三层有1个正方体,
共有10个正方体,∵搭在这个几何体的基础上添加相同大小的小正方体,以搭成一个大正方体,
∴搭成的大正方体的共有4×4×4=64个小正方体,∴至少还需要64-10=54个小正方体.
14.24
【解析】如图,过点C作CE⊥BD与点E.
在Rt△CDE中,∠DCE=30°,CE=AB=40,则DE=tan30°?CE40≈23,而EB=AC=1,∴BD=DE+EB=231=24(米).
15.26 66
【解析】由俯视图易得最底层有7个小立方体,第二层有2个小立方体,第三层有1个小立方体,其小正方块分布情况如下:
那么共有7+2+1=10个几何体组成.
若搭成一个大长方体,共需3×4×3=36个小立方体,所以还需36-10=26个小立方体,
最终搭成的长方体的表面积是3×4×2+3×3×2+3×4×2=66,故答案为:26,66.
16.10 14 【解析】搭这样的几何体最少需要7+2+1=10个小正方体,
最多需要7+4+3=14个小正方体;
故最多需要14个小正方体,最少需要10个小正方体.故答案为:10,14;
17.(1)树AB的高约为4m;(2)8m.
【解析】(1)AB=ACtan30°=12×=(米).答:树高约为米.
(2)如图(2),B1N=AN=AB1sin45°=×=(米).
NC1=NB1tan60°=×=(米).
AC1=AN+NC1=+.
当树与地面成60°角时影长最大AC2(或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大)
AC2=2AB2=;
(1)在直角△ABC中,已知∠ACB=30°,AC=12米.利用三角函数即可求得AB的长;
(2)在△AB1C1中,已知AB1的长,即AB的长,∠B1AC1=45°,∠B1C1A=30°.过B1作AC1的垂线,在直角△AB1N中根据三角函数求得AN,BN;再在直角△B1NC1中,根据三角函数求得NC1的长,再根据当树与地面成60°角时影长最大,根据三角函数即可求解.
18.【解析】主视图为:;
俯视图为:;左视图.
19.这个几何体的表面积是376mm2
【解析】根据三视图可得:上面的长方体长6mm,高6mm,宽3mm,
下面的长方体长8mm,宽10mm,高3mm,
2(3×8+3×10+8×10)+2×(3×6+6×6)=268+108=376mm2.
答:这个几何体的表面积是376mm2.
20.(1)如图(一),左视图没有发生改变;(2)如图1所示见解析,(3)如图2所示见解析.
【解析】(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,
新几何体的三视图与原几何体的三视图相比,左视图没有发生改变;
(2)如图1所示,(3)如图2所示.
21.见解析.
【解析】如图所示.
22.见解析(答案部唯一).
【解析】如图:
23【解析】底面为等腰梯形的四棱柱(如图所示).小明是从前面观察的,而小彬则是从后面观察的(答案不惟一).
24.任务一:(1)作图见试题解析;(2)30,15;任务二(1)AE=DE;(2),.
【解析】任务一:(1)如图1所示:
(2)设矩形纸板的宽为xcm,则长为2xcm,由题意得:4(x﹣2×4)(2x﹣2×4)=616,解得:,(舍去),∴2x=2×15=30,
答:矩形纸板的长为30cm,宽为15cm;
任务二:(1)AE=DE,证明如下:延长EA,ED分别交直线BC于M,N,∵∠ABC=∠BCD=120°,∴∠ABM=∠DCN=60°,∵∠EAB=∠EDC=90°,∴∠M=∠N=30°,∴EM=EN,在△MAB与△NDC中,∵∠M=∠N,∠ABM=∠DCN,AB=DC,∴△MAB≌△NDC,∴AM=DN,∴EM﹣AM=EN﹣DN,∴AE=DE;
(2)如图4,由(1)得;AE=DE,∠EAD=∠EDA=30°,由已知得,AG=DF=4,连接AD,GF,过B,C分别作BM⊥AD于M,CN⊥AD于N,过E作EP⊥AD于P,则GF即为矩形纸板的长,MN=BC=12,AP=DP,∴∠BAM=∠CDN=60°,∵AB=CD=6,∴AM=DN=3,BM=CN=,∴AP=AD=(3+3+12)=9,∴AE=,PE=,∵AD∥GF,∴△EAD∽△EGF,∴,∴GF=,∴矩形纸板的长至少为,矩形纸板的宽至少为PE+BM++4==.
试卷第1页,总3页
试卷第1页,总3页
