第四章 平行四边形单元测试卷A（含解析）

平行四边形单元测试卷（A）
一、单选题
1．□ABCD中，E、F是对角线BD上不同的两点，下列条件中，不能得出四边形AECF一定为平行四边形的是（ ）
A．BE=DF B．AE=CF C．AF//CE D．∠BAE=∠DCF
2．从六边形的一个顶点出发，可以画出m条对角线，它们将六边形分成n个三角形．则m，n的值分别为 ( )
A．4，3 B．3，3 C．3，4 D．4，4
3．若正多边形的一个外角是40°，则这个正多边形是（　　）
A．正七边形 B．正八边形 C．正九边形 D．正十边形
4．我国传统文化中的“福禄寿喜”图（如图）由四个图案构成．这四个图案中既是轴对称图形，又是中心对称图形的是（　　）
A． B． C． D．
5．根据如图所示的三个图所表示的规律，依次下去第n个图中平行四边形的个数是（?? ）

A．3n??? B．3n（n+1）?? C．6n?? D．6n（n+1）
6．一个正n边形的每一个外角都是36°，则n=（　　）
A．7 B．8 C．9 D．10
7．将一矩形纸片沿一条直线剪成两个多边形，那么这两个多边形的内角和之和不可能是（　　）
A．360° B．540° C．720° D．900°
8．若一个多边形内角和等于1260°，则该多边形边数是( )
A．8 B．9 C．10 D．11
9．七边形外角和为( )
A．180° B．360° C．900° D．1 260°
10．正n边形的内角和等于900°，则n的值为（　　）
A．5 B．6 C．7 D．8



二、填空题
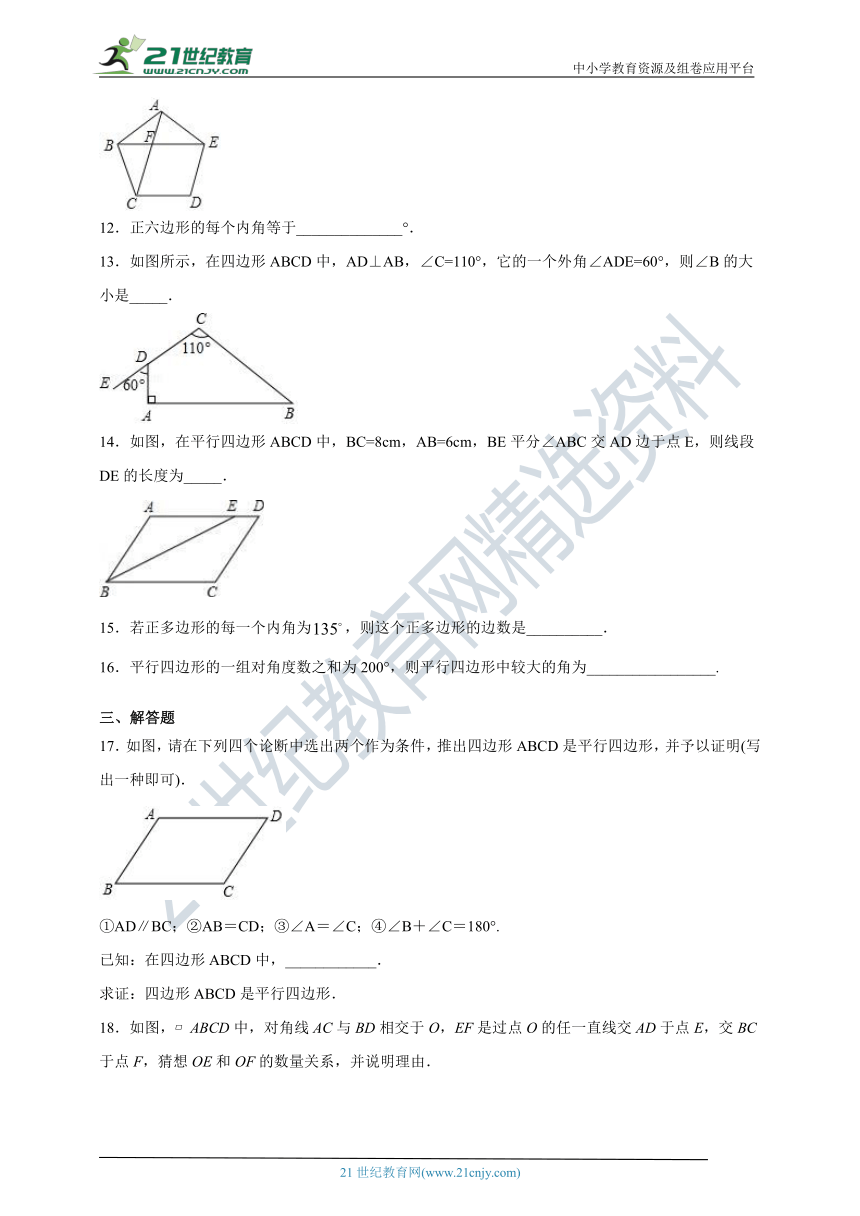
11．如图，在正五边形ABCDE中，AC与BE相交于点F，则∠AFE的度数为_____．

12．正六边形的每个内角等于______________°．
13．如图所示，在四边形ABCD中，AD⊥AB，∠C=110°，它的一个外角∠ADE=60°，则∠B的大小是_____．

14．如图，在平行四边形ABCD中，BC=8cm，AB=6cm，BE平分∠ABC交AD边于点E，则线段DE的长度为_____．

15．若正多边形的每一个内角为，则这个正多边形的边数是__________．
16．平行四边形的一组对角度数之和为200°，则平行四边形中较大的角为_________________.

三、解答题
17．如图，请在下列四个论断中选出两个作为条件，推出四边形ABCD是平行四边形，并予以证明(写出一种即可)．

①AD∥BC；②AB＝CD；③∠A＝∠C；④∠B＋∠C＝180°.
已知：在四边形ABCD中，____________．
求证：四边形ABCD是平行四边形．


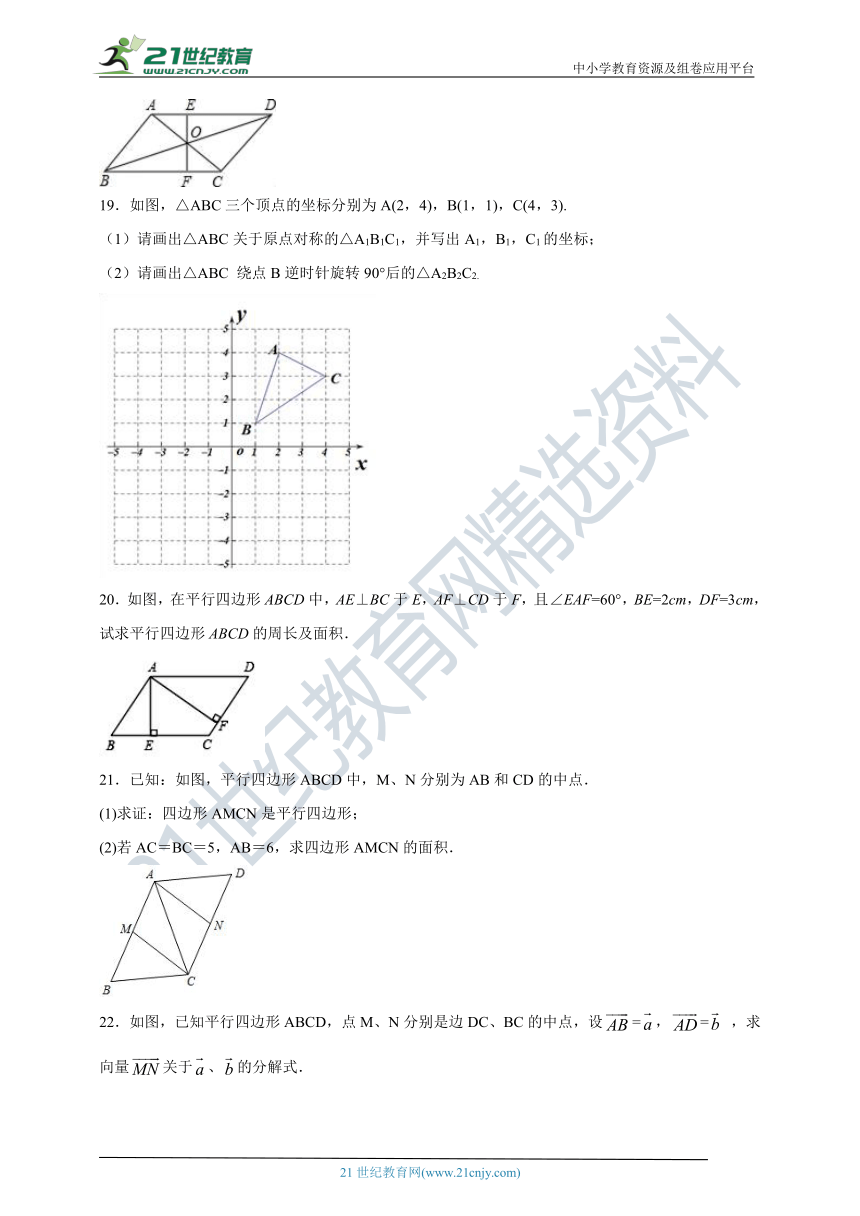
18．如图，?ABCD中，对角线AC与BD相交于O，EF是过点O的任一直线交AD于点E，交BC于点F，猜想OE和OF的数量关系，并说明理由．

19．如图，△ABC三个顶点的坐标分别为A(2，4)，B(1，1)，C(4，3).
（1）请画出△ABC关于原点对称的△A1B1C1，并写出A1，B1，C1的坐标；
（2）请画出△ABC 绕点B逆时针旋转90°后的△A2B2C2.

20．如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，且∠EAF=60°，BE=2cm，DF=3cm，试求平行四边形ABCD的周长及面积．

21．已知：如图，平行四边形ABCD中，M、N分别为AB和CD的中点．
(1)求证：四边形AMCN是平行四边形；
(2)若AC＝BC＝5，AB＝6，求四边形AMCN的面积．

22．如图，已知平行四边形ABCD，点M、N分别是边DC、BC的中点，设=，= ，求向量关于、的分解式．

23．如图，E、F分别为?ABCD的边BC、AD上的点，且∠1＝∠2．求证：四边形AECF是平行四边形．

24．如图，在平面直角坐标系中，已知点，轴于A．
画出将绕原点顺时针旋转后所得的，并写出点、的坐标；
画出关于原点O的中心对称图形，并写出点、的坐标．




参考答案
1．B【解析】A、如图，∵四边形ABCD是平行四边形，∴OA=OC，OB=OD，
∵BE=DF，∴OE=OF，∴四边形AECF是平行四边形，故不符合题意；

B、如图所示，AE=CF，不能得到四边形AECF是平行四边形，故符合题意；

C、如图，∵四边形ABCD是平行四边形，∴OA=OC，
∵AF//CE，∴∠FAO=∠ECO，
又∵∠AOF=∠COE，∴△AOF≌△COE，∴AF=CE，
∴AF CE，∴四边形AECF是平行四边形，故不符合题意；

D、如图，∵四边形ABCD是平行四边形，∴AB=CD，AB//CD，
∴∠ABE=∠CDF，
又∵∠BAE=∠DCF，∴△ABE≌△CDF，∴AE=CF，∠AEB=∠CFD，∴∠AEO=∠CFO，
∴AE//CF，
∴AE CF，∴四边形AECF是平行四边形，故不符合题意，
故选B.


2．C【解析】对角线的数量=6﹣3=3条；
分成的三角形的数量为n﹣2=4个．故选C．
3．C【解析】多边形的外角和是360°，已知该多边形是正多边形，所以每个外角的度数是一样的，即可得这个多边形的边数就是360°÷40°=9.故选C.
4．B【解析】
A、不是轴对称图形，也不是中心对称图形．故错误；
B、是轴对称图形，也是中心对称图形．故正确；
C、是轴对称图形，不是中心对称图形．故错误；
D、不是轴对称图形，也不是中心对称图形．故错误．故选B．
5．B【解析】从图中我们发现
(1)中有6个平行四边形，
(2)中有18个平行四边形,
(3)中有36个平行四边形,
∴第n个中有3n(n+1)个平行四边形.故选B.
6．D【解析】∵一个正n边形的每一个外角都是36°，
∴n=360°÷36°=10，故选D．
7．D【解析】①将矩形沿对角线剪开，得到两个三角形，两个多边形的内角和：180°+180°=360°；
②将矩形从一顶点剪向对边，得到一个三角形和一个四边形，两个多边形的内角和为：180°+360°=540°；
③将矩形沿一组对边剪开，得到两个四边形，两个多边形的内角和为：180°+540°=720°，
④将矩形沿一组邻边剪开，得到一个三角形和一个五边形，其内角和为：180°+540°=720°，故选D.
8．B【解析】∵一个多边形内角和等于1260°，
∴(n?2)×180°=1260°，
解得，n=9.故选B.
9．B【解析】∵任意多边形的外角和为360°，
∴七边形的外角和为360°，故选B．
10．C
【解析】这个多边形的边数是n，
则：（n﹣2）180°=900°，解得n=7．故选：C．
11．72°【解析】∵五边形ABCDE为正五边形，
∴AB=BC=AE，∠ABC=∠BAE=108°，
∴∠BAC=∠BCA=∠ABE=∠AEB=（180°?108°）÷2=36°，
∴∠AFE=∠BAC+∠ABE=72°，
故答案为72°．
12．120【解析】六边形的内角和为：（6-2）×180°=720°，
∴正六边形的每个内角为：=120°.
13．40°【解析】∵∠ADE=60°，
∴∠ADC=120°，∵AD⊥AB，
∴∠DAB=90°，∴∠B=360°﹣∠C﹣∠ADC﹣∠A=40°，故答案为40°．
14．2cm．
【解析】∵四边形ABCD为平行四边形，
∴AE∥BC，AD=BC=8cm，∴∠AEB=∠EBC，
∵BE平分∠ABC，∴∠ABE=∠EBC，∴∠ABE=∠AEB，
∴AB=AE=6cm，∴DE=AD﹣AE=8﹣6=2（cm）.
15．八（或8）
【解析】根据正多边形的每一个内角为，
正多边形的每一个外角为：
多边形的边数为： 故答案为八.
16．100°
【解析】根据平行四边形的性质：对角相等，邻角互补来解答．一组对角的度数之和为200°，则该组对角均为100°．又因为平行四边形邻角互补，所以，另一组对角均为180°－100°＝80°．所以，较大的角为100°．故答案：100°.
17．已知：①③（或①④或②④或③④），证明见解析．
【解析】已知：①③，①④，②④，③④均可，其余均不可以．
已知：在四边形ABCD中，①AD∥BC，③∠A=∠C，
求证：四边形ABCD是平行四边形．
证明：∵AD∥BC，
∴∠A+∠B=180°，∠C+∠D=180°．
∵∠A=∠C，
∴∠B=∠D．
∴四边形ABCD是平行四边形．

18．结论：OE=OF．理由见解析.
【解析】结论：OE=OF．
理由∵四边形ABCD是平行四边形，
∴OA=OC，AD∥BC，
∴∠OAE=∠OCF，
在△AOE和△COF中，
，
∴△AOE≌△COF，
∴OE=OF．

19．答案见解析.
【解析】（1）如下图：△A1B1C1为所求三角形，A1的坐标为（-2，-4）、B1的坐标为（-1，-1）、C1的坐标为（-4，-3）；

（2）如下图：△A2B2C2为所求三角形.

20．20cm,cm2
【解析】∵AE⊥BC，AF⊥CD，∠EAF=60°，∴∠AEB=∠AEC=∠AFC=∠AFD=90°，∴∠C=120°．
∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，AD∥BC，∠B=∠D，∴∠B+∠C=180°，∴∠B=∠D=60°，∴∠BAE=∠FAD=30°．
∵BE=2cm，FD=3cm，∴AB=4cm，BC=AD=6cm，AF=3，∴ABCD周长=2（AB+BC）=2（4+6）=20 cm，S?ABCD=CD?AF=4×3=12cm2．
21．（1）见解析；（2）12.
【解析】（1）∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∵M，N分别为AB和CD的中点，
∴AM=AB，CN=CD，
∴AM=CN，且AB∥CD，
∴四边形AMCN是平行四边形；
（2）∵AC=BC=5，AB=6，M是AB中点，
∴AM=MB=3，CM⊥AM，
∴CM=，
∵四边形AMCN是平行四边形，且CM⊥SM，
∴AMCN是矩形，
∴S四边形AMCN=12.

22．【解析】连接BD,
∵点M、N分别是边DC、BC的中点，∴MN是△BCD的中位线，
∴MN∥BD，MN= BD，
∵ ，
∴ .
23．【解析】证明：∵四边形ABCD为平行四边形，
∴AD∥BC，
∴∠1=∠EAF，
∵∠1=∠2，
∴∠EAF=∠2，
∴AE∥CF，
∴四边形AECF是平行四边形．
24．(1)见解析，，；（2）见解析，
【解析】如图所示，即为所求，

由图可知，，；
如图所示，即为所求，
由图可知，．












试卷第1页，总3页


试卷第1页，总3页