第四章 平行四边形单元测试卷B（含解析）

平行四边形单元测试卷（B）
一、单选题
1．如图，在四边形ABCD中，AB∥CD，要使得四边形ABCD是平行四边形，可添加的条件不正确的是 ( )

A．AB=CD B．BC∥AD C．BC=AD D．∠A=∠C
2．如图，在平行四边形ABCD中，∠DBC=45°，DE⊥BC于E，BF⊥CD于F，DE，BF相交于H，BF与AD的延长线相交于点G，下面给出四个结论:①； ②∠A=∠BHE； ③AB=BH； ④△BCF≌△DCE， 其中正确的结论是(　　).

A．①②③ B．①②④ C．②③④ D．①②③④
3．如图，点P（3，4），⊙P半径为2，A（2.8，0），B（5.6，0），点M是⊙P上的动点，点C是MB的中点，则AC的最小值是（　　）

A．1.4 B． C． D．2.6
4．如图，P为□ABCD对角线BD上一点，△ABP的面积为S1，△CBP的面积为S2，则S1和S2的关系为 （ ）

S1>S2 B．S1=S2 C．S1
5．已知 ABC(如图1)，按图2所示的尺规作图痕迹不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是（?? ）

A．两组对边分别平行的四边形是平行四边形 B．两组对边分别相等的四边形是平行四边形
C．一组对边平行且相等的四边形是平行四边形 D．对角线互相平分的四边形是平行四边形
6．如图，在□ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上（E不与A、B重合），连接EF、CF，则下列结论中一定成立的是 ( )

①∠DCF=∠BCD；②EF=CF；③；④∠DFE=4∠AEF
A．①②③④ B．①②③ C．①② D．①②④
7．已知?ABCD中，AD=2AB，F是BC的中点，作AE⊥CD，垂足E在线段CD上，连结EF、AF，下列结论：①2∠BAF=∠BAD；②EF=AF；③S△ABF≤S△AEF；④∠BFE=3∠CEF，中一定成立的是（　　）

①②④ B．①③
C．②③④ D．①②③④
8．如图，在平行四边形ABCD中，按下列条件得到的四边形EFGH不一定是平行四边形的是( )
A．B．
C．D．
9．在面积为12的平行四边形ABCD中，过点A作直线BC的垂线交直线BC于点E，过点A作直线CD的垂线交直线CD于点F，若AB=4，BC=6，则CE+CF的值为( )
A． B．
C．或 D．或
10．如图，已知ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC=60°，∠ADA′=45°，则∠DA′E′的大小为（ ）

A．170° B．165° C．160° D．155°

二、填空题
11．如图，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若EF=2，BC=10，则AB的长为___________．

12．如图，在平行四边形ABCD中，对角线AC、BD相交于点O，AB=OB，点E、点F分别是OA、OD的中点，连接EF，∠CEF=45°，EM⊥BC于点M，EM交BD于点N，FN=，则线段BC的长为_____．




13．如图，在ABCD中，点P是AB的中点，PQ∥AC交BC于点Q，连接AQ，CP，则图中与△APC面积相等的三角形有________个．

14．如图，在□ABCD中，E、F分别是AB、DC边上的点，AF与DE交于点P，BF与CE交于点Q，若S△APD=20cm2，S△BQC=30cm2，则图中阴影部分的面积为_____cm2．

15．如图，四边形中，，，，点、分别线段、上的动点，（含端点，但点不与点重合），点、分别为、的中点，则长度的最大值为__________．

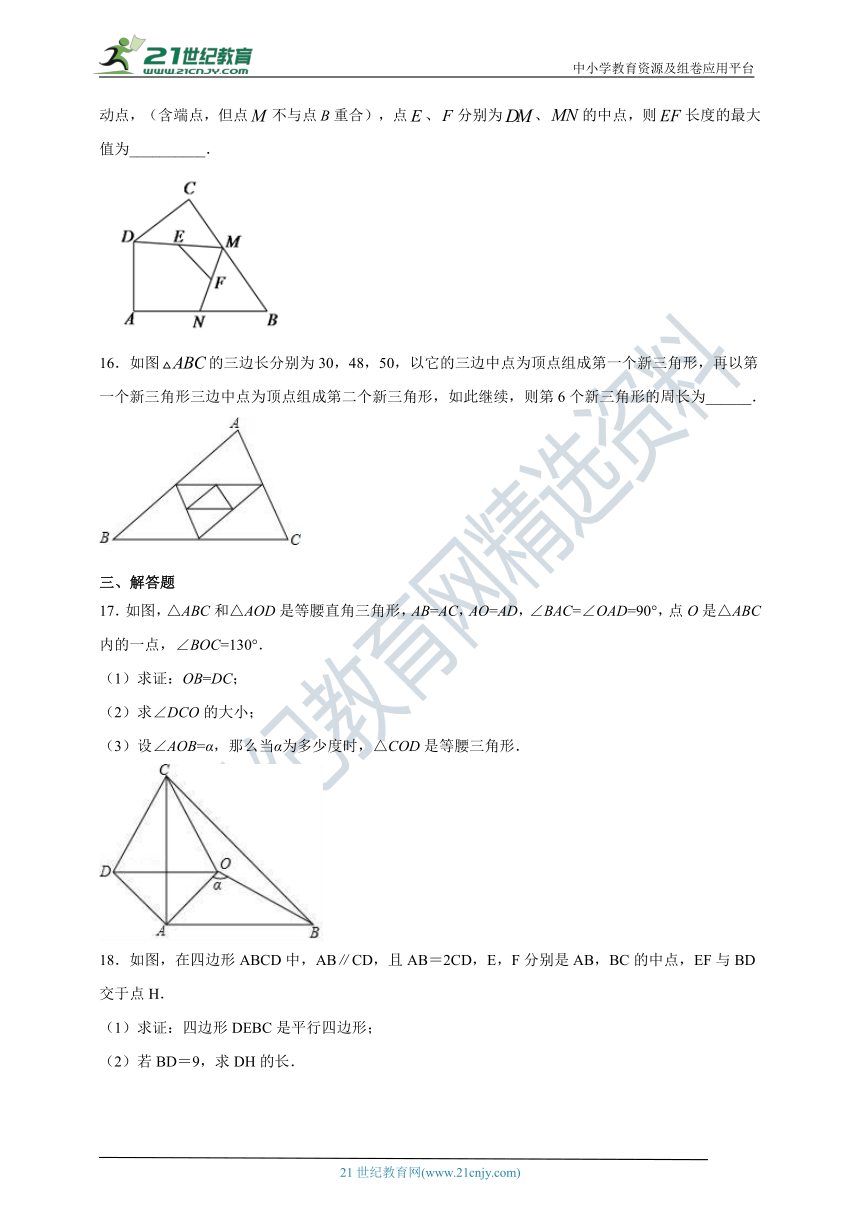
16．如图的三边长分别为30，48，50，以它的三边中点为顶点组成第一个新三角形，再以第一个新三角形三边中点为顶点组成第二个新三角形，如此继续，则第6个新三角形的周长为______．


三、解答题
17．如图，△ABC和△AOD是等腰直角三角形，AB=AC，AO=AD，∠BAC=∠OAD=90°，点O是△ABC内的一点，∠BOC=130°．
（1）求证：OB=DC；
（2）求∠DCO的大小；
（3）设∠AOB=α，那么当α为多少度时，△COD是等腰三角形．

18．如图，在四边形ABCD中，AB∥CD，且AB＝2CD，E，F分别是AB，BC的中点，EF与BD交于点H．
（1）求证：四边形DEBC是平行四边形；
（2）若BD＝9，求DH的长．

19．如图，六边形ABCDEF的内角都相等，CF∥AB．
(1)求∠FCD的度数；
(2)求证：AF∥CD．

20．如图，在平行四边形ABCD中，点E是CD的中点，点F是BC边上的点，AF=AD+FC，平行四边形ABCD的面积为S，由A、E、F三点确定的圆的周长为t．
（1）若△ABE的面积为30，直接写出S的值；
（2）求证：AE平分∠DAF；
（3）若AE=BE，AB=4，AD=5，求t的值．

21．如图，平面直角坐标系中，已知点A(0，5)，点P(m，5)在第二象限，连接AP、OP
(1) 如图1，若OP＝6，求m的值
(2) 如图2，点C在x轴负半轴上，以CP为斜边作直角三角形BCP，∠CBP＝90°，且∠BPC＝∠APO．取OC的中点D，连接AD、BD，求证：AD＝BD
(3) 如图3，将△AOP沿直线OP翻折得到△EOP（点A的对应点为点E）．若点E到x轴的距离不大于3，直接写出m的取值范围（无需解答过程）

22．将△ABC的边AB绕点A顺时针旋转α得到AB′，边AC绕点A逆时针旋转β得到AC′，α＋β=180°．连接B′C′，作△AB′C′的中线AD．
（初步感知）
（1）如图①，当∠BAC=90°，BC＝4时，AD的长为______；
（探索证明）
（2）如图②，△ABC为任意三角形时，猜想AD与BC的数量关系，并证明；
（应用延伸）
（3）如图③，已知等腰△ACB，AC=BC=m，延长AC到D，延长CB到E，使CD=CE=n,将△CED绕C顺时针旋转一周得到△CE′D′，连接BE′、AD′，若∠CBE′=90°，求AD′的长度（用含m、n的代数式表示）．

23．如图，在平面直角坐标系中，已知点A(0，6)，B(b，0)，且b＜0，C，D分别是OA，AB的中点，△AOB的外角∠DBF的平分线BE与CD的延长线交于点E.
(1)求证：∠DAO＝∠DOA；
(2)①若b＝－8，求CE的长；
②若CE＝＋1，则b＝________；
(3)是否存在这样的b值，使得四边形OBED为平行四边形？若存在，请求出此时四边形OBED对角线的交点坐标；若不存在，请说明理由．

24．如图，在平面直角坐标系中，已知点A(0，6)，B(b，0)，且b＜0，点C，D分别是OA，AB的中点，△AOB的外角平分线与CD的延长线交于点E.
(1)求证：∠DAO＝∠DOA；
(2)①若b＝－8，求CE的长；
②若CE＝＋1，则b＝________．
(3)是否存在这样的b值，使得四边形OBED为平行四边形？若存在，请求出此时四边形OBED对角线的交点坐标；若不存在，请说明理由．
(4)直线AE与x轴交于点F，请用含b的式子直接写出点F的坐标．




参考答案
1．C【解析】∵AB∥CD，∴当AB=CD时，由一组对边平行且相等的四边形为平行四边形可知该条件正确； 当BC∥AD时，由两组对边分别平行的四边形为平行四边形可知该条件正确；
当BC=AD时，该四边形可能为等腰梯形，故该条件不正确；当∠A=∠C时，可求得∠B=∠D，由两组对角分别相等的四边形为平行四边形可知该条件正确． 故选C．
2．A【解析】∵∠DBC=45°，DE⊥BC于E，
∴在Rt△DBE中，BE2+DE2=BD2，BE=DE，
∴BD=BE，故①正确；∵DE⊥BC，BF⊥DC，∴∠BHE和∠C都是∠HBE的余角，
∴∠BHE=∠C，又∵在?ABCD中，∠A=∠C，
∴∠A=∠BHE，故②正确；在△BEH和△DEC中，
，∴△BEH≌△DEC，∴BH=CD，
∵四边形ABCD为平行四边形，∴AB=CD，∴AB=BH，故③正确；利用已知条件不能得到△BCF≌△DCE，故④错误，故选A.
3．B【解析】如图，连接OP交⊙P于M′，连接OM，
由勾股定理得：OP==5，
∵OA=AB，CM=CB，∴AC=OM，
∴当OM最小时，AC最小，∴当M运动到M′时，OM最小，
此时AC的最小值=OM′=（OP﹣PM′）=×（5-2）=，

4．B【解析】∵在□ABCD中，点A、C到BD的距离相等，设为h.
∴S1= S△ABP=BP ,S2= S△CPB=BP.
∴S1=S2,故选：B.
5．D【解析】根据作图可知，先作线段AC的垂直平分线MN，交AC于点O

∴OA=OC，
再以O为圆心OB为半径画弧，交射线BO于点D
∴OB=OD
∴四边形ABCD是平行四边形（对角线互相平分的四边形是平行四边形）
6．B【解析】①∵F是AD的中点，∴AF=FD．
∵在?ABCD中，AD=2AB，∴AF=FD=CD，∴∠DFC=∠DCF．
∵AD∥BC，∴∠DFC=∠FCB，∴∠DCF=∠BCF，∴∠DCF=∠BCD，故①正确；
延长EF，交CD延长线于M．∵四边形ABCD是平行四边形，∴AB∥CD，∴∠A=∠MDF．
∵F为AD中点，∴AF=FD．在△AEF和△DFM中，，∴△AEF≌△DMF（ASA），∴FE=MF，∠AEF=∠M． ∵CE⊥AB，∴∠AEC=90°，∴∠AEC=∠ECD=90°．
∵FM=EF，∴EF=CF，故②正确； ③∵EF=FM，∴S△EFC=S△CFM．
∵MC＞BE，∴S△BEC＜2S△EFC 故③正确；
④设∠FEC=x，则∠FCE=x，∴∠DCF=∠DFC=90°﹣x，∴∠EFC=180°﹣2x，∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x．∵∠AEF=90°﹣x，∴∠DFE=3∠AEF，故④错误．
故答案为①②③．

7．D【解析】因为F是BC的中点，所以F=FC，然后根据平行四边形的性质和AD=2AB，可得到BC=2AB=2CD，即BF=FC=AB，再根据“等边对等角”可得∠AFB=∠BAF，然后平行线的性质，可得∠AFB=∠FAB，即可得到2∠BAF=∠BAD，故①正确；

延长EF，交AB的延长线于M，由平行四边形的性质和中点的性质，可证明△MBF≌△ECF（ASA）然后根据全等三角形的性质和垂直的性质证得EF=AF，故②正确；
根据EF=FM可知S△EFC=S△AFM，所以可得S△ABF≤S△AEF，故③正确；
设∠FEA=x,则∠FAE=x，可得∠BAF=∠AFB=90°-x，进而求得∠EFA=180°-2x，则∠EFB=90°-x+180°-2x=270°-3x，再根据∠CFE=90°-x，可得∠BFE=3∠CEF，故④正确.
故选D.
8．A【解析】选项A，由于所给已知条件只有角的关系，三角形边之间没有等量关系，不能证明三角形全等或边之间平行，也就无法证明四边形EFGH是平行四边形；选项B，连接AC，根据三角形中位线定理，易证EF=GH且EF∥GH，即可得四边形EFGH是平行四边形；选项C，利用AD∥BC，AE、BE是角平分线，易证∠ABE=90°，即可得∠HEF=90°，同理可得∠EFH=∠FGH=∠EHG=90°，从而易证四边形EFGH是矩形，继而得四边形EFGH是平行四边形； 选项D，设平行四边形ABCD对角线的交点为O，由于ABCD是平行四边形，那么∠EAO=∠GCO，且∠AOE=∠COG，OA=OC，利用ASA可证△AOE≌△COG，那么OE=OG，同理OH=OF，从而易证四边形EFGH是平行四边形．故选A．
9．C【解析】∵四边形ABCD是平行四边形，∴AB=CD=4，BC=AD=6．
①如图：

∵S?ABCD=BC?AE=CD?AF=12，∴AE=2，AF=3．在Rt△ABE中，BE=．在Rt△ADF中，DF=，∴CE+CF=BC﹣BE+DF﹣CD=；
②如图：

∵S?ABCD=BC?AE=CD?AF=12，∴AE=2，AF=3．在Rt△ABE中，BE=．在Rt△ADF中，DF=，∴CE+CF=BC+BE+DF+CD=．
综上可得：CE+CF的值为或．故选C．
10．B【解析】∵四边形ABCD是平行四边形,


∵AE⊥BC于点E， ∵△BAE顺时针旋转,得到△BA′E′，
故选B.
11．6
【解析】延长AF交BC于M，

∵DE为△ABC的中位线，
∴AD=BD，AE=EC，DE∥BC，∴AF=FM，
∵BF⊥AM，∴BA=BM，∵AF=FM，AE=EC，
∴CM=2EF=4，∴BM=BC?CM=6，∴AB=BM=6.故答案为：6.
12．
【解析】设EF=x，
∵点E、点F分别是OA、OD的中点，∴EF是△OAD的中位线，
∴AD=2x，AD∥EF，∴∠CAD=∠CEF=45°，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC=2x，∴∠ACB=∠CAD=45°，
∵EM⊥BC，∴∠EMC=90°，
∴△EMC是等腰直角三角形，∴∠CEM=45°，连接BE，

∵AB=OB，AE=OE∴BE⊥AO∴∠BEM=45°，
∴BM=EM=MC=x，∴BM=FE，
易得△ENF≌△MNB，∴EN=MN=x，BN=FN=，
Rt△BNM中，由勾股定理得：BN2=BM2+MN2，
∴()2＝x2+(x)2，x=2或-2（舍），
∴BC=2x=4．故答案为4．
13．3【解析】因为点P是AB的中点，PQ∥AC，
所以，Q是BC的中点，所以，S△APC=S△PBC=S△ABQ=S△ACQ=S△ABC
所以，图中与△APC面积相等的三角形有3个．故答案为：3
14．50【解析】连接EF

∵因为四边形ABCD是平行四边形.
∴AB∥CD
∴△ADF与△DEF同底等高，
∴S△ADF=S△DEF
即S△ADF-S△DPF=S△DEF-S△DPF，
即S△APD=S△EPF=20cm2，
同理可得S△BQC=S△EFQ=30cm2，
∴阴影部分的面积为S△EPF+S△EFQ=20+30=50cm2．
故答案为：50
15．2.5
【解析】∵，，
∴，∴最大时，最大，
∵因为与重合时最大，此时，
∴的最大值为．故答案为．
16．2【解析】如图，、F分别为AB、AC的中点，
，同理可得，，
，
即的周长的周长，
第二个三角形的周长是原三角形周长的，
同理可得的周长的周长的周长的周长，
第三个三角形的周长是原三角形周长的，
第六个三角形的周长是原三角形周长的，
原三角形的三边长为30，48，50，
原三角形的周长为128，
第一个新三角形的周长为64，
第六个三角形的周长，
故答案为：2．

17．（1）证明见解析；（2）40°；（3）当α的度数为115°或85°或145°时，△AOD是等腰三角形．
【解析】（1）∵∠BAC=∠OAD=90°，
∴∠BAC﹣∠CAO=∠OAD﹣∠CAO，
∴∠DAC=∠OAB，
在△AOB与△ADC中，
，
∴△AOB≌△ADC，
∴OB=DC；
（2）∵∠BOC=130°，
∴∠BOA+∠AOC=360°﹣130°=230°，
∵△AOB≌△ADC
∠AOB=∠ADC，
∴∠ADC+∠AOC=230°，
又∵△AOD是等腰直角三角形，
∴∠DAO=90°，
∴四边形AOCD中，∠DCO=360°﹣90°﹣230°=40°；
（3）当CD=CO时，
∴∠CDO=∠COD==70°，
∵△AOD是等腰直角三角形，
∴∠ODA=45°，
∴∠CDA=∠CDO+∠ODA=70°+45°=115°，
又∠AOB=∠ADC=α，
∴α=115°；
当OD=CO时，
∴∠DCO=∠CDO=40°，
∴∠CDA=∠CDO+∠ODA=40°+45°=85°，
∴α=85°；
当CD=OD时，
∴∠DCO=∠DOC=40°，
∠CDO=180°﹣∠DCO﹣∠DOC=180°﹣40°﹣40°=100°，
∴∠CDA=∠CDO+∠ODA=100°+45°=145°，
∴α=145°，综上所述：当α的度数为115°或85°或145°时，△AOD是等腰三角形．
18．（1）证明见解析；（2）6.
【解析】（1）证明：∵E是AB的中点，
∴AB＝2EB，
∵AB＝2CD，
∴DC＝BE，
又∵AB∥CD，即DC∥BE，
∴四边形BCDE是平行四边形．
（2）解：∵四边形BCDE是平行四边形，
∴BC＝DE，BC∥DE，
∴△EDM∽△FBM，
∴＝，
∵BC＝DE，F为BC的中点，
∴BF＝BC＝DE，
∴＝＝2，
∴DH＝2HB，
又∵DH+HB＝9，
∴DH＝6．
19．（1）60°（2）证明见解析
【解析】∵六边形ABCDEF的内角相等，∴∠B＝∠A＝∠BCD＝120°.
∵CF∥AB，∴∠B＋∠BCF＝180°，∴∠BCF＝60°，∴∠FCD＝60°.
(2)证明：∵CF∥AB，∴∠A＋∠AFC＝180°，∴∠AFC＝180°－120°＝60°，∴∠AFC＝∠FCD，∴AF∥CD.
20．（1）平行四边形ABCD的面积为60；（2）证明见解析；（3）△AEF的外接圆的周长t=π．
【解析】（1）如图，作EG⊥AB于点G，
则S△ABE=×AB×EG=30，则AB?EG=60，
∴平行四边形ABCD的面积为60；
（2）如图，延长AE交BC延长线于点H，

∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠ADE=∠HCE，∠DAE=∠CHE，
∵E为CD的中点，
∴CE=ED，
∴△ADE≌△HCE，
∴AD=HC、AE=HE，
∴AD+FC=HC+FC，
由AF=AD+FC和FH=HC+FC得AF=FH，
∴∠FAE=∠CHE，
又∵∠DAE=∠CHE，
∴∠DAE=∠FAE，
∴AE平分∠DAF；
（3）连接EF，
∵AE=BE、AE=HE，
∴AE=BE=HE，
∴∠BAE=∠ABE，∠HBE=∠BHE，
∵∠DAE=∠CHE，
∴∠BAE+∠DAE=∠ABE+∠HBE，即∠DAB=∠CBA，
由四边形ABCD是平行四边形得∠DAB+∠CBA=180°，
∴∠CBA=90°，
∴AF2=AB2+BF2=16+（5﹣FC）2=（FC+CH）2=（FC+5）2，
解得：FC=，
∴AF=FC+CH=，
∵AE=HE、AF=FH，
∴FE⊥AH，
∴AF是△AEF的外接圆直径，
∴△AEF的外接圆的周长t=π．
【点睛】本题考查圆的综合问题，涉及到平行四边形的性质、矩形的判定与性质、全等三角形的判定与性质、等腰三角形的性质、勾股定理等知识，熟练掌握和灵活运用相关的性质与定理是解题的关键.
21．（1）- （2）证明见解析（3）-10≤m≤-
【解析】（1）由点A（0，5），点P（m，5）可知PA⊥y轴，
∵OP=6，OA=5，由勾股定理可求PA=，∴m=-；
（2）如图2，取CP、OP中点M、N，连接DM、DN、BM、AN，

∵D、M、N分别为OC、PC、PO的中点，
∴DM∥PO，DN∥PC，
∴四边形PMDN是平行四边形，
∴PM=DN，DM=PN，∠PMD=∠PND，
又M、N分别为Rt△PBC、Rt△PAO斜边的中点，
∴BM=MP，AN=PN，
∵∠BPC=∠APO
∴∠BMP=∠ANP，
∴∠BMP+∠PMD=∠ANP+∠PND，
∴∠DNA=∠BMD，
∴△DNA≌△BMD，
∴AD=BD；
（3）由条件可知点E的纵坐标大于或等于-3小于或等于3，
①当点E的纵坐标为3时，如图4，过点E作ES⊥x轴于S，交直线AP于R，

在Rt△OES中，OE=OA=5，ES=3，可求OS=AR=4，RE=2，
∵PA=PE=-m，PR=4+m，
在Rt△PRE中，由22+（4+m）2=（-m）2，
解得：m=；
②当点E的纵坐标为-3时，如图5，过点E作ES⊥x轴于S，交直线AP于R，

在Rt△OES中，OE=OA=5，ES=3，
∴OS=AR=4，
∴PR=10-4=6，
由勾股定理得：RE==8，
∵PA=PE=-m，PR=-4-m，
在Rt△△PRE中，由82+（4+m）2=（-m）2，
解得：m=-10，综上所述，当-10≤m≤时，点E到x轴的距离不大于3.
22．（1）2；（2）（2）AD=BC，理由见解析；（3）AD′=.
【解析】（1）∵∠BAC=90°，∠BAC+∠B′AC′=180°，
∴∠B′AC′=∠BAC=90°，
∵AB=AB′，AC=AC′，
∴△BAC≌△B′AC′，
∴BC=B′C′，
∵B′D=DC′，
∴AD=B′C′=BC==2，
故答案为：2；
（2）AD=BC，理由如下：
如图，延长AD至点E，使得DE=AD，

∵B′D=C′D，∴四边形AC′EB′为平行四边形，
∴B′E∥AC′，B′E=AC′=AC，∴∠AB′E＋∠B′AC′=180°，
∵α＋β=180°，∴∠BAC＋∠B′AC′=180°，∴∠AB′E=∠BAC，
∵AB′=AB，∴△AB′E≌△BAC，∴AE=BC，
∴AD=AE=BC；
（3）情况一：如图，过点C作△BCE′的中线CF，

在Rt△BCE′中，由勾股定理
得：；
∴BF=BE′=，
在Rt△BCF中，由勾股定理得：CF===，
由（2）可知：AD′=；
情况二：如图，作△CBE′的中线CF并延长到G，使FG=CF，连接BG、E′G，

∵BF=E′F，CF=GF，∴四边形BCE′G为平行四边形，
∴BC=GE′，BC∥GE′，∵BC=AC，∴AC=GE′，
由旋转可知∠1=∠BCE′，∵∠1+∠ACD′=180°，∠GE′C+∠BCE′=180°，∴∠ACD′=∠GE′C，
∵CD′=E′C，∴△ACD′≌△GE′C，∴AD′=GC
由情况一可知：BE′=，AD′=．
23．(1)见解析；(2) ①9；②－2；(3)见解析.
【解析】(1)∵C，D分别为AO，AB的中点，∴CD∥OB．
又∵OB⊥AO，∴CD⊥AC，∴CD垂直平分AO，∴AD＝OD，∴∠DAO＝∠DOA．
(2)①∵b＝－8，∴OB＝8，∴CD＝OB＝4．易得∠DEB＝∠DBE，∴ED＝BD＝AB＝＝5，∴CE＝CD＋ED＝4＋5＝9．
②由①得：EC=ED+DC=AB+BO，∴，解得：b=－2．故答案为：－2．
(3)存在．理由如下：
如图，∵四边形OBED是平行四边形，∴OB＝ED．
∵ED＝BD＝AB，∴OB＝AB．
∵OB＝－b，∴AB＝－2b，∴(－b)2＋62＝(－2b)2，解得：b＝，∴AB＝．设平行四边形OBED的对角线交点为M，作MH⊥OB于点H，则BM＝BD＝AB＝×＝．
∵OD＝AD，∴OD＝DB＝OB，∴∠DBO＝60°，∴∠BMH＝30°，∴BH＝，MH＝，∴OH＝=，∴M（，）．

24．(1)见解析;(2) ①9, ②－2;(3)见解析;(4) F(b－，0)．
【解析】(1)∵C，D分别为AO，AB的中点，∴CD∥OB．
又∵OB⊥AO，∴CD⊥AC，∴CD垂直平分AO，∴AD＝OD，∴∠DAO＝∠DOA．
(2)①∵b＝－8，∴OB＝8，∴CD＝OB＝4．易得∠DEB＝∠DBE，∴ED＝BD＝AB＝＝5，∴CE＝CD＋ED＝4＋5＝9．
②由①得：EC=ED+DC=AB+BO，∴，解得：b=－2．故答案为：－2．
(3)存在．理由如下：
如图，∵四边形OBED是平行四边形，∴OB＝ED．
∵ED＝BD＝AB，∴OB＝AB．
∵OB＝－b，∴AB＝－2b，∴(－b)2＋62＝(－2b)2，解得：b＝，∴AB＝．设平行四边形OBED的对角线交点为M，作MH⊥OB于点H，则BM＝BD＝AB＝×＝．∵OD＝AD，∴OD＝DB＝OB，∴∠DBO＝60°，∴∠BMH＝30°，∴BH＝，MH＝，∴OH＝=，∴M（，）．

(4) ∵EC∥FO，AC=CO，∴FO=2EC．
∵EC=，∴FO=，∴F(，0)．














试卷第1页，总3页


试卷第1页，总3页