第五章 特殊平行四边形单元测试卷B(含解析)
文档属性
| 名称 | 第五章 特殊平行四边形单元测试卷B(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 00:00:00 | ||
图片预览



文档简介
特殊平行四边形单元测试卷(B)
一、单选题
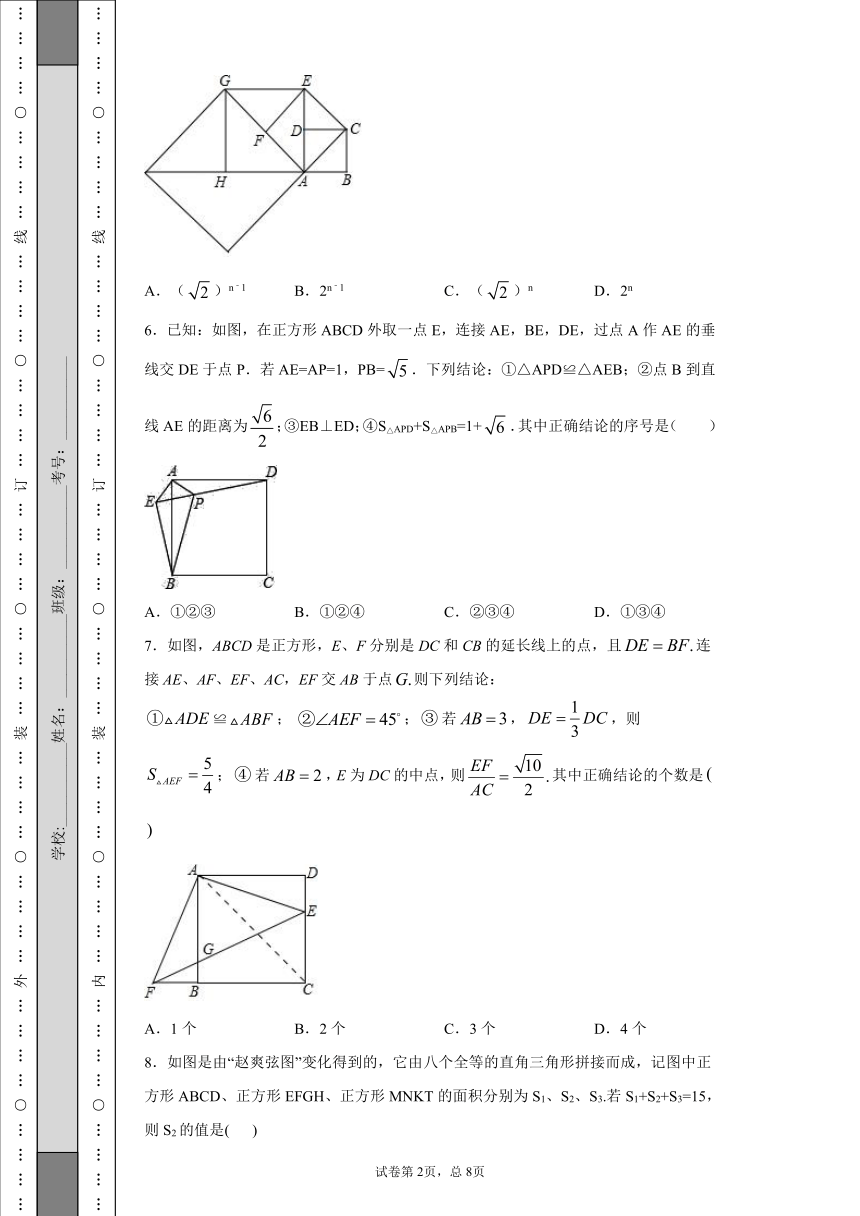
1.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+.其中正确的个数为( )
A.1 B.2 C.3 D.4
2.如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②∠EAG=45°;③CE=2DE;④AG∥CF;⑤S△FGC=.其中正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
3.如图,由两个长为,宽为的全等矩形叠合而得到四边形,则四边形面积的最大值是( )
A.15 B.16 C.19 D.20
4.在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为( )
A.3 B.5 C.3或5 D.3或6
5.如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,依此下去,第n个正方形的面积为( )
A.()n﹣1 B.2n﹣1 C.()n D.2n
6.已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+.其中正确结论的序号是( )
A.①②③ B.①②④ C.②③④ D.①③④
7.如图,ABCD是正方形,E、F分别是DC和CB的延长线上的点,且连接AE、AF、EF、AC,EF交AB于点则下列结论:≌;?;若,,则;?若,E为DC的中点,则其中正确结论的个数是
A.1个 B.2个 C.3?个 D.4?个
8.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=15,则S2的值是(???? )
A.3 B. C.5 D.
9.如图,平行四边形 ABCD 中,AD∥BC,AB=BC=CD=AD=4,∠A=∠C=60°,连接 BD,将△BCD 绕点 B 旋转,当 BD(即 BD′)与 AD 交于一点 E,BC(即 BC′)同时与 CD 交于一点 F 时,下列结论正确的是( )
①AE=DF;②∠BEF=60°;③∠DEB=∠DFB;④△DEF 的周长的最小值是4+2
A.①② B.②③ C.①②④ D.①②③④
10.如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2018次相遇在边 ( )上.
A.AB B.BC C.CD D.DA
二、填空题
11.折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在线段AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=_____.
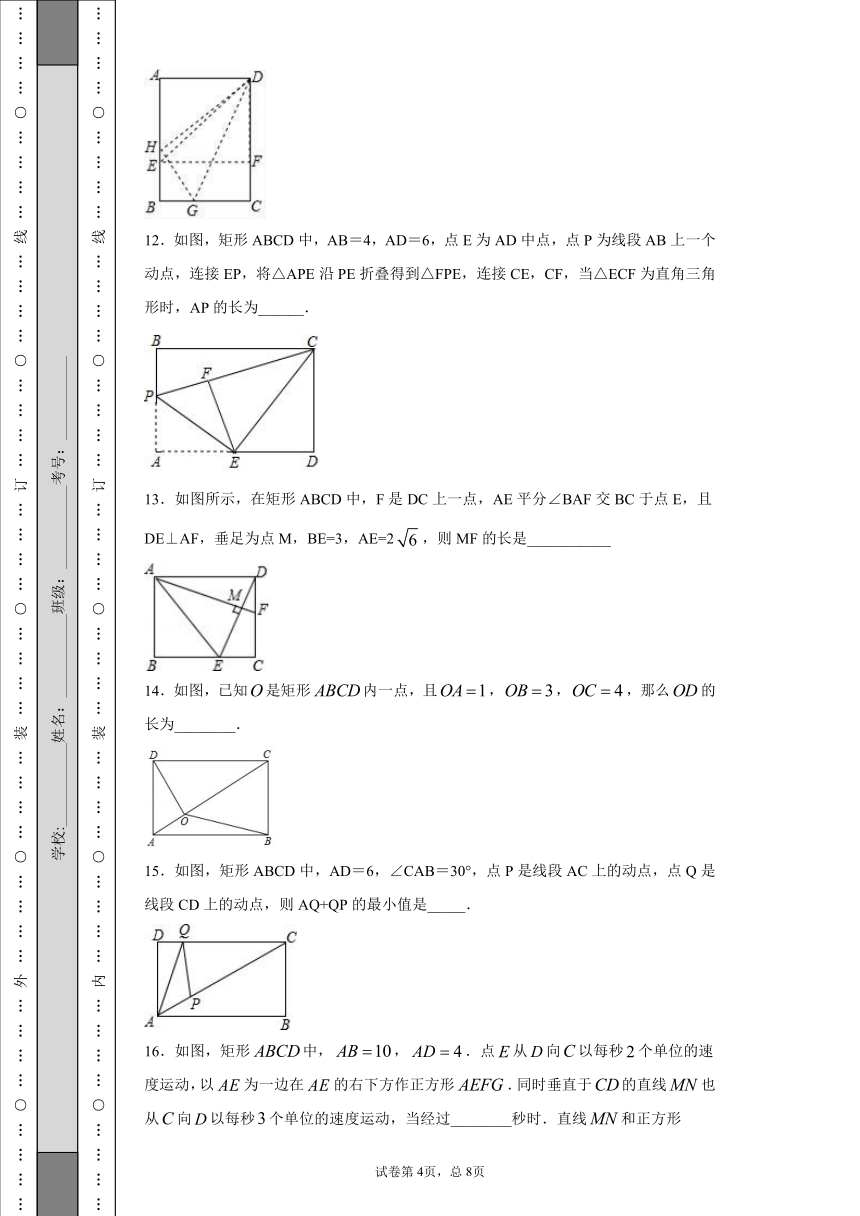
12.如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为______.
13.如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2,则MF的长是___________
14.如图,已知是矩形内一点,且,,,那么的长为________.
15.如图,矩形ABCD中,AD=6,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是_____.
16.如图,矩形中,,.点从向以每秒个单位的速度运动,以为一边在的右下方作正方形.同时垂直于的直线也从向以每秒个单位的速度运动,当经过________秒时.直线和正方形开始有公共点?
三、解答题
17.如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点终点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动,它们到达终点后停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ的面积是24cm2.
18.在菱形中,,点是射线上一动点,以为边向右侧作等边,点的位置随点的位置变化而变化.
(1)如图1,当点在菱形内部或边上时,连接,与的数量关系是 ,与的位置关系是 ;
(2)当点在菱形外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点在线段的延长线上时,连接,若 , ,求四边形的面积.
19.在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
20.如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2,CE=2,求线段AE的长.
21.如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.
(1)求证:AE=EF;
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,(1)中的结论是否仍然成立? ;(填“成立”或“不成立”);
(3)如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请证明,若不成立说明理由.
22.如图,矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB向点B移动(不与点A、B重合),一直到达点B为止;同时,点Q从点C出发沿CD向点D移动(不与点C、D重合).运动时间设为t秒.
(1)若点P、Q均以3cm/s的速度移动,则:AP= cm;QC= cm.(用含t的代数式表示)
(2)若点P为3cm/s的速度移动,点Q以2cm/s的速度移动,经过多长时间PD=PQ,使△DPQ为等腰三角形?
(3)若点P、Q均以3cm/s的速度移动,经过多长时间,四边形BPDQ为菱形?
23.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.动点P从点A开始沿折线AC﹣CB﹣BA运动,点P在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位.直线l从与AC重合的位置开始,以每秒个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
(1)当t=5秒时,点P走过的路径长为 ;当t= 秒时,点P与点E重合;
(2)当点P在AC边上运动时,连结PE,并过点E作AB的垂线,垂足为H.若以C、P、E为顶点的三角形与△EFH相似,试求线段EH的值;
(3)当点P在折线AC﹣CB﹣BA上运动时,作点P关于直线EF的对称点Q.在运动过程中,若形成的四边形PEQF为菱形,求t的值.
24.(1)如图①,点 M 是正方形 ABCD 的边 BC 上一点,点 N 是 CD 延长线上一点, 且BM=DN,则线段 AM 与 AN 的关系.
(2)如图②,在正方形 ABCD 中,点 E、F分别在边 BC、CD上,且∠EAF=45°,判断 BE,DF,EF 三条线段的数量关系,并说明理由.
(3)如图③,在四边形 ABCD中,AB=AD,∠BAD=90°,∠ABC+∠ADC=180°,点E、F分别在边 BC、CD 上,且∠EAF=45°,若 BD=5,EF=3,求四边形 BEFD 的周长.
参考答案
1.C【解析】∵四边形ABCD是正方形,∴AB=AD,∵△AEF是等边三角形,∴AE=AF,在Rt△ABE和Rt△ADF中,,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∵BC=DC,∴BC–BE=CD–DF,∴CE=CF,∴①说法正确;∵CE=CF,∴△ECF是等腰直角三角形,∴∠CEF=45°,∵∠AEF=60°,∴∠AEB=75°,∴②说法正确;如图,连接AC,交EF于G点,∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,∴DF≠FG,∴BE+DF≠EF,∴③说法错误;∵EF=2,∴CE=CF=,设正方形的边长为a,在Rt△ADF中,a2+(a–)2=4,解得a=,则a2=2+,∴S正方形ABCD=2+,④说法正确,∴正确的有①②④.故选C.
2.D【解析】①正确.理由:
∵AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴Rt△ABG≌Rt△AFG(HL);
②正确.理由:
∵∠BAG=∠FAG,∠DAE=∠FAE.
又∵∠BAD=90°,∴∠EAG=45°;
③正确.理由:
设DE=x,则EF=x,EC=12-x.在直角△ECG中,根据勾股定理,得:(12﹣x)2+62=(x+6)2,解得:x=4,∴DE=x=4,CE=12-x=8,∴CE=2DE;
④正确.理由:
∵CG=BG,BG=GF,∴CG=GF,∴∠GFC=∠GCF.
又∵Rt△ABG≌Rt△AFG,∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=∠GFC+∠GCF=2∠GFC=2∠GCF,∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF;
⑤正确.理由:
∵S△ECG=GC?CE=×6×8=24.
∵S△FCG===.
故选D.
3.A
【解析】如图1,作AE⊥BC于E,AF⊥CD于F,
,
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵两个矩形的宽都是3,
∴AE=AF=3,
∵S四边形ABCD=AE?BC=AF?CD,
∴BC=CD,
∴平行四边形ABCD是菱形.
如图2,
,
设AB=BC=x,则BE=9?x,
∵BC2=BE2+CE2,
∴x2=(9?x)2+32,
解得x=5,∴四边形ABCD面积的最大值是:5×3=15.故选A.
4.D【解析】∵AD=8,AB=6,四边形ABCD为矩形,∴BC=AD=8,∠B=90°,∴AC==10.
△EFC为直角三角形分两种情况:
①当∠EFC=90°时,如图1所示.
∵∠AFE=∠B=90°,∠EFC=90°,∴点F在对角线AC上,∴AE平分∠BAC,∴,即,∴BE=3;
②当∠FEC=90°时,如图2所示.
∵∠FEC=90°,∴∠FEB=90°,∴∠AEF=∠BEA=45°,∴四边形ABEF为正方形,∴BE=AB=6.
综上所述:BE的长为3或6.
故选D.
5.B【解析】第一个正方形的面积为1=20,
第二个正方形的面积为()2=2=21,
第三个正方形的边长为22,
…
第n个正方形的面积为2n﹣1,
故选B.
6.A【解析】①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∵在△APD和△AEB中,
∴△APD≌△AEB(SAS);
故此选项成立;
③∵△APD≌△AEB,
∴∠APD=∠AEB,
∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE=90°,
∴EB⊥ED;
故此选项成立;
②过B作BF⊥AE,交AE的延长线于F,
∵AE=AP,∠EAP=90°,
∴∠AEP=∠APE=45°,
又∵③中EB⊥ED,BF⊥AF,
∴∠FEB=∠FBE=45°,
又∵BE= ,
∴BF=EF= ,
故此选项正确;
④如图,连接BD,在Rt△AEP中,
∵AE=AP=1,
∴EP= ,
又∵PB=,
∴BE=,
∵△APD≌△AEB,
∴PD=BE=,
∴S△ABP+S△ADP=S△ABD﹣S△BDP=S正方形ABCD﹣×DP×BE=×(4+)﹣××=+.
故此选项不正确.
综上可知其中正确结论的序号是①②③,
故选:A.
7.B【解析】,,,
≌,故正确.
≌,
,.
,
,即,
为等腰直角三角形,
,故正确.
,,
.
.
,故错误;
,E为DC的中点,
,
依据勾股定理可知:,则,则,故错误.
故选:B.
8.C【解析】将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,
∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=15,
∴得出S1=8y+x,S2=4y+x,S3=x,
∴S1+S2+S3=3x+12y=15,即3x+12y=15,x+4y=5,
所以S2=x+4y=5,
故答案为5.
9.C【解析】∵AB=BC=CD=AD=4,∠A=∠C=60°,
∴△ABD,△BCD为等边三角形,∴∠A=∠BDC=60°.
∵将△BCD绕点B旋转到△BC'D'位置,
∴∠ABD'=∠DBC',且AB=BD,∠A=∠DBC',
∴△ABE≌△BFD,
∴AE=DF,BE=BF,∠AEB=∠BFD,
∴∠BED+∠BFD=180°.
故①正确,③错误;
∵∠ABD=60°,∠ABE=∠DBF,
∴∠EBF=60°.
故②正确;
∵△DEF的周长=DE+DF+EF=AD+EF=4+EF,
∴当EF最小时.∵△DEF的周长最小.
∵∠EBF=60°,BE=BF,∴△BEF是等边三角形,
∴EF=BE,
∴当BE⊥AD时,BE长度最小,即EF长度最小.
∵AB=4,∠A=60°,BE⊥AD,
∴EB=2,
∴△DEF的周长最小值为4+2.
故④正确.
故选C.
10.C【解析】正方形的边长为4,因为乙的速度是甲的速度的3倍,时间相同,甲乙所行的路程比为1:3,把正方形的每一条边平均分成2份,由题意知:
①第一次相遇甲乙行的路程和为8,甲行的路程为,乙行的路程为8-2=6,在AD边相遇;
②第二次相遇甲乙行的路程和为16,甲行的路程为,乙行的路程为16-4=12,在DC边相遇;
③第三次相遇甲乙行的路程和为16,甲行的路程为,乙行的路程为16-4=12,在CB边相遇;
④第四次相遇甲乙行的路程和为16,甲行的路程为,乙行的路程为16-4=12,在AB边相遇;
……
∴甲、乙相遇位置每四次为一个循环周期.可列表如下:
故选C.
11.3+2.【解析】设,则,
把翻折,点落在边上的点处,
,,,
四边形为正方形,
,
把翻折,点落在线段上的点处,折痕为,点在上,
,
,
,
在中,,
,
整理得,解得,(舍去),
即的长为.
故答案为:.
12.1或.【解析】分两种情况进行讨论:①如图所示,当∠CFE=90°时,△ECF是直角三角形.
由折叠可得:∠PFE=∠A=90°,AE=FE=DE,
∴∠CFP=180°,
即点P,F,C在一条直线上.
在Rt△CDE和Rt△CFE中,,
∴Rt△CDE≌Rt△CFE(HL),
∴CF=CD=4,设AP=FP=x,则BP=4﹣x,CP=x+4.
在Rt△BCP中,BP2+BC2=PC2,即(4﹣x)2+62=(x+4)2,
解得:x,即AP;
②如图所示,当∠CEF=90°时,△ECF是直角三角形.
过F作FH⊥AB于H,作FQ⊥AD于Q,则∠FQE=∠D=90°.
又∵∠FEQ+∠CED=90°=∠ECD+∠CED,
∴∠FEQ=∠ECD,
∴△FEQ∽△ECD,
∴,即,
解得:FQ,QE,
∴AQ=HF,AH,
设AP=FP=x,则HPx.
∵Rt△PFH中,HP2+HF2=PF2,
即(x)2+()2=x2,解得:x=1,即AP=1.
综上所述:AP的长为1或.
13.
【解析】∵AE平分∠BAF交BC于点E,且DE⊥AF,∠B=90°,
∴AB=AM,BE=EM=3,
又∵AE=2,
∴AM=,
设MD=a,MF=x,
∵在△ADM和△DFM中,∠AMD=∠DMF,∠ADM=∠DFM
∴△ADM∽△DFM,
∴,
∴DM2=AM?MF,
∴a2=x,
∵∠DMF=∠C,∠MDF=∠MDF,
∴△DMF∽△DCE,
∴,即:.
∴,
∴,
解之得:,
故答案是:.
14.【解析】如图,过O作EF⊥AD于E,交BC于F;过O作GH⊥DC于G,交AB于H.
设CF=x,FB=y,AH=s,HB=t,
∴OG=x,DG=s,
∴OF2=OB2-BF2=OC2-CF2,
即42-x2=32-y2,
∴x2-y2=16-9=7①
同理:OH2=12-s2=32-t2
∴t2-s2=32-12=8②
又∵OH2+HB2=OB2,即y2+t2=9;
①-②得(x2+s2)-(y2+t2)=-1,
∴OD2=x2+s2=(y2+t2)-1=9-1=8,
∴OD=2.
故答案为2.
15.6
【解析】
解:作点A关于直线CD的对称点E,作EP⊥AC于P,交CD于点Q.
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴DQ⊥AE,
∵DE=AD,
∴QE=QA,
∴QA+QP=QE+QP=EP,
∴此时QA+QP最短(垂线段最短),
∵∠CAB=30°,
∴∠DAC=60°,
在RT△APE中,∵∠APE=90°,AE=2AD=12,
∴EP=AE?sin60°=12× =6 .
故答案为:6.
16.
【解析】过F作FQ⊥DC于Q,
∵四边形AEFG是正方形,
∴∠AEF=90°,AE=EF,
∴∠DEA+∠FEQ=90°,
∵四边形ABCD是矩形,
∴∠D=90°,
∴∠DAE+∠DEA=90°,
∴∠FEQ=∠DAE,
在△ADE和△EQF中,
∵∠D=∠EQF=90°,∠DAE=∠FEQ,AE=EF,
∴△ADE≌△EQF,
∴AD=EQ=4,
当直线MN和正方形AEFG开始有公共点时,DQ+CM≥10,
∴2t+4+3t≥10,
解得t≥,
∴当经过秒时.直线MN和正方形AEFG开始有公共点.
故答案为:.
17.(1)3;(2)4.
【解析】(1)设t秒后点P、D的距离是点P、Q距离的2倍,
∴PD=2PQ
∵四边形ABCD是矩形
∴∠A=∠B=90°
∴PD2=AP2+AD2 ,PQ2=BP2+BQ2
∵PD2=4 PQ2,∴82+(2t)2=4[(10-2t)2+t2],
解得:t1=3,t2=7;
∵t=7时10-2t<0,∴t=3
(2) 设x秒后△DPQ的面积是24cm2,
∴
整理得x2-8x+16=0
解得x1=x2=4
即4秒后,△DPQ的面积是24cm2.
18.(1)BP=CE; CE⊥AD;(2)成立,理由见解析;(3) .
【解析】(1)①BP=CE,理由如下:
连接AC,
∵菱形ABCD,∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE ,∠PAE=60° ,
∴∠BAP=∠CAE,
∴△ABP≌△ACE,∴BP=CE;
②CE⊥AD ,
∵菱形对角线平分对角,
∴,
∵△ABP≌△ACE,
∴,
∵,
∴,
∴,
∴ ,
∴CF⊥AD ,即CE⊥AD;
(2)(1)中的结论:BP=CE,CE⊥AD 仍然成立,理由如下:
连接AC,
∵菱形ABCD,∠ABC=60°,
∴△ABC和△ACD都是等边三角形,
∴AB=AC,∠BAD=120° ,
∠BAP=120°+∠DAP,
∵△APE是等边三角形,
∴AP=AE , ∠PAE=60° ,
∴∠CAE=60°+60°+∠DAP=120°+∠DAP,
∴∠BAP=∠CAE,
∴△ABP≌△ACE,∴BP=CE,,
∴∠DCE=30° ,∵∠ADC=60°,
∴∠DCE+∠ADC=90° , ∴∠CHD=90° ,∴CE⊥AD,
∴(1)中的结论:BP=CE,CE⊥AD 仍然成立;
(3) 连接AC交BD于点O,CE,作EH⊥AP于H,
∵四边形ABCD是菱形,
∴AC⊥BD,BD平分∠ABC ,
∵∠ABC=60°,,
∴∠ABO=30° ,∴ , BO=DO=3,
∴BD=6,
由(2)知CE⊥AD,
∵AD∥BC,∴CE⊥BC,
∵ , ,
∴,
由(2)知BP=CE=8,∴DP=2,∴OP=5,
∴,
∵△APE是等边三角形,∴ , ,
∵,
∴,
=
=
=,
∴四边形ADPE的面积是 .
19.(1)证明见解析;(2)2,9.
【解析】感知:∵四边形ABCD是正方形,
∴AB=BC,∠BCE=∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵AF⊥BE,
∴∠ABE+∠BAF=90°,
∴∠BAF=∠CBE,
在△ABF和△BCE中,
,
∴△ABF≌△BCE(ASA);
探究:(1)如图②,
过点G作GP⊥BC于P,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=90°,
∴四边形ABPG是矩形,
∴PG=AB,∴PG=BC,
同感知的方法得,∠PGF=∠CBE,
在△PGF和△CBE中,
,
∴△PGF≌△CBE(ASA),
∴BE=FG;
(2)由(1)知,FG=BE,
连接CM,
∵∠BCE=90°,点M是BE的中点,
∴BE=2CM=2,
∴FG=2,
故答案为:2.
应用:同探究(2)得,BE=2ME=2CM=6,
∴ME=3,
同探究(1)得,CG=BE=6,
∵BE⊥CG,
∴S四边形CEGM=CG×ME=×6×3=9,故答案为:9.
20.(1)证明见解析;(2)证明见解析;(3)4.
【解析】(1)如图1.∵四边形ABFD是平行四边形,∴AB=DF.∵AB=AC,∴AC=DF.∵DE=EC,∴AE=EF.∵∠DEC=∠AEF=90°,∴△AEF是等腰直角三角形;
(2)如图2,连接EF,DF交BC于K.∵四边形ABFD是平行四边形,∴AB∥DF,∴∠DKE=∠ABC=45°,∴∠EKF=180°﹣∠DKE=135°,EK=ED.∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,∴∠EKF=∠ADE.∵∠DKC=∠C,∴DK=DC.∵DF=AB=AC,∴KF=AD.在△EKF和△EDA中,,∴△EKF≌△EDA(SAS),∴EF=EA,∠KEF=∠AED,∴∠FEA=∠BED=90°,∴△AEF是等腰直角三角形,∴AF=AE.
(3)如图3,当AD=AC=AB时,四边形ABFD是菱形,设AE交CD于H,依据AD=AC,ED=EC,可得AE垂直平分CD,而CE=2,∴EH=DH=CH=,Rt△ACH中,AH==3,∴AE=AH+EH=4.
21.(1)证明见解析;(2)成立;(3)成立,证明见解析.
【解析】(1)证明:取AB中点M,连接EM,
∵AB=BC,E为BC中点,M为AB中点,
∴AM=CE=BE,
∴∠BME=∠BME=45°,
∴∠AME=135°=∠ECF,
∵∠B=90°,
∴∠BAE+∠AEB=90°,
∵∠AEF=90°,
∴∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
在△AME和△ECF中,
∴△AME≌△ECF(ASA),
∴AE=EF;
(2)成立,理由是:如图,在AB上截取BM=BE,连接ME,
∵∠B=90°,
∴∠BME=∠BEM=45°,
∴∠AME=135°=∠ECF,
∵AB=BC,BM=BE,
∴AM=EC,
在△AME和△ECF中,
∴△AME≌△ECF(ASA),
∴AE=EF;
(3)成立.
证明:如图,在BA的延长线上取一点N.使AN=CE,连接NE,
∴BN=BE,
∴∠N=∠NEC=45°,
∵CF平分∠DCG,
∴∠FCE=45°,
∴∠N=∠ECF,
∵四边形ABCD是正方形,
∴AD∥BE,
∴∠DAE=∠BEA,即∠DAE+90°=∠BEA+90°,
∴∠NAE=∠CEF,
∴△ANE≌△ECF(ASA),
∴AE=EF.
22.(1)3t,3t;(2)当t=2时,PD=PQ,△DPQ为等腰三角形;(3)当 时,四边形BPDQ是菱形.
【解析】(1) , ;
(2)过点P作PE⊥CD于点E ∴ ∠PED=90° ∵ PD=PQ ∴ DE=DQ
在矩形ABCD中,∠A=∠ADE=90°,CD=AB=16㎝
∴ 四边形PEDA是矩形 ∴ DE=AP=3 又∵ CQ=2 ∴ DQ=16-
∴ 由DE=DQ ∴ ∴
∴ 当时,PD=PQ,△DPQ为等腰三角形
(3)在矩形ABCD中,AB=CD,AB∥CD,AD=BC,依题知AP=CQ=3
∴ PB=DQ ∴ 四边形BPDQ是平行四边形
当PD=PB时,四边形BPDQ是菱形 ∴ PB=AB-AP=16-3
在Rt△APD中,PD=
由PD=PB ∴ 即: 解得:
∴ 当时,四边形BPDQ是菱形.
23.(1)19;3 ;(2)EH=或;(3)满足要求的t值为t=,
【解析】
(1)19;3 (2)注意到△EFH为直角边3:4的直角三角形,若△CPE与之相似,也应如此.
而CP=6-3t,CE=t,分别令CP:CE=3:4或4:3,解得t=或
当t=时,EH=;当t=时,EH=
(3)当点P在AC上运动时,若四边形PEQF为菱形,连结PQ,则PQ垂直平分EF.
故有EF=2CP,于是 (8-t)=2(6-3t),解得t=<2,符合
当点 P在CB上运动时,显然不构成四边形.
当点 P在BA上运动时,若四边形PEQF为菱形,有4<t<,且PE=PF.
在Rt△BEF中,可知P为BF的中点,故有BF=2BP,于是 (8-t)=2×5(t-4),
解得t=,也符合
综上所述,满足要求的t值有两个,t=,
24.(1)结论:AM=AN,AM⊥AN.理由见解析;(2)BE+DF=EF;(3)四边形BEFD的周长为11.
【解析】(1)结论:AM=AN,AM⊥AN.
理由:∵四边形 ABCD 是正方形,
∴AB=AD,∠B=∠ADN=∠BAD=90°,
∵BM=DN,
∴△ABM≌△ADN,
∴AM=AN,∠BAM=∠DAN,
∴∠AMN=∠BAD=90°,
∴AM⊥AN,
(2)如图②中,过点 A 作 AG⊥AE 交 CD 延长线于点 G.
∵四边形 ABCD 为正方形,
∴AB=AD,∠B=∠BAD=∠ADC=90°.
∴∠B=∠ADG=90°,∠BAE+∠EAD=90°.
∵AG⊥AE,∴∠DAG+∠EAD=90°.
∴∠BAE=∠DAG.
在△ABE 和△ADG 中,
,
∴△ABE≌△ADG.
∴AE=AG,BE=DG.
∵∠EAF=45°,AG⊥AE,
∴∠EAF=∠GAF=45°.
在△FAE 和△FAG 中,
,
∴△AEF≌△AGF.
∴EF=FG.
∵FG=DF+DG=DF+BE,
∴BE+DF=EF.
(3)如图③中,过点 A 作 AG⊥AE 交 CD 延长线于点 G.
∵AB=AD,∠ABC+∠ADC=180°,∠ADG+∠ADC=180°
∴∠ABE=∠ADG,
∵AG⊥AE,∴∠DAG+∠EAD=90°.
∵∠BAE+∠EAD=90°
∴∠BAE=∠DAG.
在△ABE 和△ADG 中,
,
∴△ABE≌△ADG.
∴AE=AG,BE=DG.
∵∠EAF=45°,AG⊥AE,
∴∠EAF=∠GAF=45°.
在△FAE 和△FAG 中,
,
∴△AEF≌△AGF.
∴EF=FG.
∵FG=DF+DG=DF+BE,
∴BE+DF=EF.
∴四边形BEFD的周长为EF+(BE+DF)+DB=3+3+5=11.
试卷第1页,总3页
试卷第1页,总3页
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
