浙教版2020年八年级数学下学期2.3 一元二次方程的应用同步练习卷解析版
文档属性
| 名称 | 浙教版2020年八年级数学下学期2.3 一元二次方程的应用同步练习卷解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 260.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 22:47:08 | ||
图片预览




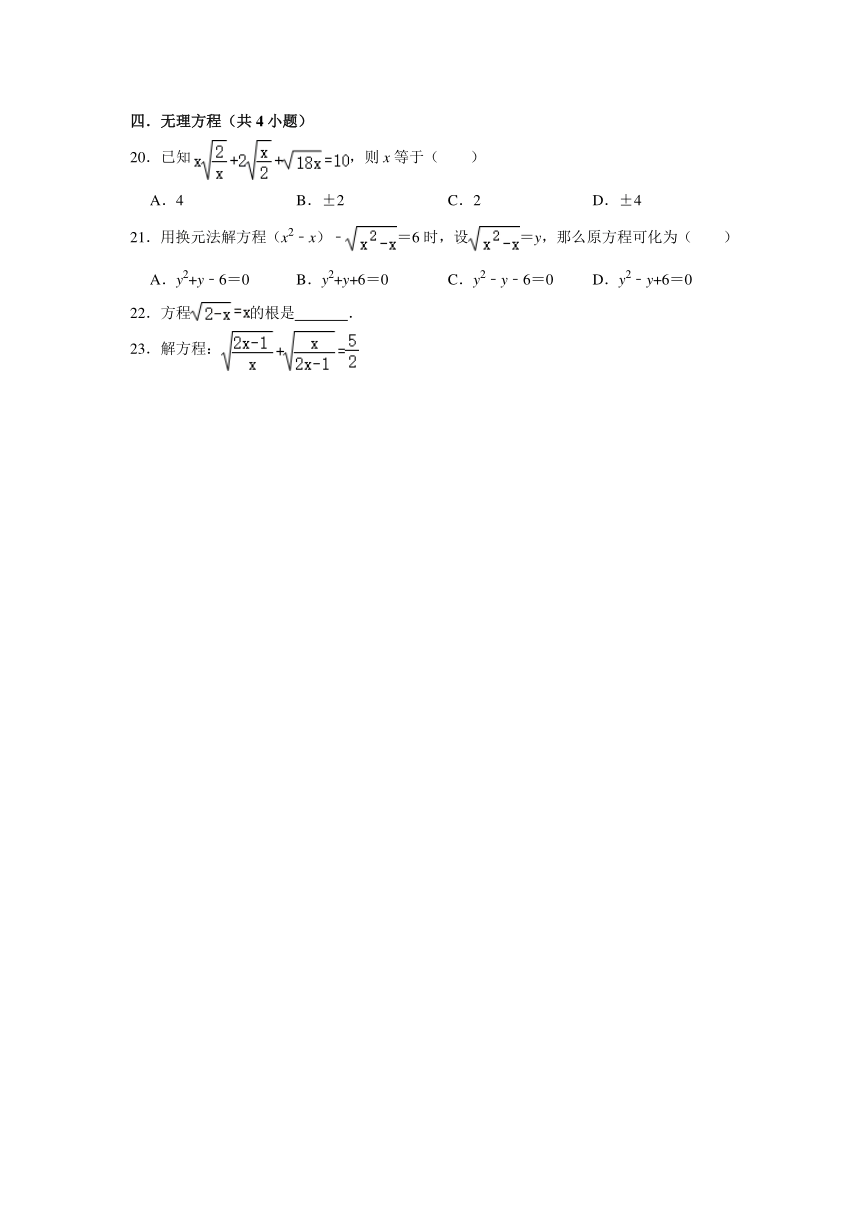
文档简介
浙教版八年级下学期《2.3 一元二次方程的应用》2020年同步练习卷
一.由实际问题抽象出一元二次方程(共9小题)
1.某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.560(1+x)2=315 B.560(1﹣x)2=315
C.560(1﹣2x)2=315 D.560(1﹣x2)=315
2.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1056张照片,如果全班有x名同学,根据题意,列出方程为( )
A.x(x+1)=1056 B.x(x﹣1)=1056×2
C.x(x﹣1)=1056 D.2x(x+1)=1056
3.学校要组织足球比赛.赛制为单循环形式(每两队之间赛一场).计划安排21场比赛,应邀请多少个球队参赛?设邀请x个球队参赛.根据题意,下面所列方程正确的是( )
A.x2=21 B.x(x﹣1)=21
C.x2=21 D.x(x﹣1)=21
4.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是( )
A.(32﹣2x)(20﹣x)=570
B.32x+2×20x=32×20﹣570
C.(32﹣x)(20﹣x)=32×20﹣570
D.32x+2×20x﹣2x2=570
5.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15
C.(x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=15
6.股票每天的涨、跌幅均不能超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.已知一只股票某天跌停,之后两天时间又涨回到原价.若这两天此股票股价的平均增长率为x,则x满足的方程是( )
A.(1+x)2= B.(1+x)2=
C.1+2x= D.1+2x=
7.宾馆有50间房供游客居住,当毎间房每天定价为180元时,宾馆会住满;当毎间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的毎间房每天支出20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价定为x元.则有( )
A.(180+x﹣20)(50﹣)=10890
B.(x﹣20)(50﹣)=10890
C.x(50﹣)﹣50×20=10890
D.(x+180)(50﹣)﹣50×20=10890
8.某公司今年销售一种产品,一月份获得利润10万元,由于产品畅销,利润逐月增加,一季度共获利36.4万元,已知2月份和3月份利润的月增长率相同.设2,3月份利润的月增长率为x,那么x满足的方程为( )
A.10(1+x)2=36.4
B.10+10(1+x)2=36.4
C.10+10(1+x)+10(1+2x)=36.4
D.10+10(1+x)+10(1+x)2=36.4
9.2010年某市政府投资2亿元人民币建设了廉租房8万平方米,预计到2012年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.设每年市政府投资的增长率为x,根据题意,列出方程为( )
A.2(1+x)2=9.5 B.2(1+x)+2(1+x)2=9.5
C.2+2(1+x)+2(1+x)2=9.5 D.8+8(1+x)+8(1+x)2=9.5
二.一元二次方程的应用(共5小题)
10.在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )
A.9人 B.10人 C.11人 D.12人
11.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
12.水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
13.已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
14.已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于6cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于5cm?
(3)在(1)中,△PQB的面积能否等于8cm2?说明理由.
三.高次方程(共5小题)
15.二元二次方程组的解是 .
16.解方程组:.
17.若(x2+y2)(x2+y2﹣1)=6,则x2+y2= .
18.九年义务教育三年制初级中学教科书《代数》第三册第52页的例2是这样的:“解方程x4﹣6x2+5=0”.这是一个一元四次方程,根据该方程的特点,它的解法通常是:设x2=y,那么x4=y2,于是原方程可变为y2﹣6y+5=0…①,解这个方程得:y1=1,y2=5.当y=1时,x2=1,∴x=±1;当y=5时,x2=5,∴.所以原方程有四个根:x1=1,x2=﹣1,x3=,x4=﹣.
(1)在由原方程得到方程①的过程中,利用 法达到降次的目的,体现了转化的数学思想.
(2)解方程(x2﹣x)2﹣4(x2﹣x)﹣12=0时,若设y=x2﹣x,则原方程可化为 .
19.阅读材料:为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1看作一个整体,然后设x2﹣1=y…①,
那么原方程可化为y2﹣5y+4=0,
解得y1=1,y2=4.
当y=1时,x2﹣1=1,∴x2=2,∴x=±;
当y=4时,x2﹣1=4,∴x2=5,∴x=±,
故原方程的解为x1=,x2=,x3=,x4=.
解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用 法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解方程x4﹣x2﹣6=0.
四.无理方程(共4小题)
20.已知,则x等于( )
A.4 B.±2 C.2 D.±4
21.用换元法解方程(x2﹣x)﹣=6时,设=y,那么原方程可化为( )
A.y2+y﹣6=0 B.y2+y+6=0 C.y2﹣y﹣6=0 D.y2﹣y+6=0
22.方程的根是 .
23.解方程:
参考答案与试题解析
一.由实际问题抽象出一元二次方程(共9小题)
1.某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.560(1+x)2=315 B.560(1﹣x)2=315
C.560(1﹣2x)2=315 D.560(1﹣x2)=315
【分析】设每次降价的百分率为x,根据降价后的价格=降价前的价格(1﹣降价的百分率),则第一次降价后的价格是560(1﹣x),第二次后的价格是560(1﹣x)2,据此即可列方程求解.
【解答】解:设每次降价的百分率为x,由题意得:
560(1﹣x)2=315,
故选:B.
2.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1056张照片,如果全班有x名同学,根据题意,列出方程为( )
A.x(x+1)=1056 B.x(x﹣1)=1056×2
C.x(x﹣1)=1056 D.2x(x+1)=1056
【分析】如果全班有x名同学,那么每名同学要送出(x﹣1)张,共有x名学生,那么总共送的张数应该是x(x﹣1)张,即可列出方程.
【解答】解:∵全班有x名同学,
∴每名同学要送出(x﹣1)张;
又∵是互送照片,
∴总共送的张数应该是x(x﹣1)=1056.
故选:C.
3.学校要组织足球比赛.赛制为单循环形式(每两队之间赛一场).计划安排21场比赛,应邀请多少个球队参赛?设邀请x个球队参赛.根据题意,下面所列方程正确的是( )
A.x2=21 B.x(x﹣1)=21
C.x2=21 D.x(x﹣1)=21
【分析】赛制为单循环形式(每两队之间都赛一场),x个球队比赛总场数=.即可列方程.
【解答】解:设有x个队,每个队都要赛(x﹣1)场,但两队之间只有一场比赛,由题意得:
x(x﹣1)=21,
故选:B.
4.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是( )
A.(32﹣2x)(20﹣x)=570
B.32x+2×20x=32×20﹣570
C.(32﹣x)(20﹣x)=32×20﹣570
D.32x+2×20x﹣2x2=570
【分析】六块矩形空地正好能拼成一个矩形,设道路的宽为xm,根据草坪的面积是570m2,即可列出方程.
【解答】解:设道路的宽为xm,根据题意得:(32﹣2x)(20﹣x)=570,
故选:A.
5.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15
C.(x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=15
【分析】根据已知假设每盆花苗增加x株,则每盆花苗有(x+3)株,得出平均单株盈利为(4﹣0.5x)元,由题意得(x+3)(4﹣0.5x)=15即可.
【解答】解:设每盆应该多植x株,由题意得
(3+x)(4﹣0.5x)=15,
故选:A.
6.股票每天的涨、跌幅均不能超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.已知一只股票某天跌停,之后两天时间又涨回到原价.若这两天此股票股价的平均增长率为x,则x满足的方程是( )
A.(1+x)2= B.(1+x)2=
C.1+2x= D.1+2x=
【分析】股票一次跌停就跌到原来价格的90%,再从90%的基础上涨到原来的价格,且涨幅只能≤10%,所以至少要经过两天的上涨才可以.设平均每天涨x,每天相对于前一天就上涨到1+x.
【解答】解:假设股票的原价是1,设平均每天涨x.
则90%(1+x)2=1,
即(1+x)2=,
故选:B.
7.宾馆有50间房供游客居住,当毎间房每天定价为180元时,宾馆会住满;当毎间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的毎间房每天支出20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价定为x元.则有( )
A.(180+x﹣20)(50﹣)=10890
B.(x﹣20)(50﹣)=10890
C.x(50﹣)﹣50×20=10890
D.(x+180)(50﹣)﹣50×20=10890
【分析】设房价定为x元,根据利润=房价的净利润×入住的房间数可得.
【解答】解:设房价定为x元,
根据题意,得(x﹣20)(50﹣)=10890.
故选:B.
8.某公司今年销售一种产品,一月份获得利润10万元,由于产品畅销,利润逐月增加,一季度共获利36.4万元,已知2月份和3月份利润的月增长率相同.设2,3月份利润的月增长率为x,那么x满足的方程为( )
A.10(1+x)2=36.4
B.10+10(1+x)2=36.4
C.10+10(1+x)+10(1+2x)=36.4
D.10+10(1+x)+10(1+x)2=36.4
【分析】等量关系为:一月份利润+一月份的利润×(1+增长率)+一月份的利润×(1+增长率)2=36.4,把相关数值代入计算即可.
【解答】解:设二、三月份的月增长率是x,依题意有
10+10(1+x)+10(1+x)2=36.4,
故选:D.
9.2010年某市政府投资2亿元人民币建设了廉租房8万平方米,预计到2012年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.设每年市政府投资的增长率为x,根据题意,列出方程为( )
A.2(1+x)2=9.5 B.2(1+x)+2(1+x)2=9.5
C.2+2(1+x)+2(1+x)2=9.5 D.8+8(1+x)+8(1+x)2=9.5
【分析】设每年市政府投资的增长率为x.根据到2012年底三年共累计投资9.5亿元人民币建设廉租房,列方程求解.
【解答】解:(1)设每年市政府投资的增长率为x,
根据题意,得:2+2(1+x)+2(1+x)2=9.5.
故选:C.
二.一元二次方程的应用(共5小题)
10.在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )
A.9人 B.10人 C.11人 D.12人
【分析】设参加酒会的人数为x人,根据每两人都只碰一次杯且一共碰杯55次,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
【解答】解:设参加酒会的人数为x人,
根据题意得:x(x﹣1)=55,
整理,得:x2﹣x﹣110=0,
解得:x1=11,x2=﹣10(不合题意,舍去).
答:参加酒会的人数为11人.
故选:C.
11.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
【分析】设矩形猪舍垂直于住房墙一边长为xm可以得出平行于墙的一边的长为(25﹣2x+1)m.根据矩形的面积公式建立方程求出其解就可以了.
【解答】解:设矩形猪舍垂直于住房墙一边长为xm可以得出平行于墙的一边的长为(25﹣2x+1)m,由题意得
x(25﹣2x+1)=80,
化简,得x2﹣13x+40=0,
解得:x1=5,x2=8,
当x=5时,26﹣2x=16>12(舍去),当x=8时,26﹣2x=10<12,
答:所围矩形猪舍的长为10m、宽为8m.
12.水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 100+200x 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
【分析】(1)销售量=原来销售量+下降销售量,据此列式即可;
(2)根据销售量×每斤利润=总利润列出方程求解即可.
【解答】解:(1)将这种水果每斤的售价降低x元,则每天的销售量是100+×20=100+200x(斤);
(2)根据题意得:(4﹣2﹣x)(100+200x)=300,
解得:x=或x=1,
当x=时,销售量是100+200×=200<260;
当x=1时,销售量是100+200=300(斤).
∵每天至少售出260斤,
∴x=1.
答:张阿姨需将每斤的售价降低1元.
13.已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
【分析】(1)直接将x=﹣1代入得出关于a,b的等式,进而得出a=b,即可判断△ABC的形状;
(2)利用根的判别式进而得出关于a,b,c的等式,进而判断△ABC的形状;
(3)利用△ABC是等边三角形,则a=b=c,进而代入方程求出即可.
【解答】解:(1)△ABC是等腰三角形;
理由:∵x=﹣1是方程的根,
∴(a+c)×(﹣1)2﹣2b+(a﹣c)=0,
∴a+c﹣2b+a﹣c=0,
∴a﹣b=0,
∴a=b,
∴△ABC是等腰三角形;
(2)∵方程有两个相等的实数根,
∴(2b)2﹣4(a+c)(a﹣c)=0,
∴4b2﹣4a2+4c2=0,
∴a2=b2+c2,
∴△ABC是直角三角形;
(3)当△ABC是等边三角形,∴(a+c)x2+2bx+(a﹣c)=0,可整理为:
2ax2+2ax=0,
∴x2+x=0,
解得:x1=0,x2=﹣1.
14.已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于6cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于5cm?
(3)在(1)中,△PQB的面积能否等于8cm2?说明理由.
【分析】(1)设经过x秒钟,△PBQ的面积等于6平方厘米,根据点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,表示出BP和BQ的长可列方程求解.
(2)根据PQ=5,利用勾股定理BP2+BQ2=PQ2,求出即可;
(3)通过判定得到的方程的根的判别式即可判定能否达到8cm2.
【解答】解:(1)设 经过x秒以后△PBQ面积为6
×(5﹣x)×2x=6
整理得:x2﹣5x+6=0
解得:x=2或x=3
答:2或3秒后△PBQ的面积等于6cm2
(2)当PQ=5时,在Rt△PBQ中,∵BP2+BQ2=PQ2,
∴(5﹣t)2+(2t)2=52,
5t2﹣10t=0,
t(5t﹣10)=0,
t1=0(舍弃),t2=2,
∴当t=2时,PQ的长度等于5cm.
(3)设经过x秒以后△PBQ面积为8,
×(5﹣x)×2x=8
整理得:x2﹣5x+8=0
△=25﹣32=﹣7<0
∴△PQB的面积不能等于8cm2.
三.高次方程(共5小题)
15.二元二次方程组的解是 .
【分析】由(1)得,x=3﹣y,代入(2)得(3﹣y)y=10,整理后求解.
【解答】解:由(1)得,x=3﹣y,
代入(2)得(3﹣y)y=10,
整理得:(y﹣5)(y+2)=0,
解得y=5或y=﹣2,
当y=5时,x=﹣2;
当y=﹣2时,x=5.
所以原方程组的解为:.
故本题答案为:,.
16.解方程组:.
【分析】用代入法即可解答,把①化为x=1+y,代入②得(1+y)2+2y+3=0即可.
【解答】解:
由①得y=x﹣2③
把③代入②,得x2﹣2x(x﹣2)﹣3(x﹣2)2=0,
即x2﹣4x+3=0
解这个方程,得x1=3,x2=1
代入③中,得或.
∴原方程组的解为或.
17.若(x2+y2)(x2+y2﹣1)=6,则x2+y2= 3 .
【分析】此题可用换元法求解.设x2+y2=z(z>0),则原式可化为z(z﹣1)=6,然后求得z的值.
【解答】解:设x2+y2=z(z>0),则原式可化为z(z﹣1)=6,
即z2﹣z﹣6=0,
解得:z=﹣2(舍去),z=3,
故有:x2+y2=3.
故答案为:3.
18.九年义务教育三年制初级中学教科书《代数》第三册第52页的例2是这样的:“解方程x4﹣6x2+5=0”.这是一个一元四次方程,根据该方程的特点,它的解法通常是:设x2=y,那么x4=y2,于是原方程可变为y2﹣6y+5=0…①,解这个方程得:y1=1,y2=5.当y=1时,x2=1,∴x=±1;当y=5时,x2=5,∴.所以原方程有四个根:x1=1,x2=﹣1,x3=,x4=﹣.
(1)在由原方程得到方程①的过程中,利用 换元 法达到降次的目的,体现了转化的数学思想.
(2)解方程(x2﹣x)2﹣4(x2﹣x)﹣12=0时,若设y=x2﹣x,则原方程可化为 y2﹣4y﹣12=0 .
【分析】(1)用一个字母表示一个较复杂的代数式的方法叫换元法.
(2)用y代替x2﹣x即可.
【解答】解:(1)在由原方程得到方程①的过程中,利用换元法达到降次的目的,体现了转化的数学思想.
(2)解方程(x2﹣x)2﹣4(x2﹣x)﹣12=0时,若设y=x2﹣x,则原方程可化为y2﹣4y﹣12=0.
19.阅读材料:为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1看作一个整体,然后设x2﹣1=y…①,
那么原方程可化为y2﹣5y+4=0,
解得y1=1,y2=4.
当y=1时,x2﹣1=1,∴x2=2,∴x=±;
当y=4时,x2﹣1=4,∴x2=5,∴x=±,
故原方程的解为x1=,x2=,x3=,x4=.
解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用 换元 法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解方程x4﹣x2﹣6=0.
【分析】本题主要利用换元法来解方程.
【解答】解:(1)换元法;
(2)设x2=y,那么原方程可化为y2﹣y﹣6=0,
解得y1=3,y2=﹣2,
当y=3时,x2=3,
∴x=±,
当y=﹣2时,x2=﹣2不符合题意,故舍去.
∴原方程的解为:x1=,x2=.
四.无理方程(共4小题)
20.已知,则x等于( )
A.4 B.±2 C.2 D.±4
【分析】已知,先化简再求值即可得出答案.
【解答】解:已知,∴x>0,
∴原式可化简为:++3=10,
∴=2,
两边平方得:2x=4,
∴x=2,
故选:C.
21.用换元法解方程(x2﹣x)﹣=6时,设=y,那么原方程可化为( )
A.y2+y﹣6=0 B.y2+y+6=0 C.y2﹣y﹣6=0 D.y2﹣y+6=0
【分析】本题中设=y,需要注意的是用来换元的式子为设,则x2﹣x=y2.
【解答】解:设=y,则方程为y2﹣y﹣6=0.
故选:C.
22.方程的根是 x=1 .
【分析】把方程两边平方去根号后即可转化成整式方程,解方程即可求得x的值,然后进行检验即可.
【解答】解:两边平方得:2﹣x=x2,
整理得:x2+x﹣2=0,
解得:x=1或﹣2.
经检验:x=1是方程的解,x=﹣2不是方程的解.
故答案是:x=1.
23.解方程:
【分析】此方程可用换元法解方程.设=y,则=.
【解答】解:设=y,则=,原方程可化为y+=,
两边同时乘以2y得,2y2﹣5y+2=0
(y﹣2)(2y﹣1)=0,
解得y=2或y=,
①当y=2时,=2,
两边平方得,2x﹣1=4x,
解得:x=﹣;
②当y=时,=,
两边平方得,8x﹣4=x,
解得x=.
检验:把x=﹣,x=,分别代入x(2x﹣1),均不为0,都是原方程的解.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
