2.3.2 一元二次方程的应用同步测试题(含解析)
文档属性
| 名称 | 2.3.2 一元二次方程的应用同步测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 12:50:17 | ||
图片预览




文档简介
2.3(2) 一元二次方程的应用测试卷
(时间45分钟 满分100分)
一.选择题(每小题7分,共42分)
1.(2019秋?江津区期中)从正方形的铁皮上,截去2cm宽的一条长方形,余下的面积是48cm2,则原来的正方形铁皮的边长是( )
A.7cm B.8cm C.9cm D.10cm
2.(2019秋?覃塘区期中)若一个直角三角形的两条直角边长之和为14,面积为24,则其斜边的长是( )
A.2 B.4 C.8 D.10
3.(2019秋?锡山区期中)如图,在长20m、宽18m的矩形草坪上,修筑同样宽的三条(横向一条,纵向两条矩形)道路,要使草坪面积达到306m2,则道路宽度是( )
A.27m B.26m C.2m D.1m
4.(2018秋?金凤区校级期中)如图,在一块长为30m,宽为24m的矩形空地上,修建同样宽的两条互相垂直的小路,其余部分建成花园,已知小路的占地面积为53m2,那么小路的宽为多少?( )
A.1m B.1.5m C.2m D.2.5m
5.(2019秋?越秀区校级月考)如图Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,动点P从点A出发沿AB边以1cm/秒的速度向点B匀速移动,同时,点Q从点B出发沿BC边以2cm/秒的速度向点C匀速移动,当P、Q两点中有一个点到达终点时另一个点也停止运动.运动( )秒后,△PBQ面积为5cm2.
A.0.5 B.1 C.5 D.1或5
6.(2018秋?高邮市校级月考)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.若苗圃园的面积为72平方米,则x为( )
A.12 B.10 C.15 D.8
二.填空题(每小题7分,共28分)
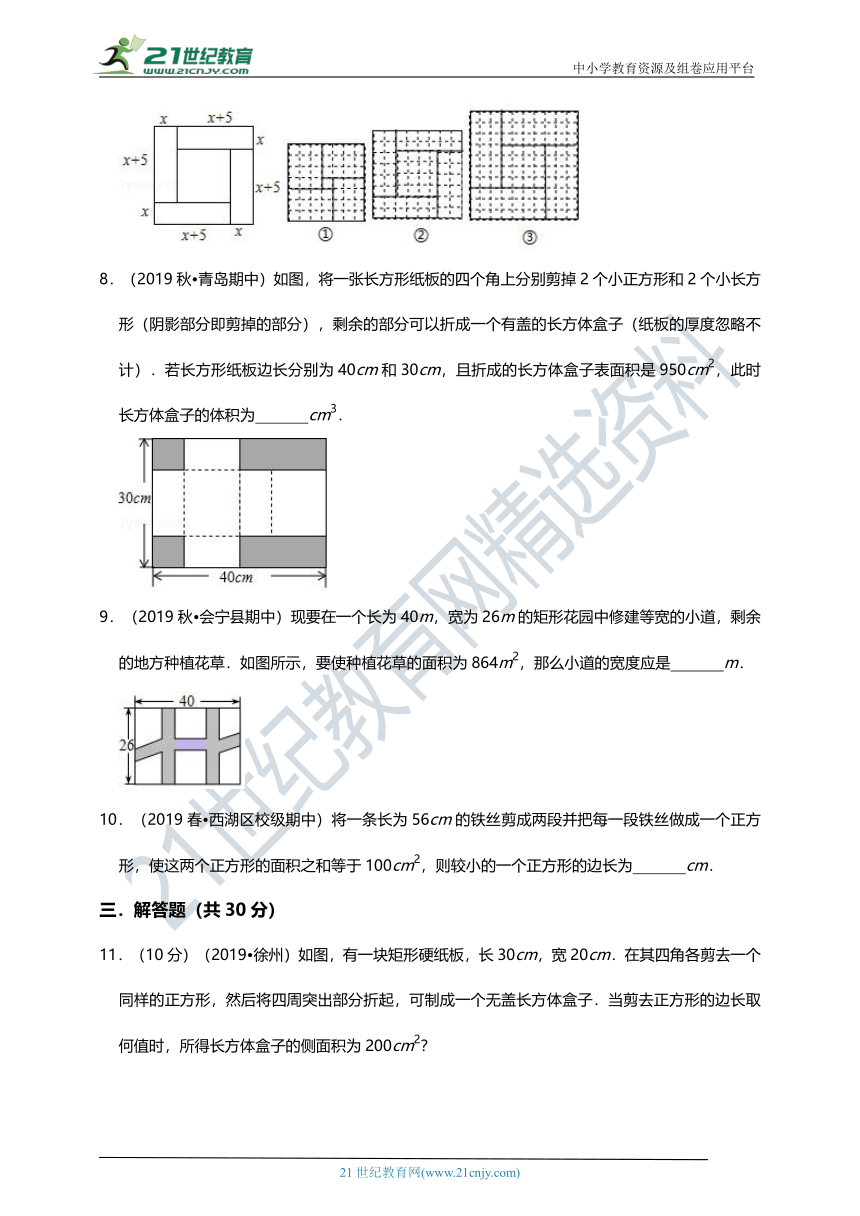
7.(2019?宁夏)你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢!以方程x2+5x﹣14=0即x(x+5)=14为例加以说明.数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图)中大正方形的面积是(x+x+5)2,其中它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,据此易得x=2.那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程x2﹣4x﹣12=0的正确构图是 .(只填序号)
8.(2019秋?青岛期中)如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm,且折成的长方体盒子表面积是950cm2,此时长方体盒子的体积为 cm3.
9.(2019秋?会宁县期中)现要在一个长为40m,宽为26m的矩形花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为864m2,那么小道的宽度应是 m.
10.(2019春?西湖区校级期中)将一条长为56cm的铁丝剪成两段并把每一段铁丝做成一个正方形,使这两个正方形的面积之和等于100cm2,则较小的一个正方形的边长为 cm.
三.解答题(共30分)
11.(10分)(2019?徐州)如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?
12.(10分)(2019?襄阳)改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为112m2,则小路的宽应为多少?
13.(10分)(2019?南京)某地计划对矩形广场进行扩建改造.如图,原广场长50m,宽40m,要求扩充后的矩形广场长与宽的比为3:2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米100元.如果计划总费用642000元,扩充后广场的长和宽应分别是多少米?
2.3(2) 一元二次方程的应用测试卷
参考答案与试题解析
一.选择题
1.(2019秋?江津区期中)从正方形的铁皮上,截去2cm宽的一条长方形,余下的面积是48cm2,则原来的正方形铁皮的边长是( )
A.7cm B.8cm C.9cm D.10cm
【分析】设原来的正方形铁皮的边长为xcm,利用余下的面积=正方形的面积﹣剪去长方形的面积,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
【解答】解:设原来的正方形铁皮的边长为xcm,
依题意,得:x2﹣2x=48,
解得:x1=8,x2=﹣6(不合题意,舍去).
故选:B.
2.(2019秋?覃塘区期中)若一个直角三角形的两条直角边长之和为14,面积为24,则其斜边的长是( )
A.2 B.4 C.8 D.10
【分析】设一边长为x,然后表示出另一边,然后利用直角三角形的面积的计算方法列出方程即可;然后再根据勾股定理求得斜边长.
【解答】解:设其中一条直角边的长为x,则另一条直角边为(14﹣x),根据题意得:x(14﹣x)=24,
整理得:x2﹣14x+48=0.
解得x1=6,x2=8,
所以斜边长为:=10.
故选:D.
3.(2019秋?锡山区期中)如图,在长20m、宽18m的矩形草坪上,修筑同样宽的三条(横向一条,纵向两条矩形)道路,要使草坪面积达到306m2,则道路宽度是( )
A.27m B.26m C.2m D.1m
【分析】设道路的宽度为xm,将剩余部分合成矩形,利用矩形的面积公式及草坪面积为306m2,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.
【解答】解:设道路的宽度为xm,
根据题意得:(20﹣2x)(18﹣x)=306,
化简得:x2﹣28x+27=0,
解得:x1=1,x2=27.
∵20﹣2x>0,
∴x<10,
∴x=1.
故选:D.
4.(2018秋?金凤区校级期中)如图,在一块长为30m,宽为24m的矩形空地上,修建同样宽的两条互相垂直的小路,其余部分建成花园,已知小路的占地面积为53m2,那么小路的宽为多少?( )
A.1m B.1.5m C.2m D.2.5m
【分析】把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程求解即可.
【解答】解:设道路的宽应为x米,由题意有
(30﹣x)(24﹣x)=30×24﹣53,
解得:x=53(舍去)或x=1.
答:修建的路宽为1米.
故选:A.
5.(2019秋?越秀区校级月考)如图Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,动点P从点A出发沿AB边以1cm/秒的速度向点B匀速移动,同时,点Q从点B出发沿BC边以2cm/秒的速度向点C匀速移动,当P、Q两点中有一个点到达终点时另一个点也停止运动.运动( )秒后,△PBQ面积为5cm2.
A.0.5 B.1 C.5 D.1或5
【分析】设经过x秒钟,使△PBQ的面积为8cm2,得到BP=6﹣x,BQ=2x,根据三角形的面积公式得出方程×(6﹣x)×2x=5,求出即可.
【解答】解:设经过x秒钟,使△PBQ的面积为5cm2,
BP=6﹣x,BQ=2x,
∵∠B=90°,
∴BP×BQ=5,
∴×(6﹣x)×2x=5,
∴x1=1,x2=5(舍去),
答:如果点P、Q分别从A、B同时出发,经过1秒钟,使△PBQ的面积为5cm2.
故选:B.
6.(2018秋?高邮市校级月考)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.若苗圃园的面积为72平方米,则x为( )
A.12 B.10 C.15 D.8
【分析】根据等量关系列方程求解即可.
【解答】解:根据题意得:x×(30﹣2x)=72
解得:x1=12,x2=3
当x=12时,30﹣2x=6<18
当x=3时,30﹣2x=24>18(不合题意舍去)
故选:A.
二.填空题
7.(2019?宁夏)你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢!以方程x2+5x﹣14=0即x(x+5)=14为例加以说明.数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图)中大正方形的面积是(x+x+5)2,其中它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,据此易得x=2.那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程x2﹣4x﹣12=0的正确构图是 ② .(只填序号)
【分析】仿造案例,构造面积是(x+x﹣4)2的大正方形,由它的面积为4×12+42,可求出x=6,此题得解.
【解答】解:∵x2﹣4x﹣12=0即x(x﹣4)=12,
∴构造如图②中大正方形的面积是(x+x﹣4)2,其中它又等于四个矩形的面积加上中间小正方形的面积,即4×12+42,
据此易得x=6.
故答案为:②.
8.(2019秋?青岛期中)如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm,且折成的长方体盒子表面积是950cm2,此时长方体盒子的体积为 1500 cm3.
【分析】设剪掉的小正方形的边长为xcm,根据题意列出方程,求出方程的解得到x的值,求出所求即可.
【解答】解:设剪掉的小正方形的边长为xcm,
根据题意,得:2x2+20x×2=30×40﹣950,
x2+20x﹣125=0,
解这个方程得:x1=5,x2=﹣25(不合题意,应舍去),
当x=5时,长方体盒子的体积为:x(30﹣2x)(20﹣x)=5×(30﹣2×5)×(20﹣5)=1500(cm2),
答:此时长方体盒子的体积1500cm3
故答案为:1500.
9.(2019秋?会宁县期中)现要在一个长为40m,宽为26m的矩形花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为864m2,那么小道的宽度应是 2 m.
【分析】设小道进出口的宽度为x米,然后利用其种植花草的面积为864m2列出方程求解即可.
【解答】解:设小道进出口的宽度为x米,依题意得(40﹣2x)(26﹣x)=864,
整理,得x2﹣46x+88=0.
解得,x1=2,x2=44.
∵44>40(不合题意,舍去),
∴x=2.
答:小道进出口的宽度应为2米.
故答案为:2.
10.(2019春?西湖区校级期中)将一条长为56cm的铁丝剪成两段并把每一段铁丝做成一个正方形,使这两个正方形的面积之和等于100cm2,则较小的一个正方形的边长为 6 cm.
【分析】这段铁丝被分成两段后,围成正方形.其中一个正方形的边长为xcm,则另一个正方形的边长为(14﹣x),根据“两个正方形的面积之和等于100cm2”作为相等关系列方程,解方程即可求解;
【解答】解:设其中一个正方形的边长为xcm,则另一个正方形的边长为(14﹣x)cm,
依题意列方程得x2+(14﹣x)2=100,
整理得:x2﹣14x+48=0,
(x﹣6)(x﹣8)=0,
解方程得x1=6,x2=8,
故答案为:6;
三.解答题
11.(2019?徐州)如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?
【分析】设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,宽为(20﹣2x)cm,高为xcm,根据长方体盒子的侧面积为200cm2,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.
【解答】解:设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,宽为(20﹣2x)cm,高为xcm,
依题意,得:2×[(30﹣2x)+(20﹣2x)]x=200,
整理,得:2x2﹣25x+50=0,
解得:x1=,x2=10.
当x=10时,20﹣2x=0,不合题意,舍去.
答:当剪去正方形的边长为cm时,所得长方体盒子的侧面积为200cm2.
12.(2019?襄阳)改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为112m2,则小路的宽应为多少?
【分析】设小路的宽应为xm,那么草坪的总长度和总宽度应该为(16﹣2x),(9﹣x);那么根据题意得出方程,解方程即可.
【解答】解:设小路的宽应为xm,
根据题意得:(16﹣2x)(9﹣x)=112,
解得:x1=1,x2=16.
∵16>9,
∴x=16不符合题意,舍去,
∴x=1.
答:小路的宽应为1m.
13.(2019?南京)某地计划对矩形广场进行扩建改造.如图,原广场长50m,宽40m,要求扩充后的矩形广场长与宽的比为3:2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米100元.如果计划总费用642000元,扩充后广场的长和宽应分别是多少米?
【分析】设扩充后广场的长为3xm,宽为2xm,根据矩形的面积公式和总价=单价×数量列出方程并解答.
【解答】解:设扩充后广场的长为3xm,宽为2xm,
依题意得:3x?2x?100+30(3x?2x﹣50×40)=642000
解得x1=30,x2=﹣30(舍去).
所以3x=90,2x=60,
答:扩充后广场的长为90m,宽为60m.
(时间45分钟 满分100分)
一.选择题(每小题7分,共42分)
1.(2019秋?江津区期中)从正方形的铁皮上,截去2cm宽的一条长方形,余下的面积是48cm2,则原来的正方形铁皮的边长是( )
A.7cm B.8cm C.9cm D.10cm
2.(2019秋?覃塘区期中)若一个直角三角形的两条直角边长之和为14,面积为24,则其斜边的长是( )
A.2 B.4 C.8 D.10
3.(2019秋?锡山区期中)如图,在长20m、宽18m的矩形草坪上,修筑同样宽的三条(横向一条,纵向两条矩形)道路,要使草坪面积达到306m2,则道路宽度是( )
A.27m B.26m C.2m D.1m
4.(2018秋?金凤区校级期中)如图,在一块长为30m,宽为24m的矩形空地上,修建同样宽的两条互相垂直的小路,其余部分建成花园,已知小路的占地面积为53m2,那么小路的宽为多少?( )
A.1m B.1.5m C.2m D.2.5m
5.(2019秋?越秀区校级月考)如图Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,动点P从点A出发沿AB边以1cm/秒的速度向点B匀速移动,同时,点Q从点B出发沿BC边以2cm/秒的速度向点C匀速移动,当P、Q两点中有一个点到达终点时另一个点也停止运动.运动( )秒后,△PBQ面积为5cm2.
A.0.5 B.1 C.5 D.1或5
6.(2018秋?高邮市校级月考)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.若苗圃园的面积为72平方米,则x为( )
A.12 B.10 C.15 D.8
二.填空题(每小题7分,共28分)
7.(2019?宁夏)你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢!以方程x2+5x﹣14=0即x(x+5)=14为例加以说明.数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图)中大正方形的面积是(x+x+5)2,其中它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,据此易得x=2.那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程x2﹣4x﹣12=0的正确构图是 .(只填序号)
8.(2019秋?青岛期中)如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm,且折成的长方体盒子表面积是950cm2,此时长方体盒子的体积为 cm3.
9.(2019秋?会宁县期中)现要在一个长为40m,宽为26m的矩形花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为864m2,那么小道的宽度应是 m.
10.(2019春?西湖区校级期中)将一条长为56cm的铁丝剪成两段并把每一段铁丝做成一个正方形,使这两个正方形的面积之和等于100cm2,则较小的一个正方形的边长为 cm.
三.解答题(共30分)
11.(10分)(2019?徐州)如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?
12.(10分)(2019?襄阳)改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为112m2,则小路的宽应为多少?
13.(10分)(2019?南京)某地计划对矩形广场进行扩建改造.如图,原广场长50m,宽40m,要求扩充后的矩形广场长与宽的比为3:2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米100元.如果计划总费用642000元,扩充后广场的长和宽应分别是多少米?
2.3(2) 一元二次方程的应用测试卷
参考答案与试题解析
一.选择题
1.(2019秋?江津区期中)从正方形的铁皮上,截去2cm宽的一条长方形,余下的面积是48cm2,则原来的正方形铁皮的边长是( )
A.7cm B.8cm C.9cm D.10cm
【分析】设原来的正方形铁皮的边长为xcm,利用余下的面积=正方形的面积﹣剪去长方形的面积,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
【解答】解:设原来的正方形铁皮的边长为xcm,
依题意,得:x2﹣2x=48,
解得:x1=8,x2=﹣6(不合题意,舍去).
故选:B.
2.(2019秋?覃塘区期中)若一个直角三角形的两条直角边长之和为14,面积为24,则其斜边的长是( )
A.2 B.4 C.8 D.10
【分析】设一边长为x,然后表示出另一边,然后利用直角三角形的面积的计算方法列出方程即可;然后再根据勾股定理求得斜边长.
【解答】解:设其中一条直角边的长为x,则另一条直角边为(14﹣x),根据题意得:x(14﹣x)=24,
整理得:x2﹣14x+48=0.
解得x1=6,x2=8,
所以斜边长为:=10.
故选:D.
3.(2019秋?锡山区期中)如图,在长20m、宽18m的矩形草坪上,修筑同样宽的三条(横向一条,纵向两条矩形)道路,要使草坪面积达到306m2,则道路宽度是( )
A.27m B.26m C.2m D.1m
【分析】设道路的宽度为xm,将剩余部分合成矩形,利用矩形的面积公式及草坪面积为306m2,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.
【解答】解:设道路的宽度为xm,
根据题意得:(20﹣2x)(18﹣x)=306,
化简得:x2﹣28x+27=0,
解得:x1=1,x2=27.
∵20﹣2x>0,
∴x<10,
∴x=1.
故选:D.
4.(2018秋?金凤区校级期中)如图,在一块长为30m,宽为24m的矩形空地上,修建同样宽的两条互相垂直的小路,其余部分建成花园,已知小路的占地面积为53m2,那么小路的宽为多少?( )
A.1m B.1.5m C.2m D.2.5m
【分析】把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程求解即可.
【解答】解:设道路的宽应为x米,由题意有
(30﹣x)(24﹣x)=30×24﹣53,
解得:x=53(舍去)或x=1.
答:修建的路宽为1米.
故选:A.
5.(2019秋?越秀区校级月考)如图Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,动点P从点A出发沿AB边以1cm/秒的速度向点B匀速移动,同时,点Q从点B出发沿BC边以2cm/秒的速度向点C匀速移动,当P、Q两点中有一个点到达终点时另一个点也停止运动.运动( )秒后,△PBQ面积为5cm2.
A.0.5 B.1 C.5 D.1或5
【分析】设经过x秒钟,使△PBQ的面积为8cm2,得到BP=6﹣x,BQ=2x,根据三角形的面积公式得出方程×(6﹣x)×2x=5,求出即可.
【解答】解:设经过x秒钟,使△PBQ的面积为5cm2,
BP=6﹣x,BQ=2x,
∵∠B=90°,
∴BP×BQ=5,
∴×(6﹣x)×2x=5,
∴x1=1,x2=5(舍去),
答:如果点P、Q分别从A、B同时出发,经过1秒钟,使△PBQ的面积为5cm2.
故选:B.
6.(2018秋?高邮市校级月考)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.若苗圃园的面积为72平方米,则x为( )
A.12 B.10 C.15 D.8
【分析】根据等量关系列方程求解即可.
【解答】解:根据题意得:x×(30﹣2x)=72
解得:x1=12,x2=3
当x=12时,30﹣2x=6<18
当x=3时,30﹣2x=24>18(不合题意舍去)
故选:A.
二.填空题
7.(2019?宁夏)你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢!以方程x2+5x﹣14=0即x(x+5)=14为例加以说明.数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图)中大正方形的面积是(x+x+5)2,其中它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,据此易得x=2.那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程x2﹣4x﹣12=0的正确构图是 ② .(只填序号)
【分析】仿造案例,构造面积是(x+x﹣4)2的大正方形,由它的面积为4×12+42,可求出x=6,此题得解.
【解答】解:∵x2﹣4x﹣12=0即x(x﹣4)=12,
∴构造如图②中大正方形的面积是(x+x﹣4)2,其中它又等于四个矩形的面积加上中间小正方形的面积,即4×12+42,
据此易得x=6.
故答案为:②.
8.(2019秋?青岛期中)如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm,且折成的长方体盒子表面积是950cm2,此时长方体盒子的体积为 1500 cm3.
【分析】设剪掉的小正方形的边长为xcm,根据题意列出方程,求出方程的解得到x的值,求出所求即可.
【解答】解:设剪掉的小正方形的边长为xcm,
根据题意,得:2x2+20x×2=30×40﹣950,
x2+20x﹣125=0,
解这个方程得:x1=5,x2=﹣25(不合题意,应舍去),
当x=5时,长方体盒子的体积为:x(30﹣2x)(20﹣x)=5×(30﹣2×5)×(20﹣5)=1500(cm2),
答:此时长方体盒子的体积1500cm3
故答案为:1500.
9.(2019秋?会宁县期中)现要在一个长为40m,宽为26m的矩形花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为864m2,那么小道的宽度应是 2 m.
【分析】设小道进出口的宽度为x米,然后利用其种植花草的面积为864m2列出方程求解即可.
【解答】解:设小道进出口的宽度为x米,依题意得(40﹣2x)(26﹣x)=864,
整理,得x2﹣46x+88=0.
解得,x1=2,x2=44.
∵44>40(不合题意,舍去),
∴x=2.
答:小道进出口的宽度应为2米.
故答案为:2.
10.(2019春?西湖区校级期中)将一条长为56cm的铁丝剪成两段并把每一段铁丝做成一个正方形,使这两个正方形的面积之和等于100cm2,则较小的一个正方形的边长为 6 cm.
【分析】这段铁丝被分成两段后,围成正方形.其中一个正方形的边长为xcm,则另一个正方形的边长为(14﹣x),根据“两个正方形的面积之和等于100cm2”作为相等关系列方程,解方程即可求解;
【解答】解:设其中一个正方形的边长为xcm,则另一个正方形的边长为(14﹣x)cm,
依题意列方程得x2+(14﹣x)2=100,
整理得:x2﹣14x+48=0,
(x﹣6)(x﹣8)=0,
解方程得x1=6,x2=8,
故答案为:6;
三.解答题
11.(2019?徐州)如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?
【分析】设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,宽为(20﹣2x)cm,高为xcm,根据长方体盒子的侧面积为200cm2,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.
【解答】解:设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,宽为(20﹣2x)cm,高为xcm,
依题意,得:2×[(30﹣2x)+(20﹣2x)]x=200,
整理,得:2x2﹣25x+50=0,
解得:x1=,x2=10.
当x=10时,20﹣2x=0,不合题意,舍去.
答:当剪去正方形的边长为cm时,所得长方体盒子的侧面积为200cm2.
12.(2019?襄阳)改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为112m2,则小路的宽应为多少?
【分析】设小路的宽应为xm,那么草坪的总长度和总宽度应该为(16﹣2x),(9﹣x);那么根据题意得出方程,解方程即可.
【解答】解:设小路的宽应为xm,
根据题意得:(16﹣2x)(9﹣x)=112,
解得:x1=1,x2=16.
∵16>9,
∴x=16不符合题意,舍去,
∴x=1.
答:小路的宽应为1m.
13.(2019?南京)某地计划对矩形广场进行扩建改造.如图,原广场长50m,宽40m,要求扩充后的矩形广场长与宽的比为3:2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米100元.如果计划总费用642000元,扩充后广场的长和宽应分别是多少米?
【分析】设扩充后广场的长为3xm,宽为2xm,根据矩形的面积公式和总价=单价×数量列出方程并解答.
【解答】解:设扩充后广场的长为3xm,宽为2xm,
依题意得:3x?2x?100+30(3x?2x﹣50×40)=642000
解得x1=30,x2=﹣30(舍去).
所以3x=90,2x=60,
答:扩充后广场的长为90m,宽为60m.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
