3.3 方差和标准差同步测试题（含解析）

3.3 方差和标准差测试卷
（时间45分钟 满分100分）
一．选择题（每小题7分，共42分）
1．（2019?益阳）已知一组数据5，8，8，9，10，以下说法错误的是（　　）
A．平均数是8 B．众数是8 C．中位数是8 D．方差是8
2．（2019?鄂州）已知一组数据为7，2，5，x，8，它们的平均数是5，则这组数据的方差为（　　）
A．3 B．4.5 C．5.2 D．6
3．（2019?锦州）甲、乙、丙、丁四名同学进行跳高测试，每人10次跳高成绩的平均数都是1.28m，方差分别是s甲2＝0.60，s乙2＝0.62，s丙2＝0.58，s丁2＝0.45，则这四名同学跳高成绩最稳定的是（　　）
A．甲 B．乙 C．丙 D．丁
4．（2015春?扬州期中）一组数据1，﹣1，0，﹣1，1的方差和标准差分别是（　　）
A．0，0 B．0.8，0.64 C．1，1 D．0.8，
5．（2019?杭州）点点同学对数据26，36，46，5□，52进行统计分析，发现其中一个两位数的个位数字被黑水涂污看不到了，则计算结果与被涂污数字无关的是（　　）
A．平均数 B．中位数 C．方差 D．标准差
6．（2017春?婺城区校级期中）已知数据1、5、4、3、3、2，则下列关于这组数据的说法错误的是（　　）
A．平均数和众数都是3 B．中位数为3
C．方差为10 D．标准差是
二．填空题（每小题7分，共28分）
7．（2019?铜仁市）小刘和小李参加射击训练，各射击10次的平均成绩相同，如果他们射击成绩的方差分别是S小刘2＝0.6，S小李2＝1.4，那么两人中射击成绩比较稳定的是　 　；
8．（2019?柳州）已知一组数据共有5个数，它们的方差是0.4，众数、中位数和平均数都是8，最大的数是9，则最小的数是　 　．
9．（2019秋?龙口市期中）已知一个样本3，x，4，6，7，它们的平均数是5，则这个样本的标准差是　 　．
10．（2014秋?烟台期中）一组数据a，b，c的方差是9，则数据a+1，b+1，c+1的标准差为　 　．
三．解答题（共30分）
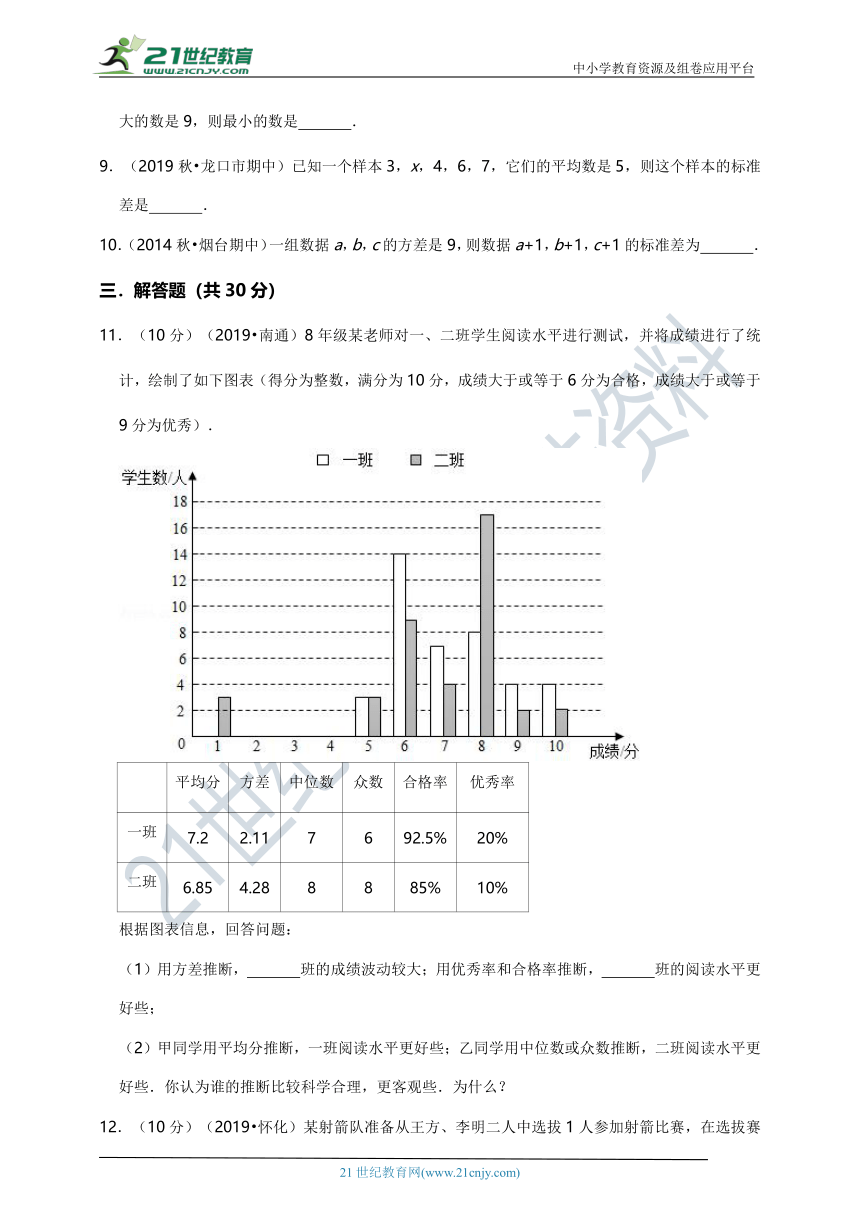
11．（10分）（2019?南通）8年级某老师对一、二班学生阅读水平进行测试，并将成绩进行了统计，绘制了如下图表（得分为整数，满分为10分，成绩大于或等于6分为合格，成绩大于或等于9分为优秀）．
平均分
方差
中位数
众数
合格率
优秀率
一班
7.2
2.11
7
6
92.5%
20%
二班
6.85
4.28
8
8
85%
10%
根据图表信息，回答问题：
（1）用方差推断，　 　班的成绩波动较大；用优秀率和合格率推断，　 　班的阅读水平更好些；
（2）甲同学用平均分推断，一班阅读水平更好些；乙同学用中位数或众数推断，二班阅读水平更好些．你认为谁的推断比较科学合理，更客观些．为什么？
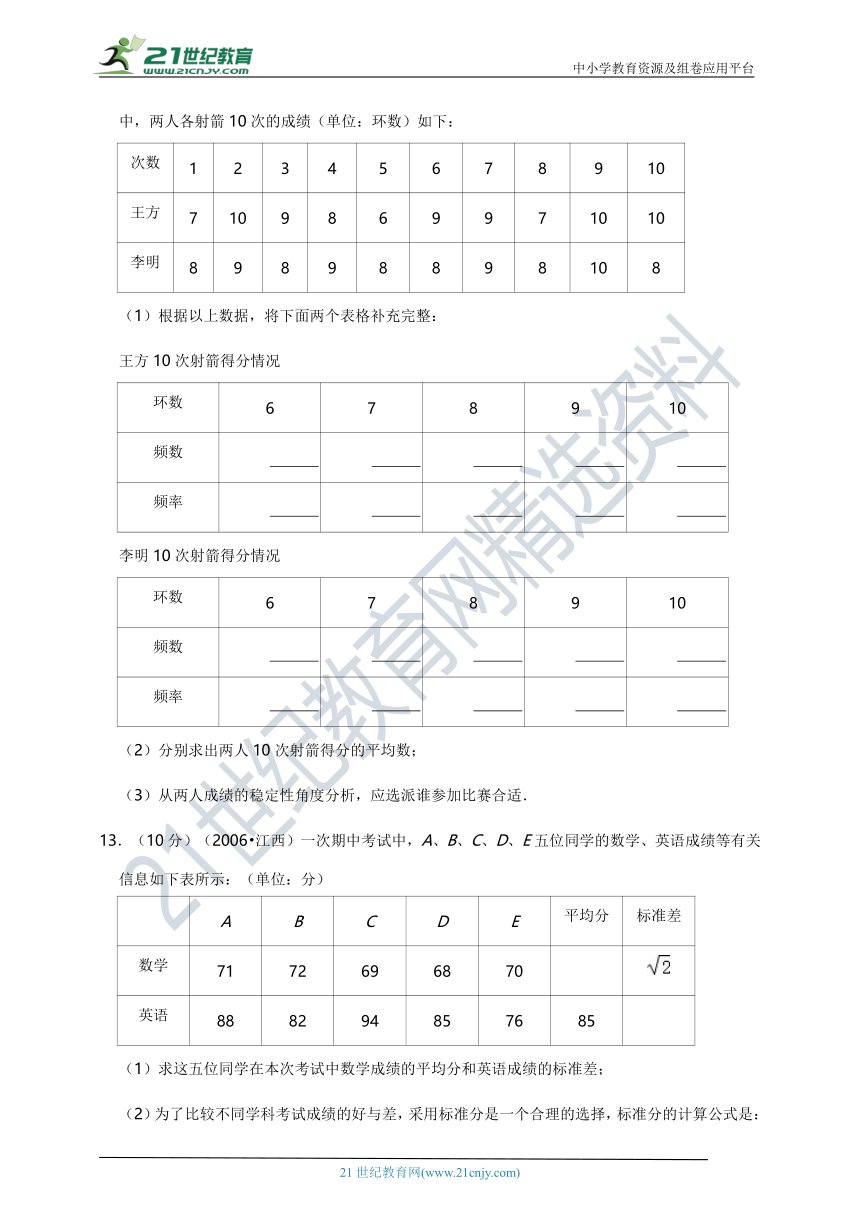
12．（10分）（2019?怀化）某射箭队准备从王方、李明二人中选拔1人参加射箭比赛，在选拔赛中，两人各射箭10次的成绩（单位：环数）如下：
次数
1
2
3
4
5
6
7
8
9
10
王方
7
10
9
8
6
9
9
7
10
10
李明
8
9
8
9
8
8
9
8
10
8
（1）根据以上数据，将下面两个表格补充完整：
王方10次射箭得分情况
环数
6
7
8
9
10
频数
　 　
　 　
　 　
　 　
　 　
频率
　 　
　 　
　 　
　 　
　 　
李明10次射箭得分情况
环数
6
7
8
9
10
频数
　 　
　 　
　 　
　 　
　 　
频率
　 　
　 　
　 　
　 　
　 　
（2）分别求出两人10次射箭得分的平均数；
（3）从两人成绩的稳定性角度分析，应选派谁参加比赛合适．
13．（10分）（2006?江西）一次期中考试中，A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示：（单位：分）
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70
英语
88
82
94
85
76
85
（1）求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差；
（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，标准分的计算公式是：标准分＝（个人成绩一平均成绩）÷成绩标准差．
从标准分看，标准分大的考试成绩更好．请问A同学在本次考试中，数学与英语哪个学科考得更好？
友情提示：一组数据的标准差计算公式是S＝，其中为n个数据x1，x2，…xnr的平均数．

3.3 方差和标准差测试卷
参考答案与试题解析
一．选择题
1．（2019?益阳）已知一组数据5，8，8，9，10，以下说法错误的是（　　）
A．平均数是8 B．众数是8 C．中位数是8 D．方差是8
【分析】分别计算平均数，众数，中位数，方差后判断．
【解答】解：由平均数的公式得平均数＝（5+8+8+9+10）÷5＝8，
方差＝[（5﹣8）2+（8﹣8）2+（8﹣8）2+（9﹣8）2+（10﹣8）2]＝2.8，
将5个数按从小到大的顺序排列为：5，8，8，9，10，第3个数为8，即中位数为8，
5个数中8出现了两次，次数最多，即众数为8，
故选：D．
2．（2019?鄂州）已知一组数据为7，2，5，x，8，它们的平均数是5，则这组数据的方差为（　　）
A．3 B．4.5 C．5.2 D．6
【分析】先由平均数是5计算x的值，再根据方差的计算公式，直接计算可得．
【解答】解：∵一组数据7，2，5，x，8的平均数是5，
∴5＝（7+2+5+x+8），
∴x＝5×5﹣7﹣2﹣5﹣8＝3，
∴s2＝[（7﹣5）2+（2﹣5）2+（5﹣5）2+（3﹣5）2+（8﹣5）2]＝5.2，
故选：C．
3．（2019?锦州）甲、乙、丙、丁四名同学进行跳高测试，每人10次跳高成绩的平均数都是1.28m，方差分别是s甲2＝0.60，s乙2＝0.62，s丙2＝0.58，s丁2＝0.45，则这四名同学跳高成绩最稳定的是（　　）
A．甲 B．乙 C．丙 D．丁
【分析】直接利用方差是反映一组数据的波动大小的一个量，方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好，进而分析即可．
【解答】解：∵s甲2＝0.60，s乙2＝0.62，s丙2＝0.58，s丁2＝0.45，
∴s丁2＜s丙2＜s甲2＜s乙2，
∴成绩最稳定的是丁．
故选：D．
4．（2015春?扬州期中）一组数据1，﹣1，0，﹣1，1的方差和标准差分别是（　　）
A．0，0 B．0.8，0.64 C．1，1 D．0.8，
【分析】要求标准差，首先求出平均数，用方差公式求出方差，再开平方即可．
【解答】解：（﹣1+1+0﹣1+1）＝0，
方差S2＝[（1﹣0）2+（﹣1﹣0）2+（0﹣0）2+（﹣1﹣0）2+（1﹣0）2]
＝[12+（﹣1）2+02+（﹣1）2+12]
＝
故标准差是S＝＝．
故选：D．
5．（2019?杭州）点点同学对数据26，36，46，5□，52进行统计分析，发现其中一个两位数的个位数字被黑水涂污看不到了，则计算结果与被涂污数字无关的是（　　）
A．平均数 B．中位数 C．方差 D．标准差
【分析】利用平均数、中位数、方差和标准差的定义对各选项进行判断．
【解答】解：这组数据的平均数、方差和标准差都与第4个数有关，而这组数据的中位数为46，与第4个数无关．
故选：B．
6．（2017春?婺城区校级期中）已知数据1、5、4、3、3、2，则下列关于这组数据的说法错误的是（　　）
A．平均数和众数都是3 B．中位数为3
C．方差为10 D．标准差是
【分析】根据平均数、中位数和众数、方差、标准差的计算公式分别进行计算即可得出答案．
【解答】解：根据平均数、中位数和众数的定义可得，平均数、中位数和众数都是3；
方差为S2＝[（1﹣3）2+（2﹣3）2+（3﹣3）2+（3﹣3）2+（4﹣3）2+（5﹣3）2]＝，
标准差是S＝＝．
则这组数据的说法错误的是C；
故选：C．
二．填空题
7．（2019?铜仁市）小刘和小李参加射击训练，各射击10次的平均成绩相同，如果他们射击成绩的方差分别是S小刘2＝0.6，S小李2＝1.4，那么两人中射击成绩比较稳定的是　小刘　；
【分析】根据方差的意义即可求出答案．
【解答】解：由于S小刘2＜S小李2，且两人10次射击成绩的平均值相等，
∴两人中射击成绩比较稳定的是小刘，
故答案为：小刘
8．（2019?柳州）已知一组数据共有5个数，它们的方差是0.4，众数、中位数和平均数都是8，最大的数是9，则最小的数是　7　．
【分析】根据5个数的平均数是8，可知这5个数的和为40，根据5个数的中位数是8，得出中间的数是8，根据众数是8，得出至少有2个8，再根据5个数的和减去2个8和1个9得出前面2个数的和为15，再根据方差得出前面的2个数为7和8，即可得出结果．
【解答】解：∵5个数的平均数是8，
∴这5个数的和为40，
∵5个数的中位数是8，
∴中间的数是8，
∵众数是8，
∴至少有2个8，
∵40﹣8﹣8﹣9＝15，
由方差是0.4得：前面的2个数为7和8，
∴最小的数是7；
故答案为：7..
9．（2019秋?龙口市期中）已知一个样本3，x，4，6，7，它们的平均数是5，则这个样本的标准差是　　．
【分析】根据平均数的计算公式先计算出x的值，再根据方差的公式计算出方差，然后计算出标准差即可．
【解答】解：∵样本3，x，4，6，7，它们的平均数是5，
∴x＝25﹣3﹣4﹣6﹣7＝5
∴S2＝[（3﹣5）2+（5﹣5）2+（4﹣5）2+（6﹣5）2+（7﹣5）2]＝2，
∴标准差＝；
故答案为：．
10．（2014秋?烟台期中）一组数据a，b，c的方差是9，则数据a+1，b+1，c+1的标准差为　3　．
【分析】首先根据a，b，c的方差是9求得数据a+1，b+1，c+1的方差，然后开方即可求得标准差．
【解答】解：∵a，b，c的方差是9，
∴数据a+1，b+1，c+1的方差为9，
∴标准差为3，
故答案为：3．
三．解答题
11．（2019?南通）8年级某老师对一、二班学生阅读水平进行测试，并将成绩进行了统计，绘制了如下图表（得分为整数，满分为10分，成绩大于或等于6分为合格，成绩大于或等于9分为优秀）．
平均分
方差
中位数
众数
合格率
优秀率
一班
7.2
2.11
7
6
92.5%
20%
二班
6.85
4.28
8
8
85%
10%
根据图表信息，回答问题：
（1）用方差推断，　二　班的成绩波动较大；用优秀率和合格率推断，　一　班的阅读水平更好些；
（2）甲同学用平均分推断，一班阅读水平更好些；乙同学用中位数或众数推断，二班阅读水平更好些．你认为谁的推断比较科学合理，更客观些．为什么？
【分析】（1）从方差上看，二班的方差较大，二班波动较大，合格率、优秀率一班都比二班高，
（2）平均分会受极端值的影响，众数、中位数则是反映一组数据的集中趋势和平均水平，因此用众数、中位数进行分析比较客观．
【解答】解：（1）从方差看，二班成绩波动较大，从众数、中位数上看，一班的成绩较好，
故答案为：二，一．
（2）乙同学的说法较合理，众数和中位数是反映一组数据集中发展趋势和集中水平，由于二班的众数、中位数都比一班的要好．
12．（2019?怀化）某射箭队准备从王方、李明二人中选拔1人参加射箭比赛，在选拔赛中，两人各射箭10次的成绩（单位：环数）如下：
次数
1
2
3
4
5
6
7
8
9
10
王方
7
10
9
8
6
9
9
7
10
10
李明
8
9
8
9
8
8
9
8
10
8
（1）根据以上数据，将下面两个表格补充完整：
王方10次射箭得分情况
环数
6
7
8
9
10
频数
　1　
　2　
　1　
　3　
　3　
频率
　0.1　
　0.2　
　0.1　
　0.3　
　0.3　
李明10次射箭得分情况
环数
6
7
8
9
10
频数
　0　
　0　
　6　
　3　
　1　
频率
　0　
　0　
　0.6　
　0.3　
　0.1　
（2）分别求出两人10次射箭得分的平均数；
（3）从两人成绩的稳定性角度分析，应选派谁参加比赛合适．
【分析】（1）根据各组的频数除以10即可得到结论；
（2）根据加权平均数的定义即可得到结论；
（3）根据方差公式即可得到结论．
【解答】解：（1）
环数
6
7
8
9
10
频数
1
2
1
3
3
频率
0.1
0.2
0.1
0.3
0.3
李明10次射箭得分情况
环数
6
7
8
9
10
频数
0
0
6
3
1
频率
0
0
0.6
0.3
0.1
（2）王方的平均数＝（6+14+8+27+30）＝8.5；李明的平均数＝（48+27+10）＝8.5；
（3）∵S＝[（6﹣8.5）2+2（7﹣8.5）2+（8﹣8.5）2+3（9﹣8.5）2+3（10﹣8.5）2]＝1.85；
S＝[6（8﹣8.5）2+3（9﹣8.5）2+（10﹣8.5）2＝0.45；
∵S＞S，
∴应选派李明参加比赛合适．
13．（2006?江西）一次期中考试中，A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示：（单位：分）
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70
英语
88
82
94
85
76
85
（1）求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差；
（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，标准分的计算公式是：标准分＝（个人成绩一平均成绩）÷成绩标准差．
从标准分看，标准分大的考试成绩更好．请问A同学在本次考试中，数学与英语哪个学科考得更好？
友情提示：一组数据的标准差计算公式是S＝，其中为n个数据x1，x2，…xnr的平均数．
【分析】根据平均数和标准差的概念求解．数学考试成绩的平均分70；英语考试成绩的标准差S英语＝6；设A同学数学考试成绩标准分为P数学，英语考试成绩标准分为P英语，则P数学＝（71﹣70）+＝﹣；P英语＝（88﹣85）÷6＝；然后根据标准差的意义得出结论．
【解答】解：（1）数学考试成绩的平均分数学＝（71+72+69+68+70）＝70，
英语考试成绩的标准差S英语＝＝6，
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70
70

英语
88
82
94
85
76
85
6
（2）设A同学数学考试成绩标准分为P数学，英语考试成绩标准分为P英语，
则P数学＝（71﹣70）÷＝；
P英语＝（88﹣85）÷6＝；
∵P数学＞P英语，
∴从标准分来看，A同学数学比英语考得更好．