浙教版八年级数学下册第4章 平行四边形单元测试题(PDF版 含答案)
文档属性
| 名称 | 浙教版八年级数学下册第4章 平行四边形单元测试题(PDF版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 238.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-28 00:00:00 | ||
图片预览



文档简介
第 4章 平行四边形
一、选择题(每小题 5分,共 30分)
1.已知?ABCD中相邻两个内角的度数之比为 2∶3,则此四边形中较大内角的度数为 ( )
A.72° B.90° C.108° D.126°
2在平面直角坐标系中,?ABCD的顶点 A,B,C的坐标分别是(0,0),(3,0),(4,2),则顶点 D的坐标为
( )
A.(7,2) B.(5,4) C.(1,2) D.(2,1)
3.如图 3,在△ABC中,D,E分别是 BC,AC的中点,BF平分∠ABC,交 DE于点 F,AB=8,BC=6,则
EF的长为 ( )
图 3
A.1 B.2 C.3 D.4
4.在 4×4的正方形网格中每个小正方形的边长均为 1,每个小正方形的顶点叫格点,点 A,B(均在
格点上)的位置如图 4,若以 A,B为顶点画面积为 2 的格点平行四边形,则符合条件的平行四边
形的个数是 ( )
图 4
A.6 B.7 C.9 D.11
5.如图 5,在△ABC中,延长 BC至点 D,使得 CD= BC,过 AC的中点 E作 EF∥CD(点 F位于点
E右侧),且 EF=2CD,连结 DF.若 AB=8,则 DF的长为 ( )
图 5
A.3 B.4 C.2 D.3
6.如图 4,?ABCD 的对角线 AC,BD 相交于点 O,且 AC+BD=16,CD=6,则△ABO 的周长是
( )
图 4
A.10 B.14 C.20 D.22
二、填空题(每小题 5分,共 25分)
7.已知一个多边形的每一个外角都等于 72°,则这个多边形的边数是 .
8.如图 5,?ABCD 中 ,E 是 BA 延长线上一点 ,AB=AE,连结 CE 交 AD 于点 F.若 CF 平分∠
BCD,AB=3,则 BC的长为 .
图 5
9.如图 6,在?ABCD中,AD=5 cm,AB⊥BD,O是两条对角线的交点,OD=2 cm,则 AB=
cm.
图 6
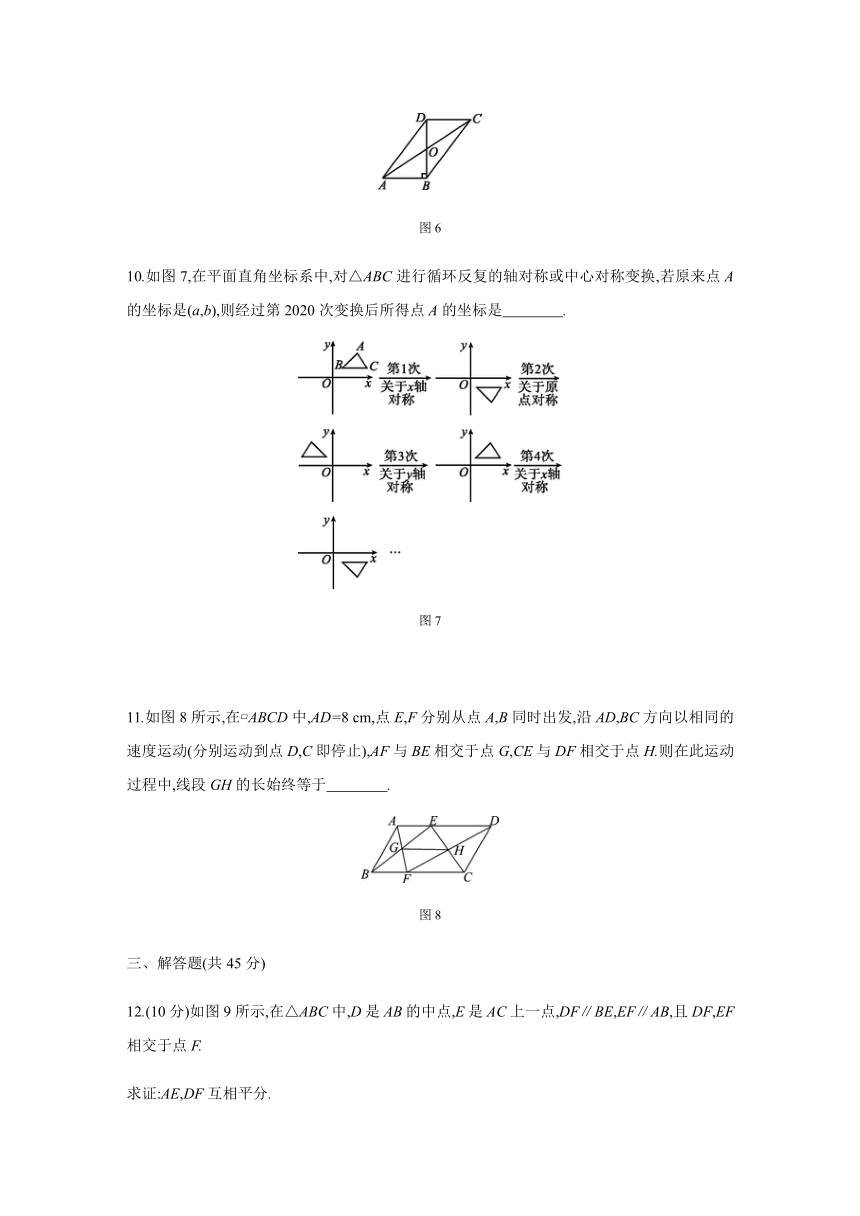
10.如图 7,在平面直角坐标系中,对△ABC进行循环反复的轴对称或中心对称变换,若原来点 A
的坐标是(a,b),则经过第 2020次变换后所得点 A的坐标是 .
图 7
11.如图 8所示,在?ABCD中,AD=8 cm,点 E,F分别从点 A,B同时出发,沿 AD,BC方向以相同的
速度运动(分别运动到点 D,C即停止),AF与 BE相交于点 G,CE与 DF相交于点 H.则在此运动
过程中,线段 GH的长始终等于 .
图 8
三、解答题(共 45分)
12.(10分)如图 9所示,在△ABC中,D是 AB的中点,E是 AC上一点,DF∥BE,EF∥AB,且 DF,EF
相交于点 F.
求证:AE,DF互相平分.
图 9
13.(10分)如图 10,C是 AB的中点,AD=CE,CD=BE.
(1)求证:△ACD≌△CBE;
(2)连结 DE,求证:四边形 CBED是平行四边形.
图 10
14.(12分)如图 11,在平行四边形 ABCD中,E,F分别是 BC,AD的中点.
(1)求证:△ABE≌△CDF;
(2)若 AE=CE,BC=2AB,BC=6,求四边形 AECF的面积.
图 11
15.(13分)如图 12,在△ABC中,D是 BC的中点,点 E在△ABC内,AE平分∠BAC,CE⊥AE,点 F
在 AB上,EF∥BC.
(1)求证:四边形 BDEF是平行四边形;
(2)线段 BF,AB,AC之间具有怎样的数量关系?证明你所得到的结论.
图 12
答案
1.C 2.C 3.A 4.D 5.B 6.B
7.5 8.6
9.3
10.(a,-b)
11.4 cm
12.证明:∵DF∥BE,EF∥BD,
∴四边形 BDFE是平行四边形,
∴EF=BD.
∵D是 AB的中点,
∴AD=BD,∴EF=AD.
又∵EF∥AD,
∴四边形 ADEF是平行四边形,
∴AE,DF互相平分.
13.证明:(1)∵C是 AB的中点,
∴AC=CB.
在△ACD与△CBE中,
∴△ACD≌△CBE.
(2)∵△ACD≌△CBE,
∴∠ACD=∠CBE,
∴CD∥BE.
又∵CD=BE.
∴四边形 CBED是平行四边形.
14.解:(1)证明:∵四边形 ABCD是平行四边形,
∴AB=CD,BC=AD,∠B=∠D.
∵E,F分别是 BC,AD的中点,
∴BE= BC,DF= AD,
∴BE=DF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
(2)过点 A作 AH⊥BC于点 H.
∵BC=2AB=6,E为 BC的中点,F为 AD的中点,
∴AB=BE=CE=AF=DF=3.
又∵AF∥CE,
∴四边形 AECF是平行四边形.
∵AE=EC,
∴AE=AB=BE=CE=3,
∴△ABE是等边三角形,
∴BH= ,
∴AH= = ,
∴S 四边形 AECF=CE×AH=3× = .
15.解:(1)证明:延长 CE交 AB于点 G.
∵AE⊥CE,
∴∠AEG=∠AEC=90°.
又∵∠GAE=∠CAE,AE=AE,
∴△AGE≌△ACE,∴GE=CE.
又∵D是 BC的中点,
∴DE是△BCG的中位线,
∴DE∥BG,即 DE∥BF.
∵EF∥BC,即 EF∥BD,
∴四边形 BDEF是平行四边形.
(2)BF= (AB-AC).
证明:∵四边形 BDEF是平行四边形,∴BF=DE.
∵D,E分别是 BC,GC的中点,
∴BF=DE= BG.
∵△AGE≌△ACE,∴AG=AC,
∴BF= (AB-AG)= (AB-AC).
一、选择题(每小题 5分,共 30分)
1.已知?ABCD中相邻两个内角的度数之比为 2∶3,则此四边形中较大内角的度数为 ( )
A.72° B.90° C.108° D.126°
2在平面直角坐标系中,?ABCD的顶点 A,B,C的坐标分别是(0,0),(3,0),(4,2),则顶点 D的坐标为
( )
A.(7,2) B.(5,4) C.(1,2) D.(2,1)
3.如图 3,在△ABC中,D,E分别是 BC,AC的中点,BF平分∠ABC,交 DE于点 F,AB=8,BC=6,则
EF的长为 ( )
图 3
A.1 B.2 C.3 D.4
4.在 4×4的正方形网格中每个小正方形的边长均为 1,每个小正方形的顶点叫格点,点 A,B(均在
格点上)的位置如图 4,若以 A,B为顶点画面积为 2 的格点平行四边形,则符合条件的平行四边
形的个数是 ( )
图 4
A.6 B.7 C.9 D.11
5.如图 5,在△ABC中,延长 BC至点 D,使得 CD= BC,过 AC的中点 E作 EF∥CD(点 F位于点
E右侧),且 EF=2CD,连结 DF.若 AB=8,则 DF的长为 ( )
图 5
A.3 B.4 C.2 D.3
6.如图 4,?ABCD 的对角线 AC,BD 相交于点 O,且 AC+BD=16,CD=6,则△ABO 的周长是
( )
图 4
A.10 B.14 C.20 D.22
二、填空题(每小题 5分,共 25分)
7.已知一个多边形的每一个外角都等于 72°,则这个多边形的边数是 .
8.如图 5,?ABCD 中 ,E 是 BA 延长线上一点 ,AB=AE,连结 CE 交 AD 于点 F.若 CF 平分∠
BCD,AB=3,则 BC的长为 .
图 5
9.如图 6,在?ABCD中,AD=5 cm,AB⊥BD,O是两条对角线的交点,OD=2 cm,则 AB=
cm.
图 6
10.如图 7,在平面直角坐标系中,对△ABC进行循环反复的轴对称或中心对称变换,若原来点 A
的坐标是(a,b),则经过第 2020次变换后所得点 A的坐标是 .
图 7
11.如图 8所示,在?ABCD中,AD=8 cm,点 E,F分别从点 A,B同时出发,沿 AD,BC方向以相同的
速度运动(分别运动到点 D,C即停止),AF与 BE相交于点 G,CE与 DF相交于点 H.则在此运动
过程中,线段 GH的长始终等于 .
图 8
三、解答题(共 45分)
12.(10分)如图 9所示,在△ABC中,D是 AB的中点,E是 AC上一点,DF∥BE,EF∥AB,且 DF,EF
相交于点 F.
求证:AE,DF互相平分.
图 9
13.(10分)如图 10,C是 AB的中点,AD=CE,CD=BE.
(1)求证:△ACD≌△CBE;
(2)连结 DE,求证:四边形 CBED是平行四边形.
图 10
14.(12分)如图 11,在平行四边形 ABCD中,E,F分别是 BC,AD的中点.
(1)求证:△ABE≌△CDF;
(2)若 AE=CE,BC=2AB,BC=6,求四边形 AECF的面积.
图 11
15.(13分)如图 12,在△ABC中,D是 BC的中点,点 E在△ABC内,AE平分∠BAC,CE⊥AE,点 F
在 AB上,EF∥BC.
(1)求证:四边形 BDEF是平行四边形;
(2)线段 BF,AB,AC之间具有怎样的数量关系?证明你所得到的结论.
图 12
答案
1.C 2.C 3.A 4.D 5.B 6.B
7.5 8.6
9.3
10.(a,-b)
11.4 cm
12.证明:∵DF∥BE,EF∥BD,
∴四边形 BDFE是平行四边形,
∴EF=BD.
∵D是 AB的中点,
∴AD=BD,∴EF=AD.
又∵EF∥AD,
∴四边形 ADEF是平行四边形,
∴AE,DF互相平分.
13.证明:(1)∵C是 AB的中点,
∴AC=CB.
在△ACD与△CBE中,
∴△ACD≌△CBE.
(2)∵△ACD≌△CBE,
∴∠ACD=∠CBE,
∴CD∥BE.
又∵CD=BE.
∴四边形 CBED是平行四边形.
14.解:(1)证明:∵四边形 ABCD是平行四边形,
∴AB=CD,BC=AD,∠B=∠D.
∵E,F分别是 BC,AD的中点,
∴BE= BC,DF= AD,
∴BE=DF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
(2)过点 A作 AH⊥BC于点 H.
∵BC=2AB=6,E为 BC的中点,F为 AD的中点,
∴AB=BE=CE=AF=DF=3.
又∵AF∥CE,
∴四边形 AECF是平行四边形.
∵AE=EC,
∴AE=AB=BE=CE=3,
∴△ABE是等边三角形,
∴BH= ,
∴AH= = ,
∴S 四边形 AECF=CE×AH=3× = .
15.解:(1)证明:延长 CE交 AB于点 G.
∵AE⊥CE,
∴∠AEG=∠AEC=90°.
又∵∠GAE=∠CAE,AE=AE,
∴△AGE≌△ACE,∴GE=CE.
又∵D是 BC的中点,
∴DE是△BCG的中位线,
∴DE∥BG,即 DE∥BF.
∵EF∥BC,即 EF∥BD,
∴四边形 BDEF是平行四边形.
(2)BF= (AB-AC).
证明:∵四边形 BDEF是平行四边形,∴BF=DE.
∵D,E分别是 BC,GC的中点,
∴BF=DE= BG.
∵△AGE≌△ACE,∴AG=AC,
∴BF= (AB-AG)= (AB-AC).
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
