第五章 特殊平行四边形尖子生单元测试题(含答案)
文档属性
| 名称 | 第五章 特殊平行四边形尖子生单元测试题(含答案) | 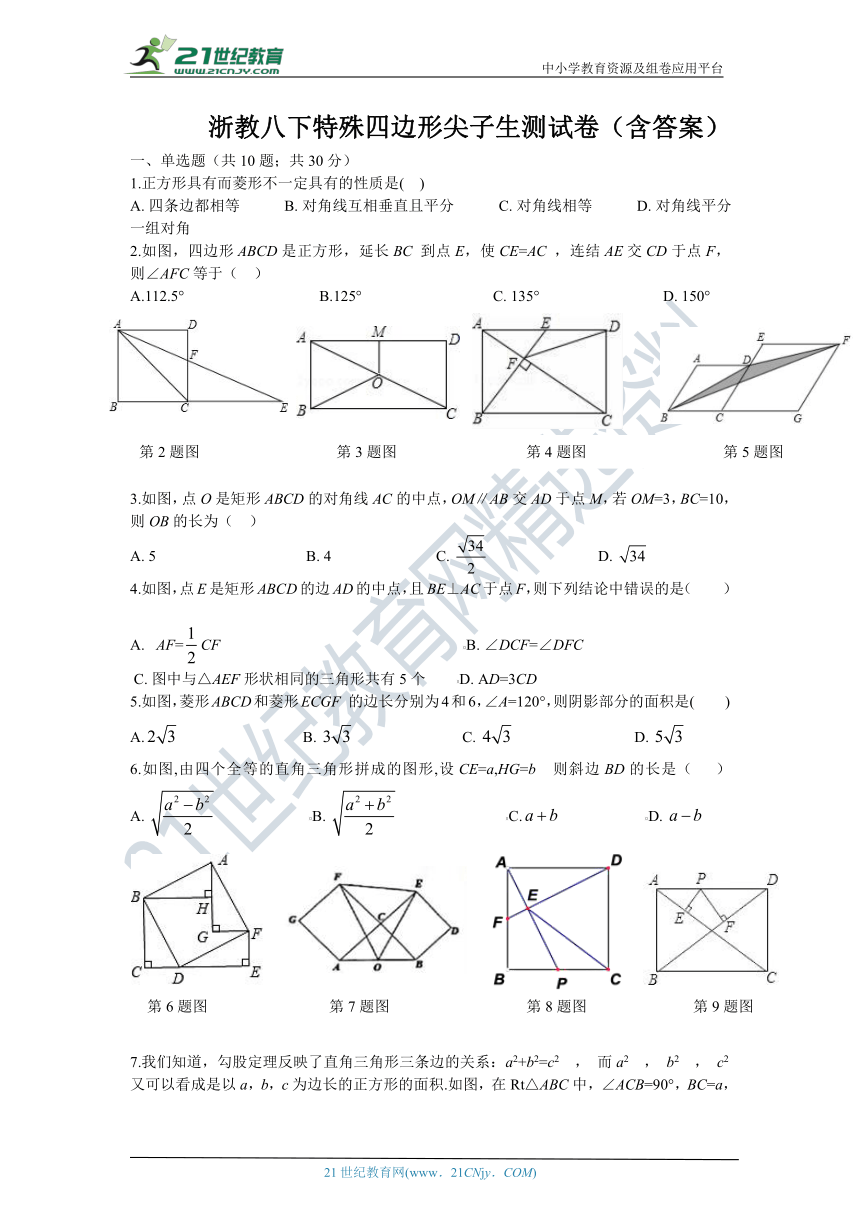 | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 09:04:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教八下特殊四边形尖子生测试卷(含答案)
一、单选题(共10题;共30分)
1.正方形具有而菱形不一定具有的性质是(?? )
A.?四条边都相等???????????B.?对角线互相垂直且平分???????????C.?对角线相等???????????D.?对角线平分一组对角
2.如图,四边形ABCD是正方形,延长BC 到点E,使CE=AC ,连结AE交CD于点F,则∠AFC等于(?? )
A.112.5°???????????????????????????????????B.125°??????????????????????????????????C.?135°????????????????????????????????D.?150°
3.如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( ??)
A.?5???????????????????????????????????????B.?4???????????????????????????C.?????????????????????????????D.?
4.如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( )
?AF=CF??????? ?B.?∠DCF=∠DFC????
?C.?图中与△AEF形状相同的三角形共有5个????????D.?AD=3CD
5.如图,菱形ABCD和菱形ECGF 的边长分别为4和6,∠A=120°,则阴影部分的面积是(? ?????)
A.????????????????????????????????B.?????????????????????????????C.????????????????????????????????D.?
6.如图,由四个全等的直角三角形拼成的图形,设CE=a,HG=b 则斜边BD的长是(??? ) A.?????????????????????????B.?????????????????????????????C.??????????????????????D.?
7.我们知道,勾股定理反映了直角三角形三条边的关系:a2+b2=c2 , 而a2 , b2 , c2又可以看成是以a,b,c为边长的正方形的面积.如图,在Rt△ABC中,∠ACB=90°,BC=a,AC=b,O为AB的中点,分别以AC,BC为边向△ABC外作正方形ACFG,BCED,连结OF,EF,OE,则△OEF的面积为(??? )
A.?????????????????????B.????????????????????C.?????????????????????????D.?
8.如图,正方形ABCD 中,点P,F分别是边BC,AB的中点,连接 AP 、DF 交于点E ,则下列结论错误的是(? ?)
?
A.?AP=DF?????????????????????B.AP┴DF?????????????????????C.?CE=CD?????????????????????D.?CE=EP+EF
9.在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为(??? )
A.???????????????????????????????????????????B.?2??????????????????????????????????????????C.??????????????????????????????????????D.?1
10.将矩形OABC如图放置,O为原点.若点A(﹣1,2),
点B的纵坐标是,则点C的坐标是( ??)
?(4,2)??????????????????????? ?B.?(2,4)????????????????????
??C.???????????????????? ?????D.?
二、填空题(共8题,共24分)
11.在菱形ABCD中,对角线AC=6,BD=8,则菱形ABCD的面积为________.
12.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,连结CE,则∠BCE的度数是________度.
13.如图,四边形ABCD的两条对角线AC,BD互相垂直,A B.CD,是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形的面积为________.
14.如图,直线AB的解析式,交x轴于点A,交y轴于点B,点P为线段AB上一个动点,作PE⊥x轴于点E,PF⊥y轴于点F,则线段EF的最短长度为________.
15.如图,在平面直角坐标系中,长方形ABCO的边COOA分别在x轴,y轴上,点E在边BC上,将该长方形沿AE折叠,点B恰好落在边OC上的点F处,若OA=8,CF=4,则AE所在直线的表达式为________.
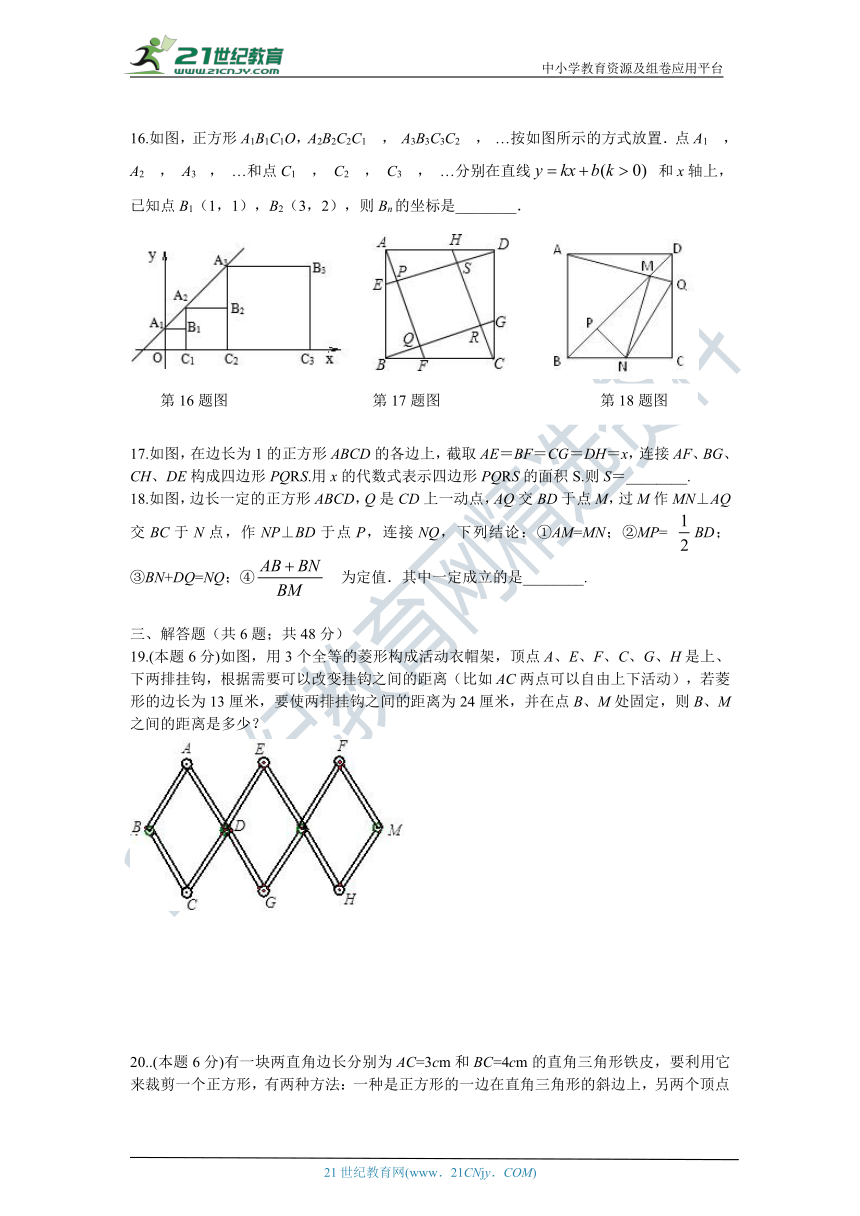
16.如图,正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图所示的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3 , …分别在直线 和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是________.
17.如图,在边长为1的正方形ABCD的各边上,截取AE=BF=CG=DH=x,连接AF、BG、CH、DE构成四边形PQRS.用x的代数式表示四边形PQRS的面积S.则S=________.
18.如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP= BD;③BN+DQ=NQ;④ 为定值.其中一定成立的是________.
三、解答题(共6题;共48分)
19.(本题6分)如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?
20..(本题6分)有一块两直角边长分别为AC=3cm和BC=4cm的直角三角形铁皮,要利用它来裁剪一个正方形,有两种方法:一种是正方形的一边在直角三角形的斜边上,另两个顶点在两条直角边上,如图(1);另一种是一组邻边在直角三角形的两直角边上,另一个顶点在斜边上,如图(2).用计算说明两种情形下正方形的面积哪个大?
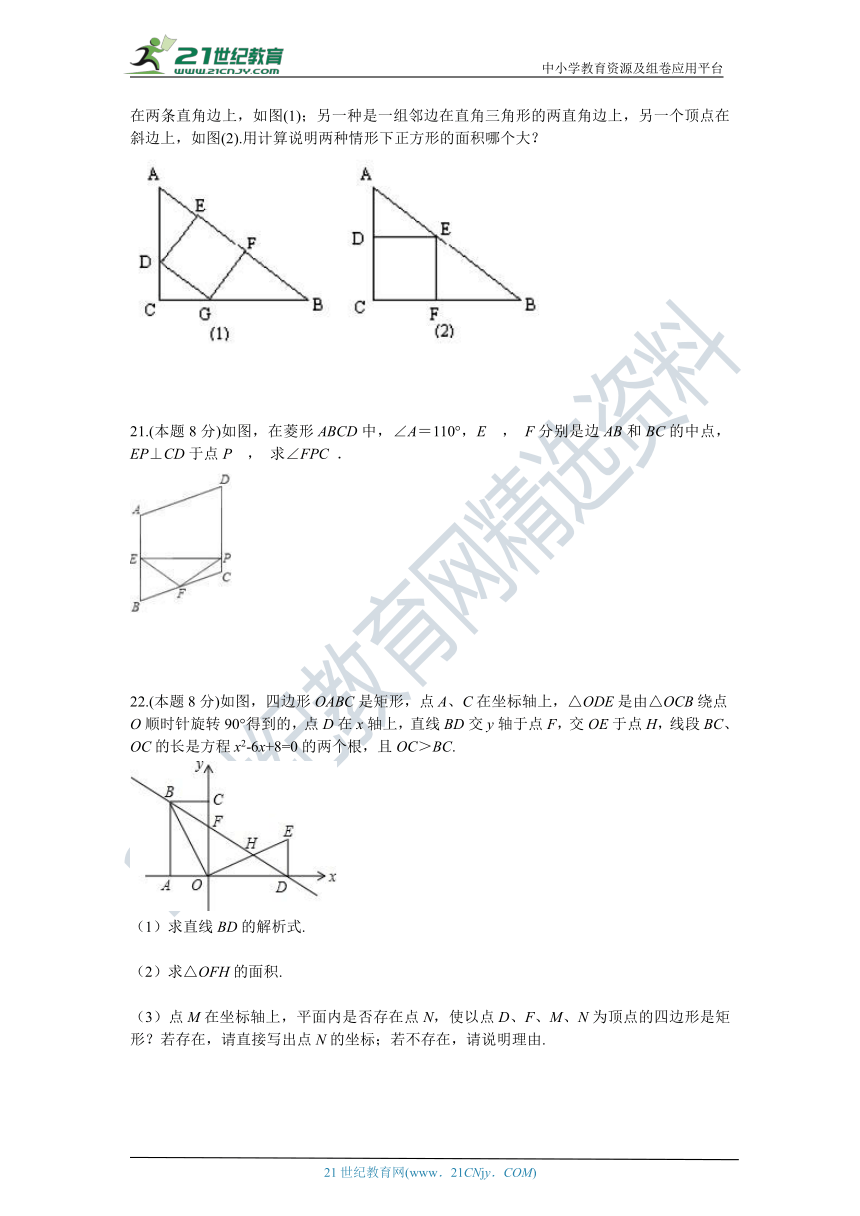
21.(本题8分)如图,在菱形ABCD中,∠A=110°,E , F分别是边AB和BC的中点,EP⊥CD于点P , 求∠FPC .
22.(本题8分)如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC的长是方程x2-6x+8=0的两个根,且OC>BC.
(1)求直线BD的解析式.
(2)求△OFH的面积.
(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
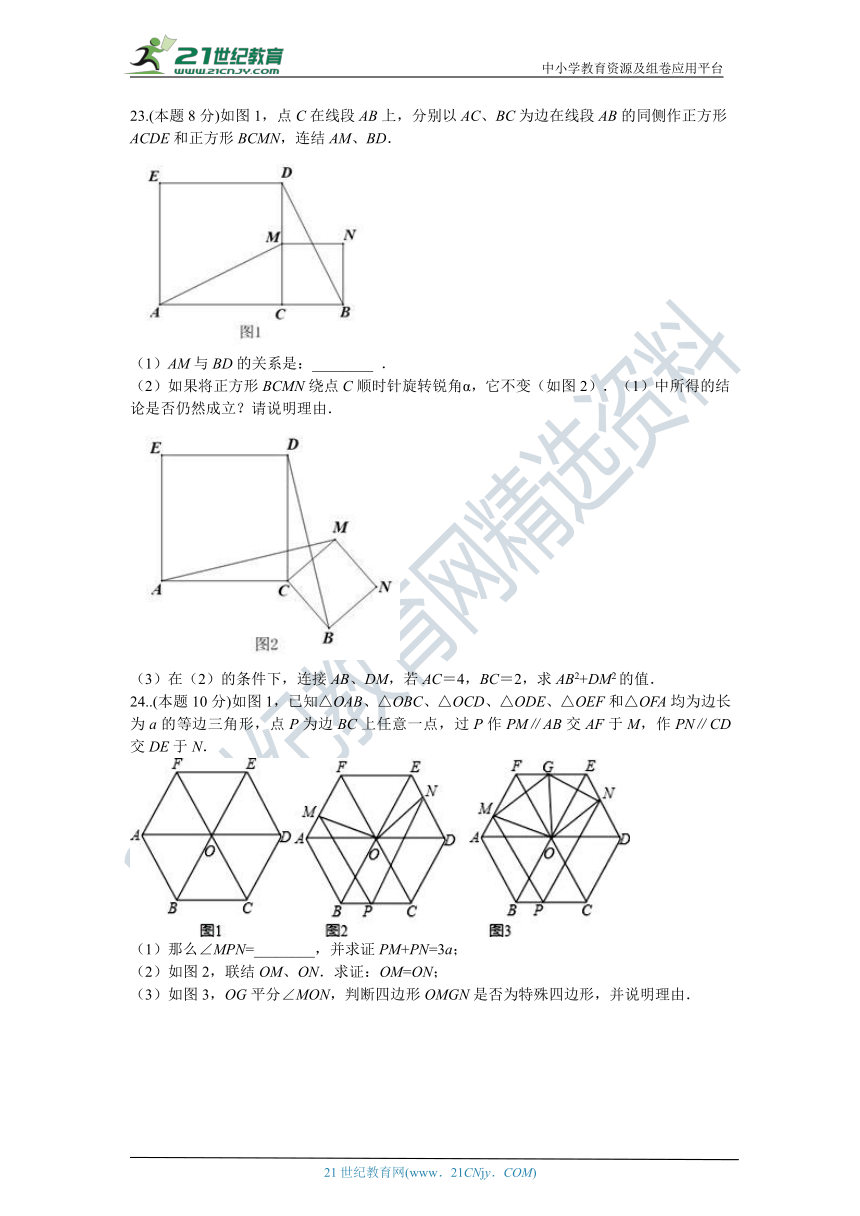
23.(本题8分)如图1,点C在线段AB上,分别以AC、BC为边在线段AB的同侧作正方形ACDE和正方形BCMN,连结AM、BD.
(1)AM与BD的关系是:________ .
(2)如果将正方形BCMN绕点C顺时针旋转锐角α,它不变(如图2).(1)中所得的结论是否仍然成立?请说明理由.
(3)在(2)的条件下,连接AB、DM,若AC=4,BC=2,求AB2+DM2的值.
24..(本题10分)如图1,已知△OAB、△OBC、△OCD、△ODE、△OEF和△OFA均为边长为a的等边三角形,点P为边BC上任意一点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)那么∠MPN=________,并求证PM+PN=3a;
(2)如图2,联结OM、ON.求证:OM=ON;
(3)如图3,OG平分∠MON,判断四边形OMGN是否为特殊四边形,并说明理由.
答案或解析
一、单选题
1. C 2. A 3. D 4. D 5. C
6.B 7. D 8.D 9.A 10. D
二、填空题
11. 24 12.22.5 13. 20
14. 15. 16.
17. .
【解答】∵四边形ABCD是正方形,
∴AD=CD=BC=AB,∠EAD=∠HDC=∠GCB=∠FBA=90°,
∵AE=BF=CG=DH,
∴△EAD≌△FBA≌△GCB≌△HDC(SAS),
∴∠EAP=∠HDE=∠FBQ=∠HCD,
∴∠QPS=∠ADE+∠DAP=∠BAF+∠DAP=∠BAD=90°,
同理∠PSR=90°,∠SRQ=90°,
∴四边形PSRQ是矩形,
∵∠HSD=∠GRC=∠APE=∠BQF=90°,∠GCR=∠HDS=∠EAP=∠QBF,CG=HD=AE=BF,
∴△CGR≌△BFQ≌△AEP≌△DHS,
∴CR=DS=AP=BQ,GR=HS=EP=QF,
∵△EAD≌△FBA≌△GCB≌△HDC,
∴DE=AF=BG=CH,
∴SR=SP,
∴矩形SPQR是正方形,
又∵S△ADE= ,
设△DHS的面积是a,设四边形HSPA的面积是b,
CH∥AF,S四边形PQRS=1×1﹣4(a+b)= ,
.
18.①②③④
【解答】①如图1,作AU⊥NQ于U,交BD于H,连接AN,AC,
∵∠AMN=∠ABC=90°,
∴A,B,N,M四点共圆,
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,
∴∠ANM=∠NAM=45°,
∴AM=MN;
②由同角的余角相等知,∠HAM=∠PMN,
∴Rt△AHM≌Rt△MPN,
∴MP=AH= AC= BD;
③∵∠BAN+∠QAD=∠NAQ=45°,
∴在∠NAM作AU=AB=AD,且使∠BAN=∠NAU,∠DAQ=∠QAU,
∴△ABN≌△UAN,△DAQ≌△UAQ,有∠UAN=∠UAQ,BN=NU,DQ=UQ,
∴点U在NQ上,有BN+DQ=QU+UN=NQ;
④如图2,作MS⊥AB,垂足为S,作MW⊥BC,垂足为W,点M是对角线BD上的点,
∴四边形SMWB是正方形,有MS=MW=BS=BW,
∴△AMS≌△NMW
∴AS=NW,
∴AB+BN=SB+BW=2BW,
∵BW:BM=1: ,
三、解答题
19.【答案】解:连接AC,BD交于点O,
∵四边形ABCD是菱形,
∴AO= AC=12厘米,AC⊥BD,
∴BO==5厘米,
∴BD=2BO=10厘米,
∴BM=3BD=30厘米.
20.【答案】解:如图,过点C作CH⊥AB交ABGFH,交DG于Q,
在直角三角形ABC中,由勾股定理得,AB=5.
由AB×CH=AC×BC得,CH=.第一种边长为,第二种情况下边长为
故第二种情况的正方形面积较大.
21.【答案】解答:解:延长PF交AB的延长线于点G , ,在△BGF与△CPF中, ,∴△BGF≌△CPF , ∴GF=PF , ∴F为PG中点.又∵EP⊥CD , ∴∠BEP=90°,∴EF= PG ,
∵PF= PG(中点定义),∴EF=PF , ∴∠FEP=∠EPF , ∵∠BEP=∠EPC=90°,∴∠BEP-∠FEP=∠EPC-∠EPF , 即∠BEF=∠FPC , ∵四边形ABCD为菱形,∴AB=BC , ∠ABC=180°-∠A=70°,∵E , F分别为AB , BC的中点,∴BE=BF , ∠BEF=∠BFE= (180°-70°)=55°,∴∠FPC=55°.
?
22.【答案】 (1)解:解方程x2-6x+8=0可得x=2或x=4,
∵BC、OC的长是方程x2-6x+8=0的两个根,且OC>BC,
∴BC=2,OC=4,
∴B(-2,4),
∵△ODE是△OCB绕点O顺时针旋转90°得到的,
∴OD=OC=4,DE=BC=2,
∴D(4,0),
设直线BD解析式为y=kx+b,∴直线BD的解析式为
(2)解:由(1)可知E(4,2), S△OFH=.
(3)解:∵以点D、F、M、N为顶点的四边形是矩形,
∴△DFM为直角三角形,
①当∠MFD=90°时,则M只能在x轴上,连接FN交MD于点G,如图1,
由(2)可知OF=,OD=4,
则有△MOF与△FOD形状要、相同,得OM= ,
∴,且D(4,0),∴,点N的坐标为
②当∠MDF=90°时,则M只能在y轴上,连接DN交MF于点G,如图2,
此时
③当∠FMD=90°时,则可知M点为O点,如图3,
可求得
综上可知存在满足条件的N点,其坐标为或或.
23.【答案】 (1)相等且垂直
(2)成立,
理由:∵四边形ACDE正方形,四边形BCMN正方形,
∴AC=CD? ? MC=BC? ?∠ACD=∠BCM=90°,
∴?∠ACD+∠DCM=∠BCM+∠DCM,
即∠ACM=∠BCD,
在△ACM与△DCB中,
∴AACM≌△DCB(SAS),
∴AM=BD ,∠MAC=∠BDC,
同(1)可证AM⊥DB,
∴AM=BD且AM⊥DB.
(3)解:如图,
∵AM⊥DB,
∴∠DOM=∠AOB=∠AOD=∠BOM=90°,
由勾股定理得OD2+OM2=DM2 , OD2+OA2=AD2 , OB2+OM2=MB2 , OA2+OB2=AB2 ,
∴AB2+DM2=OD2+OM2+OA2+OB2=AD2+BM2 ,
∵AD=AC=4 , BM=BC=2?,
∴AB2+DM2=(4)2+(2)2=40.
∵四边形ACDE正方形,四边形BCMN正方形,
∴AC=CD? ? MC=BC? ?∠ACD=∠BCM=90°,
∴△ACM≌DCB(SAS),
∴AM=BD ,∠MAC=∠BDC,
∵∠DMH=∠AMC,
∴∠DHM=∠ACM=90°,
∴AM⊥DB,
故答案为:相等且垂直.
24.【答案】(1)60°
(2)解:证明:由(1)得:六边形ABCDEF是正六边形,AB∥MP,PN∥DC,
∴AM=BP=EN,
∵∠MAO=∠OEN=60°,OA=OE,
在△OMA和△ONE中,
,A∴△OMA≌AONE(SAS)
∴OM=ON.
(3)解:四边形MONG是菱形;理由如下:
由(2)得,△OMA≌△ONE,
∴∠MOA=∠EON,
∵EF∥AO,AF∥OE,
∴四边形AOEF是平行四边形,
∴∠AFE=∠AOE=120°,
∴∠MON=120°,
∴∠GON=60°,
∵∠GOE=60°﹣∠EON,∠DON=60°﹣∠EON,
∴∠GOE=∠DON,
∵OD=OE,∠ODN=∠OEG,
在△GOE和△DON中,
∴△GOD≌△NOD(ADA),
∴OG=ON,
又∵∠GON=60°,
∴△ONG是等边三角形,
∴ON=NG,
又∵OM=ON,∠MOG=60°,
∴△MOG是等边三角形,
∴MG=GO=MO,
∴MO=ON=NG=MG,
∴四边形MONG是菱形.
【解析】【解答】(1)解:∵△OAB、△OBC、△OCD、△ODE、△OEF和△OFA均为边长为a的等边三角形
∴六边形ABCDEF是边长为a的正六边形,
∴∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°
又∴PM∥AB,PN∥CD,
∴∠BPM=60°,∠NPC=60°,
∴∠MPN=180°﹣∠BPM﹣∠NPC=180°﹣60°﹣60°=60°,
故答案为:60°;
作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,如图所示:
MP+PN=MG+GH+HP+PL+LK+KN
∵正六边形ABCDEF中,PM∥AB,作PN∥CD,
∵∠AMG=∠BPH=∠CPL=∠DNK=60°,
∴GM= AM,HP= BP,PL= PC,NK= ND,
∵AM=BP,PC=DN,
∴MG+HP+PL+KN=a,GH=LK=a,
∴MP+PN=MG+GH+HP+PL+LK+KN=3a.
第2题图 第3题图 第4题图 第5题图
第6题图 第7题图 第8题图 第9题图
第10题图
第12题图 第13题图 第14题图 第15题图
第16题图 第17题图 第18题图
21世纪教育网 www.21CNjy.COM 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21CNjy.COM)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
