浙教版数学八年级下册:第5章 特殊平行四边形 复习课件(共29张PPT)
文档属性
| 名称 | 浙教版数学八年级下册:第5章 特殊平行四边形 复习课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 471.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 07:57:57 | ||
图片预览





文档简介
(共29张PPT)
第5章 特殊平行四边形
复习课件
一、学习目标
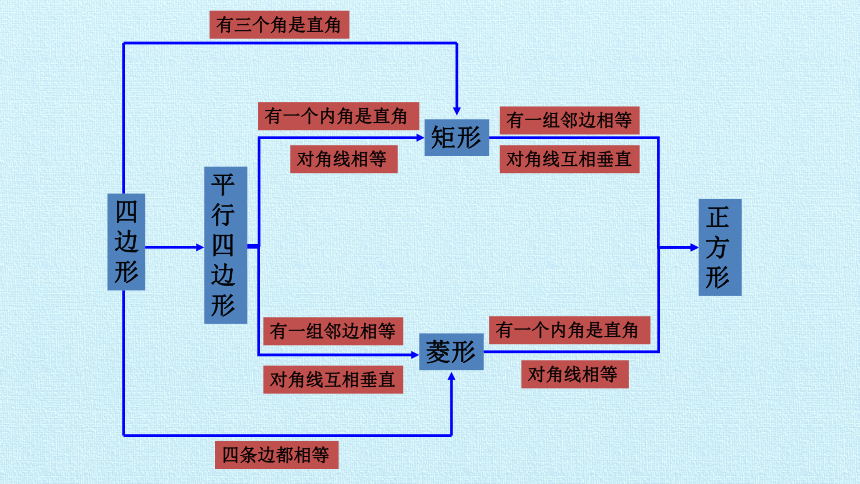
矩形、菱形、正方形
①了解平行四边形、矩形、菱形、正方形的关系a
②掌握矩形、菱形、正方形的概念b
③探索并掌握矩形、菱形、正方形的有关性质c
④探索并掌握四边形是矩形、菱形、正方形的条件c
⑤知道任意一个三角形、四边形或正方形可以镶嵌平面,并运用这几种图形进行简单的镶嵌设计b
平行四边形
四边形
矩形
菱形
正方形
有一个内角是直角
对角线相等
有一组邻边相等
对角线互相垂直
四条边都相等
有三个角是直角
有一组邻边相等
对角线互相垂直
有一个内角是直角
对角线相等
二、知识概要
性质 判定
边 两组对边分别平行
两组对边分别相等 有一个角是直角的平行四边形是矩形
角 矩形的四个角都是直角 有三个角是直角的四边形是矩形
对角线 矩形的两条对角线相等 对角线相等的平行四边形是矩形
推论 直角三角形斜边上的中线等于斜边的一半 如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形
(矩形)
二、知识概要
性质 判定
边 菱形的四条边都相等。
①一组邻边相等的平行四边形是菱形。
②四条边都相等的四边形是菱形。
角 ①对角相等
②邻角互补
对角线 菱形的两条对角线互相垂直;
并且每条对角线平分一组对角。
对角线互相垂直的平行四边形是菱形。
(菱形)
二、知识概要
性质 判定
边 正方形的四条边都相等 有一组邻边相等的矩形是正方形。
角 正方形的四个角都是直角。 有一个角是直角的菱形是正方形。
对角线 正方形的两条对角线相等,并且互相垂直平分。每条对角线平分一组对角。 ①对角线相等的菱形是正方形。
②对角线互相垂直的矩形是正方形。
(正方形)
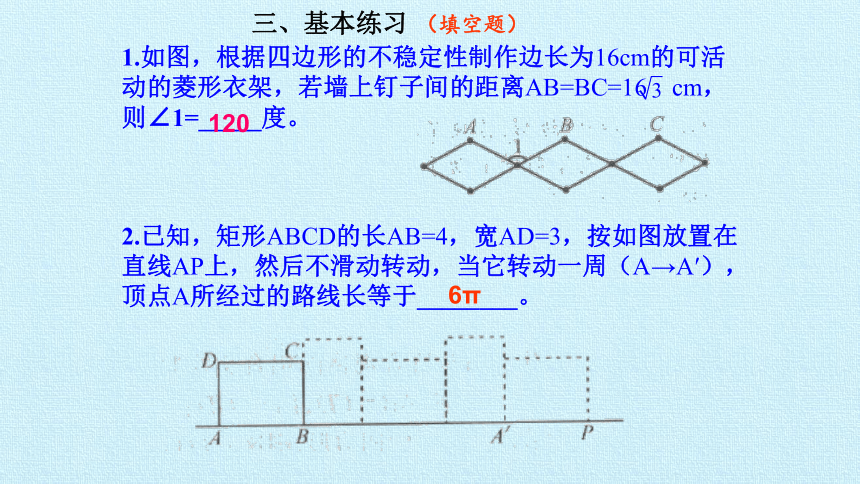
三、基本练习 (填空题)
1.如图,根据四边形的不稳定性制作边长为16cm的可活动的菱形衣架,若墙上钉子间的距离AB=BC=16 cm,则∠1=_____度。
2.已知,矩形ABCD的长AB=4,宽AD=3,按如图放置在直线AP上,然后不滑动转动,当它转动一周(A→A′),顶点A所经过的路线长等于________。
120
6π
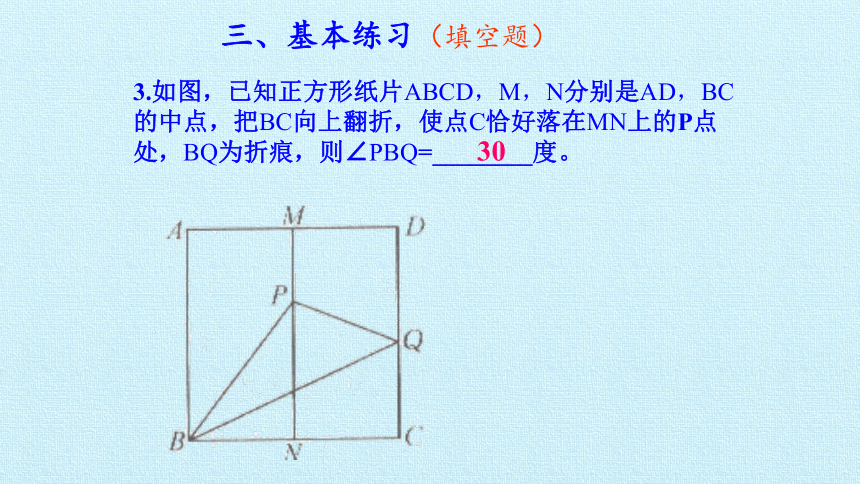
三、基本练习(填空题)
3.如图,已知正方形纸片ABCD,M,N分别是AD,BC的中点,把BC向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ=________度。
30
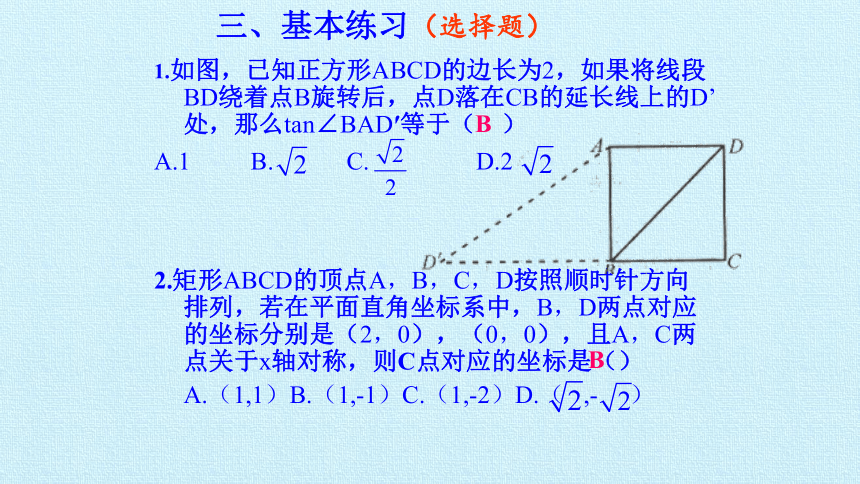
三、基本练习(选择题)
1.如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D’处,那么tan∠BAD′等于( )
A.1 B. C. D.2
2.矩形ABCD的顶点A,B,C,D按照顺时针方向排列,若在平面直角坐标系中,B,D两点对应的坐标分别是(2,0),(0,0),且A,C两点关于x轴对称,则C点对应的坐标是()
A.(1,1)B.(1,-1)C.(1,-2)D.( ,- )
B
B
(选择题)
3.如图,有一块矩形纸片ABCD,AB=10,AD=6,
将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为( )
A.4 B.6 C.8 D.10
C
三、基本练习
例1.工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,使AB=CD,EF=GH。
例1工人师傅做铝合金窗框分下面三个步骤进行:
(2)摆成如图所示的四边形,则这时窗框的形状______,根据的数学道理__________________。
平行四边形
两组对边分别相等的四边形是平行四边形
例1.工人师傅做铝合金窗框分下面三个步骤
进行:
(3)将直角尺靠紧窗框的一个角,调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,说明窗框合格,这时窗框是___形,根据的数学道理是____________________。
矩
有一个角是直角的平行四边形是矩形
还有什么方法可以说明这个铝合金窗框是合格的?
想一想
A
B
C
D
A
B
C
D
AC=BD
∠A=∠B=∠C=90°
A
B
C
D
o
60
若这个铝合金窗框ABCD两条对角线的夹角∠AOB为60°,△AOB的周长为3m。
(1)求窗框对角线AC长;
A
B
C
D
o
60
若这个铝合金窗框ABCD两条对角线的夹角∠AOB为60°,△AOB的周长为3m。
(2)求窗框ABCD的面积。
例2如图,两张等宽的纸条交叉重叠在一起,猜想重叠部分的四边形ABCD是什么形状?说说你的理由。
F
E
例3 将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你会发现这是一个菱形。你能解释其中的道理吗?
若展开后的菱形纸片ABCD中,两条对角线AC= ,BD=4。
(1)求菱形ABCD的面积;
(3)求∠ADC的度数。
(2)求菱形ABCD的周长;
如果想得到一个正方形,该怎么剪?并解释你这样做的道理。
想一想
例4 已知正方形ABCD
A
B
C
D
(1)若一条对角线BD长为2cm,求这个正方形的周长、面积。
例4 已知正方形ABCD
A
B
C
D
(2)若E为对角线上一点,连接EA、EC。EA=EC吗?说说你的理由。
E
例4 已知正方形ABCD
(3)若AB=BE,求∠AED的大小。
A
B
C
D
E
例5 顺次连接任意四边形各边的中点,所构成的四边形以下简称为“中点四边形”。试判断中点四边形EFGH的形状,并说明理由。
(1)添加一个条件,使四边形EFGH为菱形;
AC⊥BD
AC=BD
AC=BD且AC⊥BD
(2)添加一个条件,使四边形EFGH为矩形;
(3)添加一个条件,使四边形EFGH为正方形;
1.矩形的“中点四边形”是_____形;
2.菱形的“中点四边形”是_____形;
3.正方形的“中点四边形”是___形。
矩
菱
正方
那么,特殊平行四边形的“中点四边形”会是怎样的图形呢?
中考链接
1.如图,在矩形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。若AB=2,AD=4,则阴影部分的面积为( )
3
4
6
D. 8
B
中考链接
2. 如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是( )
3:4
5:8
9:16
D.1:2
B
3.已知正方形ABCD,ME⊥BD,MF⊥AC,垂足分别为E、F
(1)M是AD上的点,若对角线AC=12cm,求ME+MF的长。
A
B
C
D
O
M
F
E
(2)若M是AD上的一个动点,ME+MF的长度是否发生改变?
(3)当M点运动到何处时,四边形MFOE的面积最大?
谢 谢
第5章 特殊平行四边形
复习课件
一、学习目标
矩形、菱形、正方形
①了解平行四边形、矩形、菱形、正方形的关系a
②掌握矩形、菱形、正方形的概念b
③探索并掌握矩形、菱形、正方形的有关性质c
④探索并掌握四边形是矩形、菱形、正方形的条件c
⑤知道任意一个三角形、四边形或正方形可以镶嵌平面,并运用这几种图形进行简单的镶嵌设计b
平行四边形
四边形
矩形
菱形
正方形
有一个内角是直角
对角线相等
有一组邻边相等
对角线互相垂直
四条边都相等
有三个角是直角
有一组邻边相等
对角线互相垂直
有一个内角是直角
对角线相等
二、知识概要
性质 判定
边 两组对边分别平行
两组对边分别相等 有一个角是直角的平行四边形是矩形
角 矩形的四个角都是直角 有三个角是直角的四边形是矩形
对角线 矩形的两条对角线相等 对角线相等的平行四边形是矩形
推论 直角三角形斜边上的中线等于斜边的一半 如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形
(矩形)
二、知识概要
性质 判定
边 菱形的四条边都相等。
①一组邻边相等的平行四边形是菱形。
②四条边都相等的四边形是菱形。
角 ①对角相等
②邻角互补
对角线 菱形的两条对角线互相垂直;
并且每条对角线平分一组对角。
对角线互相垂直的平行四边形是菱形。
(菱形)
二、知识概要
性质 判定
边 正方形的四条边都相等 有一组邻边相等的矩形是正方形。
角 正方形的四个角都是直角。 有一个角是直角的菱形是正方形。
对角线 正方形的两条对角线相等,并且互相垂直平分。每条对角线平分一组对角。 ①对角线相等的菱形是正方形。
②对角线互相垂直的矩形是正方形。
(正方形)
三、基本练习 (填空题)
1.如图,根据四边形的不稳定性制作边长为16cm的可活动的菱形衣架,若墙上钉子间的距离AB=BC=16 cm,则∠1=_____度。
2.已知,矩形ABCD的长AB=4,宽AD=3,按如图放置在直线AP上,然后不滑动转动,当它转动一周(A→A′),顶点A所经过的路线长等于________。
120
6π
三、基本练习(填空题)
3.如图,已知正方形纸片ABCD,M,N分别是AD,BC的中点,把BC向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ=________度。
30
三、基本练习(选择题)
1.如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D’处,那么tan∠BAD′等于( )
A.1 B. C. D.2
2.矩形ABCD的顶点A,B,C,D按照顺时针方向排列,若在平面直角坐标系中,B,D两点对应的坐标分别是(2,0),(0,0),且A,C两点关于x轴对称,则C点对应的坐标是()
A.(1,1)B.(1,-1)C.(1,-2)D.( ,- )
B
B
(选择题)
3.如图,有一块矩形纸片ABCD,AB=10,AD=6,
将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为( )
A.4 B.6 C.8 D.10
C
三、基本练习
例1.工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,使AB=CD,EF=GH。
例1工人师傅做铝合金窗框分下面三个步骤进行:
(2)摆成如图所示的四边形,则这时窗框的形状______,根据的数学道理__________________。
平行四边形
两组对边分别相等的四边形是平行四边形
例1.工人师傅做铝合金窗框分下面三个步骤
进行:
(3)将直角尺靠紧窗框的一个角,调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,说明窗框合格,这时窗框是___形,根据的数学道理是____________________。
矩
有一个角是直角的平行四边形是矩形
还有什么方法可以说明这个铝合金窗框是合格的?
想一想
A
B
C
D
A
B
C
D
AC=BD
∠A=∠B=∠C=90°
A
B
C
D
o
60
若这个铝合金窗框ABCD两条对角线的夹角∠AOB为60°,△AOB的周长为3m。
(1)求窗框对角线AC长;
A
B
C
D
o
60
若这个铝合金窗框ABCD两条对角线的夹角∠AOB为60°,△AOB的周长为3m。
(2)求窗框ABCD的面积。
例2如图,两张等宽的纸条交叉重叠在一起,猜想重叠部分的四边形ABCD是什么形状?说说你的理由。
F
E
例3 将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你会发现这是一个菱形。你能解释其中的道理吗?
若展开后的菱形纸片ABCD中,两条对角线AC= ,BD=4。
(1)求菱形ABCD的面积;
(3)求∠ADC的度数。
(2)求菱形ABCD的周长;
如果想得到一个正方形,该怎么剪?并解释你这样做的道理。
想一想
例4 已知正方形ABCD
A
B
C
D
(1)若一条对角线BD长为2cm,求这个正方形的周长、面积。
例4 已知正方形ABCD
A
B
C
D
(2)若E为对角线上一点,连接EA、EC。EA=EC吗?说说你的理由。
E
例4 已知正方形ABCD
(3)若AB=BE,求∠AED的大小。
A
B
C
D
E
例5 顺次连接任意四边形各边的中点,所构成的四边形以下简称为“中点四边形”。试判断中点四边形EFGH的形状,并说明理由。
(1)添加一个条件,使四边形EFGH为菱形;
AC⊥BD
AC=BD
AC=BD且AC⊥BD
(2)添加一个条件,使四边形EFGH为矩形;
(3)添加一个条件,使四边形EFGH为正方形;
1.矩形的“中点四边形”是_____形;
2.菱形的“中点四边形”是_____形;
3.正方形的“中点四边形”是___形。
矩
菱
正方
那么,特殊平行四边形的“中点四边形”会是怎样的图形呢?
中考链接
1.如图,在矩形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。若AB=2,AD=4,则阴影部分的面积为( )
3
4
6
D. 8
B
中考链接
2. 如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是( )
3:4
5:8
9:16
D.1:2
B
3.已知正方形ABCD,ME⊥BD,MF⊥AC,垂足分别为E、F
(1)M是AD上的点,若对角线AC=12cm,求ME+MF的长。
A
B
C
D
O
M
F
E
(2)若M是AD上的一个动点,ME+MF的长度是否发生改变?
(3)当M点运动到何处时,四边形MFOE的面积最大?
谢 谢
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
