5.2.2 菱形的判定同步测试题(含解析)
文档属性
| 名称 | 5.2.2 菱形的判定同步测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-14 15:59:59 | ||
图片预览




文档简介
5.2.2 菱形的判定测试卷
(时间45分钟 满分100分)
一.选择题(每小题7分,共42分)
1.(2019?浦东新区二模)已知在四边形ABCD中,AD∥BC,对角线AC与BD相交于点O,AO=CO,如果添加下列一个条件后,就能判定这个四边形是菱形的是( )
A.BO=DO B.AB=BC C.AB=CD D.AB∥CD
2.(2019?铅山县一模)已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为菱形的是( )
A.AC⊥BD B.∠ABD=∠ADB C.AB=CD D.AB=BC
3.(2019秋?历下区期中)下列条件中,能判断四边形是菱形的是( )
A.对角线互相平分且垂直的四边形
B.对角线互相垂直的四边形
C.对角线互相垂直且相等的四边形
D.对角线相等的平行四边形
4.(2018秋?太原期中)如图,△ABC中,点P是AB边上的一点,过点P作PD∥BC,PE∥AC,分别交AC,BC于点D,E,连按CP.若四边形CDPE是菱形,则线段CP应满足的条件是( )
A.CP平分∠ACB B.CP⊥AB
C.CP是AB边上的中线 D.CP=AP
5.(2018春?西城区校级期中)在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90° B.AC⊥BD C.AB=CD D.∠A=∠C
6.(2018春?南昌期中)四边形的四边长顺次为a、b、c、d,且a2+b2+c2+d2=ab+bc+cd+ad,则此四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
二.填空题(每小题7分,共28分)
7.(2019春?思明区校级期中)平面直角坐标系中,四边形ABCD的顶点坐标分别是A(﹣1,m)、B(﹣4,0)、C(1,0)、D(a,m),且m>0,若以点A、B、C、D为顶点的四边形是菱形,则点D的坐标为 .
8.(2019春?北流市期中)如图在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= 时,平行四边形CDEB为菱形.
9.(2019秋?榕城区期中)如图,小华剪了两条宽为3的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为 .
10.(2019春?仓山区期中)如图,已知∠A,以点A为圆心,恰当长为半径画弧,分别交AE,AF于点B,D,继续分别以点B,D为圆心,线段AB长为半径画弧交于点C,连接BC,CD,则所四得边形ABCD为菱形,判定依据是: .
三.解答题(共30分)
11.(10分)(2019秋?景泰县校级期中)已知:如图,在?ABCD中,对角线AC与BD相交于点O,AB=,OA=2,OB=1,求证:?ABCD是菱形.
12.(10分)(2019春?广安区校级期中)如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交
AD于点F,AE与BF交于点O,连接EF.
求证:四边形ABEF是菱形.
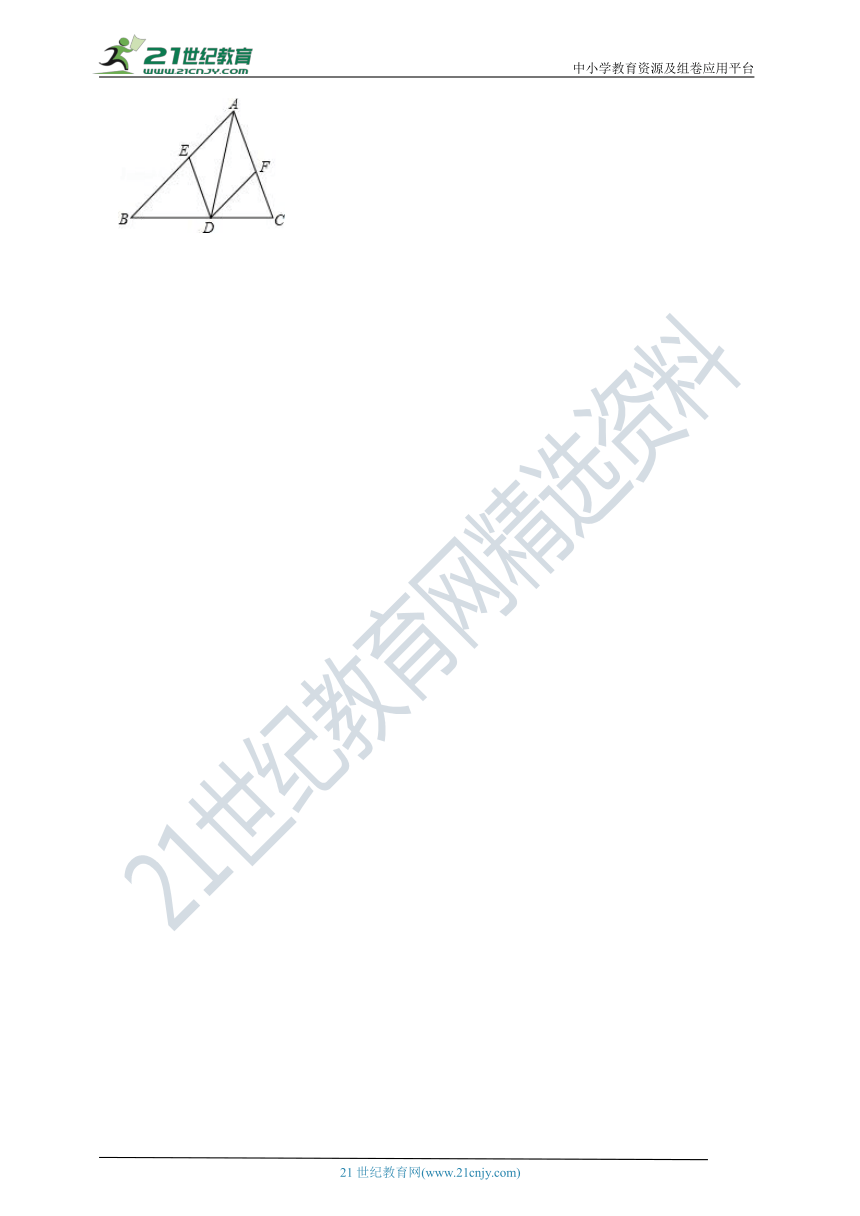
13.(10分)(2019春?丹江口市期中)如图,△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)试判断四边形AEDF的形状.
(2)当△ABC满足 条件时,EF∥BC;当△ABC满足 条件时,EF=AD.
5.2.2 菱形的判定测试卷
参考答案与试题解析
一.选择题
1.(2019?浦东新区二模)已知在四边形ABCD中,AD∥BC,对角线AC与BD相交于点O,AO=CO,如果添加下列一个条件后,就能判定这个四边形是菱形的是( )
A.BO=DO B.AB=BC C.AB=CD D.AB∥CD
【分析】根据平行线的性质得到∠ADB=∠CBD,根据全等三角形的性质得到AD=BC,于是得到四边形ABCD是平行四边形,根据菱形的判定定理即可得到即可.
【解答】解:∵AD∥BC,
∴∠ADB=∠CBD,
在△ADO与△CBO中,,
∴△ADO≌△CBO(AAS),
∴AD=CB,
∴四边形ABCD是平行四边形,
∵AB=BC
∴四边形ABCD是菱形;故B正确;
故选:B.
2.(2019?铅山县一模)已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为菱形的是( )
A.AC⊥BD B.∠ABD=∠ADB C.AB=CD D.AB=BC
【分析】①定义:一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形.据此判断即可.
【解答】解:A、由对角线互相垂直平分的平行四边形是菱形,故A选项正确;
B、由一条对角线平分一角,可得出一组邻边相等,也能判定为菱形,故B选项正确;
C、由平行四边形的性质可得AB=CD,即不能判定平行四边形ABCD是菱形,故C选项不正确
D、由一组邻边相等平行四边形是菱形,故D选项正确.
故选:C.
3.(2019秋?历下区期中)下列条件中,能判断四边形是菱形的是( )
A.对角线互相平分且垂直的四边形
B.对角线互相垂直的四边形
C.对角线互相垂直且相等的四边形
D.对角线相等的平行四边形
【分析】利用菱形的判定方法对各个选项一一进行判断即可.
【解答】解:A、对角线互相平分且垂直的四边形是菱形,符合题意;
B、对角线互相平分且垂直的四边形是菱形,对角线互相垂直的四边形不一定是菱形,不符合题意;
C、对角线互相平分且垂直的四边形是菱形,对角线互相垂直且相等的四边形不一定是菱形.不符合题意;
D、对角线互相平分且垂直的四边形是菱形,对角线相等的平行四边形不是菱形,不符合题意;
故选:A.
4.(2018秋?太原期中)如图,△ABC中,点P是AB边上的一点,过点P作PD∥BC,PE∥AC,分别交AC,BC于点D,E,连按CP.若四边形CDPE是菱形,则线段CP应满足的条件是( )
A.CP平分∠ACB B.CP⊥AB
C.CP是AB边上的中线 D.CP=AP
【分析】根据菱形的性质解答即可.
【解答】解:∵四边形CDPE是菱形,
∴∠DCP=∠ECP,
∴CP平分∠ACB,
故选:A.
5.(2018春?西城区校级期中)在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90° B.AC⊥BD C.AB=CD D.∠A=∠C
【分析】由在四边形ABCD中,对角线AC,BD互相平分,可得四边形ABCD是平行四边形,又由对角线互相垂直的平行四边形是菱形,即可求得答案.
【解答】解:∵在四边形ABCD中,对角线AC,BD互相平分,
∴四边形ABCD是平行四边形,
∴当AC⊥BD时,四边形ABCD是菱形.
故选:B.
6.(2018春?南昌期中)四边形的四边长顺次为a、b、c、d,且a2+b2+c2+d2=ab+bc+cd+ad,则此四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
【分析】本题可通过整理配方式子a2+b2+c2+d2=ab+bc+cd+ad得到(a﹣b)2+(b﹣c)2+(c﹣d)2+(a﹣d)2=0,从而得出a=b=c=d,∴四边形一定是菱形.
【解答】解:整理配方式子a2+b2+c2+d2=ab+bc+cd+ad,
2(a2+b2+c2+d2)=2(ab+bc+cd+ad),
∴(a﹣b)2+(b﹣c)2+(c﹣d)2+(a﹣d)2=0,
由非负数的性质可知:(a﹣b)=0,(b﹣c)=0,(c﹣d)=0,(a﹣d)=0,
∴a=b=c=d,
∴四边形一定是菱形,
故选:C.
二.填空题
7.(2019春?思明区校级期中)平面直角坐标系中,四边形ABCD的顶点坐标分别是A(﹣1,m)、B(﹣4,0)、C(1,0)、D(a,m),且m>0,若以点A、B、C、D为顶点的四边形是菱形,则点D的坐标为 (4,4)或(﹣5,) .
【分析】作AM⊥BC于M,由题意得出AD∥BC,OB=4,OC=1,OM=1得出AD=BC=5,BM=3,CM=2,①当点D在y轴的右侧时,由菱形的性质得出AB=BC=5,由勾股定理得出AM==4,得出点D的坐标为(4,4);
②当点D在y轴的左侧时,由菱形的性质得出AB=BC=5,由勾股定理得出AM==,得出点D的坐标为(﹣6,).
【解答】解:作AM⊥BC于M,
∵A(﹣1,m)、B(﹣4,0)、C(1,0)、D(a,m),且m>0,
∴AD∥BC,OB=4,OC=1,OM=1,
∴AD=BC=5,BM=3,CM=2,
分两种情况:
①当点D在y轴的右侧时,如图1所示:
∵以点A、B、C、D为顶点的四边形是菱形,
∴AB=BC=5,
∴AM===4,
∴点D的坐标为(4,4);
②当点D在y轴的左侧时,如图2所示:
∵以点A、B、C、D为顶点的四边形是菱形,
∴AB=BC=5,
∴AM===,
∴点D的坐标为(﹣6,);
综上所述,若以点A、B、C、D为顶点的四边形是菱形,则点D的坐标为(4,4)或(﹣6,);
故答案为:(4,4)或(﹣6,).
8.(2019春?北流市期中)如图在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= 时,平行四边形CDEB为菱形.
【分析】首先根据勾股定理求得AB=10,由菱形的性质可得OD=OB,CD=CB,根据勾股定理可得OB的值,由AD=AB﹣2OB可求AD的长.
【解答】解:如图,连接CE交AB于点O.
∵Rt△ABC中,∠ACB=90°,AC=8,BC=6,
∴AB==10
若平行四边形CDEB为菱形时,CE⊥BD,OD=OB,CD=CB.
∵AB?OC=AC?BC,
∴OC=.
∴OB==
∴AD=AB﹣2OB=
故答案为:
9.(2019秋?榕城区期中)如图,小华剪了两条宽为3的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为 6 .
【分析】首先过点B作BE⊥AD于点E,BF⊥CD于点F,由题意可得四边形ABCD是平行四边形,继而求得AB=BC的长,判定四边形ABCD是菱形,则可求得答案.
【解答】解:过点B作BE⊥AD于点E,BF⊥CD于点F,
根据题意得:AD∥BC,AB∥CD,BE=BF=3,
∴四边形ABCD是平行四边形,
∵∠BAD=∠BCD=60°,
∴∠ABE=∠CBF=30°,
∴AB=2AE,BC=2CF,
∵AB2=AE2+BE2,
∴AB=,
同理:BC=2,
∴AB=BC,
∴四边形ABCD是菱形,
∴AD=2,
∴S菱形ABCD=AD?BE=6.
故答案为:6.
10.(2019春?仓山区期中)如图,已知∠A,以点A为圆心,恰当长为半径画弧,分别交AE,AF于点B,D,继续分别以点B,D为圆心,线段AB长为半径画弧交于点C,连接BC,CD,则所四得边形ABCD为菱形,判定依据是: 四条边相等的四边形是菱形 .
【分析】根据四条边相等的四边形是菱形即可求解.
【解答】解:∵已知∠A,以点A为圆心,恰当长为半径画弧,分别交AE,AF于点B,D,
∴AB=AD,
∵分别以点B,D为圆心,线段AB长为半径画弧交于点C,
∴BC=CD=AB,
∴AB=AD=BC=CD,
∴所得四边形ABCD为菱形,判定依据是:四条边相等的四边形是菱形.
故答案为:四条边相等的四边形是菱形.
三.解答题
11.(2019秋?景泰县校级期中)已知:如图,在?ABCD中,对角线AC与BD相交于点O,AB=,OA=2,OB=1,求证:?ABCD是菱形.
【分析】根据利用勾股定理的逆定理可证明∠AOB=90°,得出AC⊥BD,根据对角线互相垂直的平行四边形是菱形可得解.
【解答】证明:在△AOB中,AB=,OA=2,OB=1,
∴AO2+OB2=22+1=5,
又∵AB2=()2=5,
∴AO2+OB2=AB2,
∴∠AOB=90°,
∴AC⊥BD;
∵四边形ABCD是平行四边形,
∴?ABCD是菱形.
12.(2019春?广安区校级期中)如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交
AD于点F,AE与BF交于点O,连接EF.
求证:四边形ABEF是菱形.
【分析】由四边形ABCD是平行四边形,得到AD∥BC,从而得到∠AFB=∠FBE,再由∠ABF=∠FBE,推出∠ABF=∠AFB,于是得到AB=AF,同理得出AB=BE,证出四边形ABEF是平行四边形,即可得出结论.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFB=∠FBE,
∵BF平分∠ABC,
∴∠ABF=∠FBE,
∴∠ABF=∠AFB,
∴AB=AF,
同理AB=BE,
∴AF=BE,
∵AB=BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形.
13.(2019春?丹江口市期中)如图,△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)试判断四边形AEDF的形状.
(2)当△ABC满足 AB=AC 条件时,EF∥BC;当△ABC满足 ∠BAC=90° 条件时,EF=AD.
【分析】(1)根据DE∥AC交AB于点E,DF∥AB交AC于点F,可以判断四边形AEDF是平行四边形,再根据角平分线的性质和平行线的性质即可证明结论成立;
(2)由菱形的性质、等腰三角形的性质以及正方形的性质即可得出答案.
【解答】解:(1)四边形AEDF是菱形;理由如下:
∵DE∥AC交AB于点E,DF∥AB交AC于点F,
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∴∠ADF=∠FAD,
∴FA=FD,
∴四边形AEDF是菱形;
(2)当△ABC满足AB=AC条件时,EF∥BC;当△ABC满足∠BAC=90°条件时,EF=AD.理由如下:
由(1)得:四边形AEDF是菱形,
∴AD⊥EF,
∵AB=AC,AD是角平分线,
∴AD⊥BC,
∴EF∥BC;
当∠ABC=90°时,四边形AEDF是正方形,
∴EF=AD;
故答案为:AB=AC,∠BAC=90°.
(时间45分钟 满分100分)
一.选择题(每小题7分,共42分)
1.(2019?浦东新区二模)已知在四边形ABCD中,AD∥BC,对角线AC与BD相交于点O,AO=CO,如果添加下列一个条件后,就能判定这个四边形是菱形的是( )
A.BO=DO B.AB=BC C.AB=CD D.AB∥CD
2.(2019?铅山县一模)已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为菱形的是( )
A.AC⊥BD B.∠ABD=∠ADB C.AB=CD D.AB=BC
3.(2019秋?历下区期中)下列条件中,能判断四边形是菱形的是( )
A.对角线互相平分且垂直的四边形
B.对角线互相垂直的四边形
C.对角线互相垂直且相等的四边形
D.对角线相等的平行四边形
4.(2018秋?太原期中)如图,△ABC中,点P是AB边上的一点,过点P作PD∥BC,PE∥AC,分别交AC,BC于点D,E,连按CP.若四边形CDPE是菱形,则线段CP应满足的条件是( )
A.CP平分∠ACB B.CP⊥AB
C.CP是AB边上的中线 D.CP=AP
5.(2018春?西城区校级期中)在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90° B.AC⊥BD C.AB=CD D.∠A=∠C
6.(2018春?南昌期中)四边形的四边长顺次为a、b、c、d,且a2+b2+c2+d2=ab+bc+cd+ad,则此四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
二.填空题(每小题7分,共28分)
7.(2019春?思明区校级期中)平面直角坐标系中,四边形ABCD的顶点坐标分别是A(﹣1,m)、B(﹣4,0)、C(1,0)、D(a,m),且m>0,若以点A、B、C、D为顶点的四边形是菱形,则点D的坐标为 .
8.(2019春?北流市期中)如图在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= 时,平行四边形CDEB为菱形.
9.(2019秋?榕城区期中)如图,小华剪了两条宽为3的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为 .
10.(2019春?仓山区期中)如图,已知∠A,以点A为圆心,恰当长为半径画弧,分别交AE,AF于点B,D,继续分别以点B,D为圆心,线段AB长为半径画弧交于点C,连接BC,CD,则所四得边形ABCD为菱形,判定依据是: .
三.解答题(共30分)
11.(10分)(2019秋?景泰县校级期中)已知:如图,在?ABCD中,对角线AC与BD相交于点O,AB=,OA=2,OB=1,求证:?ABCD是菱形.
12.(10分)(2019春?广安区校级期中)如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交
AD于点F,AE与BF交于点O,连接EF.
求证:四边形ABEF是菱形.
13.(10分)(2019春?丹江口市期中)如图,△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)试判断四边形AEDF的形状.
(2)当△ABC满足 条件时,EF∥BC;当△ABC满足 条件时,EF=AD.
5.2.2 菱形的判定测试卷
参考答案与试题解析
一.选择题
1.(2019?浦东新区二模)已知在四边形ABCD中,AD∥BC,对角线AC与BD相交于点O,AO=CO,如果添加下列一个条件后,就能判定这个四边形是菱形的是( )
A.BO=DO B.AB=BC C.AB=CD D.AB∥CD
【分析】根据平行线的性质得到∠ADB=∠CBD,根据全等三角形的性质得到AD=BC,于是得到四边形ABCD是平行四边形,根据菱形的判定定理即可得到即可.
【解答】解:∵AD∥BC,
∴∠ADB=∠CBD,
在△ADO与△CBO中,,
∴△ADO≌△CBO(AAS),
∴AD=CB,
∴四边形ABCD是平行四边形,
∵AB=BC
∴四边形ABCD是菱形;故B正确;
故选:B.
2.(2019?铅山县一模)已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为菱形的是( )
A.AC⊥BD B.∠ABD=∠ADB C.AB=CD D.AB=BC
【分析】①定义:一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形.据此判断即可.
【解答】解:A、由对角线互相垂直平分的平行四边形是菱形,故A选项正确;
B、由一条对角线平分一角,可得出一组邻边相等,也能判定为菱形,故B选项正确;
C、由平行四边形的性质可得AB=CD,即不能判定平行四边形ABCD是菱形,故C选项不正确
D、由一组邻边相等平行四边形是菱形,故D选项正确.
故选:C.
3.(2019秋?历下区期中)下列条件中,能判断四边形是菱形的是( )
A.对角线互相平分且垂直的四边形
B.对角线互相垂直的四边形
C.对角线互相垂直且相等的四边形
D.对角线相等的平行四边形
【分析】利用菱形的判定方法对各个选项一一进行判断即可.
【解答】解:A、对角线互相平分且垂直的四边形是菱形,符合题意;
B、对角线互相平分且垂直的四边形是菱形,对角线互相垂直的四边形不一定是菱形,不符合题意;
C、对角线互相平分且垂直的四边形是菱形,对角线互相垂直且相等的四边形不一定是菱形.不符合题意;
D、对角线互相平分且垂直的四边形是菱形,对角线相等的平行四边形不是菱形,不符合题意;
故选:A.
4.(2018秋?太原期中)如图,△ABC中,点P是AB边上的一点,过点P作PD∥BC,PE∥AC,分别交AC,BC于点D,E,连按CP.若四边形CDPE是菱形,则线段CP应满足的条件是( )
A.CP平分∠ACB B.CP⊥AB
C.CP是AB边上的中线 D.CP=AP
【分析】根据菱形的性质解答即可.
【解答】解:∵四边形CDPE是菱形,
∴∠DCP=∠ECP,
∴CP平分∠ACB,
故选:A.
5.(2018春?西城区校级期中)在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90° B.AC⊥BD C.AB=CD D.∠A=∠C
【分析】由在四边形ABCD中,对角线AC,BD互相平分,可得四边形ABCD是平行四边形,又由对角线互相垂直的平行四边形是菱形,即可求得答案.
【解答】解:∵在四边形ABCD中,对角线AC,BD互相平分,
∴四边形ABCD是平行四边形,
∴当AC⊥BD时,四边形ABCD是菱形.
故选:B.
6.(2018春?南昌期中)四边形的四边长顺次为a、b、c、d,且a2+b2+c2+d2=ab+bc+cd+ad,则此四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
【分析】本题可通过整理配方式子a2+b2+c2+d2=ab+bc+cd+ad得到(a﹣b)2+(b﹣c)2+(c﹣d)2+(a﹣d)2=0,从而得出a=b=c=d,∴四边形一定是菱形.
【解答】解:整理配方式子a2+b2+c2+d2=ab+bc+cd+ad,
2(a2+b2+c2+d2)=2(ab+bc+cd+ad),
∴(a﹣b)2+(b﹣c)2+(c﹣d)2+(a﹣d)2=0,
由非负数的性质可知:(a﹣b)=0,(b﹣c)=0,(c﹣d)=0,(a﹣d)=0,
∴a=b=c=d,
∴四边形一定是菱形,
故选:C.
二.填空题
7.(2019春?思明区校级期中)平面直角坐标系中,四边形ABCD的顶点坐标分别是A(﹣1,m)、B(﹣4,0)、C(1,0)、D(a,m),且m>0,若以点A、B、C、D为顶点的四边形是菱形,则点D的坐标为 (4,4)或(﹣5,) .
【分析】作AM⊥BC于M,由题意得出AD∥BC,OB=4,OC=1,OM=1得出AD=BC=5,BM=3,CM=2,①当点D在y轴的右侧时,由菱形的性质得出AB=BC=5,由勾股定理得出AM==4,得出点D的坐标为(4,4);
②当点D在y轴的左侧时,由菱形的性质得出AB=BC=5,由勾股定理得出AM==,得出点D的坐标为(﹣6,).
【解答】解:作AM⊥BC于M,
∵A(﹣1,m)、B(﹣4,0)、C(1,0)、D(a,m),且m>0,
∴AD∥BC,OB=4,OC=1,OM=1,
∴AD=BC=5,BM=3,CM=2,
分两种情况:
①当点D在y轴的右侧时,如图1所示:
∵以点A、B、C、D为顶点的四边形是菱形,
∴AB=BC=5,
∴AM===4,
∴点D的坐标为(4,4);
②当点D在y轴的左侧时,如图2所示:
∵以点A、B、C、D为顶点的四边形是菱形,
∴AB=BC=5,
∴AM===,
∴点D的坐标为(﹣6,);
综上所述,若以点A、B、C、D为顶点的四边形是菱形,则点D的坐标为(4,4)或(﹣6,);
故答案为:(4,4)或(﹣6,).
8.(2019春?北流市期中)如图在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= 时,平行四边形CDEB为菱形.
【分析】首先根据勾股定理求得AB=10,由菱形的性质可得OD=OB,CD=CB,根据勾股定理可得OB的值,由AD=AB﹣2OB可求AD的长.
【解答】解:如图,连接CE交AB于点O.
∵Rt△ABC中,∠ACB=90°,AC=8,BC=6,
∴AB==10
若平行四边形CDEB为菱形时,CE⊥BD,OD=OB,CD=CB.
∵AB?OC=AC?BC,
∴OC=.
∴OB==
∴AD=AB﹣2OB=
故答案为:
9.(2019秋?榕城区期中)如图,小华剪了两条宽为3的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为 6 .
【分析】首先过点B作BE⊥AD于点E,BF⊥CD于点F,由题意可得四边形ABCD是平行四边形,继而求得AB=BC的长,判定四边形ABCD是菱形,则可求得答案.
【解答】解:过点B作BE⊥AD于点E,BF⊥CD于点F,
根据题意得:AD∥BC,AB∥CD,BE=BF=3,
∴四边形ABCD是平行四边形,
∵∠BAD=∠BCD=60°,
∴∠ABE=∠CBF=30°,
∴AB=2AE,BC=2CF,
∵AB2=AE2+BE2,
∴AB=,
同理:BC=2,
∴AB=BC,
∴四边形ABCD是菱形,
∴AD=2,
∴S菱形ABCD=AD?BE=6.
故答案为:6.
10.(2019春?仓山区期中)如图,已知∠A,以点A为圆心,恰当长为半径画弧,分别交AE,AF于点B,D,继续分别以点B,D为圆心,线段AB长为半径画弧交于点C,连接BC,CD,则所四得边形ABCD为菱形,判定依据是: 四条边相等的四边形是菱形 .
【分析】根据四条边相等的四边形是菱形即可求解.
【解答】解:∵已知∠A,以点A为圆心,恰当长为半径画弧,分别交AE,AF于点B,D,
∴AB=AD,
∵分别以点B,D为圆心,线段AB长为半径画弧交于点C,
∴BC=CD=AB,
∴AB=AD=BC=CD,
∴所得四边形ABCD为菱形,判定依据是:四条边相等的四边形是菱形.
故答案为:四条边相等的四边形是菱形.
三.解答题
11.(2019秋?景泰县校级期中)已知:如图,在?ABCD中,对角线AC与BD相交于点O,AB=,OA=2,OB=1,求证:?ABCD是菱形.
【分析】根据利用勾股定理的逆定理可证明∠AOB=90°,得出AC⊥BD,根据对角线互相垂直的平行四边形是菱形可得解.
【解答】证明:在△AOB中,AB=,OA=2,OB=1,
∴AO2+OB2=22+1=5,
又∵AB2=()2=5,
∴AO2+OB2=AB2,
∴∠AOB=90°,
∴AC⊥BD;
∵四边形ABCD是平行四边形,
∴?ABCD是菱形.
12.(2019春?广安区校级期中)如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交
AD于点F,AE与BF交于点O,连接EF.
求证:四边形ABEF是菱形.
【分析】由四边形ABCD是平行四边形,得到AD∥BC,从而得到∠AFB=∠FBE,再由∠ABF=∠FBE,推出∠ABF=∠AFB,于是得到AB=AF,同理得出AB=BE,证出四边形ABEF是平行四边形,即可得出结论.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFB=∠FBE,
∵BF平分∠ABC,
∴∠ABF=∠FBE,
∴∠ABF=∠AFB,
∴AB=AF,
同理AB=BE,
∴AF=BE,
∵AB=BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形.
13.(2019春?丹江口市期中)如图,△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)试判断四边形AEDF的形状.
(2)当△ABC满足 AB=AC 条件时,EF∥BC;当△ABC满足 ∠BAC=90° 条件时,EF=AD.
【分析】(1)根据DE∥AC交AB于点E,DF∥AB交AC于点F,可以判断四边形AEDF是平行四边形,再根据角平分线的性质和平行线的性质即可证明结论成立;
(2)由菱形的性质、等腰三角形的性质以及正方形的性质即可得出答案.
【解答】解:(1)四边形AEDF是菱形;理由如下:
∵DE∥AC交AB于点E,DF∥AB交AC于点F,
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∴∠ADF=∠FAD,
∴FA=FD,
∴四边形AEDF是菱形;
(2)当△ABC满足AB=AC条件时,EF∥BC;当△ABC满足∠BAC=90°条件时,EF=AD.理由如下:
由(1)得:四边形AEDF是菱形,
∴AD⊥EF,
∵AB=AC,AD是角平分线,
∴AD⊥BC,
∴EF∥BC;
当∠ABC=90°时,四边形AEDF是正方形,
∴EF=AD;
故答案为:AB=AC,∠BAC=90°.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
