初中数学浙教版九年级下册3.3 由三视图描述几何体 基础巩固训练(含解析)
文档属性
| 名称 | 初中数学浙教版九年级下册3.3 由三视图描述几何体 基础巩固训练(含解析) | 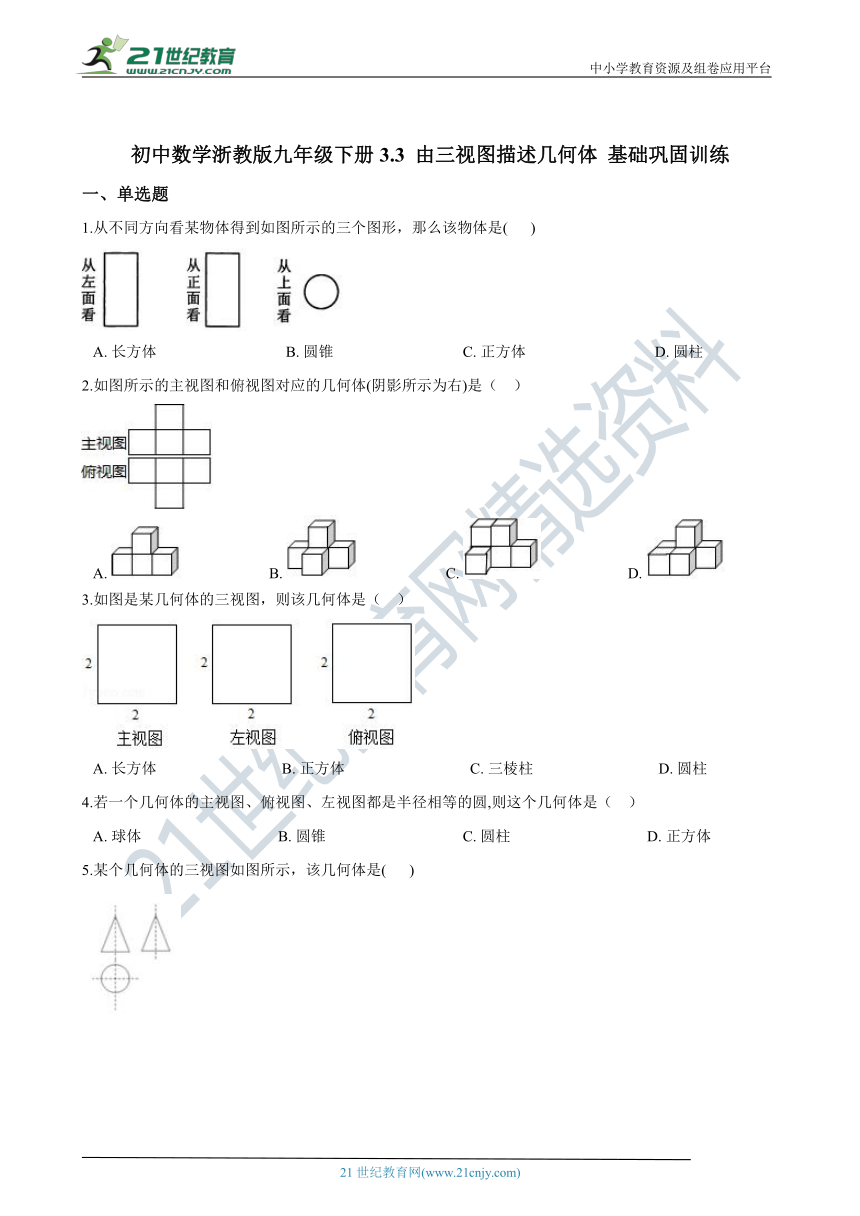 | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 17:50:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学浙教版九年级下册3.3 由三视图描述几何体 基础巩固训练
一、单选题
1.从不同方向看某物体得到如图所示的三个图形,那么该物体是(???? )
A.?长方体??????????????????????????????????B.?圆锥??????????????????????????????????C.?正方体??????????????????????????????????D.?圆柱
2.如图所示的主视图和俯视图对应的几何体(阴影所示为右)是(?? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
3.如图是某几何体的三视图,则该几何体是(?? )
A.?长方体?????????????????????????????????B.?正方体?????????????????????????????????C.?三棱柱?????????????????????????????????D.?圆柱
4.若一个几何体的主视图、俯视图、左视图都是半径相等的圆,则这个几何体是( ??)
A.?球体????????????????????????????????????B.?圆锥????????????????????????????????????C.?圆柱????????????????????????????????????D.?正方体
5.某个几何体的三视图如图所示,该几何体是(???? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
6.其几何体的三视图如图所示,这个几何体是( ??)
A.?三棱柱?????????????????????????????????B.?四棱锥?????????????????????????????????C.?四棱柱?????????????????????????????????D.?圆锥
7.与如图所示的三视图对应的几何体是( ??)
A.????????????????B.????????????????C.????????????????D.?
8.已知某几何体的三视图如图所示,那么这个几何体是(?? )
A.?长方体?????????????????????????????????B.?圆柱?????????????????????????????????C.?四棱锥?????????????????????????????????D.?四棱台
9.一个几何体的三视图如图所示,则这个几何体是( ??)
A.??????????????????B.??????????????????C.??????????????????D.?
10.已知某物体的三视图如图所示,那么与它对应的物体是
A.???????????????????????B.???????????????????????C.???????????????????????D.?
二、填空题
11.根据下列物体的三视图,填出几何体名称:该几何体是________.
12.一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米),这个零件的体积为________立方厘米。 21教育网
13.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是________cm2.
14.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的体积为________.
15.桌面上放两件物体,它们的三视图图,则这两个物体分别是________,它们的位置是________.
三、解答题
16.已知某几何体的三视图如图所示,其俯视图为等边三角形,求该几何体左视图的面积.
四、综合题
17.有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.
答案解析部分
一、单选题
1. D
解:∵主视图和左视图都是长方形,
∴此几何体为柱体,
∵俯视图是一个圆,
∴此几何体为圆柱,
故答案为:D.
分析:由主视图和左视图可得此几何体为柱体,根据俯视图是圆可判断出此几何体为圆柱.
2. B
解:A、B、D选项的主视图符合题意;
B选项的俯视图符合题意,
综上:对应的几何体为B选项中的几何体.
故答案为:B.
分析:主视图就是从前向后看得到的正投影,俯视图就是从上向下看得到的正投影,从而即可一一判断得出答案.21世纪教育网版权所有
3. B
解:由已知三视图得到几何体是以正方体。
故答案为:B。
分析:长方体的三视图应该是长_?????????é????????_、长方形或长方形、长方形、正方形;正方体的三视图都是正方形;三棱柱的三视图应该是长方形、长方形、三角形;圆柱的三视图应该是长方形、长方形、圆,综上所述即可一一判断得出答案。21cnjy.com
4. A
解:主视图、俯视图、左视图都是圆的几何体是球体.
故答案为:A.
分析:利用三视图都是圆,可得出几何体的形状.
5. D
由三视图可知:该几何体为圆锥.
故答案为:D.
分析:分别分析各个选项的三视图,据此判断即可.
6. B
解:∵空间几何体的主视图、左视图所对应的三角形皆为正三角形,俯视图对应的四边形为正方形,
∴空间几何体是正四棱锥,
故答案为:B.
分析:由空间几何体的主视图、左视图所对应的三角形皆为正三角形,俯视图对应的四边形为正方形,知空间几何体是正四棱锥.2·1·c·n·j·y
7. C
解:观察_???????????????A_、B、D的主视图不符合题意;
故答案为:C
分析:观察几何体的三视图,利用排除法,由主视图,排除A、B、D,即可得出正确答案。
8. A
因为_???è§?????????§è§?_图都是长方形,俯视图是正方形,所以此几何体是长方体;故答案为:A.
分析:根据主视图和侧视图都是长方形确定这个几何体是柱体,再根据俯视图是正方形确定这个几何体是四棱柱,据此判断即可.【来源:21·世纪·教育·网】
9. C
解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是三棱柱.
故答案为:C.
分析:由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状
10. B
解:从三视图可得此物体是圆柱体,从俯视图可知底面圆的直径是和长方体的宽相等的圆柱体.www-2-1-cnjy-com
故答案为:B.
分析:从俯视图可知底面圆的直径是和长方体宽相等的圆柱体,由此得出答案.
二、填空题
11. 六棱柱
解:通过俯视图可以判断出几何体的顶面是正六边形,然后根据主视图上中间有两条竖线,左视图中间有一条竖线,说明是六棱柱。 2-1-c-n-j-y
分析:由俯视图入手,先找到图形的主要特征,然后根据其他视图一起确定几何体名称。
12. 1800
解:由题意得,这个零件是长方体,且长为10,宽为12,高为15,
体积为
分析:根据三视图判定零件的形状,确定是长方体。主视图可以判定长方体的长和高,左视图判定长方体的宽和高。既而可求长方体的长宽高。【来源:21cnj*y.co*m】
13. 6
一个长方体的主视图和左视图如图所示,这个长方体的高是4,底面长是3,底面宽是2;长方体的俯视图就是其底面的图形,是长是3,宽是2的长方形,它的面积= =6
分析:先根据长方体的主视图和左视图确定出长方体的长、宽、高, 再根据其俯视图是长是3,宽是2的长方形即可求出答案.21*cnjy*com
14. 12
解:设俯视图的正方形的边长为a.
∵其俯视图为正方形,正方形的对角线长为2 ,
∴a2+a2=(2 )2 ,
解得a2=4,
∴这个长方体的体积为4×3=12.
分析:根据长方体的三视图可知,该长方体的俯视图是一个正方形,其对角线长,根据勾股定理计算出该长方体底面的长,与宽,又该长方体的高是3,根据长方体的体积计算公式即可算出答案。
15. 长方体和圆柱;圆柱在前,长方体在后
解:由三个视图可以判定这两件物体一个是圆柱,一个长方体;
由俯视图可以判定圆柱在前,长方体在后;
故答案为:长方体和圆柱;圆柱在前,长方体在后
分析:根据_???è§??????¤??????_何体,由三个视图可以判定这两件物体一个是圆柱,一个长方体;由俯视图可以判定圆柱在前,长方体在后;还可由左视图可以判定圆柱直立,长方体平放.【出处:21教育名师】
三、解答题
16. 解:由三视图可知,该几何体是一个三棱柱,且它的底面是边长为 ,高为 的等边三角形,它的高为 . 【版权所有:21教育】
所以该几何体左视图的面积为
.
分析:根据三视图的“长对正,高平齐,宽相等”判断及计算即可.
四、综合题
17. (1)解:如图:
(2)解:由勾股定理得:斜边长为10厘米,
S底= ×8×6=24(平方厘米),
S侧=(8+6+10)×3=72(平方厘米),
S全=72+24×2=120(平方厘米).
答:这个几何体的全面积是120平方厘米
分析:(1)_è§????????????????_,俯视图是一个长8宽3的长方形,据此画出图形即可;(2)先根据勾股定理得到斜边长为10厘米,再根据表面积=3个长方形的面积+2个三角形的面积,列出算式计算即可求解.www.21-cn-jy.com
_21?????????è?????(www.21cnjy.com)_
初中数学浙教版九年级下册3.3 由三视图描述几何体 基础巩固训练
一、单选题
1.从不同方向看某物体得到如图所示的三个图形,那么该物体是(???? )
A.?长方体??????????????????????????????????B.?圆锥??????????????????????????????????C.?正方体??????????????????????????????????D.?圆柱
2.如图所示的主视图和俯视图对应的几何体(阴影所示为右)是(?? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
3.如图是某几何体的三视图,则该几何体是(?? )
A.?长方体?????????????????????????????????B.?正方体?????????????????????????????????C.?三棱柱?????????????????????????????????D.?圆柱
4.若一个几何体的主视图、俯视图、左视图都是半径相等的圆,则这个几何体是( ??)
A.?球体????????????????????????????????????B.?圆锥????????????????????????????????????C.?圆柱????????????????????????????????????D.?正方体
5.某个几何体的三视图如图所示,该几何体是(???? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
6.其几何体的三视图如图所示,这个几何体是( ??)
A.?三棱柱?????????????????????????????????B.?四棱锥?????????????????????????????????C.?四棱柱?????????????????????????????????D.?圆锥
7.与如图所示的三视图对应的几何体是( ??)
A.????????????????B.????????????????C.????????????????D.?
8.已知某几何体的三视图如图所示,那么这个几何体是(?? )
A.?长方体?????????????????????????????????B.?圆柱?????????????????????????????????C.?四棱锥?????????????????????????????????D.?四棱台
9.一个几何体的三视图如图所示,则这个几何体是( ??)
A.??????????????????B.??????????????????C.??????????????????D.?
10.已知某物体的三视图如图所示,那么与它对应的物体是
A.???????????????????????B.???????????????????????C.???????????????????????D.?
二、填空题
11.根据下列物体的三视图,填出几何体名称:该几何体是________.
12.一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米),这个零件的体积为________立方厘米。 21教育网
13.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是________cm2.
14.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的体积为________.
15.桌面上放两件物体,它们的三视图图,则这两个物体分别是________,它们的位置是________.
三、解答题
16.已知某几何体的三视图如图所示,其俯视图为等边三角形,求该几何体左视图的面积.
四、综合题
17.有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.
答案解析部分
一、单选题
1. D
解:∵主视图和左视图都是长方形,
∴此几何体为柱体,
∵俯视图是一个圆,
∴此几何体为圆柱,
故答案为:D.
分析:由主视图和左视图可得此几何体为柱体,根据俯视图是圆可判断出此几何体为圆柱.
2. B
解:A、B、D选项的主视图符合题意;
B选项的俯视图符合题意,
综上:对应的几何体为B选项中的几何体.
故答案为:B.
分析:主视图就是从前向后看得到的正投影,俯视图就是从上向下看得到的正投影,从而即可一一判断得出答案.21世纪教育网版权所有
3. B
解:由已知三视图得到几何体是以正方体。
故答案为:B。
分析:长方体的三视图应该是长_?????????é????????_、长方形或长方形、长方形、正方形;正方体的三视图都是正方形;三棱柱的三视图应该是长方形、长方形、三角形;圆柱的三视图应该是长方形、长方形、圆,综上所述即可一一判断得出答案。21cnjy.com
4. A
解:主视图、俯视图、左视图都是圆的几何体是球体.
故答案为:A.
分析:利用三视图都是圆,可得出几何体的形状.
5. D
由三视图可知:该几何体为圆锥.
故答案为:D.
分析:分别分析各个选项的三视图,据此判断即可.
6. B
解:∵空间几何体的主视图、左视图所对应的三角形皆为正三角形,俯视图对应的四边形为正方形,
∴空间几何体是正四棱锥,
故答案为:B.
分析:由空间几何体的主视图、左视图所对应的三角形皆为正三角形,俯视图对应的四边形为正方形,知空间几何体是正四棱锥.2·1·c·n·j·y
7. C
解:观察_???????????????A_、B、D的主视图不符合题意;
故答案为:C
分析:观察几何体的三视图,利用排除法,由主视图,排除A、B、D,即可得出正确答案。
8. A
因为_???è§?????????§è§?_图都是长方形,俯视图是正方形,所以此几何体是长方体;故答案为:A.
分析:根据主视图和侧视图都是长方形确定这个几何体是柱体,再根据俯视图是正方形确定这个几何体是四棱柱,据此判断即可.【来源:21·世纪·教育·网】
9. C
解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是三棱柱.
故答案为:C.
分析:由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状
10. B
解:从三视图可得此物体是圆柱体,从俯视图可知底面圆的直径是和长方体的宽相等的圆柱体.www-2-1-cnjy-com
故答案为:B.
分析:从俯视图可知底面圆的直径是和长方体宽相等的圆柱体,由此得出答案.
二、填空题
11. 六棱柱
解:通过俯视图可以判断出几何体的顶面是正六边形,然后根据主视图上中间有两条竖线,左视图中间有一条竖线,说明是六棱柱。 2-1-c-n-j-y
分析:由俯视图入手,先找到图形的主要特征,然后根据其他视图一起确定几何体名称。
12. 1800
解:由题意得,这个零件是长方体,且长为10,宽为12,高为15,
体积为
分析:根据三视图判定零件的形状,确定是长方体。主视图可以判定长方体的长和高,左视图判定长方体的宽和高。既而可求长方体的长宽高。【来源:21cnj*y.co*m】
13. 6
一个长方体的主视图和左视图如图所示,这个长方体的高是4,底面长是3,底面宽是2;长方体的俯视图就是其底面的图形,是长是3,宽是2的长方形,它的面积= =6
分析:先根据长方体的主视图和左视图确定出长方体的长、宽、高, 再根据其俯视图是长是3,宽是2的长方形即可求出答案.21*cnjy*com
14. 12
解:设俯视图的正方形的边长为a.
∵其俯视图为正方形,正方形的对角线长为2 ,
∴a2+a2=(2 )2 ,
解得a2=4,
∴这个长方体的体积为4×3=12.
分析:根据长方体的三视图可知,该长方体的俯视图是一个正方形,其对角线长,根据勾股定理计算出该长方体底面的长,与宽,又该长方体的高是3,根据长方体的体积计算公式即可算出答案。
15. 长方体和圆柱;圆柱在前,长方体在后
解:由三个视图可以判定这两件物体一个是圆柱,一个长方体;
由俯视图可以判定圆柱在前,长方体在后;
故答案为:长方体和圆柱;圆柱在前,长方体在后
分析:根据_???è§??????¤??????_何体,由三个视图可以判定这两件物体一个是圆柱,一个长方体;由俯视图可以判定圆柱在前,长方体在后;还可由左视图可以判定圆柱直立,长方体平放.【出处:21教育名师】
三、解答题
16. 解:由三视图可知,该几何体是一个三棱柱,且它的底面是边长为 ,高为 的等边三角形,它的高为 . 【版权所有:21教育】
所以该几何体左视图的面积为
.
分析:根据三视图的“长对正,高平齐,宽相等”判断及计算即可.
四、综合题
17. (1)解:如图:
(2)解:由勾股定理得:斜边长为10厘米,
S底= ×8×6=24(平方厘米),
S侧=(8+6+10)×3=72(平方厘米),
S全=72+24×2=120(平方厘米).
答:这个几何体的全面积是120平方厘米
分析:(1)_è§????????????????_,俯视图是一个长8宽3的长方形,据此画出图形即可;(2)先根据勾股定理得到斜边长为10厘米,再根据表面积=3个长方形的面积+2个三角形的面积,列出算式计算即可求解.www.21-cn-jy.com
_21?????????è?????(www.21cnjy.com)_
