浙教版八年级下册数学4.1多边形(2)课件(共19张)
文档属性
| 名称 | 浙教版八年级下册数学4.1多边形(2)课件(共19张) |  | |
| 格式 | zip | ||
| 文件大小 | 702.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 12:07:53 | ||
图片预览




文档简介
(共19张PPT)
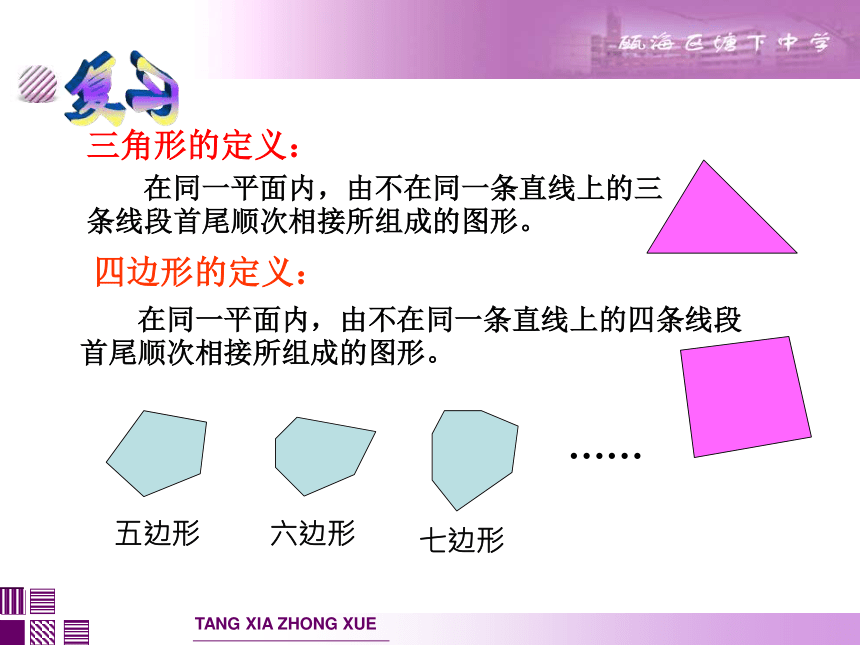
三角形的定义:
在同一平面内,由不在同一条直线上的三条线段首尾顺次相接所组成的图形。
四边形的定义:
在同一平面内,由不在同一条直线上的四条线段首尾顺次相接所组成的图形。
……
五边形
六边形
七边形
多边形的定义:
在同一平面内,由不在同一条直线上的一些线段首尾顺次相接所组成的(封闭)图形。
多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形。
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。
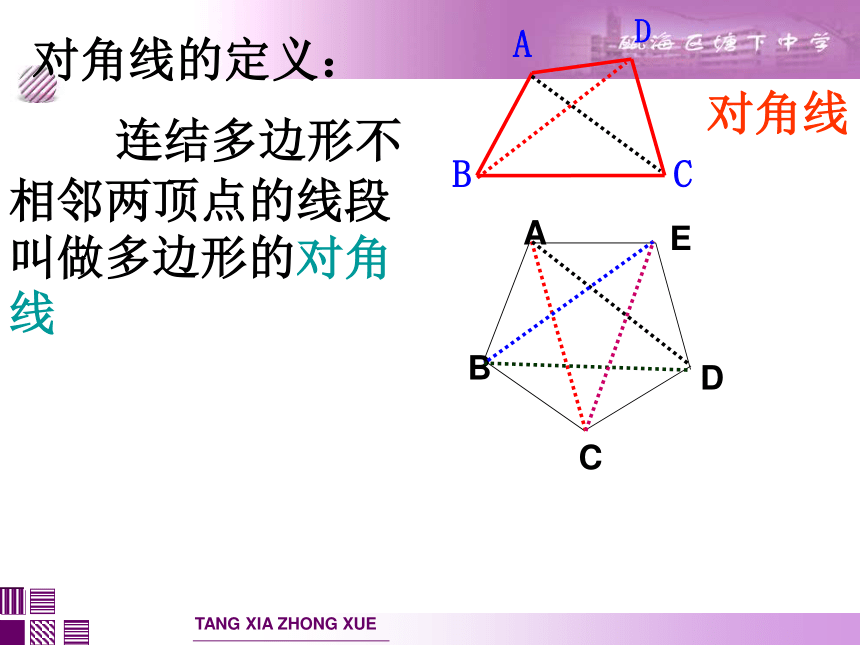
连结多边形不相邻两顶点的线段叫做多边形的对角线
对角线的定义:
对角线
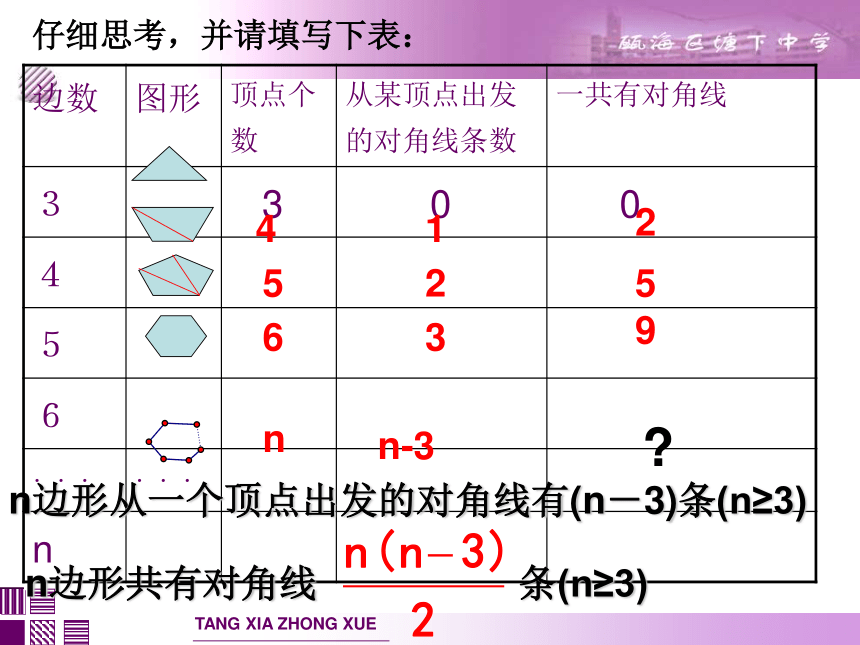
仔细思考,并请填写下表:
n
5
6
4
1
2
3
n-3
2
5
9
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
?
边数 图形 顶点个数 从某顶点出发的对角线条数 一共有对角线
3 3 0 0
4
5
6
... ...
n
三角形
六边形
四边形
八边形
……..
五边形
从某一个顶点出发画对角线
多边形问题 三角形问题
转化
(未知)
(已知)
你能求出图中五边形的五个内角和吗?
五边形的内角和为:540°
多边形问题 三角形问题
转化
(未知)
(已知)
请探索任意一个多边形的内角和与外角和的规律.
合作交流,探究新知 :
仔细思考,并请填写下表:
2
3
3
4
3×180°
4×180°
n- 3
n- 2
(n-2)×180°
边数 图形 从某顶点出发的对角线条数 划分成的三角形个数 多边形的内角和
3 0 1 1×180°
4 1 2 2×180°
5
6
... ...
n
结论:n边形的内角和为:
(n-2)×180°(n≥3).
思考:n边形的外角和又是多少
度呢?
3×180o-1×180o=360o
4×180o-2×180o=360o
5×180o-3×180o=360o
6×180o-4×180o=360o
n×180o-(n-2)×180o=360o
多边形的外角和
结论:任何多边形的外角和为360°
多边形 图形 多边形的外角和
三角形
四边形
五边形
六边形
n边形
练一练:
(2)已知一个多边形的内角和为900o ,则这个多边形是______边形
7
(1)十边形的内角和为______,外角和为_____
1440o
360o
(3)已知一个多边形的每一个外角都是72o,求这个边形的边数为______
(4)一个多边形的内角和等于它的外角和的3倍,它是几边形?
5
八边形
∵AB∥DE, CD∥AF(已知)
∴∠1=∠3,∠2=∠4(两 直线平行,内错角相等)
∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F
∴∠FAB+∠C+∠E= 1/2 ×720°=360°
思考:有没有其它的解法?
∵∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠AFE=(6-2)×180°=720°
∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1=∠2,
∴∠CDE=∠FAB
同理∠AFE=∠BCD,∠ABC=∠DEF
∴∠FAB+∠BCD+∠DEF= 1/2 ×720°=360°
已知AB∥DE,BC∥EF,CD∥AF,求∠A+∠C+∠E的度数。
(1)一个多边形中,锐角最多
只能有三个。( )
思考:
(2)n边形的每个内角都等于120°,
则n=?
(3)一个内角和为1620°的多边
形有多少条对角线?
n边形的内角和为(n-2) ×180°(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
任何多边形的外角和为360°
多边形问题 三角形问题
转化
三角形的定义:
在同一平面内,由不在同一条直线上的三条线段首尾顺次相接所组成的图形。
四边形的定义:
在同一平面内,由不在同一条直线上的四条线段首尾顺次相接所组成的图形。
……
五边形
六边形
七边形
多边形的定义:
在同一平面内,由不在同一条直线上的一些线段首尾顺次相接所组成的(封闭)图形。
多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形。
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。
连结多边形不相邻两顶点的线段叫做多边形的对角线
对角线的定义:
对角线
仔细思考,并请填写下表:
n
5
6
4
1
2
3
n-3
2
5
9
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
?
边数 图形 顶点个数 从某顶点出发的对角线条数 一共有对角线
3 3 0 0
4
5
6
... ...
n
三角形
六边形
四边形
八边形
……..
五边形
从某一个顶点出发画对角线
多边形问题 三角形问题
转化
(未知)
(已知)
你能求出图中五边形的五个内角和吗?
五边形的内角和为:540°
多边形问题 三角形问题
转化
(未知)
(已知)
请探索任意一个多边形的内角和与外角和的规律.
合作交流,探究新知 :
仔细思考,并请填写下表:
2
3
3
4
3×180°
4×180°
n- 3
n- 2
(n-2)×180°
边数 图形 从某顶点出发的对角线条数 划分成的三角形个数 多边形的内角和
3 0 1 1×180°
4 1 2 2×180°
5
6
... ...
n
结论:n边形的内角和为:
(n-2)×180°(n≥3).
思考:n边形的外角和又是多少
度呢?
3×180o-1×180o=360o
4×180o-2×180o=360o
5×180o-3×180o=360o
6×180o-4×180o=360o
n×180o-(n-2)×180o=360o
多边形的外角和
结论:任何多边形的外角和为360°
多边形 图形 多边形的外角和
三角形
四边形
五边形
六边形
n边形
练一练:
(2)已知一个多边形的内角和为900o ,则这个多边形是______边形
7
(1)十边形的内角和为______,外角和为_____
1440o
360o
(3)已知一个多边形的每一个外角都是72o,求这个边形的边数为______
(4)一个多边形的内角和等于它的外角和的3倍,它是几边形?
5
八边形
∵AB∥DE, CD∥AF(已知)
∴∠1=∠3,∠2=∠4(两 直线平行,内错角相等)
∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F
∴∠FAB+∠C+∠E= 1/2 ×720°=360°
思考:有没有其它的解法?
∵∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠AFE=(6-2)×180°=720°
∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1=∠2,
∴∠CDE=∠FAB
同理∠AFE=∠BCD,∠ABC=∠DEF
∴∠FAB+∠BCD+∠DEF= 1/2 ×720°=360°
已知AB∥DE,BC∥EF,CD∥AF,求∠A+∠C+∠E的度数。
(1)一个多边形中,锐角最多
只能有三个。( )
思考:
(2)n边形的每个内角都等于120°,
则n=?
(3)一个内角和为1620°的多边
形有多少条对角线?
n边形的内角和为(n-2) ×180°(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
任何多边形的外角和为360°
多边形问题 三角形问题
转化
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
