浙教版八年级数学下册第四章平行四边形全章复习与巩固(提高)巩固练习含答案
文档属性
| 名称 | 浙教版八年级数学下册第四章平行四边形全章复习与巩固(提高)巩固练习含答案 | 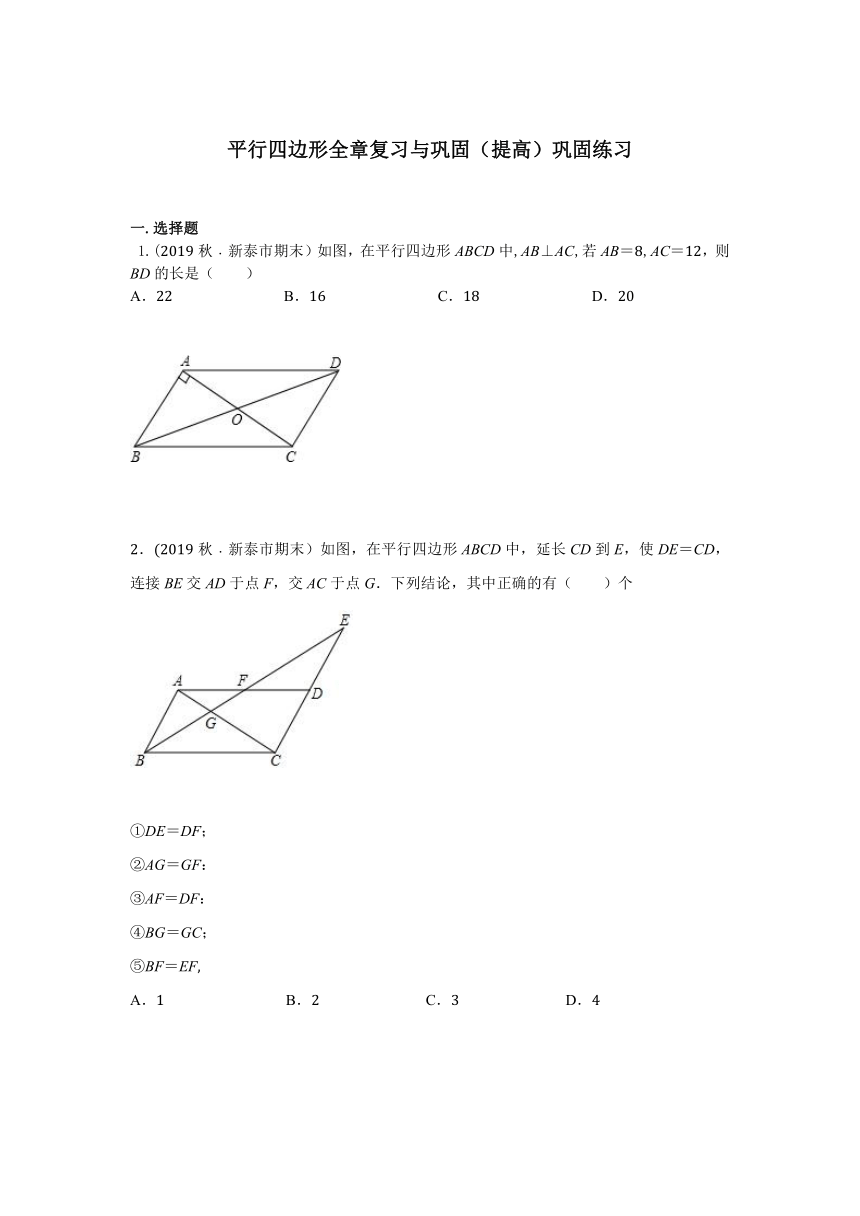 | |
| 格式 | zip | ||
| 文件大小 | 131.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 12:56:06 | ||
图片预览




文档简介
平行四边形全章复习与巩固(提高)巩固练习
一.选择题
1.(2019秋﹒新泰市期末)如图,在平行四边形ABCD中,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.22 B.16 C.18 D.20
2.(2019秋﹒新泰市期末)如图,在平行四边形ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.下列结论,其中正确的有( )个
①DE=DF;
②AG=GF:
③AF=DF:
④BG=GC;
⑤BF=EF,
A.1 B.2 C.3 D.4
3.(2019秋﹒温岭市期末)多边形每一个内角都等于150°,则从该多边形一个顶点出发,可引出对角线的条数为( )
A.6条 B.8条 C.9条 D.12条
4. 对于命题“如果<<0,那么> .”用反证法证明,应假设( )
A. > B. < C. ≥ D. ≤
5.平行四边形的一边长是10cm,那么这个平行四边形的两条对角线的长可以是( )
A.4cm和6cm B.6cm和8cm C.8cm和10cm D.10cm和12cm
6.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( )
A. B. C.4 D.8
7.(2019春?嵊州市校级期中)如图,△ABC的周长为26,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长是( )
A.1.5 B.2 C.3 D.4
8.(2019春?定州市期中)如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=5,BC=6,OE=2,那么四边形EFCD周长是( )
A.16 B.15 C.14 D.13
二.填空题
9. (2019秋﹒乳山市期末)如图,在□ABCD中,MN过点D,与BA,BC的延长线交于M,N,∠NDC=∠MDA,BM=6,则□ABCD的周长为 .
10.已知任意直线l把口ABCD分成两部分,要使这两部分的面积相等,直线l所在位置需满足的条件是________.
11.已知点A、B关于x轴上的点P(-1,0)成中心对称,若点A的坐标为(1,2),则点B坐标是_______.
12. 如图所示,在口ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N.给出下列结论:①△ABM≌△CDN;②AM=AC;③DN=2NF;④.其中正确的结论是________.(只填序号)
13.如图,口ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=________厘米.
14.如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=_____度.
15.(2019?朝阳区二模)如果一个平行四边形一个内角的平分线分它的一边为1:2的两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”.当“协调边”为3时,它的周长为 .
16.(2019秋﹒诸城市期末)如图,在四边形ABCD中,AD∥BC,AD=5,BC=18,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动,当运动时间t秒时,以点P,Q,E,D为顶点的四边形是平行四边形,则t的值为 .
三.解答题
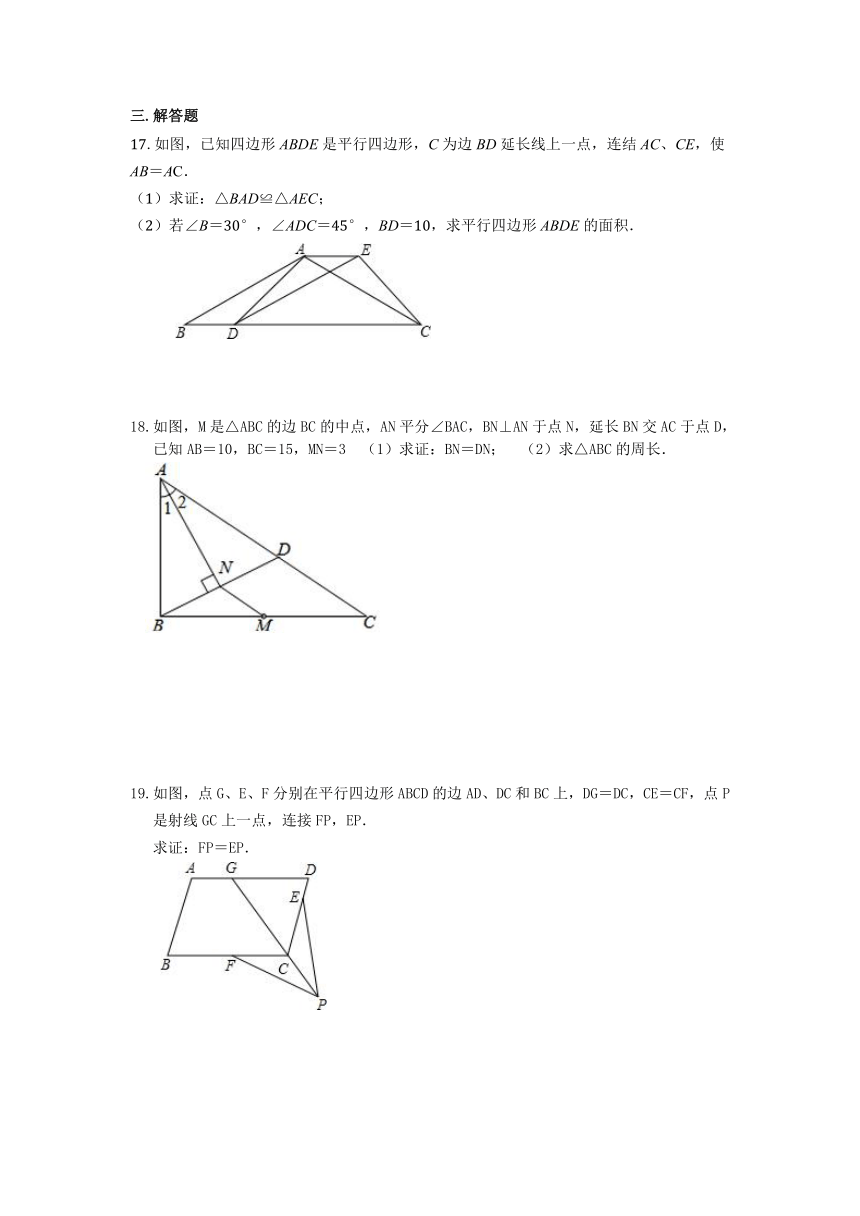
17.如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.
(1)求证:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
18.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3?(1)求证:BN=DN;?(2)求△ABC的周长.?
?
19.如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP.
求证:FP=EP.
20.(2019?海淀区二模)如图1,在△ABC中,AB=AC,∠ABC=α,D是BC边上一点,以AD为边作△ADE,使AE=AD,∠DAE+∠BAC=180°.
(1)直接写出∠ADE的度数(用含α的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
【答案与解析】
一.选择题
1.【答案】D;
2.【答案】B;
3.【答案】C;
4.【答案】D;
【解析】由于结论>的否定为:≤ ,故应假设≤ ,由此推出矛盾.
5.【答案】D;
6.【答案】B;
7.【答案】C;
【解析】解:∵BQ平分∠ABC,BQ⊥AE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点Q是AE中点,点P是AD中点(三线合一),
∴PQ是△ADE的中位线,
∵BE+CD=AB+AC=26﹣BC=26﹣10=16,
∴DE=BE+CD﹣BC=6,
∴PQ=DE=3.
故选:C.
8.【答案】B;
【解析】解:∵四边形ABCD是平行四边形,
∴AD=BC=6,AB=CD=5,OA=OC,AD∥BC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(ASA),
∴AE=CF,OE=OF=2,
∴DE+CF=DE+AE=AD=6,
∴四边形EFCD的周长是EF+FC+CD+DE=2+2+6+5=15,
故选B.
二.填空题
9.【答案】12.
10.【答案】经过对角线的交点;
【解析】由于平行四边形是中心对称图形,对称中心为对角线的交点,因而过对角线的交点的直线就能把平行四边形分成全等的两部分,这两部分的面积也就相等了.
11.【答案】(-3,-2);
【解析】根据对称中心与两点的关系列式计算即可得解.
12.【答案】①②③;
【解析】易证四边形BEDF是平行四边形,△ABM≌△CDN.∴ ①正确.
由口BEDF可得∠BED=∠BFD,∴∠AEM=∠NFC.又∵AD∥BC.∴∠EAM=∠NCF, 又AE=CF∴ △AME≌△CNF,∴AM=CN.由FN∥BM,FC=BF,得CN=MN,∴CN=MN=AM,AM=AC.∴ ②正确.
∵ AM=AC,∴ ,∴④不正确.
FN为△BMC的中位线,BM=2NF,△ABM≌△CDN,则BM=DN,∴DN=2NF,
∴③正确.
13.【答案】3;
【解析】根据AC+BD=24厘米,可得出出OA+OB=12cm,继而求出AB,判断EF是△OAB的中位线即可得出EF的长度.
14.【答案】105;
【解析】∵平行四边形ABCD绕点A逆时针旋转30°,∴AB=AB′,∠BAB′=30°,∴∠B=∠AB′B=(180°-30°)÷2=75°,∴∠C=180°-75°=105°.
15.【答案】8或10.
【解析】解:如图所示:①当AE=1,DE=2时,
∵四边形ABCD是平行四边形,
∴BC=AD=3,AB=CD,AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE=1,
∴平行四边形ABCD的周长=2(AB+AD)=8;
②当AE=2,DE=1时,
同理得:AB=AE=2,
∴平行四边形ABCD的周长=2(AB+AD)=10;
故答案为:8或10.
16.【答案】2秒或3.5秒;
三.解答题
17.【解析】
(1)证明:∵AB=AC,
∴∠B=∠ACB.
又∵四边形ABDE是平行四边形
∴AE∥BD,AE=BD,
∴∠ACB=∠CAE=∠B,
在△DBA和△AEC中
,
∴△DBA≌△AEC(SAS);
(2)解:过A作AG⊥BC,垂足为G.设AG=x,
在Rt△AGD中,∵∠ADC=45°,
∴AG=DG=x,
在Rt△AGB中,∵∠B=30°,
∴BG=x,
又∵BD=10.
∴BG-DG=BD,即x?x=10,
解得AG=x==5+5,
∴=BD?AG=10×(5+5)=50+50.
18.【解析】
(1)证明:在△ABN和△ADN中,
∵
∴△ABN≌△ADN,?∴BN=DN.?
(2)解:∵△ABN≌△ADN,
?∴AD=AB=10,DN=NB,?
又∵点M是BC中点,
∴MN是△BDC的中位线,
∴CD=2MN=6,?
故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.?
19.【解析】
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DGC=∠GCB(两直线平行,内错角相等),
∵DG=DC,
∴∠DGC=∠DCG,
∴∠DCG=∠GCB,
∵∠DCG+∠DCP=180°,∠GCB+∠FCP=180°,
∴∠DCP=∠FCP,
∵在△PCF和△PCE中
,
∴△PCF≌△PCE(SAS),
∴PF=PE.
20.【解析】
解:(1)∵在△ABC中,AB=AC,∠ABC=α,
∴∠BAC=180°﹣2α,
∵∠DAE+∠BAC=180°,
∴∠DAE=2α,
∵AE=AD,
∴∠ADE=90°﹣α;
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥EF.
∴∠EDC=∠ABC=α,
由(1)知,∠ADE=90°﹣α,
∴∠ADC=∠ADE+∠EDC=90°,
∴AD⊥BC.
∵AB=AC,
∴BD=CD;
②证明:∵AB=AC,∠ABC=α,
∴∠C=∠B=α.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴∠EAC=∠C=α,
由(1)知,∠DAE=2α,
∴∠DAC=α,
∴∠DAC=∠C.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
