浙教版八年级下册5.1 矩形(提高)巩固练习含答案
文档属性
| 名称 | 浙教版八年级下册5.1 矩形(提高)巩固练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 160.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 10:43:43 | ||
图片预览

文档简介
矩形(提高)巩固练习
一.选择题
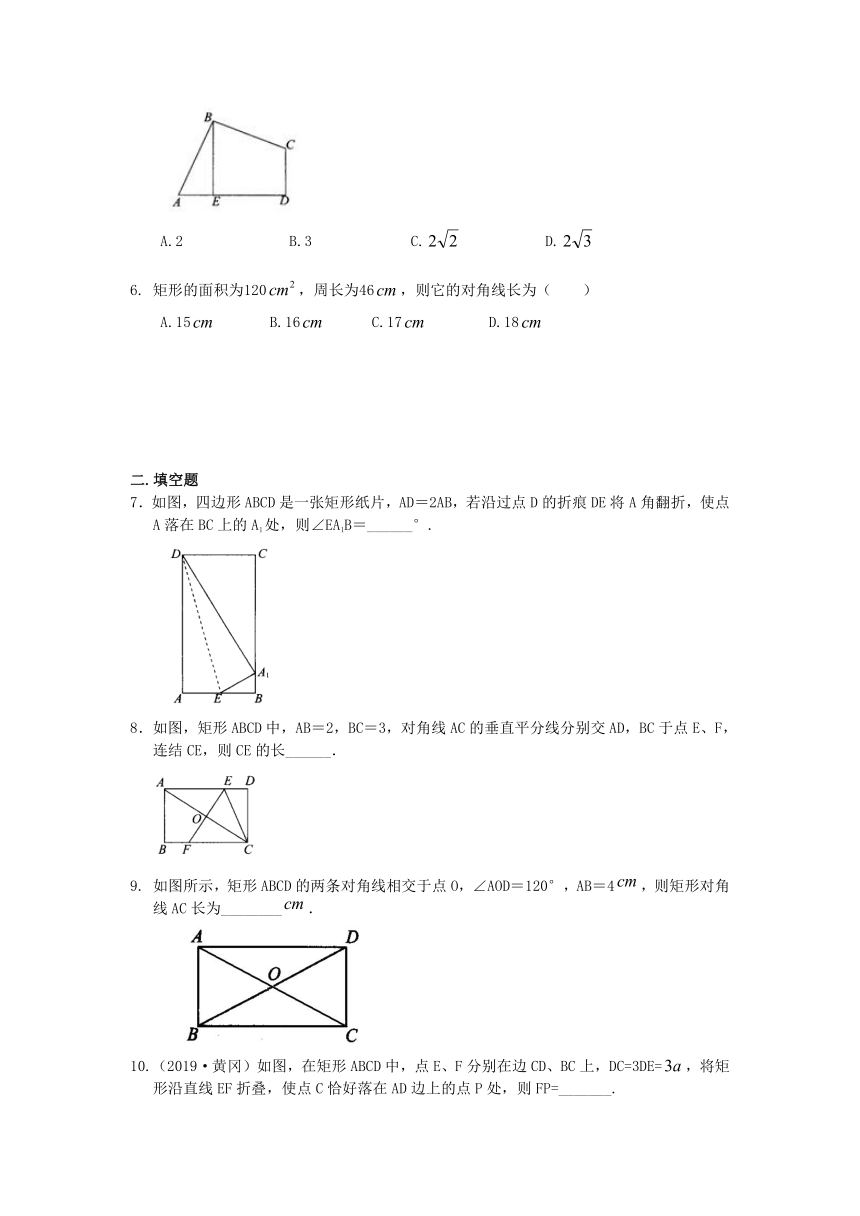
1. (2020﹒淮南模拟)在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形,等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上.这个等腰三角形剪法有( )
A.1 B.2 C.3 D.4
2. (2019秋﹒海港区期末)如图:用一张长为4cm,宽3cm的长方形纸片,过两个顶点剪一个三角形,按裁剪线长度所标的数据(单位:cm)不可能实现的是( )
A. B. C. D.
3.(2019春?青浦区期末)已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED,EC,AC,添加一个条件,能使四边形ACDE成为矩形的是( )
A.AC=CD B.AB=AD C.AD=AE D.BC=CE
4. 把一张长方形的纸片按如图所示的方式折叠,EM、FM为折痕,折叠后的C点落在B′M或B′M的延长线上,那么∠EMF的度数是( )
A.85° B.90° C.95° D.100°
5.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( )
A.2 B.3 C. D.
6. 矩形的面积为120,周长为46,则它的对角线长为( )
A.15 B.16 C.17 D.18
二.填空题
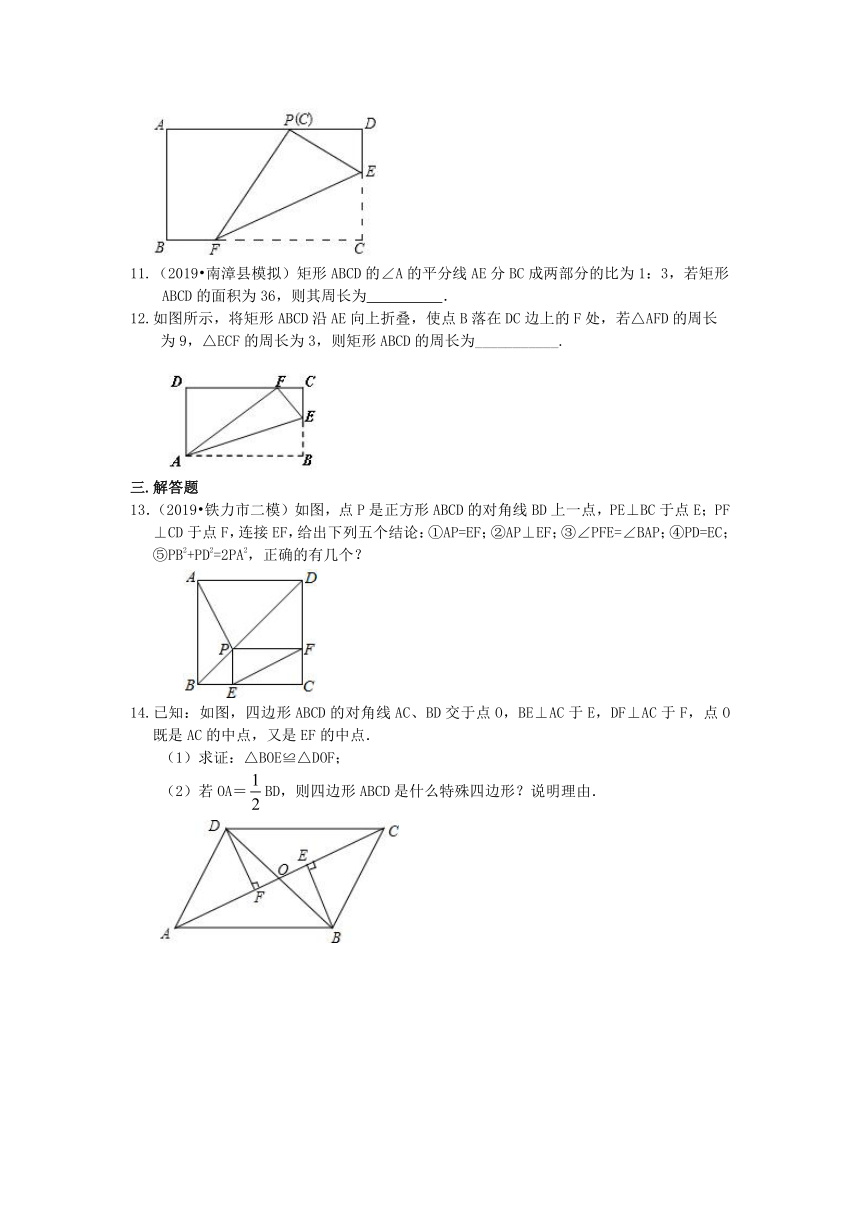
7.如图,四边形ABCD是一张矩形纸片,AD=2AB,若沿过点D的折痕DE将A角翻折,使点A落在BC上的A1处,则∠EA1B=______°.
8.如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F,连结CE,则CE的长______.
9. 如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=4,则矩形对角线AC长为________.
10.(2019·黄冈)如图,在矩形ABCD中,点E、F分别在边CD、BC上,DC=3DE=,将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=_______.
11.(2019?南漳县模拟)矩形ABCD的∠A的平分线AE分BC成两部分的比为1:3,若矩形ABCD的面积为36,则其周长为 .
12.如图所示,将矩形ABCD沿AE向上折叠,使点B落在DC边上的F处,若△AFD的周长
为9,△ECF的周长为3,则矩形ABCD的周长为___________.
三.解答题
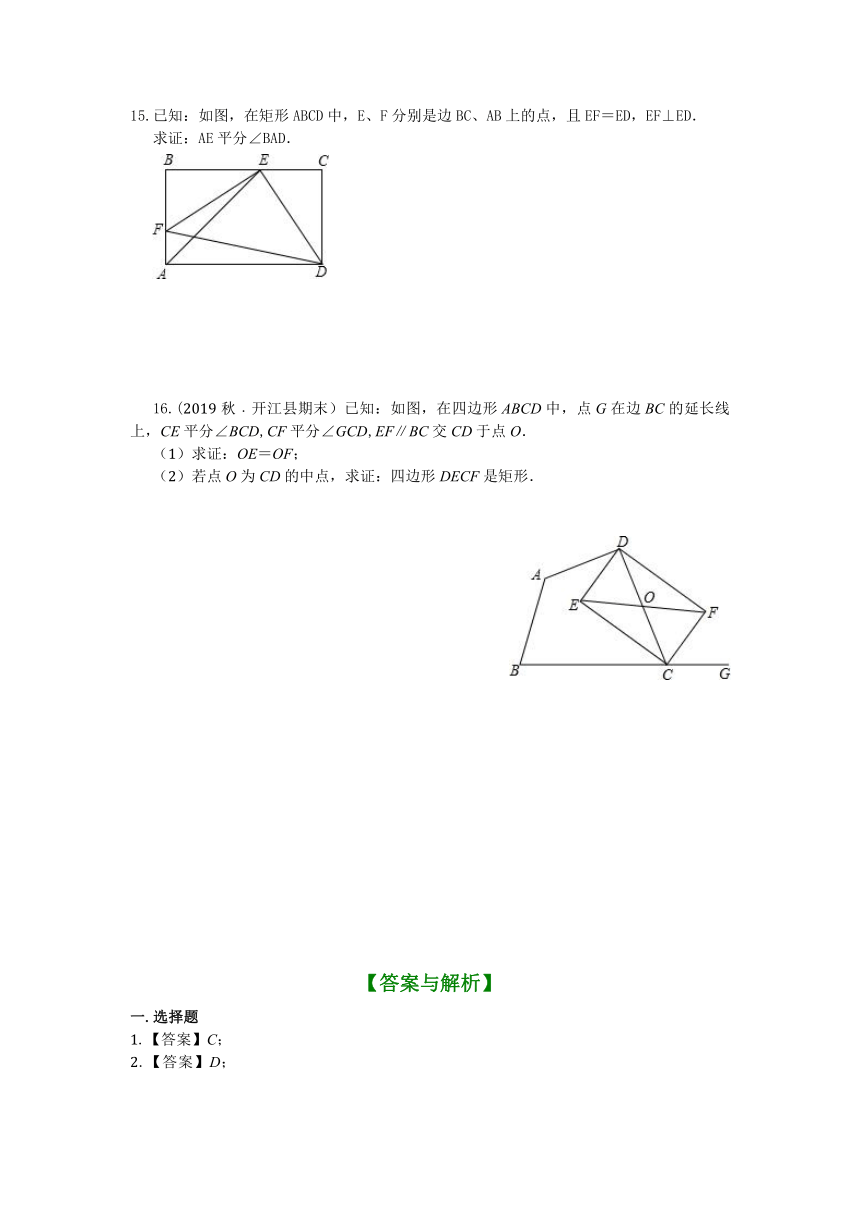
13.(2019?铁力市二模)如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有几个?
14.已知:如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?说明理由.
15.已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.
求证:AE平分∠BAD.
16.(2019秋﹒开江县期末)已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
【答案与解析】
一.选择题
1.【答案】C;
2.【答案】D;
3.【答案】D;
【解析】添加一个条件BC=CE.
理由:∵四边形ABCD为平行四边形,∴AB∥CD且AB=CD,
∵AE=AB,∴AE∥CD且AE=CD,∴四边形DEAC为平行四边形,
∵BC=EC,AE=AB,∴∠EAC=90°,∴平行四边形ACDE是矩形.
4.【答案】B;
【解析】∠EMF=∠EMB′+∠FMB′=∠BMC′+∠CMC′=×180°=90°.
5.【答案】C;
【解析】过点C做BE垂线,垂足为F,易证△BAE≌△CBF,所以BF=AE,BE=CF,所以总面积=AE×BE+CF×EF= AE×BE+BE×(BE-AE)=,.
6.【答案】C;
【解析】设边长为,则解得,所以对角线为.
二.填空题
7.【答案】60°;???
【解析】AD=A1D=2CD,所以∠CA1?D=30°,∠EA1B=60°.
8.【答案】;
【解析】设AE=CE=,DE=,,.
9.【答案】8;
【解析】由矩形的性质可知△AOB是等边三角形,∴ AC=2AO=2AB=8.
10.【答案】;
【解析】作FM⊥AD于M,如图所示:
则MF=DC=,由题意可得:CE=,
由折叠可得:PE=CE==2DE,∠EPF=∠C=90°,
∴∠DPE=30°,∴∠MPF=60°,∠MFP=30°,∴FP=.
11.【答案】30或10;
【解析】∵AE平分∠DAB,
∴∠DAE=∠EAB,
∵四边形ABCD是矩形,
∴AD=BC,DC=AB,AD∥BC,
∴∠DEA=∠BEA,
∴∠EAB=∠BEA,
∴AB=BE,
①设BE=x,CE=3x,则AD=4x,AB=x,
∵矩形ABCD的面积为36,
∴x?4x=36,
解得:x=3(舍负),
即AD=BC=4x=12,AB=CD=x=3,
∴矩形的周长为:AB+BC+CD+AD=2×(3+12)=30;
②设BE=3x,CE=x,则AD=4x,AB=3x,
∵矩形ABCD的面积为36,
∴3x?4x=36,
解得:x=(舍负),
即AD=BC=4x=4,AB=CD=x=,
∴矩形的周长为:AB+BC+CD+AD=2×(4+)=10;
故答案为:30或10.
12.【答案】12;
【解析】设BE=EF=,CE=,CF=,DF=,则,解得,矩形ABCD的周长=.
三.解答题
13.【解析】
解:①正确,连接PC,可得PC=EF,PC=PA,∴AP=EF;
②正确;延长AP,交EF于点N,则∠EPN=∠BAP=∠PCE=∠PFE,可得AP⊥EF;
③正确;∠PFE=∠PCE=∠BAP;
④错误,PD=PF=CE;
⑤正确,PB2+PD2=2PA2.
所以正确的有4个:①②③⑤.
14.【解析】
(1)证明:∵BE⊥AC.DF⊥AC,
∴∠BEO=∠DFO=90°,
∵点O是EF的中点,
∴OE=OF,
又∵∠DOF=∠BOE,
∴△BOE≌△DOF(ASA);
(2)解:四边形ABCD是矩形.理由如下:
∵△BOE≌△DOF,
∴OB=OD,
又∵OA=OC,
∴四边形ABCD是平行四边形,
∵OA=BD,OA=AC,
∴BD=AC,
∴ABCD是矩形.
15.【解析】
证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠BAD=90°,AB=CD,
∴∠BEF+∠BFE=90°.
∵EF⊥ED,
∴∠BEF+∠CED=90°.
∴∠BFE=∠CED.
又∵EF=ED,
∴△EBF≌△DCE.
∴BE=CD.
∴BE=AB.∴∠BAE=∠BEA=45°.
∴∠EAD=45°.
∴∠BAE=∠EAD.
∴AE平分∠BAD.
16.
【解答】证明:
(1)∵CE平分∠BCD、CF平分∠GCD,
∴∠BCE=∠DCE,∠DCF=∠GCF,
∵EF∥BC,
∴∠BCE=∠FEC,∠EFC=∠GCF,
∴∠DCE=∠FEC,∠EFC=∠DCF,
∴OE=OC,OF=OC,
∴OE=OF;
(2)∵点O为CD的中点,
∴OD=OC,
又OE=OF,
∴四边形DECF是平行四边形,
∵CE平分∠BCD、CF平分∠GCD,
∴∠DCE==
∴∠DCE+∠DCF==90°,
即∠ECF=90°,
∴四边形DECF是矩形.
【点评】本题主要考查平行线的性质及矩形的判定,证得OE=OF,得出四边形DECF是平行四边形是解题的关键,注意角平分线的应用.
PAGE
一.选择题
1. (2020﹒淮南模拟)在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形,等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上.这个等腰三角形剪法有( )
A.1 B.2 C.3 D.4
2. (2019秋﹒海港区期末)如图:用一张长为4cm,宽3cm的长方形纸片,过两个顶点剪一个三角形,按裁剪线长度所标的数据(单位:cm)不可能实现的是( )
A. B. C. D.
3.(2019春?青浦区期末)已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED,EC,AC,添加一个条件,能使四边形ACDE成为矩形的是( )
A.AC=CD B.AB=AD C.AD=AE D.BC=CE
4. 把一张长方形的纸片按如图所示的方式折叠,EM、FM为折痕,折叠后的C点落在B′M或B′M的延长线上,那么∠EMF的度数是( )
A.85° B.90° C.95° D.100°
5.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( )
A.2 B.3 C. D.
6. 矩形的面积为120,周长为46,则它的对角线长为( )
A.15 B.16 C.17 D.18
二.填空题
7.如图,四边形ABCD是一张矩形纸片,AD=2AB,若沿过点D的折痕DE将A角翻折,使点A落在BC上的A1处,则∠EA1B=______°.
8.如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F,连结CE,则CE的长______.
9. 如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=4,则矩形对角线AC长为________.
10.(2019·黄冈)如图,在矩形ABCD中,点E、F分别在边CD、BC上,DC=3DE=,将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=_______.
11.(2019?南漳县模拟)矩形ABCD的∠A的平分线AE分BC成两部分的比为1:3,若矩形ABCD的面积为36,则其周长为 .
12.如图所示,将矩形ABCD沿AE向上折叠,使点B落在DC边上的F处,若△AFD的周长
为9,△ECF的周长为3,则矩形ABCD的周长为___________.
三.解答题
13.(2019?铁力市二模)如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有几个?
14.已知:如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?说明理由.
15.已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.
求证:AE平分∠BAD.
16.(2019秋﹒开江县期末)已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
【答案与解析】
一.选择题
1.【答案】C;
2.【答案】D;
3.【答案】D;
【解析】添加一个条件BC=CE.
理由:∵四边形ABCD为平行四边形,∴AB∥CD且AB=CD,
∵AE=AB,∴AE∥CD且AE=CD,∴四边形DEAC为平行四边形,
∵BC=EC,AE=AB,∴∠EAC=90°,∴平行四边形ACDE是矩形.
4.【答案】B;
【解析】∠EMF=∠EMB′+∠FMB′=∠BMC′+∠CMC′=×180°=90°.
5.【答案】C;
【解析】过点C做BE垂线,垂足为F,易证△BAE≌△CBF,所以BF=AE,BE=CF,所以总面积=AE×BE+CF×EF= AE×BE+BE×(BE-AE)=,.
6.【答案】C;
【解析】设边长为,则解得,所以对角线为.
二.填空题
7.【答案】60°;???
【解析】AD=A1D=2CD,所以∠CA1?D=30°,∠EA1B=60°.
8.【答案】;
【解析】设AE=CE=,DE=,,.
9.【答案】8;
【解析】由矩形的性质可知△AOB是等边三角形,∴ AC=2AO=2AB=8.
10.【答案】;
【解析】作FM⊥AD于M,如图所示:
则MF=DC=,由题意可得:CE=,
由折叠可得:PE=CE==2DE,∠EPF=∠C=90°,
∴∠DPE=30°,∴∠MPF=60°,∠MFP=30°,∴FP=.
11.【答案】30或10;
【解析】∵AE平分∠DAB,
∴∠DAE=∠EAB,
∵四边形ABCD是矩形,
∴AD=BC,DC=AB,AD∥BC,
∴∠DEA=∠BEA,
∴∠EAB=∠BEA,
∴AB=BE,
①设BE=x,CE=3x,则AD=4x,AB=x,
∵矩形ABCD的面积为36,
∴x?4x=36,
解得:x=3(舍负),
即AD=BC=4x=12,AB=CD=x=3,
∴矩形的周长为:AB+BC+CD+AD=2×(3+12)=30;
②设BE=3x,CE=x,则AD=4x,AB=3x,
∵矩形ABCD的面积为36,
∴3x?4x=36,
解得:x=(舍负),
即AD=BC=4x=4,AB=CD=x=,
∴矩形的周长为:AB+BC+CD+AD=2×(4+)=10;
故答案为:30或10.
12.【答案】12;
【解析】设BE=EF=,CE=,CF=,DF=,则,解得,矩形ABCD的周长=.
三.解答题
13.【解析】
解:①正确,连接PC,可得PC=EF,PC=PA,∴AP=EF;
②正确;延长AP,交EF于点N,则∠EPN=∠BAP=∠PCE=∠PFE,可得AP⊥EF;
③正确;∠PFE=∠PCE=∠BAP;
④错误,PD=PF=CE;
⑤正确,PB2+PD2=2PA2.
所以正确的有4个:①②③⑤.
14.【解析】
(1)证明:∵BE⊥AC.DF⊥AC,
∴∠BEO=∠DFO=90°,
∵点O是EF的中点,
∴OE=OF,
又∵∠DOF=∠BOE,
∴△BOE≌△DOF(ASA);
(2)解:四边形ABCD是矩形.理由如下:
∵△BOE≌△DOF,
∴OB=OD,
又∵OA=OC,
∴四边形ABCD是平行四边形,
∵OA=BD,OA=AC,
∴BD=AC,
∴ABCD是矩形.
15.【解析】
证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠BAD=90°,AB=CD,
∴∠BEF+∠BFE=90°.
∵EF⊥ED,
∴∠BEF+∠CED=90°.
∴∠BFE=∠CED.
又∵EF=ED,
∴△EBF≌△DCE.
∴BE=CD.
∴BE=AB.∴∠BAE=∠BEA=45°.
∴∠EAD=45°.
∴∠BAE=∠EAD.
∴AE平分∠BAD.
16.
【解答】证明:
(1)∵CE平分∠BCD、CF平分∠GCD,
∴∠BCE=∠DCE,∠DCF=∠GCF,
∵EF∥BC,
∴∠BCE=∠FEC,∠EFC=∠GCF,
∴∠DCE=∠FEC,∠EFC=∠DCF,
∴OE=OC,OF=OC,
∴OE=OF;
(2)∵点O为CD的中点,
∴OD=OC,
又OE=OF,
∴四边形DECF是平行四边形,
∵CE平分∠BCD、CF平分∠GCD,
∴∠DCE==
∴∠DCE+∠DCF==90°,
即∠ECF=90°,
∴四边形DECF是矩形.
【点评】本题主要考查平行线的性质及矩形的判定,证得OE=OF,得出四边形DECF是平行四边形是解题的关键,注意角平分线的应用.
PAGE
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
