浙教版八年级数学下册4.4平行四边形的判定定理提高讲义含答案
文档属性
| 名称 | 浙教版八年级数学下册4.4平行四边形的判定定理提高讲义含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-24 00:00:00 | ||
图片预览




文档简介
平行四边形的判定定理提高讲义
一.选择题
1.(2019秋﹒诸城市期末)已知△ABC(如图1),按图2图3所示的尺规作图痕迹,(不需借助三角形全等)就能推出四边形ABCD是平行四边形的依据是( )
A.两组对边分别平行的四边形是平行四边形
B.对角线互相平分的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.两组对边分别相等的四边形是平行四边形
2.(2019春﹒甘南县期中)以上四个条件中可以判定四边形是平行四边形的有( )
①两组对边分别平行;
②两组对边分别相等;
③有一组对边平行且相等;
④对角线相等.
A.1个 B.2个 C.3个 D.4个
3.(2019春﹒遵义期中)如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )
A.AB=CD B.AB∥CD C.∠A=∠C D.BC=AD
4. (2019春?海南校级月考)如图,在?ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有( )
A.9个 B.8个 C.6个 D.4个
5. 如图,在□ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
A. AE=CF B.DE=BF
C. D.
6.(杭州模拟)如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,
①四边形ACED是平行四边形;
②△BCE是等腰三角形;
③四边形ACEB的周长是10+2;
④四边形ACEB的面积是16.
则以上结论正确的是( )
A.①②③ B.①②④ C.①③④ D.②④
二.填空题
7.已知四边形ABCD的对角线相交于O,给出下列5个条件①AB∥CD?②AD∥BC③AB=CD?④∠BAD=∠DCB,从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有____________组.
8.在?ABCD中,对角线相交于点O,给出下列条件:①AB=CD,AD=BC,②AD=AB,AD∥BC,③AB∥CD,AD∥BC,④AO=CO,BO=DO其中能够判定ABCD是平行四边形的有____________.
9.如图,用9个全等的等边三角形,按图拼成一个几何图案,从该图案中可以找出_____个平行四边形.
10.如图,已知AB=CD,AD=CB,则∠ABC+∠BAD=___________度.
11.(2019春?太原期末)如图,四边形ABCD的对角线AC与BD相交于点O,AD∥BC,若要使四边形是平行四边形,则需要添加的一个条件是 .(只写出一种情况即可)
12.(2019春?成都校级期末)如图,在△ABC中,AB=4,AC=3,BC=5,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为 .
三.解答题
13. 在□ABCD中,对角线BD、AC相交于点O,BE=DF,过点O作线段GH交AD于点G,交BC于点H,顺次连接EH、HF、FG、GE,求证:四边形EHFG是平行四边形.
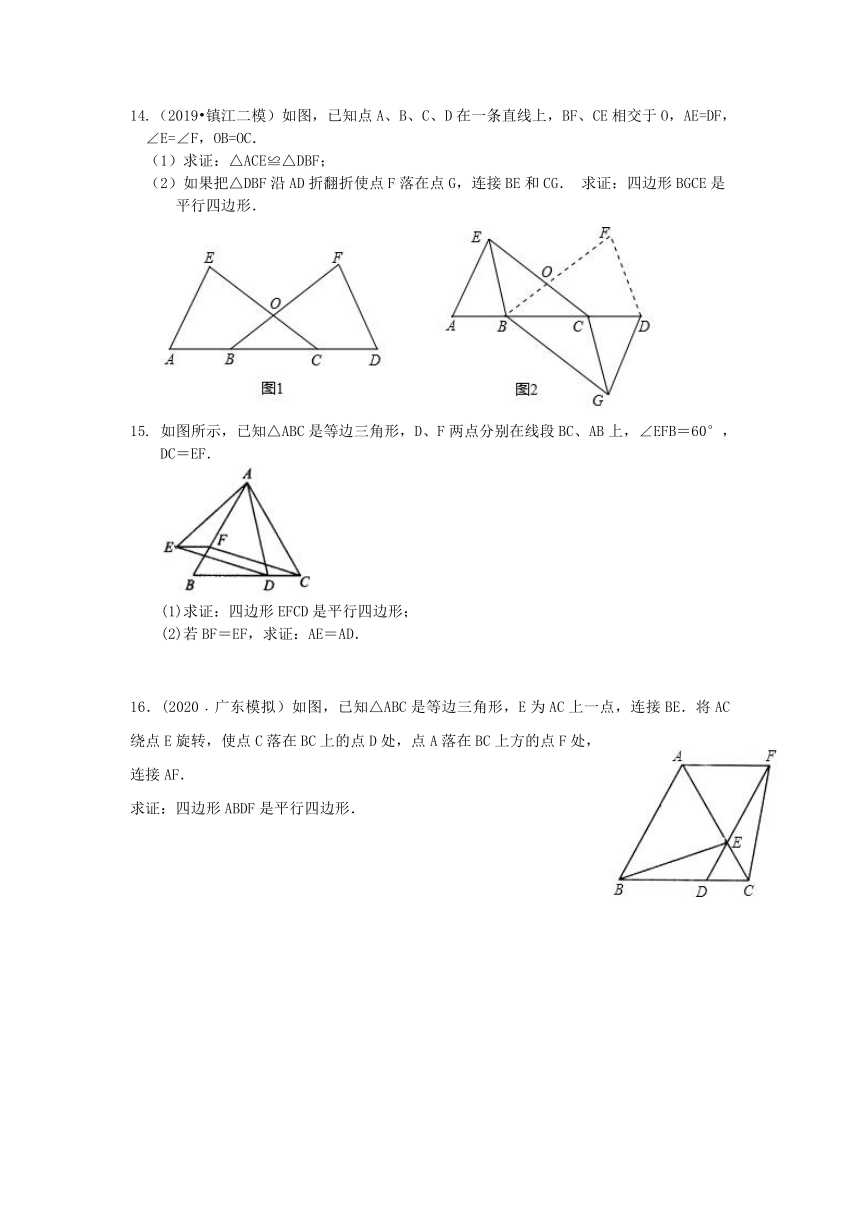
14.(2019?镇江二模)如图,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.
(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,连接BE和CG. 求证:四边形BGCE是平行四边形.
15. 如图所示,已知△ABC是等边三角形,D、F两点分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
16.(2020﹒广东模拟)如图,已知△ABC是等边三角形,E为AC上一点,连接BE.将AC绕点E旋转,使点C落在BC上的点D处,点A落在BC上方的点F处,连接AF.
求证:四边形ABDF是平行四边形.
17.(2020﹒恩施州模拟)如图,在△ABC中,∠BAC=70°,∠ABC和∠ACB的角平分线交于D点,E、F、G、H分别是线段AB、AC、BD、CD的中点.
(1)求∠BDC的度数;
(2)证明:四边形EGHF为平行四边形.
18.(2019春﹒西华县期中)如图,在四边形ABCD中,AD∥BC 且AD=9cm,BC=6cm,点P、Q分别从点A、C同时出发,点P以的速度由A向D运动,点Q以的速度由C向B运动.问几秒后直线PQ将四边形ABCD截出一个平行四边形?
【答案与解析】
一.选择题
1.【答案】B;
2.【答案】C;
3.【答案】A;
4.【答案】B;
【解析】设EF与NH交于点O,∵在?ABCD中,EF∥AD,HN∥AB,
∴AD∥EF∥BC,AB∥NH∥CD,
则图中的四边AEOH、DHOF、BEON、CFON、AEFD、BEFC、AHNB、DHNC
和ABCD都是平行四边形,共9个.
故选B.
5.【答案】B;
【解析】C选项和D选项均可证明△ADE≌△CBF,从而得到AE=CF,EO=FO,BO=DO,所以可证四边形DEBF是平行四边形.
6.【答案】A;
【解析】解:①∵∠ACB=90°,DE⊥BC,
∴∠ACD=∠CDE=90°,
∴AC∥DE,
∵CE∥AD,
∴四边形ACED是平行四边形,故①正确;
②∵D是BC的中点,DE⊥BC,
∴EC=EB,
∴△BCE是等腰三角形,故②正确;
③∵AC=2,∠ADC=30°,
∴AD=4,CD=2,
∵四边形ACED是平行四边形,
∴CE=AD=4,
∵CE=EB,
∴EB=4,DB=2,
∴CB=4,
∴AB==2,
∴四边形ACEB的周长是10+2故③正确;
④四边形ACEB的面积:×2×4+×4×2=8,故④错误,
故选:A.
二.填空题
7.【答案】4;
【解析】①和②根据两组对边分别平行的四边形是平行四边形,能推出四边形ABCD为平行四边形;
①和③根据一组对边平行且相等的四边形是平行四边形,能推出四边形ABCD为平行四边形;
①和④,②和④根据两组对边分别平行的四边形是平行四边形,能推出四边形ABCD为平行四边形;
所以能推出四边形ABCD为平行四边形的有四组.故答案为:4.
8.【答案】①②③④;
【解析】∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,∴①正确;
∵AD=BC,AD∥BC,
∴四边形ABCD是平行四边形,∴②正确;
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,∴③正确;
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,∴④正确;
即其中能判定四边形ABCD是平行四边形的有①②③④,
故答案为:①②③④.
9.【答案】15;
【解析】两个全等的等边三角形,以一边为对角线构成的四边形是平行四边形,这样的两个平行四边形又可组成较大的平行四边形,从该图案中可以找出15个平行四边形.
故答案为:15.
10.【答案】180°;
【解析】依题意得ABCD是平行四边形,
∴AD∥BC,
∴∠ABC+∠BAD=180°.
11.【答案】AD=BC;
【解析】∵AD=BC,AD∥BC,
∴四边形ABCD是平行四边形,
故答案为:AD=BC.
12.【答案】6;
【解析】解:∵在△ABC中,AB=3,AC=4,BC=5,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°.
∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
在△ABC与△DBF中,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证△ABC≌△EFC,
∴AB=EF=AD=3,
∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°﹣∠DAE=30°,
∴S口AEFD=AD?(DF×)=3×(4×)=6.
即四边形AEFD的面积是6.
故答案为:6.
二.解答题
13.【解析】
证明:在ABCD中
AD∥BC,AO=CO,BO=DO
∴∠GAO=∠HCO
在△AGO和△CHO中
∴△AGO≌△CHO
∴GO=HO
又∵BO=DO,BE=DF
∴EO=FO
∴四边形EHFG为平行四边形.
14.【解析】
证明:(1)如图1,
∵OB=OC,
∴∠ACE=∠DBF,
在△ACE和△DBF中,
,
∴△ACE≌△DBF(AAS);
(2)如图2,
∵∠ACE=∠DBF,∠DBG=∠DBF,
∴∠ACE=∠DBG,
∴CE∥BG,
∵CE=BF,BG=BF,
∴CE=BG,
∴四边形BGCE是平行四边形.
15.【解析】
证明:(1)∵ △ABC是等边三角形,
∴ ∠ABC=60°.
又∵ ∠EFB=60°,
∴ EF∥BC,即EF∥DC.
又∵ DC=EF,
∴ 四边形EFCD是平行四边形.
(2)如图,连接BE.
∵ BF=EF,∠EFB=60°,
∴ △EFB是等边三角形,
∴ BE=BF=EF,∠EBF=60°,
∴ DC=EF=BE.
∵ △ABC是等边三角形,
∴ AC=AB,∠ACD=60°.
在△ABE和△ACD中,
∵ AB=AC,∠ABE=∠ACD,BE=CD,
∴ △ABE≌△ACD,
∴ AE=AD.
16.【分析】根据已知条件可以判定△ABC、△DCE均为等边三角形,由等边三角形的三个内角相等、三条边相等,进而得到三个三角形△ABC、△AEF、△DCE是等边三角形,可以推知同位角∠CDE=∠ABC,内错角∠CDE=∠EFA.所以利用平行的线的判定定理可以证得四边形ABDF的对边相互平行.
【解答】证明:∵△ABC是等边三角形,
∴AC=BC=AB,∠ACB=60°;
∵将AC绕点E旋转
∴ED=CE,EF=AE
∴△EDC是等边三角形,
∴DE=CD=CE,∠DCE=∠EDC=60°,
∴FD=AC=BC,
∴△ABC、△AEF、△DCE均为等边三角形,
∴∠CDE=∠ABC=∠EFA=60°,
∴AB∥FD,BD∥AF,
∴四边形ABDF是平行四边形.
17.
【解答】解:(1)∵∠BAC=70°,
∴∠ABC+∠ACB=110°
∵BD、CD分别平分∠ABC和∠ACB,
∴∠DBC==
∴∠DBC+∠DCB==55°
∴∠BDC=180°-(∠DBC+∠DCB)=125°;
(2)证明:∵E、F、G、H分别是AB、AC、BD、CD的中点,
∴EF,GH分别为△ABC和△DBC的中位线
∴EF∥BC,GH∥BC,且EF==
∴EF∥GH,EF=GH
∴四边形EGHF为平行四边形.
18.【解答】解:设点P,Q运动的时间为ts.依题意得:CQ=2t,BQ=6-2t,AP=t,
PD=9-t.
①当BQ=AP时,四边形APQB是平行四边形.
即6-2t=t,
解得t=2.
②当CQ=PD时,
四边形CQPD是平行四边形,即2t=9-t,
解得:t=3.
所以经过2或3秒后,直线PQ将四边形ABCD截出一个平行四边形.
PAGE
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
