浙教版数学八年级下册第四章平行四边形末检测卷含答案
文档属性
| 名称 | 浙教版数学八年级下册第四章平行四边形末检测卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 383.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 12:07:19 | ||
图片预览

文档简介
平行四边形章末检测
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.(2019秋﹒西宁期末)用一批完全相同的正多边形能镶嵌成一个平面图案的是( )
A.正五边形 B.正六边形 C.正七边形 D.正八边形
2.(2019秋﹒岱岳区期末)平行四边形ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得到四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.AE=CF D.∠BAE=∠DCF
3.(2019秋﹒柳州期末)在下列这些汽车标识中,是中心对称图形的是( )
A. B. C. D.
4.(2020﹒郑州模拟)如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=时,EP+BP的值为( )
A.6 B.9 C.12 D.18
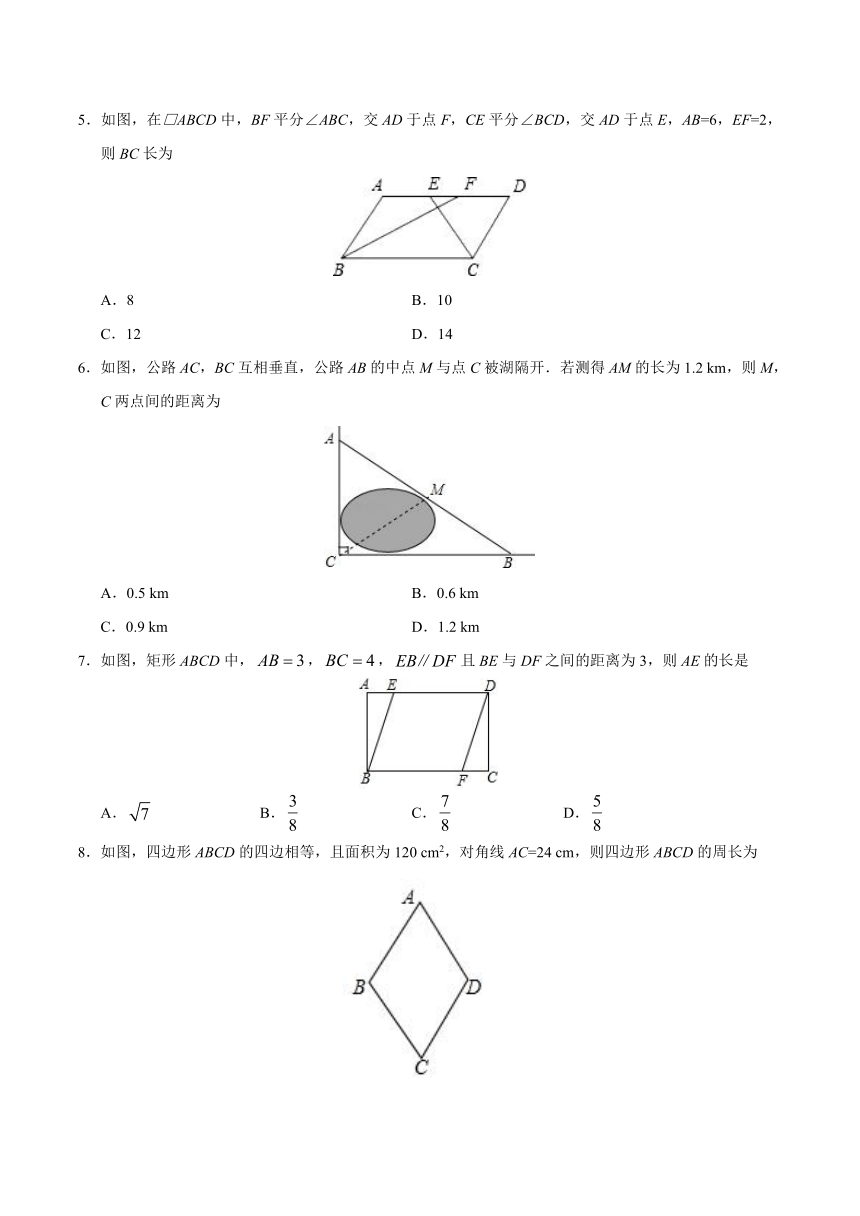
5.如图,在□ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为
A.8 B.10
C.12 D.14
6.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2 km,则M,C两点间的距离为
A.0.5 km B.0.6 km
C.0.9 km D.1.2 km
7.如图,矩形ABCD中,,,且BE与DF之间的距离为3,则AE的长是
A. B. C. D.
8.如图,四边形ABCD的四边相等,且面积为120 cm2,对角线AC=24 cm,则四边形ABCD的周长为
A.52 cm B.40 cm C.39 cm D.26 cm
9.如图,在正方形ABCD中,A、B、C三点的坐标分别是(-1,2)、(-1,0)、(-3,0),将正方形ABCD向右平移3个单位,则平移后点D的坐标是
A.(-6,2) B.(0,2) C.(2,0) D.(2,2)
10.如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为
A. B. C. D.
二、填空题(本大题共10小题,每小题3分,共30分)
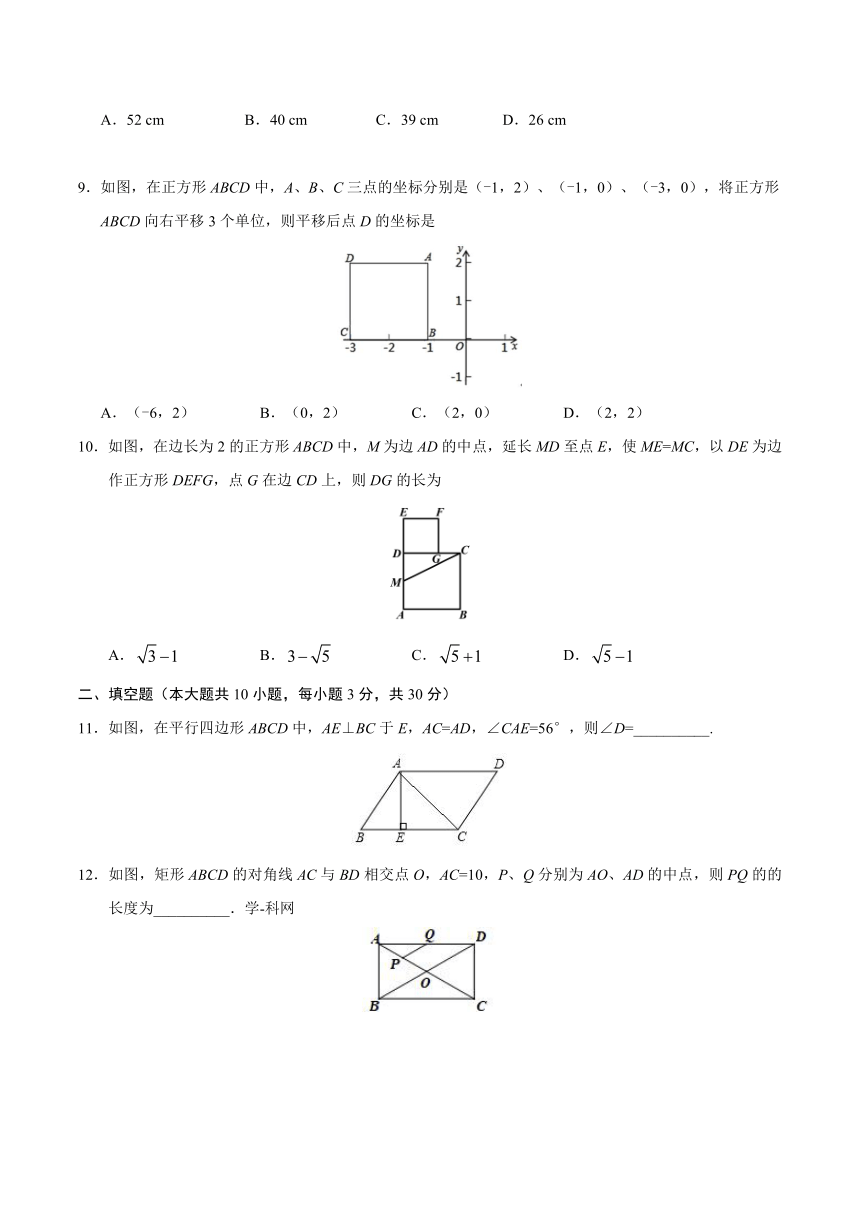
11.如图,在平行四边形ABCD中,AE⊥BC于E,AC=AD,∠CAE=56°,则∠D=__________.
12.如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P、Q分别为AO、AD的中点,则PQ的的长度为__________.学-科网
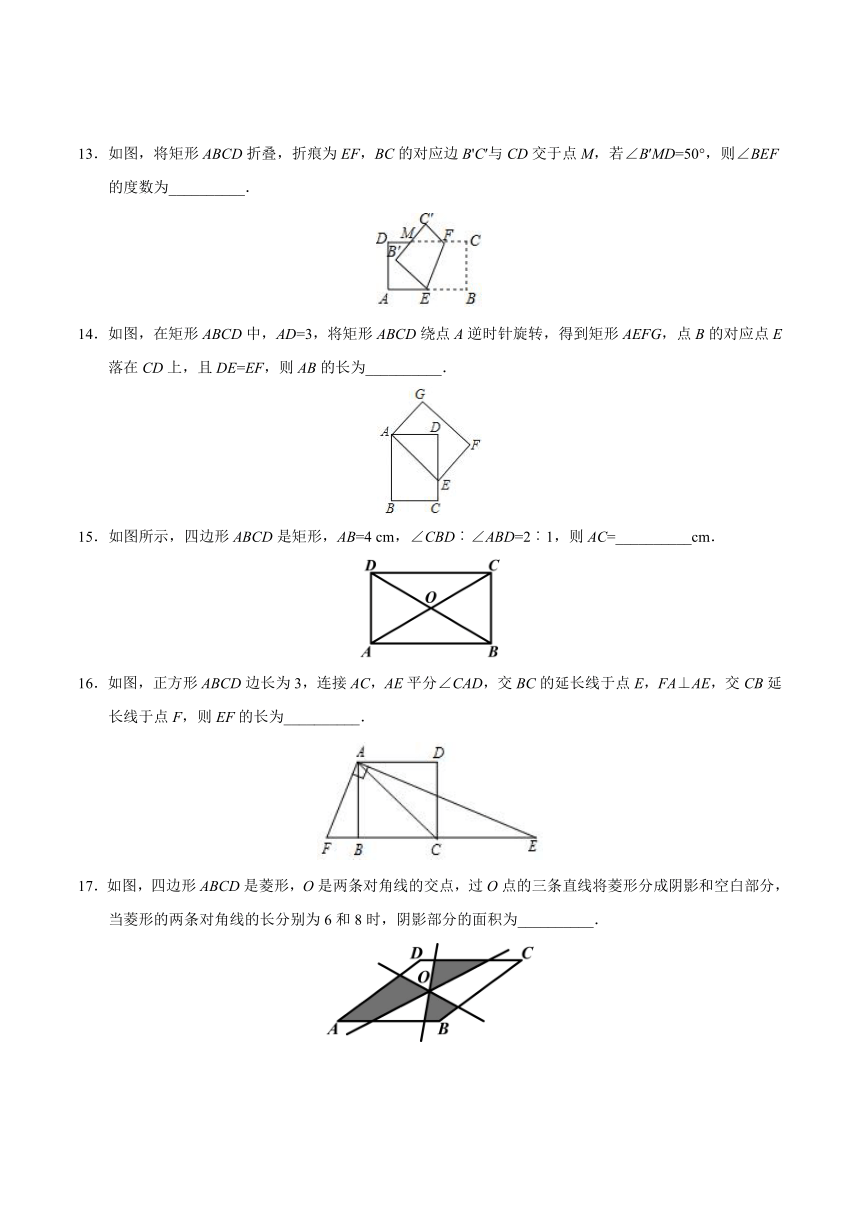
13.如图,将矩形ABCD折叠,折痕为EF,BC的对应边B'C′与CD交于点M,若∠B′MD=50°,则∠BEF的度数为__________.
14.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为__________.
15.如图所示,四边形ABCD是矩形,AB=4 cm,∠CBD︰∠ABD=2︰1,则AC=__________cm.
16.如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.
17.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为6和8时,阴影部分的面积为__________.
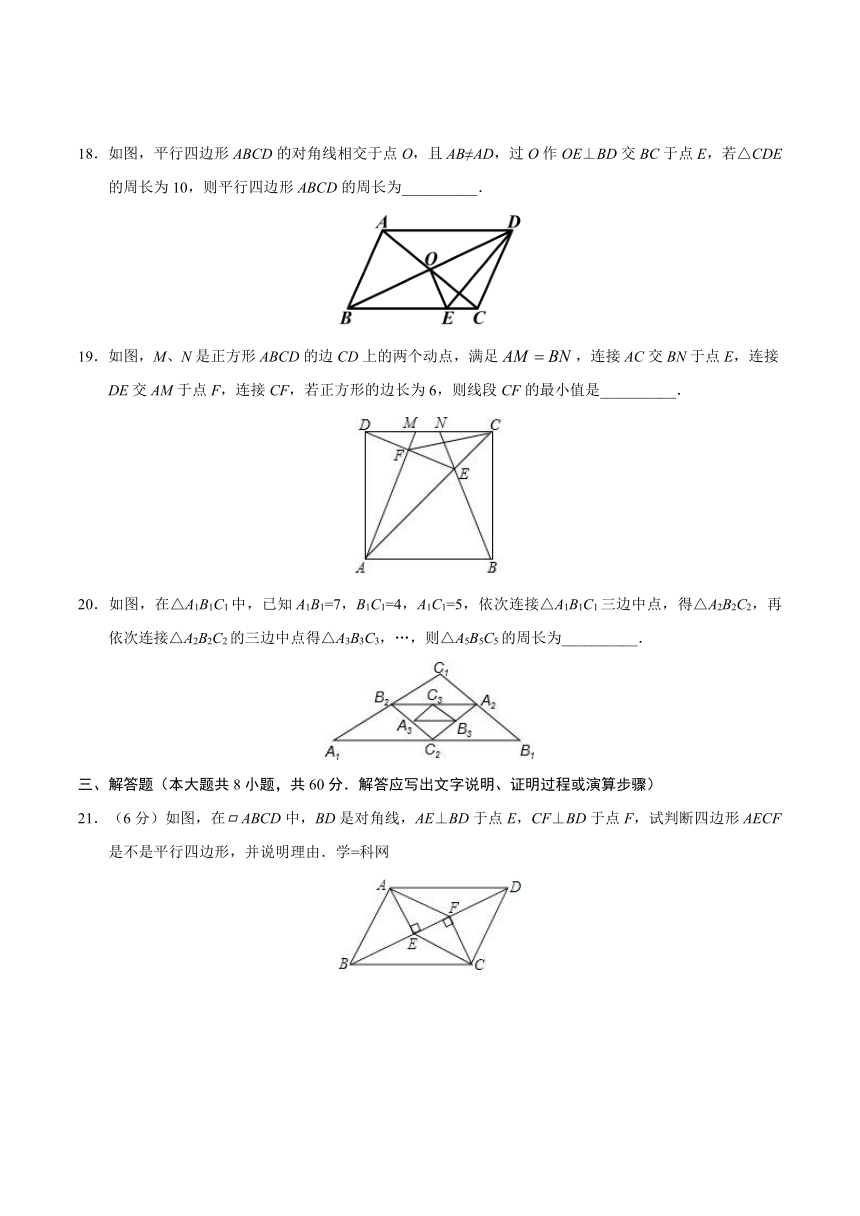
18.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E,若△CDE的周长为10,则平行四边形ABCD的周长为__________.
19.如图,M、N是正方形ABCD的边CD上的两个动点,满足,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为6,则线段CF的最小值是__________.
20.如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=5,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点得△A3B3C3,…,则△A5B5C5的周长为__________.
三、解答题(本大题共8小题,共60分.解答应写出文字说明、证明过程或演算步骤)
21.(6分)如图,在ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断四边形AECF是不是平行四边形,并说明理由.学=科网
22.(6分)如图,在ABCD中,AB=DB,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DFBE是矩形.
23.(6分)如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
24.(8分)已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
25.(8分)如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
26.(8分)如图,对折矩形纸片ABCD,使AB与DC重合,得到折痕MN,将纸片展平;再一次折叠,使点D落到MN上的点F处,折痕AP交MN于E;延长PF交AB于G.求证:
(1)△AFG≌△AFP;
(2)△APG为等边三角形.
27.(2019春﹒玄武区校级期中)定义:若△ABC中,其中一个内角是另一个内角的一半,则称△ABC为“半角三角形”.根据此定义,完成下面各题:
(1)若△ABC为半角三角形,且∠A=90°,则△ABC中其余两个角的度数为 ;
(2)若△ABC是半角三角形,且∠C=40°,则∠B= ;
(3)如图,在四边形ABCD中,AB∥CD,AD∥BC,∠C=72°,点E在边CD上,以BE为折痕,将△BCE向上翻折,点C恰好落在AD边上的点F,若BF⊥AD,则△EDF是半角三角形吗?若是,请说明理由.
28.(2019春﹒滕州市期末)如图,在□ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为当t=4时,求y的值.
参考答案
1.【答案】B
2.【答案】C
3.【答案】B
4. 【答案】C
5.【答案】B
【解析】根据平行四边形的性质可知AB=CD,AD∥BC,AD=BC,然后根据平行线的性质和角平分线的
性质可知AB=AF,DE=CD,因此可知AF+DE=AD+EF=2AB=12,解得AD=BC=12-2=10.故选B.
6.【答案】D
【解析】根据直角三角形斜边上的中线等于斜边的一半即可求得距离为1.2 km.故选D.
7.【答案】C
【解析】如图,过点D作,垂足为G,则,
∵,,,∴≌,∴,
设,则,在中,,,解得,故选C.
8.【答案】A.
【解析】如图,连接AC、BD相交于点O,∵四边形ABCD的四边相等,∴四边形ABCD为菱形,∴AC⊥BD,S四边形ABCD=AC·BD,∴×24BD=120,解得BD=10 cm,∴OA=12 cm,OB=5 cm,在Rt△AOB中,由勾股定理可得AB==13(cm),∴四边形ABCD的周长=4×13=52(cm),故选A.
9.【答案】B
【解析】∵在正方形ABCD中,A、B、C三点的坐标分别是(-1,2),(-1,0),(-3,0),
∴D(-3,2),∴将正方形ABCD向右平移3个单位,则平移后点D的坐标是(0,2),故选B.
10.【答案】D
【解析】∵四边形ABCD为正方形,∴DC=DA=2.∵M为边AD的中点,∴DM=1,
∴,∴.故选D.
11.【答案】73°
【解析】∵ ,∴,∵,∴,在平行四边形ABCD中,∴,∵,∠.故答案为:73°.
12.【答案】2.5
【解析】∵四边形ABCD是矩形,∴AC=BD=10,BO=DO=BD,∴OD=BD=5,∵点P、Q是AO,AD的中点,∴PQ是△AOD的中位线,∴PQ=DO=2.5.故答案为:2.5.
13.【答案】70°
【解析】∵∠C'=∠C=90°,∠DMB'=∠C'MF=50°,∴∠C'FM=40°,设∠BEF=α,则∠EFC=180°-α,
∠DFE=∠BEF=α,∠C'FE=40°+α,由折叠可得,∠EFC=∠EFC',∴180°-α=40°+α,∴α=70°,
∴∠BEF=70°,故答案为:70°.
14.【答案】3
【解析】∵四边形ABCD是矩形,∴∠D=90°,BC=AD=3,∵将矩形ABCD绕点A逆时针旋转得到矩形AEFG,∴EF=BC=3,AE=AB,∵DE=EF,∴AD=DE=3,∴AE==3,∴AB=3,故答案为:3.
15.【答案】
【解析】设∠CBD=2x,∠ABD=x,则2x+x=90°,所以x=30°.又因为OA=OB,所以∠OAB=30°.
在Rt△ABC中,设BC=y cm,则AC=2y cm,所以(2y)2–y2=42,解得.∴cm.
故答案为:.
16.【答案】6
【解析】∵四边形ABCD为正方形,且边长为3,∴AC=3,∵AE平分∠CAD,∴∠CAE=∠DAE,
∵AD∥CE,∴∠DAE=∠E,∴∠CAE=∠E,∴CE=cA=3,∵FA⊥AE,∴∠FAC+∠CAE=90°
∠F+∠E=90°,∴∠FAC=∠F,∴CF=AC=3,∴EF=CF+CE=3+3=6.故答案为:6
17.【答案】12
【解析】∵菱形的两条对角线的长分别为6和8,∴菱形的面积.∵O是菱形两条对角线的交点,∴阴影部分的面积.故答案为:12.
18.【答案】20
【解析】∵四边形ABCD是平行四边形,∴O是BD的中点,又∵OE⊥BD,∴DE=BE.∵△CDE的周长为10,∴CD+DE+CE=10,∴CD+CE+BE=CD+BC=10,∴ABCD的周长=2(CD+BC)=2×10=20.故答案为:20.
19.【答案】
【解析】如图,
在正方形ABCD中,,,,
在和中,,∴≌,∴,
在和中,,∴≌,∴,
∴,∵,∴,
∴,取AD的中点O,连接OF、OC,则,
在中,,根据三角形的三边关系,,
∴当O、F、C三点共线时,CF的长度最小,最小值,故答案为:.
20.【答案】1
【解析】根据三角形的中位线定理得:A2B2、B2C2、C2A2分别等于A1B1、B1C1、C1A1的一半,所以△A2B2C2的周长等于△A1B1C1的周长的一半,以此类推可求△A5B5C5的周长为△A1B1C1的周长的,则周长=(7+4+5)×=1.故答案为:1.
21.【解析】四边形AECF是平行四边形,理由如下:
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEF=∠CFE=90°,
∴AE∥CF(内错角相等,两直线平行),
在平行四边形ABCD中,AB=CD,AB∥CD,
∴∠ABE=∠CDF,
在△ABE与△DCF中,,
∴△ABE≌△CDF(AAS),
∴AE=CF,
∴四边形AECF是平行四边形(有一组对边平行且相等的四边形是平行四边形).
22.【解析】∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥AB,
∴∠CDB=∠ABD.
∵BE平分∠ABD,DF平分∠CDB,
∴,,
∴∠FDB=∠EBD,∴DF∥BE.
∵AD∥BC,DF∥BE,
∴四边形DFBE是平行四边形.
∵AB=DB,BE平分∠ABD,
∴∠DEB=90°,
∴四边形DFBE是矩形.
23.【解析】(1)∵四边形ABCD是平行四边形,
∴CD∥AB,
∵BM⊥AC,DN⊥AC,
∴DN∥BM,
∴四边形BMDN是平行四边形.
(2)∵四边形BMDN是平行四边形,
∴DM=BN,
∵CD=AB,CD∥AB,
∴CM=AN,∠MCE=∠NAF,
∵∠CEM=∠AFN=90°
∴△CEM≌△AFN,
∴FN=EM=5,
在Rt△AFN中,AN=
24.【解析】(1)如图,连接EF,
∵点F,G,H分别是BC,BE,CE的中点,
∴FH∥BE,FH=BE,FH=BG,
∴∠CFH=∠CBG,
∵BF=CF,
∴△BGF≌△FHC.
(2)当四边形EGFH是正方形时,连接GH,可得:EF⊥GH且EF=GH,
∵在△BEC中,点G,H分别是BE,CE的中点,
∴且GH∥BC,
∴EF⊥BC,
∵AD∥BC,AB⊥BC,
∴AB=EF=GH=a,
∴矩形ABCD的面积=.
25.【解析】(1)∵AB=AC,AH⊥CB,∴BH=HC.
∵FH=EH,∴四边形EBFC是平行四边形.
又∵AH⊥CB,∴四边形EBFC是菱形.
(2)如图,
∵四边形EBFC是菱形.∴∠2=∠3=∠ECF.
∵AB=AC,AH⊥CB,∴∠4=∠BAC.
∵∠BAC=∠ECF,
∴∠4=∠3.
∵AH⊥CB,
∴∠4+∠1+∠2=90°,
∴∠3+∠1+∠2=90°,
即:AC⊥CF.
26.【解析】(1)由折叠可得:M、N分别为AD、BC的中点,
∵DC∥MN∥AB,
∴F为PG的中点,即PF=GF,
由折叠可得:∠PFA=∠D=90°,∠1=∠2,
在△AFP和△AFG中,,
∴△AFP≌△AFG(SAS).
(2)∵△AFP≌△AFG,
∴AP=AG,
∵AF⊥PG,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠2=∠3=30°,
∴∠2+∠3=60°,即∠PAG=60°,
∴△APG为等边三角形.
27.【分析】(1)分两种情况进行解答,①若另一个锐角等于∠A=90°的一半,②若除∠A以外的两个角中,有一个角是另一个的一半,根据三角形的内角和为180°,进行解答,
(2)分六种情况进行讨论解答,把其中的一个内角等于另一个内角的一半的情况都进行考虑,分别求出相应的角的度数.
(3)根据题意分别求出三角形DEF的各个内角的度数,结合“半角三角形”的意义进行判断.
【解答】解:(1)①若另一个锐角等于∠A=90°的一半,则这个角为45°,第三角为45°,
②若除∠A以外的两个角中,有一个角是另一个的一半,则有较小的角为(180°-90°)÷(1+2)=30°.
那么较大的角为60°,
故答案为:45°,45°或30°,60°,
(2)根据题意有以下几种情况:
①若∠B=则∠B=20°,
②若∠C=则∠B=80°,
③若∠A=则∠A=20°,∠B=120°,
④若∠C=则∠A=80°,∠B=60°,
⑤若∠B=则∠B=(180°-40°)÷3=
⑥若∠A=则∠B=(180°-40°)÷3×2=
(3)∵AB∥CD,AD∥BC,∠C=72°,
∴ABCD是平行四边形,
∴∠C=∠A=72°,∠D=∠ABC=180°-72°=108°,
由折叠得,∠C=∠BFE=72°,
∵BF⊥AD,
∴∠AFB=90°,
∴∠DFE=180°-90°-72°=18°,
∴∠DEF=180°-108°-18°=54°
∴∠DEF=
∴△EDF是半角三角形.
28.解:(1)当t=2.5s时,四边形ABQP是平行四边形,
理由是:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=3cm,AD=BC=5cm,AO=CO,BO=OD,
∴∠PAO=∠QCO,
∴△APO≌△CQO(ASA),
∴AP=CQ=2.5cm,
∵BC=5cm,
∴BQ=5cm-2.5cm=2.5cm=AP,
即AP=BQ,AP∥BQ,
∴四边形ABQP是平行四边形,
即当t=2.5s时,四边形ABQP是平行四边形;
(2)过A作AM⊥BC于M,过O作ON⊥BC于N,
∵AB⊥AC,AB=3cm,BC=5cm,
∴在Rt△ABC中,由勾股定理得:AC=4cm,
∵由三角形的面积公式得:==
∴3×4=5×AM,
∴AM=2.4(cm),
∵ON⊥BC,AM⊥BC,
∴AM∥ON,
∵AO=OC,
∴MN=CN,
∴ON==1.2cm,
∵在△BAC和△DCA中
∴△BAC≌△DCA(SSS),
∴===
∵AO=OC,
∴△DOC的面积==
当t=4s时,AP=CQ=4cm,
∴△OQC的面积为=
∴y==.
【点评】本题考查了平行四边形的性质和判定,三角形的面积,全等三角形的性质和判定等知识点,能综合运用定理进行推理是解此题的关键.
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.(2019秋﹒西宁期末)用一批完全相同的正多边形能镶嵌成一个平面图案的是( )
A.正五边形 B.正六边形 C.正七边形 D.正八边形
2.(2019秋﹒岱岳区期末)平行四边形ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得到四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.AE=CF D.∠BAE=∠DCF
3.(2019秋﹒柳州期末)在下列这些汽车标识中,是中心对称图形的是( )
A. B. C. D.
4.(2020﹒郑州模拟)如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=时,EP+BP的值为( )
A.6 B.9 C.12 D.18
5.如图,在□ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为
A.8 B.10
C.12 D.14
6.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2 km,则M,C两点间的距离为
A.0.5 km B.0.6 km
C.0.9 km D.1.2 km
7.如图,矩形ABCD中,,,且BE与DF之间的距离为3,则AE的长是
A. B. C. D.
8.如图,四边形ABCD的四边相等,且面积为120 cm2,对角线AC=24 cm,则四边形ABCD的周长为
A.52 cm B.40 cm C.39 cm D.26 cm
9.如图,在正方形ABCD中,A、B、C三点的坐标分别是(-1,2)、(-1,0)、(-3,0),将正方形ABCD向右平移3个单位,则平移后点D的坐标是
A.(-6,2) B.(0,2) C.(2,0) D.(2,2)
10.如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为
A. B. C. D.
二、填空题(本大题共10小题,每小题3分,共30分)
11.如图,在平行四边形ABCD中,AE⊥BC于E,AC=AD,∠CAE=56°,则∠D=__________.
12.如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P、Q分别为AO、AD的中点,则PQ的的长度为__________.学-科网
13.如图,将矩形ABCD折叠,折痕为EF,BC的对应边B'C′与CD交于点M,若∠B′MD=50°,则∠BEF的度数为__________.
14.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为__________.
15.如图所示,四边形ABCD是矩形,AB=4 cm,∠CBD︰∠ABD=2︰1,则AC=__________cm.
16.如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.
17.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为6和8时,阴影部分的面积为__________.
18.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E,若△CDE的周长为10,则平行四边形ABCD的周长为__________.
19.如图,M、N是正方形ABCD的边CD上的两个动点,满足,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为6,则线段CF的最小值是__________.
20.如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=5,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点得△A3B3C3,…,则△A5B5C5的周长为__________.
三、解答题(本大题共8小题,共60分.解答应写出文字说明、证明过程或演算步骤)
21.(6分)如图,在ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断四边形AECF是不是平行四边形,并说明理由.学=科网
22.(6分)如图,在ABCD中,AB=DB,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DFBE是矩形.
23.(6分)如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
24.(8分)已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
25.(8分)如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
26.(8分)如图,对折矩形纸片ABCD,使AB与DC重合,得到折痕MN,将纸片展平;再一次折叠,使点D落到MN上的点F处,折痕AP交MN于E;延长PF交AB于G.求证:
(1)△AFG≌△AFP;
(2)△APG为等边三角形.
27.(2019春﹒玄武区校级期中)定义:若△ABC中,其中一个内角是另一个内角的一半,则称△ABC为“半角三角形”.根据此定义,完成下面各题:
(1)若△ABC为半角三角形,且∠A=90°,则△ABC中其余两个角的度数为 ;
(2)若△ABC是半角三角形,且∠C=40°,则∠B= ;
(3)如图,在四边形ABCD中,AB∥CD,AD∥BC,∠C=72°,点E在边CD上,以BE为折痕,将△BCE向上翻折,点C恰好落在AD边上的点F,若BF⊥AD,则△EDF是半角三角形吗?若是,请说明理由.
28.(2019春﹒滕州市期末)如图,在□ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0
(2)设四边形OQCD的面积为当t=4时,求y的值.
参考答案
1.【答案】B
2.【答案】C
3.【答案】B
4. 【答案】C
5.【答案】B
【解析】根据平行四边形的性质可知AB=CD,AD∥BC,AD=BC,然后根据平行线的性质和角平分线的
性质可知AB=AF,DE=CD,因此可知AF+DE=AD+EF=2AB=12,解得AD=BC=12-2=10.故选B.
6.【答案】D
【解析】根据直角三角形斜边上的中线等于斜边的一半即可求得距离为1.2 km.故选D.
7.【答案】C
【解析】如图,过点D作,垂足为G,则,
∵,,,∴≌,∴,
设,则,在中,,,解得,故选C.
8.【答案】A.
【解析】如图,连接AC、BD相交于点O,∵四边形ABCD的四边相等,∴四边形ABCD为菱形,∴AC⊥BD,S四边形ABCD=AC·BD,∴×24BD=120,解得BD=10 cm,∴OA=12 cm,OB=5 cm,在Rt△AOB中,由勾股定理可得AB==13(cm),∴四边形ABCD的周长=4×13=52(cm),故选A.
9.【答案】B
【解析】∵在正方形ABCD中,A、B、C三点的坐标分别是(-1,2),(-1,0),(-3,0),
∴D(-3,2),∴将正方形ABCD向右平移3个单位,则平移后点D的坐标是(0,2),故选B.
10.【答案】D
【解析】∵四边形ABCD为正方形,∴DC=DA=2.∵M为边AD的中点,∴DM=1,
∴,∴.故选D.
11.【答案】73°
【解析】∵ ,∴,∵,∴,在平行四边形ABCD中,∴,∵,∠.故答案为:73°.
12.【答案】2.5
【解析】∵四边形ABCD是矩形,∴AC=BD=10,BO=DO=BD,∴OD=BD=5,∵点P、Q是AO,AD的中点,∴PQ是△AOD的中位线,∴PQ=DO=2.5.故答案为:2.5.
13.【答案】70°
【解析】∵∠C'=∠C=90°,∠DMB'=∠C'MF=50°,∴∠C'FM=40°,设∠BEF=α,则∠EFC=180°-α,
∠DFE=∠BEF=α,∠C'FE=40°+α,由折叠可得,∠EFC=∠EFC',∴180°-α=40°+α,∴α=70°,
∴∠BEF=70°,故答案为:70°.
14.【答案】3
【解析】∵四边形ABCD是矩形,∴∠D=90°,BC=AD=3,∵将矩形ABCD绕点A逆时针旋转得到矩形AEFG,∴EF=BC=3,AE=AB,∵DE=EF,∴AD=DE=3,∴AE==3,∴AB=3,故答案为:3.
15.【答案】
【解析】设∠CBD=2x,∠ABD=x,则2x+x=90°,所以x=30°.又因为OA=OB,所以∠OAB=30°.
在Rt△ABC中,设BC=y cm,则AC=2y cm,所以(2y)2–y2=42,解得.∴cm.
故答案为:.
16.【答案】6
【解析】∵四边形ABCD为正方形,且边长为3,∴AC=3,∵AE平分∠CAD,∴∠CAE=∠DAE,
∵AD∥CE,∴∠DAE=∠E,∴∠CAE=∠E,∴CE=cA=3,∵FA⊥AE,∴∠FAC+∠CAE=90°
∠F+∠E=90°,∴∠FAC=∠F,∴CF=AC=3,∴EF=CF+CE=3+3=6.故答案为:6
17.【答案】12
【解析】∵菱形的两条对角线的长分别为6和8,∴菱形的面积.∵O是菱形两条对角线的交点,∴阴影部分的面积.故答案为:12.
18.【答案】20
【解析】∵四边形ABCD是平行四边形,∴O是BD的中点,又∵OE⊥BD,∴DE=BE.∵△CDE的周长为10,∴CD+DE+CE=10,∴CD+CE+BE=CD+BC=10,∴ABCD的周长=2(CD+BC)=2×10=20.故答案为:20.
19.【答案】
【解析】如图,
在正方形ABCD中,,,,
在和中,,∴≌,∴,
在和中,,∴≌,∴,
∴,∵,∴,
∴,取AD的中点O,连接OF、OC,则,
在中,,根据三角形的三边关系,,
∴当O、F、C三点共线时,CF的长度最小,最小值,故答案为:.
20.【答案】1
【解析】根据三角形的中位线定理得:A2B2、B2C2、C2A2分别等于A1B1、B1C1、C1A1的一半,所以△A2B2C2的周长等于△A1B1C1的周长的一半,以此类推可求△A5B5C5的周长为△A1B1C1的周长的,则周长=(7+4+5)×=1.故答案为:1.
21.【解析】四边形AECF是平行四边形,理由如下:
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEF=∠CFE=90°,
∴AE∥CF(内错角相等,两直线平行),
在平行四边形ABCD中,AB=CD,AB∥CD,
∴∠ABE=∠CDF,
在△ABE与△DCF中,,
∴△ABE≌△CDF(AAS),
∴AE=CF,
∴四边形AECF是平行四边形(有一组对边平行且相等的四边形是平行四边形).
22.【解析】∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥AB,
∴∠CDB=∠ABD.
∵BE平分∠ABD,DF平分∠CDB,
∴,,
∴∠FDB=∠EBD,∴DF∥BE.
∵AD∥BC,DF∥BE,
∴四边形DFBE是平行四边形.
∵AB=DB,BE平分∠ABD,
∴∠DEB=90°,
∴四边形DFBE是矩形.
23.【解析】(1)∵四边形ABCD是平行四边形,
∴CD∥AB,
∵BM⊥AC,DN⊥AC,
∴DN∥BM,
∴四边形BMDN是平行四边形.
(2)∵四边形BMDN是平行四边形,
∴DM=BN,
∵CD=AB,CD∥AB,
∴CM=AN,∠MCE=∠NAF,
∵∠CEM=∠AFN=90°
∴△CEM≌△AFN,
∴FN=EM=5,
在Rt△AFN中,AN=
24.【解析】(1)如图,连接EF,
∵点F,G,H分别是BC,BE,CE的中点,
∴FH∥BE,FH=BE,FH=BG,
∴∠CFH=∠CBG,
∵BF=CF,
∴△BGF≌△FHC.
(2)当四边形EGFH是正方形时,连接GH,可得:EF⊥GH且EF=GH,
∵在△BEC中,点G,H分别是BE,CE的中点,
∴且GH∥BC,
∴EF⊥BC,
∵AD∥BC,AB⊥BC,
∴AB=EF=GH=a,
∴矩形ABCD的面积=.
25.【解析】(1)∵AB=AC,AH⊥CB,∴BH=HC.
∵FH=EH,∴四边形EBFC是平行四边形.
又∵AH⊥CB,∴四边形EBFC是菱形.
(2)如图,
∵四边形EBFC是菱形.∴∠2=∠3=∠ECF.
∵AB=AC,AH⊥CB,∴∠4=∠BAC.
∵∠BAC=∠ECF,
∴∠4=∠3.
∵AH⊥CB,
∴∠4+∠1+∠2=90°,
∴∠3+∠1+∠2=90°,
即:AC⊥CF.
26.【解析】(1)由折叠可得:M、N分别为AD、BC的中点,
∵DC∥MN∥AB,
∴F为PG的中点,即PF=GF,
由折叠可得:∠PFA=∠D=90°,∠1=∠2,
在△AFP和△AFG中,,
∴△AFP≌△AFG(SAS).
(2)∵△AFP≌△AFG,
∴AP=AG,
∵AF⊥PG,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠2=∠3=30°,
∴∠2+∠3=60°,即∠PAG=60°,
∴△APG为等边三角形.
27.【分析】(1)分两种情况进行解答,①若另一个锐角等于∠A=90°的一半,②若除∠A以外的两个角中,有一个角是另一个的一半,根据三角形的内角和为180°,进行解答,
(2)分六种情况进行讨论解答,把其中的一个内角等于另一个内角的一半的情况都进行考虑,分别求出相应的角的度数.
(3)根据题意分别求出三角形DEF的各个内角的度数,结合“半角三角形”的意义进行判断.
【解答】解:(1)①若另一个锐角等于∠A=90°的一半,则这个角为45°,第三角为45°,
②若除∠A以外的两个角中,有一个角是另一个的一半,则有较小的角为(180°-90°)÷(1+2)=30°.
那么较大的角为60°,
故答案为:45°,45°或30°,60°,
(2)根据题意有以下几种情况:
①若∠B=则∠B=20°,
②若∠C=则∠B=80°,
③若∠A=则∠A=20°,∠B=120°,
④若∠C=则∠A=80°,∠B=60°,
⑤若∠B=则∠B=(180°-40°)÷3=
⑥若∠A=则∠B=(180°-40°)÷3×2=
(3)∵AB∥CD,AD∥BC,∠C=72°,
∴ABCD是平行四边形,
∴∠C=∠A=72°,∠D=∠ABC=180°-72°=108°,
由折叠得,∠C=∠BFE=72°,
∵BF⊥AD,
∴∠AFB=90°,
∴∠DFE=180°-90°-72°=18°,
∴∠DEF=180°-108°-18°=54°
∴∠DEF=
∴△EDF是半角三角形.
28.解:(1)当t=2.5s时,四边形ABQP是平行四边形,
理由是:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=3cm,AD=BC=5cm,AO=CO,BO=OD,
∴∠PAO=∠QCO,
∴△APO≌△CQO(ASA),
∴AP=CQ=2.5cm,
∵BC=5cm,
∴BQ=5cm-2.5cm=2.5cm=AP,
即AP=BQ,AP∥BQ,
∴四边形ABQP是平行四边形,
即当t=2.5s时,四边形ABQP是平行四边形;
(2)过A作AM⊥BC于M,过O作ON⊥BC于N,
∵AB⊥AC,AB=3cm,BC=5cm,
∴在Rt△ABC中,由勾股定理得:AC=4cm,
∵由三角形的面积公式得:==
∴3×4=5×AM,
∴AM=2.4(cm),
∵ON⊥BC,AM⊥BC,
∴AM∥ON,
∵AO=OC,
∴MN=CN,
∴ON==1.2cm,
∵在△BAC和△DCA中
∴△BAC≌△DCA(SSS),
∴===
∵AO=OC,
∴△DOC的面积==
当t=4s时,AP=CQ=4cm,
∴△OQC的面积为=
∴y==.
【点评】本题考查了平行四边形的性质和判定,三角形的面积,全等三角形的性质和判定等知识点,能综合运用定理进行推理是解此题的关键.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
