浙教版八年级数学下册 4.2平行四边形巩固练习(基础)(部分含解析)
文档属性
| 名称 | 浙教版八年级数学下册 4.2平行四边形巩固练习(基础)(部分含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 18:58:48 | ||
图片预览


文档简介
《平行四边形及其性质》巩固练习(基础)
一.选择题
1. (2020﹒河北模拟)如图,ABCD是平行四边形,则下列各角中最大的是( )
A.∠1 B.∠2 C.∠3 D.∠4
2. (2020﹒武汉模拟)如图,已知平行四边形ABCD的两条对角线交于平面直角坐标系的原点,点A的坐标为(-3,4),则点C的坐标为( )
A.(-3,-4) B.(-3,4) C.(-4,3) D.(3,-4)
3. (2019秋﹒垦利区期末)如图,将一张平行四边形纸片撕开并向两边水平拉伸,若拉开的距离为1cm,AB=2cm,∠B=60°,则拉开部分的面积(即阴影面积)是( )
A. B. C. D.
4.(金华校级月考)如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )
A.AB∥PC B.△ABC的面积等于△BCP的面积
C.AC=BP D.△ABC的周长等于△BCP的周长
5. 平行四边形的一边长是10,那么它的两条对角线的长可以是( )
A.4和6 B.6和8 C.8和10 D.10和12
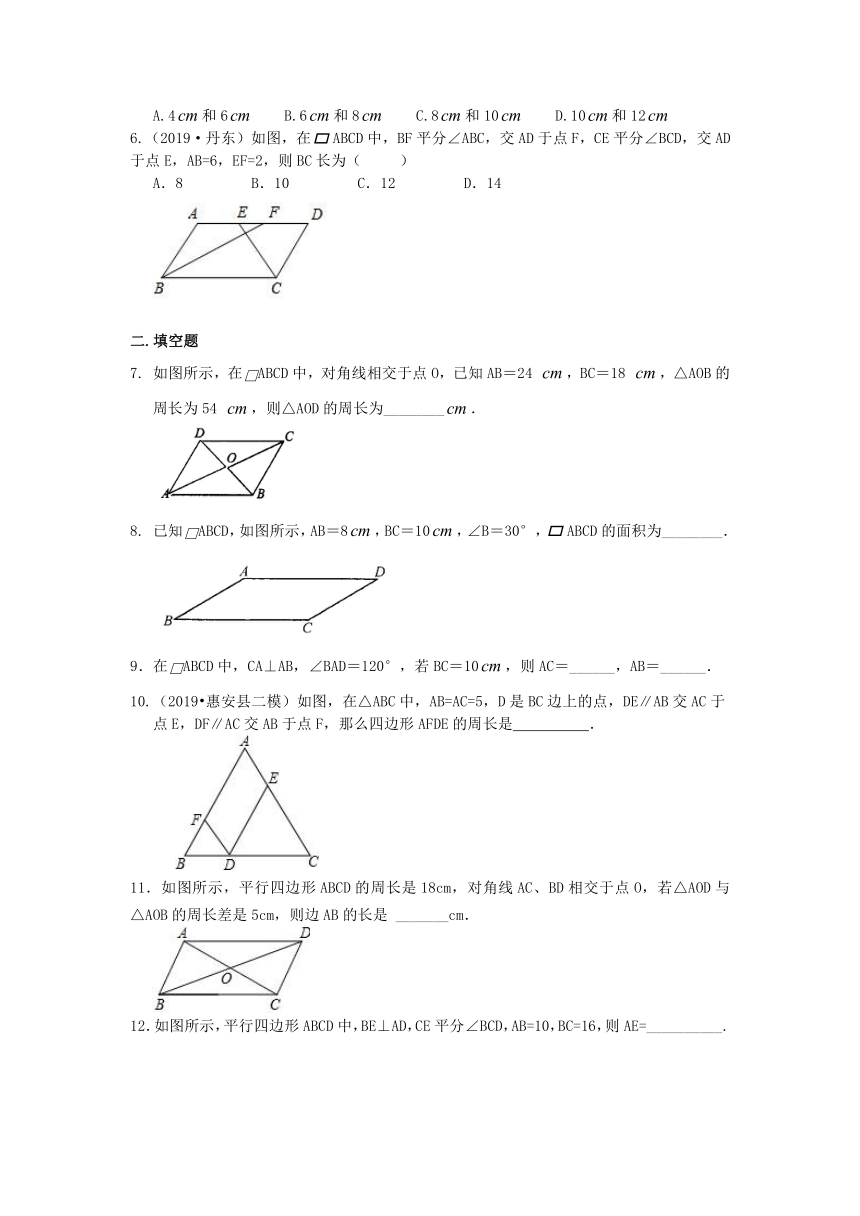
6.(2019·丹东)如图,在ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A.8 B.10 C.12 D.14
二.填空题
7. 如图所示,在□ABCD中,对角线相交于点O,已知AB=24 ,BC=18 ,△AOB的周长为54 ,则△AOD的周长为________.
8. 已知□ABCD,如图所示,AB=8,BC=10,∠B=30°,ABCD的面积为________.
9.在□ABCD中,CA⊥AB,∠BAD=120°,若BC=10,则AC=______,AB=______.
10.(2019?惠安县二模)如图,在△ABC中,AB=AC=5,D是BC边上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是 .
11.如图所示,平行四边形ABCD的周长是18cm,对角线AC、BD相交于点O,若△AOD与△AOB的周长差是5cm,则边AB的长是 _______cm.
12.如图所示,平行四边形ABCD中,BE⊥AD,CE平分∠BCD,AB=10,BC=16,则AE=__________.
三.解答题
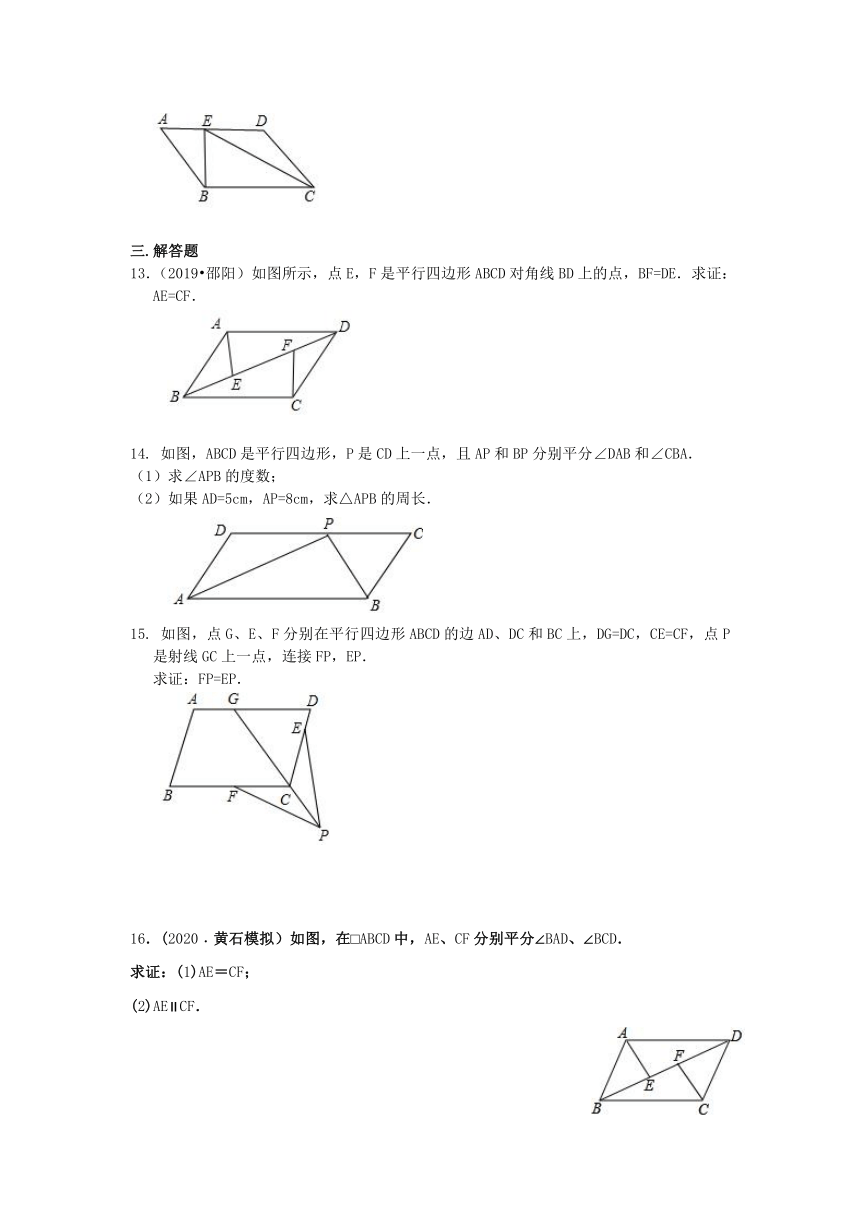
13.(2019?邵阳)如图所示,点E,F是平行四边形ABCD对角线BD上的点,BF=DE.求证:AE=CF.
14. 如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
(1)求∠APB的度数;
(2)如果AD=5cm,AP=8cm,求△APB的周长.
15. 如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP.
求证:FP=EP.
16.(2020﹒黄石模拟)如图,在□ABCD中,AE、CF分别平分∠BAD、∠BCD.
求证:(1)AE=CF;
(2)AE∥CF.
附加题:(2019春﹒沙坪坝区期中)如图,在□ABCD中,∠B=45°,过点C作CE⊥AD于点,连结AC,过点D作DF⊥AC于点F,交CE于点G,连结EF.
(1)若DG=8,求对角线AC的长;
(2)求证:AF+FG=.
【答案与解析】
一.选择题
1.【答案】C;
2.【答案】D;
3.【答案】C;
4.【答案】B;
【解析】解:AB不一定平行于PC,A不正确;
∵平行线间的距离处处相等,∴△ABC的面积等于△BCP的面积,B正确;
AC不一定等于BP,C不正确;
△ABC的周长不一定等于△BCP的周长,D不正确,
故选:B.
5.【答案】D;
【解析】设两条对角线的长为.所以,,所以选D.
6.【答案】B;
【解析】因为∠AFB=∠FBC,∠ABF=∠FBC,所以AF=AB=6;同理可证:DE=DC=6;EF=AF+DE-AD=2,即6+6-AD=2,解得AD=10.
二.填空题
7.【答案】48;
【解析】因为四边形ABCD是平行四边形,所以OD=OB,AD=BC=18cm.又因为△AOB的周长为54,所以OA+OB+AB=54,因为AB=24,所以OA+OB=54-24=30(),所以OA+OD=30(),所以OA+OD+AD=30+18=48().即△AOD的周长为48.
8.【答案】40;
【解析】过点A作AH⊥BC于H.在Rt△ABH中,∠B=30°,AB=8,
∴AH=AB=4().
∴BC·AH=10×4=40().
9.【答案】5,5;
【解析】由题意,∠DAC=∠BCA=30°,AB=BC=5,.
10.【答案】10;
【解析】解:∵AB=AC=5,∴∠B=∠C,
由DF∥AC,得∠FDB=∠C=∠B,
∴FD=FB,
同理,得DE=EC.
∴四边形AFDE的周长=AF+AE+FD+DE
=AF+FB+AE+EC
=AB+AC
=5+5=10.
故答案为10.
11.【答案】2;
【解析】∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵△AOD的周长=OA+OD+AD,△AOB的周长=OA+OB+AB,
又∵△AOD与△AOB的周长差是5,
∴AD=AB+5,
设AB=x,AD=5+x,
则2(x+5+x)=18,
解得x=2,
即AB=2.
故答案为2.
12.【答案】6;
【解析】∵平行四边形ABCD,
∴AD∥BC,AD=BC=16,AB=CD=10,
∴∠DEC=∠ECB,
∵CE平分∠DCB,
∴∠DCE=∠BCE,
∴∠DEC=∠DCE,
∴DE=DC=AB=10,
∴AE=16-10=6,
故答案为:6.
三.解答题
13.【解析】
证明:∵四边形ABCD为平行四边形,
∴BC=AD,BC∥AD,
∴∠EDA=∠FBC,
在△AED和△CFB中,
∴△AED≌△CFB(SAS),
∴AE=CF.
14.【解析】
解:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,
∴∠APB=180-(∠PAB+∠PBA)=90°;
(2)∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在RT△APB中,AB=10cm,AP=8,
∴BP==6(cm)
∴△APB的周长是6+8+10=24(cm).
15.【解析】
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DGC=∠GCB(两直线平行,内错角相等),
∵DG=DC,
∴∠DGC=∠DCG,
∴∠DCG=∠GCB,
∵∠DCG+∠DCP=180°,∠GCB+∠FCP=180°,
∴∠DCP=∠FCP,
∵在△PCF和△PCE中
,
∴△PCF≌△PCE(SAS),
∴PF=PE.
16. 【考点】全等三角形的判定与性质;平行四边形的性质.【专题】多边形与平行四边形;应用意识.【分析】(1)证明△ADE≌△CBF(ASA),可得AE=CF.
(2)利用全等三角形的性质证明∠AED=∠CFB即可.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠BAD=∠DCB,
∴∠ADE=∠CBF,
∵AE、CF分别平分∠BAD、∠BCD,
∴∠DAE==
∴∠DAE=∠BCF,
∴△ADE≌△CBF(ASA),
∴AE=CF.
(2)∵△ADE≌△CBF,
∴∠AED=∠CFB,
∴AE∥CF.
【点评】本题考查平行四边形的性质,全等三角形的判定和性质,平行线的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.
附加题:【考点】全等三角形的判定与性质;平行四边形的性质.平行四边形的性质解:
(1)∵在□ABCD中,∠B=45°,
∴∠ADC=∠B=45°,
∵CE⊥AD,
∴△CDE是等腰直角三角形,
∴CE=DE,∠DEC=∠AEC=90°,
∵DF⊥AC,
∴∠CFD=∠DEC=90°,
∴∠DGE=∠CGF,
∴∠EDG=∠ECA,
∴△DEG≌△CEA(ASA),
∴AC=DG=8;
(2)过E作EH⊥EF交DF于H,
∵∠FEH=∠DEC=90°,
∴∠DEH=∠CEF,
∵∠EDH=∠ECF,DE=CE,
∴△DEH≌△CEF(ASA),
∴EF=EH,DH=CF,
∴AC-CF=DG-DH,
即AF=HG,
∵FH=FG+GH=
∴AF+FG=.
【点评】本题考查了平行四边形的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质,正确的识别图形是解题的关键.
PAGE
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
